Bài toán thực tế lớp 10 Các số đặc trưng đo xu thế trung tâm
Bài toán thực tế lớp 10 Các số đặc trưng đo xu thế trung tâm có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều với bài tập đa dạng giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 10.
Bài toán thực tế lớp 10 Các số đặc trưng đo xu thế trung tâm
Chỉ từ 300k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 10 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
A. KIẾN THỨC CẦN NHỚ
1. Số trung bình
- Giả sử ta có một mẫu số liệu là .
Số trung bình (hay số trung bình cộng) của mẫu số liệu này, kí hiệu là , được tính bởi công thức .
- Giả sử mẫu số liệu được cho dưới dạng bảng tần số
Khi đó, công thức tính số trung bình trở thành , trong đó . Ta gọi n là cố mấu.
Chú ý: Kí hiệu là tần số tương đối (hay còn gọi là tần suất) của trong mẫu số liệu thì số trung bình còn có thể biểu diễn là .
-Ý nghĩa của số trung bình: Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đo xu thế trung tâm của mẫu đó.
2. Trung vị và tứ phân vị
Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được .
- Trung vị của mẫu, kí hiệu là , là giá trị ở chính giữa dãy . Cụ thể:
Nếu thì trung vị mẫu là .
Nếu thì trung vị mẫu là .
- Ý nghĩa của trung vị: Trung vị được dùng để đo xu thế trung tâm của mẫu số liệu. Trung vị là giá trị nằm ở chính giữa của mẫu số liệu theo nghĩa: luôn có ít nhất 50% số liệu trong mẫu lớn hơn hoặc bằng trung vị và ít nhất 50% số liệu trong mẫu nhỏ hơn hoặc bằng trung vị. Khi trong mẫu xuất hiện thêm một giá trị rất lớn hoặc rất nhỏ thì số trung bình sẽ bị thay đổi đáng kể nhưng trung vị thì ít thay đổi.
- Tứ phân vị của một mẫu ngẫu nhiên gồm 3 giá trị, đó là tứ phân vị thứ nhất, thứ hai và thứ ba (lần lượt kí hiệu là ). Ba giá trị này chia tập hợp dữ liệu đã sắp xếp thành bốn phần đều nhau. Cụ thể:
+ Giá trị tứ phân vị thứ hai, , chính là trung vị của mẫu.
+ Giá trị tứ phân vị thứ nhất, , là trung vị của nửa số liệu đã sắp xếp bên trái (không bao gồm nếu n lẻ).
+ Giá trị tứ phân vị thứ ba , là trung vị của nửa số liệu đã sắp xếp bên phải (không bao gồm nếu n lẻ).
- Ý nghĩa của tứ phân vị: Các điểm tứ phân vị chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần chứa khoảng 25% tổng số số liệu đã thu thập được. Tứ phân vị thứ nhất còn được gọi là tứ phân vị dưới và đại diện cho nửa mẫu số liệu phía dưới. Tứ phân vị thứ ba còn được gọi là tứ phân vị trên và đại diện cho nửa mẫu số liệu phía trên.
3. Mốt
- Cho một mẫu số liệu dưới dạng bảng tần số. Giá trị có tần số lớn nhất được gọi là mốt của mẫu số liệu, kí hiệu là .
- Ý nghĩa của mốt: Mốt đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.
Chú ý: Một mẫu số liệu có thể có nhiều mốt. Khi tất cả các giá trị trong mẫu số liệu có tần số xuất hiện bằng nhau thì mẫu số liệu đó không có mốt.
4. Khoảng biến thiên và khoảng tứ phân vị
Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được .
-Khoảng biến thiên của một mẫu số liệu, kí hiệu là R, là hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó, tức là: .
-Khoảng tứ phân vị, kí hiệu là , là hiệu giữa và , tức là .
- Ý nghĩa của khoảng biến thiên và khoảng tứ phân vị
+ Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu.
+ Khoảng tứ phân vị đặc trưng cho độ phân tán của một nửa các số liệu, có giá trị thuộc đoạn từ đến trong mẫu.
+ Khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu.
- Giá trị ngoại lệ
+ Khoảng tứ phân vị được dùng để xác định các giá trị ngoại lệ trong mẫu, đó là các giá trị quá nhỏ hay quá lớn so với đa số các giá trị của mẫu. Cụ thể, phần tử x trong mẫu là giá trị ngoại lệ nếu hoặc .
+ Khi mẫu có giá trị ngoại lệ, người ta thường sử dụng trung vị và khoảng tứ phân vị để đo mức độ tập trung và mức độ phân tán của đa số các phần tử trong mẫu số liệu.
5. Phương sai và độ lệch chuẩn
Giả sử ta có một mẫu số liệu là .
- Phương sai của mẫu số liệu này, kí hiệu là , được tính bởi công thức
trong đó là số trung bình của mẫu số liệu.
- Căn bậc hai của phương sai được gọi là độ lệch chuẩn, kí hiệu là S .
Giả sử mẫu số liệu được cho dưới dạng bảng tần số
- Khi đó, công thức tính phương sai trở thành
trong đó .
- Có thể biến đổi công thức tính phương sai trên thành
- Ý nghĩa của phương sai và độ lệch chuẩn
+ Phương sai là trung bình cộng của các bình phương độ lệch từ mỗi giá trị của mẫu số liệu đến số trung bình.
+ Phương sai và độ lệch chuẩn được dùng để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình. Phương sai và độ lệch chuẩn càng lớn thì các giá trị của mẫu càng cách xa nhau (có độ phân tán lớn).
B. BÀI TẬP VẬN DỤNG
Câu 1: Chiều cao (đơn vị: xăng-ti-mét) của các bạn tổ lở lớp 10A lần lượt là:
Đối với mẫu số liệu trên, hãy tìm:
a. Số trung bình cộng;
b. Trung vi:
c. Mốt;
d. Tứ phân vi.
Lời giải
Sắp xếp số liệu theo thứ tự không giảm là:
a.
b. Mẫu số liệu trên có 9 số, vậy
c. Trung vị của mẫu số liệu là:
Trung vị của dãy 155155158159 là
Trung vị của dãy 165165167171 là
d. và
Câu 2: Số đôi giày bán ra trong Quý IV năm 2020 của một cửa hàng được thống kê trong bảng tần số sau:
|
Cỡ giày |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
Tẩn số |
40 |
48 |
52 |
70 |
54 |
47 |
28 |
3 |
|
(Số đôi giày bán được) |
|
|
|
|
|
|
|
|
a. Mốt của mẫu số liệu trên là bao nhiêu?
b. Cửa hàng đó nên nhập về nhiều hơn cỡ giày nào để bán trong tháng tiếp theo?
Lời giải
a.
b. Cửa hàng đó nên nhập về nhiều hơn cỡ giày 40 để bán trong tháng tiếp theo.
Câu 3: Bảng 2 cho biết nhiệt độ trung bình các tháng trong năm ở Hà Nội.
a. Nhiệt độ trung bình trong năm ở Hà Nội là bao nhiêu?
b. Nhiệt độ trung bình của tháng có giá trị thấp nhất là bao nhiêu độ C? Cao nhất là bao nhiêu độ C?
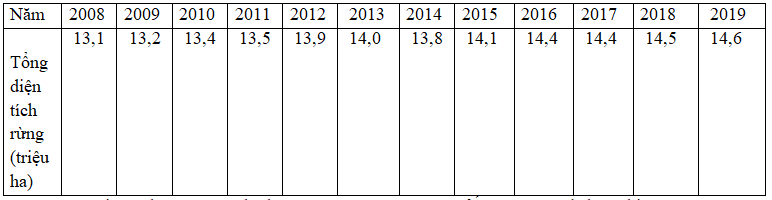
Câu 4: Bảng 3 cho biết tổng diện tích rừng từ năm 2008 đến năm 2019 ở nước ta.
a. Diện tích rừng trung bình của nước ta từ năm 2008 đến năm 2019 là bao nhiêu?
b. Từ năm 2008 đến năm 2019, diện tích rừng của năm có giá trị thấp nhất là bao nhiêu triệu héc-ta? Cao nhất là bao nhiêu triệu héc-ta?
c. So với năm 2008, tỉ lệ tổng diện tích rừng của nước ta năm 2019 tăng lên được bao nhiêu phần trăm? Theo em, tỉ lệ tăng đó là cao hay thấp?
d. Hãy tìm hiểu số liệu về tổng diện tích rừng của tỉnh em đang sống trong một số năm gần đây.
Câu 5: Bốn bạn Bình, Cường, Hoa, Kiên cùng thi vào trường phổ thông chất lượng cao Bình Minh. Kết quả thi được cho bởi bảng thống kê sau:
|
Học sinh |
Điểm Toán |
Điểm Ngũ Văn |
Điểm Tiếng Anh |
|
Bình |
10 |
8 |
9 |
|
Cường |
6 |
7 |
5 |
|
Hoa |
10 |
10 |
4 |
|
Kiên |
9 |
5 |
10 |
Tính điểm trung bình kết quả thi 3 môn Toán, Ngũ̃ Văn, Tiếng Anh của mỗi bạn và cho biết bạn nào trúng tuyển. Biết rằng, nếu muốn trúng tuyển, điểm trung bình các môn thi ở trên phải lớn hơn hoặc bằng 8 và không môn nào dưới 5 điểm.
Câu 6: Đầu năm học, nhà trường cho học sinh khám sức khỏe. Mẫu số liệu thống kê kết quả đo cân nặng (đơn vị: ki-lô-gam) của 7 bạn nam đầu tiên như sau:
Trung vị của mẫu số liệu trên là bao nhiêu?
Câu 7: Mẫu số liệu thống kê chiều cao (đơn vị: xăng-ti-mét) của 10 bạn tổ I lớp 10A như sau:
Trung vị của mẫu số liệu trên là bao nhiêu?
................................
................................
................................
Xem thêm Chuyên đề Toán thực tế lớp 10 chương trình mới có lời giải hay khác:
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều


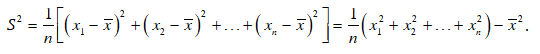
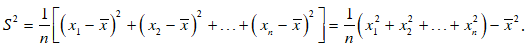




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

