Bài toán thực tế lớp 10 Đại số tổ hợp

Bài toán thực tế lớp 10 Đại số tổ hợp có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều với bài tập đa dạng giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 10.

Bài toán thực tế lớp 10 Đại số tổ hợp

Xem thử

Chỉ từ 300k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 10 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

A – KIẾN THỨC CẦN NHỚ

Có hai quy tắc đếm quan trọng nhất, đó là quy tắc cộng và quy tắc nhân.

1. Quy tắc cộng. Giả sử có một công việc có thể được thực hiện theo một trong k phương án khác nhau:

- Phương án 1 có $n_1$ cách thực hiện;

- Phương án 2 có $n_2$ cách thực hiện;

….

- Phương án k có $n_k$ cách thực hiện.

Khi đó số cách thực hiện công việc là $n_1+n_2+\dots +n_k$ cách.

2. Quy tắc nhân. Giả sử có một công việc nào đó phải hoàn thành qua k công đoạn liên tiếp nhau:

- Công đoạn 1 có $m_1$ cách thực hiện;

- Công đoạn 2 có $m_2$ cách thực hiện;

….

- Công đoạn k có $m_k$ cách thực hiện.

Khi đó số cách thực hiện công việc là $m_1\cdot m_2\cdot \dots \cdot m_k$ cách.

Trong các bài toán đếm, các khái niệm cơ bản nhất là hoán vị, tổ hợp và chỉnh hợp.

3. Hoán vị. Một hoán vị của một tập hợp n phần tử là một cách sắp xếp có thứ tự n phần tử đó $(n\in \mathbb{N},n\ge 1)$. Số các hoán vị của n, kí hiệu là $P_n$, được tính bằng công thức: $P_n=n!=n\cdot (n-1)\cdot (n-2)\dots 2\cdot 1.$

Ta quy ước $0!=1$.

4. Chỉnh hợp. Một chỉnh hợp chập k của n là một cách sắp xếp có thứ tự k phần tử từ một tập hợp n phần tử, với $k,n\in \mathbb{N},1\le k\le n$. Số các chỉnh hợp chập k của n, kí hiệu là $A_n^k$ được tính bằng công thức:

$A_n^k=n\cdot (n-1)\cdot (n-2)\dots (n-k+1),$ hay $A_n^k=\frac{n!}{(n-k)!}.$

5. Tổ hợp. Một tổ hợp chập k của n là một cách chọn k phần tử từ một tập hợp n phần tử, với $k,n\in \mathbb{N},0\le k\le n$. Số các tổ hợp chập k của n, kí hiệu là $C_n^k$, được tính bằng công thức: $C_n^k=\frac{n!}{(n-k)!\cdot k!}.$

Để tránh nhầm lẫn các khái niệm tổ hợp và chỉnh hợp, cần lưu ý rằng chỉnh hợp liên quan đến việc chọn có xếp thứ tự còn tổ hợp là chọn không xếp thứ tự.

B – BÀI TẬP VẬN DỤNG

BÀI TOÁN 1: QUY TẮC CỘNG- QUY TẮC NHÂN

Câu 1: Trong một trường trung học phổ thông, khối 10 có 245 học sinh nam và 235 học sinh nữ.

a. Nhà trường cần chọn một học sinh ở khối 10 đi dự buổi giao lưu với học sinh các trường trung học phổ thông trong tỉnh. Hỏi nhà trường có bao nhiêu cách chọn?

b. Nhà trường cần chọn hai học sinh ở khối 10, trong đó có 1 nam và 1 nữ, đi dự trại hè của học sinh trong tình. Hỏi nhà trường có bao nhiêu cách chọn?

Lời giải

a.

- Chọn học sinh nam: Có 245 cách

- Chọn học sinh nứ: Có 235 cách

Vậy nhà trường có 245 + 235 = 480 cách chọn một học sinh

b.

- Chọn học sinh nam: Có 245 cách

- Chọn học sinh nữ: Có 235 cách

Vậy nhà trường có 245.235 = 57575 cách chọn hai học sinh 1 nam và 1 nữ.

Câu 2: Trong giải thi đấu bóng đá World Cup, vòng bảng có 32 đội tham gia, được chia làm 8 bảng, mỗi bảng có 4 đội đấu vòng tròn một lượt. Tính số trận được thi đấu trong vòng bảng theo thể thức trên.

Lời giải

Mỗi bảng có số trận đấu là:

3 + 2 + 1 = 6 (trận)

Tổng số trận được thi đấu trong vòng bảng là:

8 . 6 = 48 (trận)

Câu 3: Ở Canada, mã bưu chính có 6 kí tự gồm: 3 chữ cái in hoa (trong số 26 chữ cái tiếng Anh) và 3 chữ số. Mỗi mã bưu chính bắt đầu bằng 1 chữ cái và xen kẽ bằng 1 chữ số. (Nguồn: https://capath.vn/postal-code-canada)

a. Có thể tạo được bao nhiêu mã bưu chính?

b. Có thể tạo được bao nhiêu mã bắt đầu bằng chữ S?

c. Có thể tạo được bao nhiêu mã bắt đầu bằng chữ S và kết thúc bằng chữ số 8?

Câu 4: Một hãng thời trang đưa ra một mẫu áo sơ mi mới có ba màu: trắng, xanh, đen. Mỗi loại có các cỡ $S,M,L,XL,XXL$.

a. Vẽ sơ đồ hình cây biểu thị các loại áo sơ mi với màu và cỡ áo nói trên.

b. Nếu một cửa hàng muốn mua tất cả các loại áo sơ mi (đủ loại màu và đủ loại cỡ áo) và mỗi loại một chiếc để về giới thiệu thì cần mua tất cả bao nhiêu chiếc áo sơ mi?

Câu 5: Một khách sạn nhỏ chuẩn bị bữa ăn sáng gồm 2 đồ uống là: trà và cà phê; 3 món ăn là: phở, bún và cháo; 2 món tráng miệng là: bánh ngọt và sữa chua.

a. Vẽ sơ đồ hình cây biểu thị các cách chọn khẩu phần ăn gồm đủ ba loại: đồ uống, món ăn và món tráng miệng.

b. Tính số cách chọn khẩu phần ăn gồm: 1 đồ uống, 1 món ăn và 1 món tráng miệng.

Câu 6: Cho kiểu gen AaBbDdEe. Giả sử quá trình giảm phân tạo giao tử bình thường, không xảy ra đột biến.

a. Vẽ sơ đồ hình cây biểu thị sự hình thành giao tử.

b. Từ đó, tính số loại giao tử của kiểu gen $AaBbDdEe$.

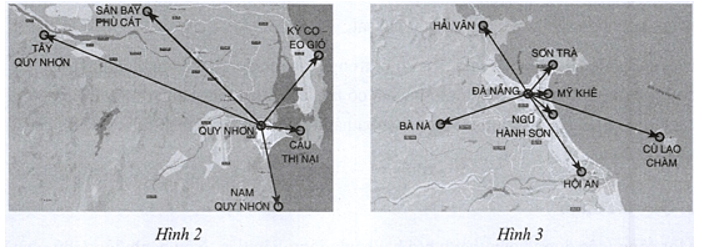
Câu 7: Gia đình bạn Dương dự định chọn một địa điểm du lịch ở Quy Nhơn (Bình Định) hoặc Đà Nẵng. Nếu chọn Quy Nhơn thì có 5 địa điểm tham quan (Hình 2), nếu chọn Đà Nã̃ng thì có 7 địa điểm tham quan (Hình 3). Hỏi gia đình bạn Dương có bao nhiêu cách để chọn một địa điểm tham quan?

................................

................................

................................

Xem thử

Xem thêm Chuyên đề Toán thực tế lớp 10 chương trình mới có lời giải hay khác:

• Bài toán thực tế lớp 10 Hai phương trình quy về phương trình bậc hai

• Bài toán thực tế lớp 10 Các số đặc trưng đo xu thế trung tâm

• Bài toán thực tế lớp 10 Đường thẳng

• Bài toán thực tế lớp 10 Phương trình đường tròn

• Bài toán thực tế lớp 10 Ba đường Conic

• Bài toán thực tế lớp 10 Xác suất

---