Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác lớp 7 (Lý thuyết Toán 7 Kết nối tri thức)
Với tóm tắt lý thuyết Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác lớp 7 (Lý thuyết Toán 7 Kết nối tri thức)
(199k) Xem Khóa học Toán 7 KNTT
Bài giảng: Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác - Cô Trần Thị Den Ni (Giáo viên VietJack)
Lý thuyết Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
1. Hai tam giác bằng nhau
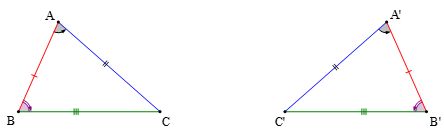
• Hai tam giác ABC và A'B'C'bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, nghĩa là:
AB=A'B'; AC=A'C'; BC=B'C' và ; ; .
• Khi kí hiệu hai tam giác bằng nhau thì thứ tự các đỉnh tương ứng phải được viết theo cùng 1 thứ tự.
Ở đây hai đỉnh A và A' (B và B', C và C') là hai đỉnh tương ứng;
Hai góc A và A' (B và B', C và C') là hai góc tương ứng;
Hai cạnh AB và A'B' (AC và A'C', BC và B'C') là hai cạnh tương ứng.
Khi đó ta kí hiệu:
Ví dụ:
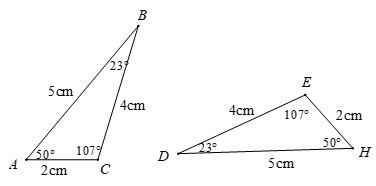
+ Cho hai tam giác trong hình dưới đây, ta thấy:
; ; (các góc tương ứng)
AB = DH = 5 cm; BC = DE = 4cm; AC = EH = 2cm (các cạnh tương ứng)
Do đó hai tam giác trên bằng nhau. Kí hiệu theo thứ tự tương ứng là:
2. Trường hợp bằng nhau thứ nhất của tam giác: Cạnh – cạnh – cạnh (c.c.c)
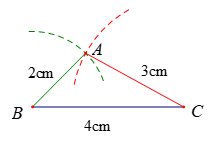
• Cách vẽ tam giác khi biết số đo ba cạnh.
Chẳng hạn: Vẽ tam giác ABC biết AB = 2 cm; AC = 3 cm; BC = 4 cm.
+ Dùng thước kẻ có vạch chia vẽ đoạn BC = 4 cm (hoặc có thể vẽ AB hoặc AC trước)
+ Dùng compa mở khẩu độ 2 cm, tâm tại điểm B, vẽ 1 cung tròn; mở compa khẩu độ 3 cm, tâm tại điểm C, vẽ một cung tròn. Giao điểm của 2 cung tròn là điểm A.
+ Vẽ các đoạn thẳng AB; AC ta được tam giác ABC.
• Trường hợp bằng nhau cạnh - cạnh - cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
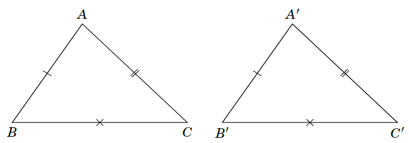
+ Cho tam giác ABC và tam giác trong hình dưới đây:
Ta có: AB = ; AC = A'C'; BC = B'C'
Khi đó:
Chú ý:
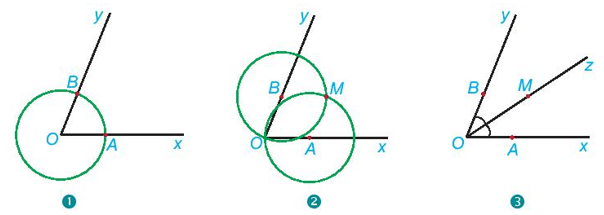
• Cách vẽ tia phân giác của một góc dựa và thước kẻ và compa.
Vẽ tia phân giác của góc xOy ta làm như sau:
1) Vẽ đường tròn tâm O cắt Ox, Oy lần lượt tại A và B.
2) Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn này cắt nhau tại điểm M khác điểm O.
3) Vẽ tia Oz đi qua M. Tia Oz là tia phân giác của góc xOy.
Bài tập Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
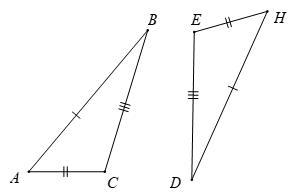
Bài 1. Cho tam giác ABC và DEH trong hình dưới đây.
Xác định trong các khẳng định sau, khẳng định nào đúng?
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải
Hai tam giác ABC và HDE có:
AB = HD
BC = DE
AC = HE
Vậy (c.c.c)
Khi đó A và H (B và D; C và E) là hai đỉnh tương ứng
a)
Các đỉnh tương ứng không viết cùng thứ tự nên khẳng định sai.
b)
Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.
c)
Đỉnh A và H; đỉnh C và E không được viết cùng thứ tự nên khẳng định sai.
d)
Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.
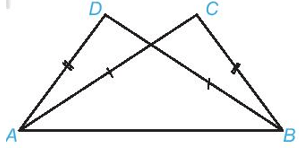
Bài 2. Cho hình vẽ dưới đây, biết AD = BC, AC = BD. Chứng minh rằng .
Hướng dẫn giải
Hai tam giác ADB và BCA có:
AD = BC (theo giả thiết)
BD = AC (theo giả thiết)
AB là cạnh chung
Vậy (c.c.c)
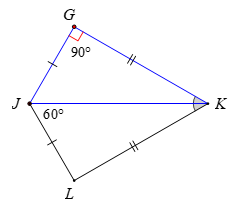
Bài 3. Cho hình vẽ dưới đây, biết JG = JL, GK = LK, , .
a) Chứng minh rằng
b) Tính góc GKL.
Hướng dẫn giải
a) Xét hai tam giác JGK và JLK có:
JG = JL (theo giả thiết)
GK = LK (theo giả thiết)
JK là cạnh chung
Vậy (c.c.c)
b) Vì (theo câu a)
⇒ (hai góc tương ứng)
⇒
Xét tam giác JGK có: (tổng 3 góc trong tam giác)
⇒
⇒
Vì (theo câu a)
⇒ (hai góc tương ứng)
⇒
Vậy
Học tốt Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Các bài học để học tốt Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Toán lớp 7 hay khác:
Giải sgk Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Giải sbt Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
(199k) Xem Khóa học Toán 7 KNTT
Xem thêm tóm tắt lý thuyết Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Lý thuyết Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
Lý thuyết Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Xem thêm các tài liệu học tốt lớp 7 hay khác:
- Giải sgk Toán 7 Kết nối tri thức
- Giải SBT Toán 7 Kết nối tri thức
- Giải lớp 7 Kết nối tri thức (các môn học)
- Giải lớp 7 Chân trời sáng tạo (các môn học)
- Giải lớp 7 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giải bài tập Toán lớp 7 của chúng tôi được biên soạn bám sát sgk Toán 7 Tập 1 & Tập 2 bộ sách Kết nối tri thức với cuộc sống (NXB Giáo dục).
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 7 (hay nhất) - KNTT
- Soạn văn 7 (ngắn nhất) - KNTT
- Giải sgk Toán 7 - KNTT
- Giải Tiếng Anh 7 Global Success
- Giải Tiếng Anh 7 Friends plus
- Giải sgk Tiếng Anh 7 Smart World
- Giải Tiếng Anh 7 Explore English
- Giải sgk Khoa học tự nhiên 7 - KNTT
- Giải sgk Lịch Sử 7 - KNTT
- Giải sgk Địa Lí 7 - KNTT
- Giải sgk Giáo dục công dân 7 - KNTT
- Giải sgk Tin học 7 - KNTT
- Giải sgk Công nghệ 7 - KNTT
- Giải sgk Hoạt động trải nghiệm 7 - KNTT
- Giải sgk Âm nhạc 7 - KNTT


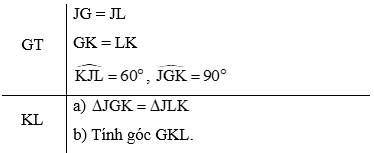



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

