Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

HOT Sale 40% sách Toán - Văn - Anh 8 ngày 25-10 trên Shopee mall

Tổng hợp lý thuyết Toán 8 Chương 6: Một số yếu tố thống kê và xác suất sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

(199k) Xem Khóa học Toán 8 CD

Quảng cáo

Lý thuyết Tổng hợp Lý thuyết Toán 8 Chương 6

1. Thu thập dữ liệu

Có nhiều cách để thu thập dữ liệu, chẳng hạn: quan sát, lập phiếu điều tra (phiếu hỏi), tiến hành phỏng vấn,... hoặc thu thập về những nguồn có sẵn như sách, báo, trang web, các phương tiện thông tin đại chúng,...

2. Phân loại và tổ chức dữ liệu

• Trong các dữ liệu thu thập được:

− Có những dữ liệu thống kê là số (số liệu), những dữ liệu này còn gọi là dữ liệu định lượng.

− Có những dữ liệu thống kê không phải là số, những dữ liệu này còn gọi là dữ liệu định tính.

• Do dữ liệu thu thập được thường rất đa dạng và phong phú nên để thuận tiện trong mô tả, biểu diễn và xử lí ta có thể phân chia, sắp xếp các dữ liệu đó thành những loại dữ liệu theo những tiêu chí cho trước.

• Việc sắp xếp thông tin theo những tiêu chí nhất định gọi là phân loại dữ liệu.

• Dựa trên tiêu chí định tính và định lượng, ta có thể phân loại các dữ liệu thành hai loại:

Quảng cáo

− Dữ liệu định lượng được biểu diễn bằng số thực;

− Dữ liệu định tính được biểu diễn bằng từ, chữ cái, kí hiệu, ...

• Để thuận tiện trong tổ chức dữ liệu thu nhập được, ta có thể phân nhóm mỗi loại dữ liệu đó thành các nhóm theo những tiêu chí cho trước.

Nhận xét: Việc phân loại dữ liệu thống kê phụ thuộc vào những tiêu chí đưa ra, hay nói cách khác, phụ thuộc vào mục đích phân loại.

3. Tính hợp lí của dữ liệu

Sau khi thu thập, phân loại và tổ chức dữ liệu, ta cần xem xét tính hợp lí của những dữ liệu thống kê đó, đặc biệt chỉ ra những dữ liệu không hợp lí.

Nhận xét: Để đánh giá tính hợp lí của dữ liệu, ta cần đưa ra các tiêu chí đánh giá, chẳng hạn như dữ liệu phải:

− Đúng định dạng;

− Nằm trong phạm vi dự kiến;

− Phải có tính đại diện đối với vấn đề thống kê.

Để đánh giá tính hợp lí của dữ liệu, ta có thể dựa vào mối liên hệ toán học đơn giản giữa các số liệu.

Quảng cáo

Chẳng hạn, để đảm bảo tính hợp lí, dữ liệu cần phải đáp ứng đúng các tiêu chí toán học đơn giản như:

− Tổng tất cả các số liệu thành phần bằng số liệu của toàn thể;

− Số lượng của bộ phận phải nhỏ hơn số lượng của toàn thể.

5. Biểu diễn dữ liệu trên các bảng và biểu đồ thống kê

Nhận xét:

− Để biểu diễn dữ liệu thống kê, ta cần lựa chọn bảng, biểu đồ thích hợp.

− Để có thể hoàn thiện được biểu đồ (hoặc bảng thống kê) đã lựa chọn, ta cần biểu diễn được dữ liệu vào biểu đồ (hoặc bảng) đó. Muốn vậy, ta cần biết cách xác định mỗi yếu tố của biểu đồ (hoặc bảng) thống kê đó.

6. Biểu diễn khác nhau theo những cách khác nhau

Nhận xét: Đối với một tập dữ liệu, ta có thể:

– Biểu diễn dữ liệu đó theo những cách khác nhau vào bảng, biểu đồ thích hợp.

– Chuyển tập dữ liệu đó từ dạng biểu diễn này sang dạng biểu diễn khác.

7. Phát hiện vấn đề dựa trên phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ

Quảng cáo

Để phát hiện vấn đề (hoặc quy luật đơn giản) dựa trên phân tích và xử lí số liệu thu được, ta cần:

– Nhận biết được mối liên hệ toán học đơn giản giữa các số liệu đã được biểu diễn;

– Thực hiện được tính toán và suy luận toán học.

8. Giải quyết những vấn đề đơn giản dựa trên phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ

Để giải quyết vấn đề đã được thực hiện (dựa trên phân tích và xử lí số liệu thu được), ta cần thực hiện những tính toán và suy luận trên cơ sở mối liên hệ toán học giữa các số liệu đó.

9. Xác suất của biến cố trong trò chơi tung đồng xu

Trong trò chơi tung đồng xu, ta quy ước đồng xu là cân đối đồng chất.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

Tung đồng xu 1 lần.

• Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt N” bằng $\frac{1}{2};$

• Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt S” bằng $\frac{1}{2} .$

10. Xác suất của biến cố trong trò chơi vòng quay số

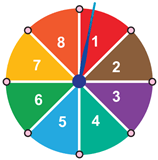
Một đĩa tròn bằng bìa cứng được chia làm tám phần bằng và ghi số 1; 2; 3; 4; 5; 6; 7; 8, chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

Quay đĩa tròn 1 lần.

Nếu k là số kết quả thuận lợi cho một biến cố thì xác suất của biến cố đó bằng $\frac{k}{8} .$

11. Xác suất của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng

Ta xét trò chơi chọn ngẫu nhiên một đối tượng từ nhóm đối tượng với số kết quả có thể xảy ra là hữu hạn và khả năng xảy ra của từng kết quả là giống nhau.

Xác suất của một biến cố bằng tỉ bằng tỉ số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.

12. Xác suất thực nghiệm của một biến cố trong trò chơi tung đồng xu

12.1. Khái niệm

Trong trò chơi tung đồng xu, ta quy ước đồng xu là cân đối đồng chất.

• Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” khi tung đồng xu nhiều lần bằng

• Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” khi tung đồng xu nhiều lần bằng

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

12.2. Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Trong trò chơi tung đồng xu, khi số lần tung ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” (hoặc biến cố “Mặt xuất hiện của đồng xu là mặt S”) ngày càng gần với xác suất với xác suất của biến cố đó.

13. Xác suất thực nghiệm của một biến cố trong trò chơi gieo xúc xắc

13.1. Khái niệm

Trong trò chơi gieo xúc xắc, ta quy ước xúc xắc là cân đối đồng chất. Mỗi xúc xắc có sáu mặt, số chấm ở mỗi mặt là một trong các số 1, 2, 3, 4, 5, 6.

• Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt k chấm” (k ∈ ℕ, 1 ≤ k ≤ 6) khi gieo xúc xắc nhiều lần bằng

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

13.2. Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Tương tự như trò chơi đồng xu.

Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của biến cố ngày càng gần với xác suất với xác suất của biến cố đó.

14. Xác suất thực nghiệm của một biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng

14.1. Khái niệm

Từ một nhóm k đối tượng sao cho khả năng được chọn ra của k đối tượng đó là như nhau. Xét một đối tượng A trong nhóm đối tượng đó. Mỗi lần ta chọn ngẫu nhiên một đối tượng trong nhóm, ghi lại tên của đối tượng được chọn ra và bỏ lại đối tượng đó vào nhóm.

Xác suất thực nghiệm của biến cố “Đối tượng A được chọn ra” khi chọn đối tượng nhiều lần bằng

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

14.2. Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng, mỗi lần ta lấy ngẫu nhiên một đối tượng, ghi lại đối tượng lấy ra và bỏ lại đối tượng đó vào nhóm đối tượng đã cho.

Tương tự như trò chơi tung đồng xu.

Trong trò chơi tung đồng xu, khi số lần lấy ra ngẫu nhiên ngày càng lớn thì xác suất thực nghiệm của biến cố “Đối tượng lấy ra là đối tượng A” ngày càng gần với xác suất với xác suất của biến cố đó.

Bài tập Tổng hợp Lý thuyết Toán 8 Chương 6

Bài 1. Đề xuất phương pháp thu thập dữ liệu cho các vấn đề sau:

a) So sánh tổng số huy chương vàng nhận được ở SEA Games 32 của Việt Nam và Thái Lan.

b) Số học sinh đạt điểm 8 trở lên môn Ngữ Văn của học sinh lớp 7A.

c) Mức độ hài lòng của người dân khi sử dụng nền tảng mạng xã hội Facebook.

d) Tổng số học sinh Giỏi của một trường Trung học cơ sở.

Hướng dẫn giải

Dữ liệu	Phương pháp thu thập
a)	Thu thập từ nguồn có sẵn như sách, báo, Internet, …
b)	Lập phiếu khảo sát, phỏng vấn các học sinh trong lớp
c)	Phỏng vấn, lập phiếu khảo sát
d)	Thu thập từ nguồn có sẵn như báo, Internet,… hoặc phỏng vấn, lập phiếu khảo sát

Bài 2. Cho các dữ liệu sau:

• Các môn thể thao yêu thích của lớp 7A: Đá bóng, bóng rổ, cầu lông, bơi;

• Đánh giá của các bạn học sinh về chất lượng bài giảng: Tốt, Xuất sắc, Khá, Trung bình;

• Cân nặng (đơn vị kilôgam) của 5 bạn trong lớp: 43, 42, 45, 48, 50;

• Tên một số môn học của khối 7: Toán, Ngữ văn, Địa lí, …

• Màu sắc khi chín của một số loại trái cây: vàng, cam, đỏ, …;

• Điểm trung bình môn Toán của một số bạn học sinh: 5,5; 6,5, 7,8; …

Tìm dữ liệu định tính và dữ liệu định lượng trong các dữ liệu trên.

Hướng dẫn giải

Các môn thể thao yêu thích của lớp 7A; Đánh giá của các bạn học sinh về chất lượng bài giảng; Tên một số môn học của khối 7; Màu sắc khi chín của một số loại trái cây là các dữ liệu định tính.

Cân nặng (đơn vị kilôgam) của 5 bạn trong lớp; Điểm trung bình môn Toán của một số bạn học sinh là các dữ liệu định lượng.

Bài 3. Để tìm hiểu về các động vật có xương sống trên Trái Đất, bạn Loan đã sưu tầm tư liệu về những động vật sau: cá rô đồng, cá chép, cá thu, ếch, nhái, cóc, rắn hổ mang, thằn lằn, cá sấu, gà Đông Tảo, chim bồ câu, chim ưng, trâu, mèo, sư tử. Em hãy giúp bạn Loan phân nhóm các động vật đó theo những tiêu chí sau: Cá; Lưỡng cư; Bò sát; Chim; Động vật có vú.

Hướng dẫn giải

Ta phân nhóm theo các tiêu chí sau:

• Nhóm 1 (Cá): Cá rô đồng, cá chép, cá thu;

• Nhóm 2 (Lưỡng cư): Ếch, nhái, cóc, cá sấu;

• Nhóm 3 (Bò sát): rắn hổ mang, thằn lằn;

• Nhóm 4 (Chim): Chim bồ câu, chim ưng;

• Nhóm 5 (Động vật có vú): trâu, mèo, sư tử.

Bài 4. Bạn Nga đã sưu tầm tên những loại cây.

Kết quả sưu tầm được như sau: Bồ công anh; Cây sầu riêng; Cây cam; Cỏ mần trầu; Cây nhọ nồi; Cây roi; Cây ngải cứu.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

a) Bạn Nga sưu tầm được bao nhiêu cây?

b) Hãy sắp xếp các loại cây mà bạn Nga đã sưu tầm theo những nhóm sau:

Nhóm 1. Các loại cây ăn quả.

Nhóm 2. Các loại cây thuốc dùng để trị bệnh.

Hướng dẫn giải

a) Bạn Nga sưu tầm được bao nhiêu 7 loại cây.

b) Sắp xếp các loại cây mà bạn Nga đã sưu tầm theo những nhóm:

Nhóm 1. Các loại cây ăn quả: Cây cam; cây sầu riêng; Cây roi.

Nhóm 2. Các loại cây thuốc dùng để trị bệnh: Cây ngải cứu; cây mần trầu; cây bò công anh; cây nhọ nồi.

Bài 5. Xét tính hợp lí của bảng thống kê sau:

Thống kê số huy chương bạc bạn Nam đạt được trong kỳ thi thể thao của trường
Môn thể thao	Số huy chương bạc
Đá cầu	1
Bơi	0
Cầu lông	0,5
Điền kinh	Hoàn thành

Hướng dẫn giải

Dữ liệu: Số huy chương bạc “Hoàn thành” không đúng định dạng (dữ liệu phải là số).

Số liệu 0,5không hợp lí vì số huy chương bạc phải là số tự nhiên.

Bài 6. Bảng số liệu dưới đây cho biết số lượng các loại hoa được trồng trong một khu vườn.

Loại hoa	Số cây
Hoa hồng	100
Hoa cúc	120
Hoa lay ơn	90
Hoa thược dược	115

Hãy lựa chọn loại biểu đồ thích hợp để biểu diễn dữ liệu từ bảng thống kê trên và vẽ biểu đồ đó.

Hướng dẫn giải

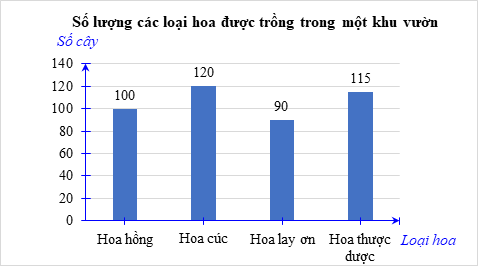
Ta có thể dùng biểu đồ cột hoặc biểu đồ đoạn thẳng để biểu diễn dữ liệu trên.

– Biểu đồ cột:

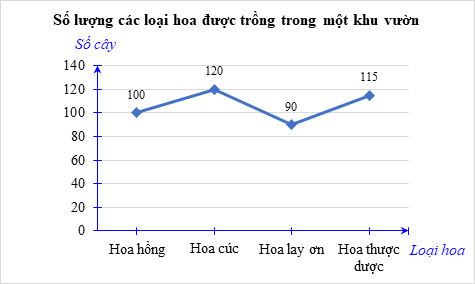
Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

– Biểu đồ đoạn thẳng:

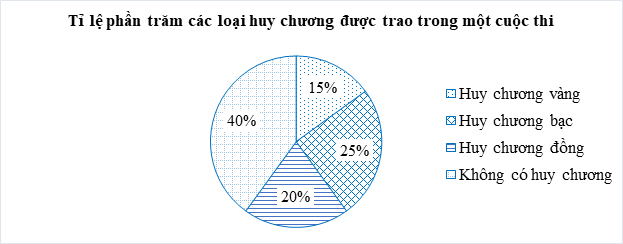
Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

Bài 7. Cho biểu đồ biểu diễn tỉ lệ phần trăm của các loại huy chương được trao trong một cuộc thi.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

Chuyển dữ liệu từ hình trên sang dạng bảng thống kê theo mẫu sau:

Loại huy chương	Huy chương vàng	Huy chương bạc	Huy chương đồng	Không có huy chương
Tỷ lệ phần trăm	?	?	?	?

Hướng dẫn giải

Chuyển dữ liệu trong hình sang dạng bảng thống kê ta có:

Loại huy chương	Huy chương vàng	Huy chương bạc	Huy chương đồng	Không có huy chương
Tỷ lệ phần trăm	15%	25%	20%	40%

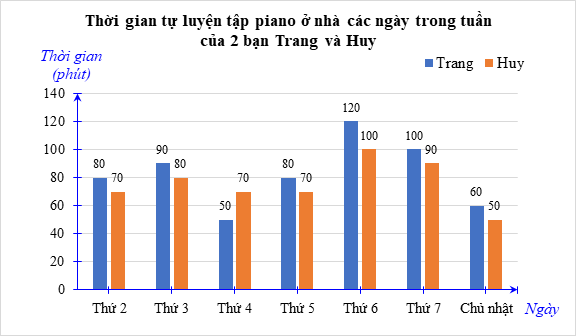
Bài 8. Thời gian tự luyện tập piano ở nhà các ngày trong tuần của 2 bạn Trang và Huy cho bởi bảng dưới đây.

Thời gian (phút)	Thứ 2	Thứ 3	Thứ 4	Thứ 5	Thứ 6	Thứ 7	Chủ nhật
Trang	80	90	50	80	120	100	60
Huy	70	80	70	70	100	90	50

Lựa chọn dạng biểu đồ thích hợp để biểu diễn bảng thống kê trên,sau đó trả lời các câu hỏi sau:

a) Tính tổng thời gian luyện tập piano ở nhà trong cả tuần của bạn Trang.

b) Tính số phần trăm giữa tổng thời gian luyện tập piano ở nhà tổng cả tuần của bạn Huy và tổng thời gian trong một tuần.

Hướng dẫn giải

Ta sử dụng biểu đồ cột kép để biểu diễn dữ liệu của bảng thống kê đã cho.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

a) Nhìn vào bảng thống kê ta thấy, thời gian tự luyện tập piano của bạn Trang các ngày Thứ 2, Thứ 3, Thứ 4, Thứ 5, Thứ 6, Thứ 7, Chủ nhật lần lượt là 80, 90, 50, 80, 120, 100, 60 (phút).

Từ đó ta có tổng thời gian tự luyện tập piano ở nhà các ngày trong tuần của bạn Trang là:

80 + 90 + 50 + 80 + 120 + 100 + 60 = 580 (phút).

Vậy tổng thời gian tự luyện tập piano ở nhà các ngày trong tuần của bạn trang là 580 phút.

b) Thời gian tự luyện tập piano của bạn Huy các ngày Thứ 2, Thứ 3, Thứ 4, Thứ 5, Thứ 6, Thứ 7, Chủ nhật lần lượt là 70, 80, 70, 70, 100, 90, 50 (phút).

Từ đó ta có tổng thời gian tự luyện tập piano ở nhà các ngày trong tuần của bạn Huy là:

70 + 80 + 70 + 70 + 100 + 90 + 50 = 530 (phút).

1 ngày có 24 giờ, 1 tuần có 7 ngày.

Do đó, tổng thời gian của 1 tuần là: 24.7 = 168 giờ = 10 080 (phút).

Vậy tỉ số phần trăm giữa tổng thời gian luyện tập piano ở nhà tổng cả tuần của bạn Huy và tổng thời gian trong một tuần là: $\frac{530}{10 080} .100 % \approx 5, 26 % .$

Bài 9. Chi tiêu 1 tháng của gia đình bạn Nam được liệt kê bởi bảng dữ liệu sau:

Chi tiêu

Học hành

Ăn uống

Mua sắm

Đi lại

Chi phí khác

Tiết kiệm

Số tiền

(triệu đồng)

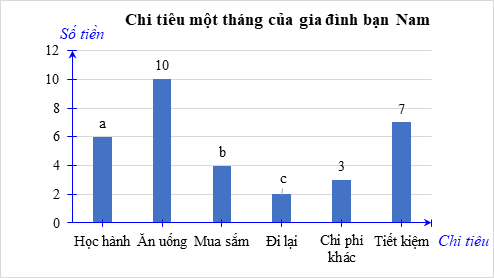
a) Số liệu từ bảng thống kê được biểu diễn vào biểu đồ cột sau. Tìm các giá trị a, b, c trong biểu đồ.

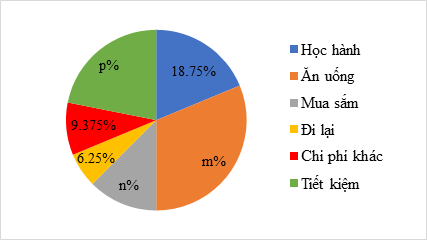
Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

b) Số liệu từ bảng thống kê trên được vào biểu đồ quạt tròn như sau. Hãy tìm các giá trị m, n, p trong biểu đồ.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

c) So sánh ý nghĩa của 2 loại biểu đồ trên.

Hướng dẫn giải

a) Từ bảng thống kê ta có a = 6, b = 4, c = 2.

b) Tổng số tiền thu được trong 1 tháng là:

6 + 10 + 4 + 2 + 3 + 7 = 32 (triệu đồng).

Suy ra: $m % = \frac{10}{32} .100 % = 31, 25 %;$

$n % = \frac{4}{32} .100 % = 12, 5 %;$

$p % = \frac{7}{32} .100 % = 21, 875 % .$

c) Biểu đồ cột cho thấy sự hơn kém về chi tiêu ngân sách của gian đình bạn Nam.

Ví dụ chi tiêu vào việc ăn uống nhiều nhất là 10 triệu đồng, ít nhất là việc đi lại 2 triệu đồng.

Do đó số tiền chi tiêu vào việc ăn uống nhiều hơn đi lại là: 10 – 2 = 8 (triệu đồng).

Trong khi đó, biểu đồ hình quạt cho biết ngoài sự hơn kém về chi tiêu của gia đình bạn Nam, mà còn cho biết tỉ lệ phần trăm chi mỗi việc so với tổng thu nhập của gia đình.

Ví dụ, chi tiêu vào việc ăn uống gấp 5 lần chi tiêu cho việc đi lại và chiếm 31,25% so với tổng thu nhập của gia đình.

Bài 10. Bảng dưới đây thống kê một số yếu tố trong một Trường THCS:

Số lớp học	Số giáo viên	Số học sinh nam	Số học sinh nữ
28	50	670	480

Phân tích bảng thống kê để tìm

a) Số học sinh bình quân trên một giáo viên?

b) Số học sinh bình quân trong một lớp?

Hướng dẫn giải

a) Tổng số học sinh của toàn trường là:

670 + 480 = 1150 (học sinh)

Số học sinh bình quân trên một giáo viên là:

1150 : 50 = 23 (học sinh).

Vậy số học sinh bình quân trên một giáo viên là 23 học sinh.

b) Số học sinh bình quân trong một lớp là:

1150 : 28 ≈ 41(học sinh).

Vậy số học sinh bình quân trong một lớp khoảng 41 học sinh.

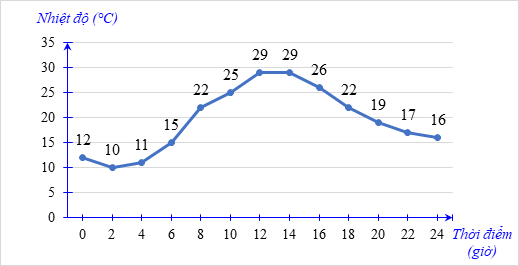
Bài 11. Biểu đồ đoạn thẳng biểu diễn nhiệt trong ngày tại các thời điểm của một địa phương như sau:

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

a) Hãy nhận xét về sự thay đổi nhiệt độ trong các khoảng thời gian: 0h – 2h; 2h – 4h; 4h – 6h; 6h – 8h; 8h – 10h; 10h – 12h; 12h – 14h; 14h – 16h; 16h – 18h; 18h – 20h; 20h – 22h; 22h – 24h.

b) Tính chênh lệch nhiệt độ ngày hôm đó của địa điểm trên, biết chênh lệch nhiệt độ trong ngày bằng hiệu của nhiệt độ cao nhất và nhiệt độ thấp nhất ngày hôm đó.

c) Trong khoảng thời gian nào chúng ta không nên ra ngoài trời vì quá lạnh?

Hướng dẫn giải

a) Dựa vào biểu đồ nhiệt độ tại các thời điểm, ta có nhận xét sau:

• Nhiệt độ tăng trong các khoảng thời gian: 2h – 4h; 4h – 6h; 6h – 8h; 8h – 10h; 10h – 12h.

• Nhiệt độ ổn định trong khoảng thời gian: 12h – 14h.

• Nhiệt độ giảm trong các khoảng thời gian: 0h – 2h; 14h – 16h; 16h – 18h; 18h – 20h; 20h – 22h; 22h – 24h.

b) Dựa vào biểu đồ, ta có nhiệt độ cao nhất vào khoảng thời gian 12h- 14h là 29°C, nhiệt độ thấp nhất vào lúc 2h là 10°C.

Do chênh lệch nhiệt độ trong ngày bằng hiệu của nhiệt độ cao nhất và nhiệt độ thấp nhất ngày hôm đó nên chênh lệch nhiệt độ ngày hôm đó của địa điểm trên là:

29°C - 10°C = 19°C.

c) Trong khoảng thời gian 2h – 4h là khoảng thời gian có nhiệt độ thấp nhất nên sẽ lạnh nhất.

Vậy chúng ta không nên ra ngoài vào khoảng thời gian 2h – 4h.

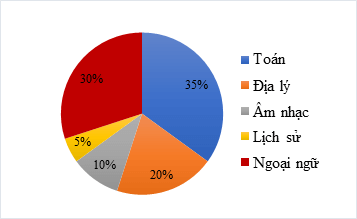
Bài 12. Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ lệ phần trăm) môn học gây hứng thú học tập nhất đối với học sinh của một lớp học. Mỗi học sinh chỉ được chọn 1 môn khi được hỏi ý kiến.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

a) Lập bảng số liệu thống kê theo mẫu sau

Môn học gây hứng thú	Toán	Địa lý	Âm nhạc	Lịch sử	Ngoại ngữ
Tỉ lệ phần trăm	?	?	?	?	?

b) Biết tổng số học sinh của cả lớp là 40 học sinh. Tính số học sinh chọn môn Toán và môn Lịch sử là môn học gây hứng thú nhất.

c) Sau khi phân tích, lớp trưởng nói rằng số bạn lựa chọn môn Ngoại ngữ là môn học gây hứng thú nhất gấp 5 lần số bạn lựa chọn môn Âm nhạc. Khẳng định của bạn lớp trưởng có đúng không? Tại sao?

Hướng dẫn giải

a) Dựa vào biểu đồ ta có bảng số liệu sau:

Môn học gây hứng thú	Toán	Địa lý	Âm nhạc	Lịch sử	Ngoại ngữ
Tỉ lệ phần trăm	35%	20%	10%	5%	30%

b) Số học sinh chọn môn Toán là môn gây hứng thú nhất là:

$\frac{40.35 %}{100 %} = 14$ (học sinh).

Số học sinh chọn môn Lịch sử là môn gây hứng thú nhất là:

$\frac{40.5 %}{100 %} = 2$ (học sinh).

c) Số bạn lựa chọn môn Ngoại ngữ là môn học gây hứng thú nhất gấp số lần số bạn lựa chọn môn Âm nhạc là:

$\frac{30 %}{10 %} = 3$ (lần).

Vậy khẳng định của bạn lớp trưởng là chưa đúng.

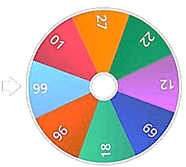
Bài 13. Hình dưới đây mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 12; 18; 22; 27; 69; 96; 99. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

Tính xác suất của các biến cố sau:

a) “Mũi tên chỉ vào hình quạt ghi số là số chia hết cho 3”.

b) “Mũi tên chỉ vào hình quạt ghi số là bội của 22”.

c) “Mũi tên chỉ vào hình quạt ghi số là số chia hết cho 5 dư 2”.

Hướng dẫn giải

a) Có 6 kết quả thuận lợi cho biến cố “Mũi tên chỉ vào hình quạt ghi số là số chia hết cho 3” đó là: 12; 18; 27; 69; 96; 99.

Vì thế xác suất của biến cố đó là: $\frac{6}{8} = \frac{3}{4} .$

b) Có 1 kết quả thuận lợi cho biến cố “Mũi tên chỉ vào hình quạt ghi số là bội của 22” đó là 22.

Vì thế xác suất của biến cố đó là $\frac{1}{8} .$

c) Có 3 kết quả thuận lợi cho biến cố “Mũi tên chỉ vào hình quạt ghi số là số chia hết cho 5 dư 2” đó là: 12; 22; 27.

Vì thế xác suất của biến cố đó là $\frac{3}{8} .$

Bài 14. Bác Hà còn một miếng đất trống để trồng cây gồm có 8 loại cây cho bác trồng: Cây ngô; Cây chè; Cây cao cao; Cây cao su; Cây sắn; Cây cà phê; Cây điều; Cây củ cải đường. Mảnh đất này chỉ trồng đúng 1 loại cây. Chọn ra ngẫu nhiên một cây trong các cây trên.

Tính xác suất mỗi biến cố sau:

a) “Cây được chọn ra là cây lương thực”.

b) “Cây được chọn ra là cây công nghiệp”.

Hướng dẫn giải

a) Có 2 kết quả thuận lợi cho biến cố “Cây được chọn ra là cây lương thực” đó là cây ngô; cây sắn.

Vì thế xác suất của biến cố đó là: $\frac{2}{8} = \frac{1}{4} .$

b) Có 6 kết quả thuận lợi cho biến cố “Cây được chọn ra là cây công nghiệp” đó là cây chè; cây cao cao; cây cao su; cây cà phê; cây điều; cây củ cải đường.

Vì thế xác suất của biến cố đó là: $\frac{6}{8} = \frac{3}{4} .$

Bài 15. Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 100.

a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?

b) Tính xác suất của mỗi biến cố sau:

A: “Số tự nhiên được viết ra là số chẵn”;

B: “Số tự nhiên được viết ra là số tròn chục”;

C: “Số tự nhiên được viết ra là bình phương của một số tự nhiên”.

Hướng dẫn giải

a) Số tự nhiên có hai chữ số nhỏ hơn 100 là 10; 11; 12; …….; 99.

Do đó, có 90 cách viết ngẫu nhiên một số tự nhiên như vậy.

b) • Có 45 kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số chẵn” đó là 12; 14; 16; 18; 22;…….; 92; 94; 96; 98.

Vì thế, xác suất của biến cố A là $\frac{45}{90} = \frac{1}{2} .$

• Có 45 kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số tròn chục” đó là 10; 20; 30; 40; 50; 60; 70; 80; 90.

Vì thế, xác suất của biến cố đó là $\frac{9}{90} = \frac{1}{10} .$

• Có 6 kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là bình phương của một số tự nhiên” đó là 16; 25; 36; 49; 64; 81.

Vì thế, xác suất của biến cố đó là $\frac{6}{90} = \frac{1}{15} .$

Ví dụ 16. Một hộp có 30 quả bóng được đánh số từ 1 đến 30, đồng thời các quả bóng từ 1 đến 10 được sơn màu cam và các quả bóng còn lại được sơn màu xanh; các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiện một quả bóng trong hộp.

Tính xác suất của các biến cố sau:

a) “Quả bóng được lấy ra được sơn màu cam”.

b) “Quả bóng được lấy ra ghi số tròn chục”.

Hướng dẫn giải

a) Có 10 kết quả thuận lợi cho biến cố “Quả bóng được lấy ra được sơn màu cam” đó là 1; 2; 3; 4; 5; 6; 7; 8; 9; 10.

Vì thế xác suất của biến cố đó là: $\frac{10}{30} = \frac{1}{3} .$

b) Có 3 kết quả thuận lợi cho biến cố “Quả bóng được lấy ra ghi số tròn chục” đó là 10; 20; 30.

Vì thế xác suất của biến cố đó là: $\frac{3}{30} = \frac{1}{10} .$

Bài 17. Một trung tâm du học xuất khẩu ra nước ngoài gồm có 60 học sinh trong đó có 25 học sinh học tiếng Trung; 25 học sinh học tiếng Nhật; 7 học sinh học tiếng Hàn; 3 học sinh học cả tiếng Trung và tiếng Hàn. Chọn ngẫu nhiện một học sinh từ trung tâm đó.

Tính xác suất của các biến cố sau:

a) “Học sinh được chọn học tiếng Trung”.

b) “Học sinh được chọn học tiếng Nhật”.

c) “Học sinh được chọn học tiếng Hàn”.

d) “Học sinh được chọn học cả tiếng Trung và tiếng Hàn”.

Hướng dẫn giải

a) Có 25 kết quả thuận lợi cho biến cố “Học sinh được chọn học tiếng Trung”.

Vì thế, xác suất của biến cố đó là: $\frac{25}{60} = \frac{5}{12} .$

b) Có 25 kết quả thuận lợi cho biến cố “Học sinh được chọn học tiếng Nhật”.

Vì thế, xác suất của biến cố đó là: $\frac{25}{60} = \frac{5}{12} .$

c) Có 7 kết quả thuận lợi cho biến cố “Học sinh được chọn học tiếng Hàn”.

Vì thế, xác suất của biến cố đó là $\frac{7}{60} .$

d) Có 32 kết quả thuận lợi cho biến cố “Học sinh được chọn học cả tiếng Trung và tiếng Hàn”.

Vì thế, xác suất của biến cố đó là $\frac{32}{60} = \frac{8}{15} .$

Bài 18. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” trong mỗi trường hợp sau:

a) Tung một đồng xu 15 lần liên tiếp, có 10 lần xuất hiện mặt S.

b) Tung một đồng xu 40 lần liên tiếp, có 22 lần xuất hiện mặt N.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

Hướng dẫn giải

a) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” là: $\frac{10}{15} = \frac{2}{3} .$

b) Khi tung đồng xu 40 lần liên tiếp, có 22 lần xuất hiện mặt N nên mặt S xuất hiện 18 lần.

Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” là: $\frac{18}{40} = \frac{9}{20} .$

Bài 19.

a) Gieo một con xúc xắc 20 lần liên tiếp, có 14 lần xuất hiện mặt 5 chấm. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 5 chấm”.

b) Gieo một con xúc xắc 40 lần liên tiếp, có 18 lần xuất hiện mặt 2 chấm. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 2 chấm”.

c) Gieo một con xúc xắc 24 lần liên tiếp, có 6 lần xuất hiện mặt 6 chấm. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 6 chấm”.

Tổng hợp Lý thuyết Toán 8 Chương 6 Cánh diều

Hướng dẫn giải

a) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 3 chấm” là $\frac{14}{20} = \frac{7}{10} .$

b) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 1 chấm” là $\frac{18}{40} = \frac{9}{20} .$

c) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 2 chấm” là $\frac{6}{24} = \frac{1}{4} .$

Bài 20. Một hộp chứa bốn chiếc kẹp nơ tóc có kích thước và mẫu mã giống nhau, trong đó có 1 chiếc màu xanh, 1 chiếc màu hồng, 1 chiếc màu vàng, 1 chiếc màu nâu. Mỗi lần bạn Lan lấy ngẫu nhiên một chiếc nơ trong hộp, ghi lại màu của chiếc nơ được lấy ra và bỏ lại chiếc nơ đó vào hộp. Trong 10 lần lấy liên tiếp, có 3 lần xuất hiện màu xanh, 2 lần xuất hiện màu vàng, 4 lần xuất hiện màu hồng.

Tính xác suất thực nghiệm của mỗi biến cố sau:

a) “Chiếc kẹp lấy ra là màu hồng”.

b) “Chiếc kẹp lấy ra là màu nâu”.

Hướng dẫn giải

a) Xác suất thực nghiệm của biến cố “Chiếc kẹp lấy ra là màu hồng” là $\frac{4}{10} = \frac{2}{5} .$

Trong 10 lần lấy tiếp, do kẹp nơ màu xanh xuất hiện 3 lần, kẹp nơ màu vàng xuất hiện 2 lần và kẹp nơ màu hồng xuất hiện 4 lần.

Suy ra, kẹp nơ màu nâu xuất hiện: 10 – 3 – 2 – 4 = 1 (lần).

Vì vậy, xác suất thực nghiệm của biến cố “Quả bóng lấy ra là quả bóng màu đỏ” là $\frac{1}{45} .$

Bài 21. Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số lẻ” ngày càng gần với số thực nào?

Hướng dẫn giải

Tập hợp các kết quả có thể xảy ra đối với số chấm trên mặt xuất hiện khi gieo xúc xắc là:

A = {1 chấm; 2 chấm; 3 chấm; 4 chấm; 5 chấm; 6 chấm}.

Các kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số lẻ” là 1 chấm; 3 chấm; 5 chấm. Do đó, có 3 kết quả thuận lợi cho biến cố đó.

Vì vậy, xác suất của biến cố đó là $\frac{3}{6} = \frac{1}{2} .$

Vậy khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số lẻ” ngày càng gần với $\frac{1}{2} .$

Bài 22. Một hộp có 20 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá 20, hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp. Sau 25 lần lấy thẻ liên tiếp , thẻ ghi số 3 được lấy ra 5 lần, thẻ ghi số 1 được lấy ra 10 lần.

a) Tính xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số 3” trong trò chơi trên.

b) Tính xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số 1” trong trò chơi trên.

c) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số là số chia hết cho 6” với xác suất của biến cố đó khi số lần rút thẻ ngày càng lớn.

Hướng dẫn giải

Tập hợp các kết quả có thể xảy ra đối với số được ghi trên thẻ khi lấy ngẫu nhiên một chiếc thẻ trong hộp là A = {1; 2; 3; 4; ...; 20}.

Tập hợp A có 20 phần tử.

a)⦁ Xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số 3” là $\frac{5}{25} = \frac{1}{5} .$

⦁ Xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số 1” là $\frac{10}{25} = \frac{2}{5} .$

b) Các kết quả thuận lợi cho biến cố “Thẻ rút ra ghi số chia hết cho 6” là 6; 12; 18. Do đó, có 3 kết quả thuận lợi với biến cố đó.

Vì vậy, xác suất của biến cố “Thẻ rút ra ghi số chia hết cho 6” là $\frac{3}{20} .$

Vậy khi số lần rút thẻ ngày càng lớn thì xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số chia hết cho 3” ngày càng gần với $\frac{3}{20} .$

Học tốt Toán 8 Chương 6

Các bài học để học tốt tổng hợp Toán 8 Chương 6 Toán lớp 8 hay khác:

(199k) Xem Khóa học Toán 8 CD

Xem thêm tóm tắt lý thuyết Toán lớp 8 Cánh diều hay khác:

Xem thêm các tài liệu học tốt lớp 8 hay khác:

HOT 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k)

Tủ sách VIETJACK shopee lớp 6-8 (2025):

TÀI LIỆU CLC DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 8

+ Bộ giáo án, bài giảng powerpoint, đề thi file word có đáp án 2025 tại https://tailieugiaovien.com.vn/

+ Hỗ trợ zalo: VietJack Official

+ Tổng đài hỗ trợ đăng ký : 084 283 45 85

Đề thi giữa kì, cuối kì 8

( 172 tài liệu )

Bài giảng Powerpoint Văn, Sử, Địa 8....

( 40 tài liệu )

Giáo án word 8

( 78 tài liệu )

Chuyên đề dạy thêm Toán, Lí, Hóa ...8

( 74 tài liệu )

Đề thi HSG 8

( 5 tài liệu )

Trắc nghiệm đúng sai 8

( 12 tài liệu )

xem tất cả

Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.

Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:

Loạt bài Giải bài tập Toán 8 Cánh diều hay nhất, chi tiết của chúng tôi được biên soạn bám sát sgk Toán 8 Cánh diều (Tập 1 & Tập 2) (NXB ĐH Sư phạm).

Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.

Trang trước Trang sau