18 Bài tập Tứ giác (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8
Với 18 bài tập trắc nghiệm Tứ giác Toán lớp 8 có đáp án và lời giải chi tiết đầy đủ
các mức độ, có đúng sai, trả lời ngắn sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.
18 Bài tập Tứ giác (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Câu 1. Hãy chọn câu sai trong các câu sau:
Quảng cáo
A. Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
B. Tổng các góc của một tứ giác bằng 180°.
C. Tổng các góc của một tứ giác bằng 360°.
D. Tứ giác ABCD là hình gồm các đoạn thẳng AB, BC, DC, DA, trong đó bất kì hai đoạn thẳng nào cũng không nằm trên một đường thẳng.
Hiển thị đáp án
Đáp án đúng là: B
Tổng các góc của một tứ giác bằng 360° nên câu sai là: tổng các góc của một tứ giác bằng 180°.
Câu 2. Các góc của tứ giác có thể là
A. 4 góc nhọn.
B. 4 góc tù.
C. 4 góc vuông.
D. 1góc vuông, 3 góc nhọn.
Hiển thị đáp án
Đáp án đúng là: D
Tổng các góc trong một tứ giác bằng 360°.
Các góc của tứ giác có thể là 4 góc vuông vì khi đó tổng các góc của tứ giác này bằng 360°.
Các trường hợp còn lại không thỏa mãn định lí tổng các góc trong tam giác.
Quảng cáo
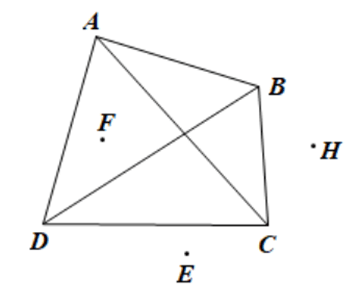
Câu 3. Cho hình vẽ dưới đây. Chọn khẳng định sai trong các câu sau
A. Hai đỉnh kề nhau: A và B; A và D.
B. Hai đỉnh đối nhau: A và C; B và D.
C. Đường chéo: AC, BD.
D. Các điểm nằm trong tứ giác là E, F và các điểm nằm ngoài tứ giác là H.
Hiển thị đáp án
Đáp án đúng là: D
Từ hình vẽ ta có thể có các điểm E, H nằm bên ngoài tứ giác và điểm F nằm bên trong tứ giác ABCD nên D sai.
Câu 4. Tứ giác ABCD có A ^ = 50 ° ; B ^ = 123 ° ; D ^ = 20 °
A. 160°
B. 167°
C. 170°
D. 130°
Hiển thị đáp án
Đáp án đúng là: B
Trong tứ giác ABCD là:
A ^ + B ^ + C ^ + D ^ = 360 °
⇒ C ^ = 360 ° − A ^ − B ^ − D ^ = 360 ° − 50 ° − 123 ° − 20 ° = 167 °
Câu 5. Cho tứ giác ABCD trong đó: A ^ + B ^ = 140 ° . C ^ + D ^
Quảng cáo
A. 220°
B. 200°
C. 160°
D. 130°
Hiển thị đáp án
Đáp án đúng là: A
Trong tứ giác ABCD có:
A ^ + B ^ + C ^ + D ^ = 360 °
⇒ C ^ + D ^ = 360 ° − A ^ + B ^ = 360 ° − 140 ° = 220 °
Tổng các góc trong một tứ giác bằng 360o
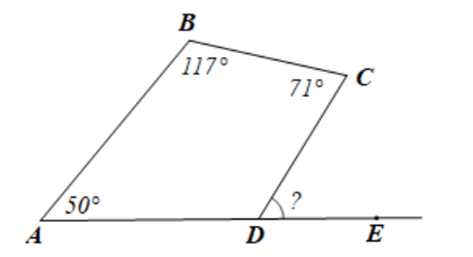
Câu 6. Cho tứ giác ABCD có A ^ = 50 ° ; B ^ = 117 ° ; C ^ = 71 °
A. 113°
B. 107°
C. 58°
D. 83°
Hiển thị đáp án
Đáp án đúng là: C
CDE ^
D ^ = 360 ° − A ^ + B ^ + C ^
D ^ = 360 ° − 50 ° + 117 ° + 71 °
D ^ = 122 °
Vì ADC ^ CDE ^
CDE ^ = 180 ° − D ^ = 180 ° − 122 ° = 58 °
Góc ngoài và góc trong tứ giác tại một đỉnh là hai góc kề bù.
Câu 7. Tứ giác ABCD có A ^ = 100 ° ; B ^ = 120 ° ; C ^ − D ^ = 20 °
A. C ^ = 100 ° ; D ^ = 80 °
B. C ^ = 75 ° ; D ^ = 55 °
C. C ^ = 80 ° ; D ^ = 60 °
D. C ^ = 85 ° ; D ^ = 65 °
Hiển thị đáp án
Đáp án đúng là: C
Trong tứ giác ABCD ta có:
A ^ + B ^ + C ^ + D ^ = 360 °
⇒ C ^ + D ^ = 360 ° − A ^ − B ^ = 360 ° − 100 ° − 120 ° = 140 ° (1)
Mà C ^ − D ^ = 20 °
Từ (1), (2) suy ra: C ^ = 80 ° ; D ^ = 60 °
Quảng cáo
Câu 8. Cho tứ giác ABCD có góc ngoài tại đỉnh D bằng 50°; góc ngoài tại đỉnh A bằng 100°. Tổng A ^ + D ^
A. 100o
B. 130o
C. 80o
D. 210o
Hiển thị đáp án
Đáp án đúng là: D
Vì góc ngoài đỉnh D bằng 50° nên góc trong tại đỉnh D là: D ^ = 180 ° − 50 ° = 130 °
Vì góc ngoài tại đỉnh A bằng 100o nên góc trong tại đỉnh A là: A ^ = 180 ° − 100 ° = 80 °
Suy ra: A ^ + D ^ = 80 ° + 130 ° = 210 °
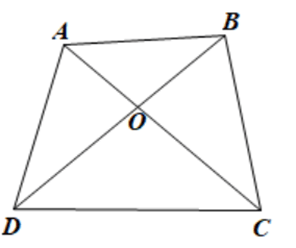
Câu 9. Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng?
A. O A + O B + O C + O D < A B + B C + C D + D A
B. OA + OB + OC + OD > AB + BC + CD + DA
C. OA + OB + OC + OD < 1 2 AB + BC + CD + DA
D. O A − O B + O C − O D > A B + B C + C D + D A
Hiển thị đáp án
Đáp án đúng là: A
Xét tam giác ABC:
A B + B C > A C
Tương tự, lần lượt các tam giác BCD, CDA, DAB ta có:
B C + C D > B D
C D + D A > C A
DA + AB > DB
Cộng vế với vế ta được các bất đẳng thức trên ta được:
A B + B C + C D + C D + D A + D A + A B > A C + B D + C A + D B
⇔ 2 A B + B C + C D + D A > 2 A C + B D
⇔ A B + B C + C D + D A > A C + B D
Mà: A C + B D = O A + O C + O B + O D
⇔ O A + O B + O C + O D < A B + B C + C D + D A
Vậy ta có: O A + O B + O C + O D < A B + B C + C D + D A
Câu 10. Cho tứ giác ABCD biết số đo của các góc A ^ , B ^ , C ^ , D ^ A ^ , B ^ , C ^ , D ^
A. 80 ° ; 60 ° ; 100 ° ; 120 °
B. 90 ° ; 40 ° ; 70 ° ; 60 °
C. 60 ° ; 80 ° ; 100 ° ; 120 °
D. 60 ° ; 60 ° ; 100 ° ; 120 °
Hiển thị đáp án
Đáp án đúng là: A
Vì số đo của các góc A ^ , B ^ , C ^ , D ^ A ^ 4 = B ^ 3 = C ^ 5 = D ^ 6 = A ^ + B ^ + C ^ + D ^ 18 = 360 ° 18 = 20 °
Do đó: A ^ = 20 ° .4 = 80 °
B ^ = 20 ° .3 = 60 °
C ^ = 20 ° .5 = 100 °
D ^ = 20 ° .6 = 120 °
Nên số đo các góc A ^ , B ^ , C ^ , D ^ 80 ° ; 60 ° ; 100 ° ; 120 °
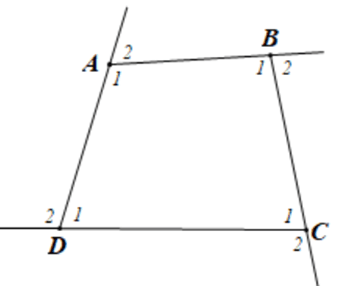
Câu 11. Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
A. 300°
B. 270°
C. 180°
D. 360°
Hiển thị đáp án
Đáp án đúng là: D
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: A 2 ^ ; B 2 ^ ; C 2 ^ ; D 2 ^
Khi đó ta có:
A 1 ^ + A 2 ^ = 180 ° ⇒ A 2 ^ = 180 ° − A 1 ^
B 1 ^ + B 2 ^ = 180 ° ⇒ B 2 ^ = 180 ° − B 1 ^
C 1 ^ + C 2 ^ = 180 ° ⇒ C 2 ^ = 180 ° − C 1 ^
D 1 ^ + D 2 ^ = 180 ° ⇒ D 2 ^ = 180 ° − D 1 ^
Suy ra:
A 2 ^ + B 2 ^ + C 2 ^ + D 2 ^ = 180 ° − A 1 ^ + 180 ° − B 1 ^ + 180 ° − C 1 ^ + 180 ° − D 1 ^
A 2 ^ + B 2 ^ + C 2 ^ + D 2 ^ = 720 ° − A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^
A 2 ^ + B 2 ^ + C 2 ^ + D 2 ^ = 720 ° − 360 ° = 360 °
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng 360°
Câu 12. Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là 200o . Số đo các góc ngoài tại hai đỉnh A, D là
A. 160°
B. 260°
C. 180°
D. 100°
Hiển thị đáp án
Đáp án đúng là: A
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là: A 2 ^ ; B 2 ^ ; C 2 ^ ; D 2 ^
Khi đó ta có:
A 1 ^ + A 2 ^ = 180 ° ⇒ A 2 ^ = 180 ° − A 1 ^
B 1 ^ + B 2 ^ = 180 ° ⇒ B 2 ^ = 180 ° − B 1 ^
C 1 ^ + C 2 ^ = 180 ° ⇒ C 2 ^ = 180 ° − C 1 ^
D 1 ^ + D 2 ^ = 180 ° ⇒ D 2 ^ = 180 ° − D 1 ^
Suy ra:
A 2 ^ + B 2 ^ + C 2 ^ + D 2 ^ = 180 ° − A 1 ^ + 180 ° − B 1 ^ + 180 ° − C 1 ^ + 180 ° − D 1 ^
A 2 ^ + B 2 ^ + C 2 ^ + D 2 ^ = 720 ° − A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^
A 2 ^ + B 2 ^ + C 2 ^ + D 2 ^ = 720 ° − 360 ° = 360 °
Vậy số đo 4 góc ngoài tứ giác tại 4 đỉnh A, B, C, D bằng 360°
Mà tổng số đo góc ngoài hai đỉnh B, C bằng 200°nên tổng số đo góc ngoài tại hai đỉnh A, D bằng 360 ° − 200 ° = 160 °
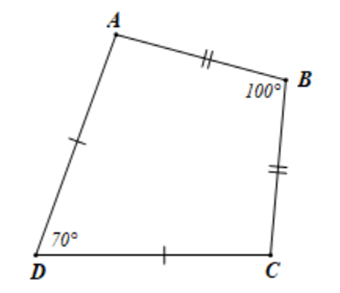
Câu 13. Tứ giác ABCD có AB = BC; CD = DA , B ^ = 100 ° ; D ^ = 70 ° A ^ , C ^
A. A ^ = C ^ = 95 °
B. A ^ = 95 ° ; C ^ = 55 °
C. A ^ = C ^ = 85 °
D. A ^ = 55 ° ; C ^ = 100 °
Hiển thị đáp án
Đáp án đúng là: A
Xét tam giác ABC có AB = AC
⇒ ΔABC B ^ = 100 °
⇒ BAC ^ = BCA ^ = 180 ° − 100 ° 2 = 40 °
Xét tam giác ADC có CD = DA
⇒ ΔADC ADC ^ = 70 °
⇒ DAC ^ = DCA ^ = 180 ° − 70 ° 2 = 55 °
Từ đó ta có:
A ^ = BAD ^ = BAC ^ + CAD ^
⇒ A ^ = BAD ^ = 40 ° + 55 ° = 95 °
Vậy C ^ = BCD ^ = BCA ^ + ACD ^
⇒ C ^ = BCD ^ = 40 ° + 55 ° = 95 °
Vậy A ^ = C ^ = 95 °
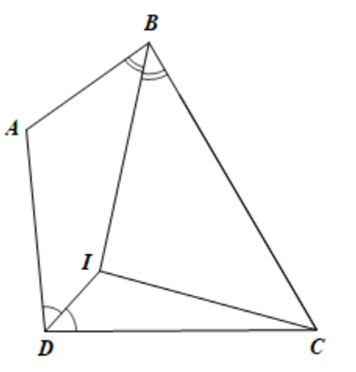
Câu 14. Tứ giác ABCD có: A ^ − C ^ = 60 ° .
Số đo góc BID là
A. 150°
B. 120°
C. 140°
D. 100°
Hiển thị đáp án
Đáp án đúng là: D
Xét tam giác BIC có:
IBC ^ = I 1 ^ − BCI ^
Xét tam giác DIC có:
IDC ^ = I 2 ^ − ICD ^
Nên: IBC ^ + IDC ^ = I 1 ^ + I 2 ^ − C 1 ^ + C 2 ^ = BID ^ − C ^
Tứ giác ABID:
ABI ^ + ADI ^ = 360 ° − A ^ − BID ^
Do: ADI ^ = IDC ^
Nên: IBC ^ + IDC ^ = ABI ^ + ADI ^
Hay
BID ^ − C ^ = 360 ° − A ^ − BID ^
⇔ 2 BID ^ = 360 ° − A ^ − C ^ = 360 ° − 1 60 ° = 200 °
Suy ra: BID ^ = 100 °
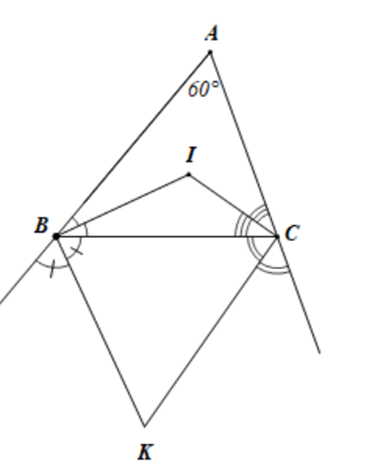
Câu 15. Tam giác ABC có A ^ = 60 ° , BIC ^ ; BKC ^
A. BIC ^ = 100 ° ; BKC ^ = 80 °
B. BIC ^ = 90 ° ; BKC ^ = 90 °
C. BIC ^ = 60 ° ; BKC ^ = 120 °
D. BIC ^ = 120 ° ; BKC ^ = 60 °
Hiển thị đáp án
Đáp án đúng là: D
Xét tam giác ABC có:
A ^ + ABC ^ + BCA ^ = 180 °
⇒ ABC ^ + BCA ^ = 120 °
Vì BI là phân giác BAC ^ ⇒ CBI ^ = 1 2 BAC ^
Vì CI là phân giác BCA ^ ⇒ BCI ^ = 1 2 BCA ^
Từ đó: CBI ^ + BCI ^ = 1 2 BAC ^ + BCA ^ = 1 2 .120 ° = 60 °
Xét tam giác BCI có: BCI ^ + BIC ^ + CBI ^ = 180 °
Nên: BIC ^ = 180 ° − BCI ^ + CBI ^ = 180 ° − 60 ° = 120 °
Vì BI là phân giác BAC ^ ⇒ CBI ^ = 1 2 BAC ^
Vì BK là phân giác CBx ^ ⇒ CBK ^ = 1 2 CBx ^
Suy ra: CBK ^ + CBI ^ = 1 2 CBx ^ + ABC ^ = 1 2 .180 ° = 90 °
Hay IBK ^ = 90 °
Tương tự ta có: ICK ^ = 90 °
Xét tứ giác BICK có:
BIC ^ + IBC ^ + ICK ^ + BKC ^ = 360 °
⇒ BKC ^ = 360 ° − 90 ° − 90 ° − 120 ° = 60 °
Vậy BIC ^ = 120 ° ; BKC ^ = 60 °
Phần II. Trắc nghiệm đúng, sai
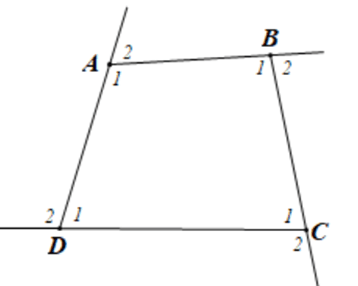
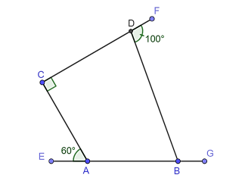
Câu hỏi. Cho hình vẽ:
a) C D B ^ = 80 ° .
b) C A B ^ = 110 ° .
c) D B A ^ = 70 ° .
d) D B G ^ = 100 ° .
Hiển thị đáp án
a) Đúng.
Ta có: C D B ^ + F D B ^ = 180 ° C D B ^ = 180 ° − F D B ^ = 180 ° − 100 ° = 80 ° .
Vậy C D B ^ = 80 ° .
b) Sai.
Ta có: C A B ^ + C A E ^ = 180 ° C A B ^ = 180 ° − C A E ^ = 180 ° − 60 ° = 120 ° .
Vậy C A B ^ = 120 ° .
c) Đúng.
Tứ giác ABCD có: C A B ^ + D B A ^ + A C D ^ + C D B ^ = 360 °
Do đó, D B A ^ = 360 ° − C A B ^ − A C D ^ − C D B ^ = 360 ° − 120 ° − 90 ° − 80 ° = 70 ° . D B A ^ = 70 ° .
d) Sai.
Ta có: D B G ^ + D B A ^ = 180 ° D B G ^ = 180 ° − D B A ^ = 180 ° − 70 ° = 110 ° .
Vậy D B G ^ = 110 ° .
Phần III. Trắc nghiệm trả lời ngắn
Câu 1. Cho tứ giác ABCD có A ^ , B ^ , C ^ , D ^ 2 ; 3 ; 6 ; 7. C ^ bằng bao nhiêu độ?
Hiển thị đáp án
Đáp án: 120
Vì A ^ , B ^ , C ^ , D ^ ần lượt tỉ lệ với 2 ; 3 ; 6 ; 7 A ^ 2 = B ^ 3 = C ^ 6 = D ^ 7 .
Theo tính chất của dãy tỉ số bằng nhau ta có:
A ^ 2 = B ^ 3 = C ^ 6 = D ^ 7 = A ^ + B ^ + C ^ + D ^ 2 + 3 + 6 + 7 = 360 ° 18 = 20 ° .
Do đó, C ^ = 6 ⋅ 20 ° = 120 ° . C ^ = 120 ° .
Câu 2. Cho tứ giác ABCD gọi E là giao điểm của các tia phân giác các góc C, D của tứ giác ABCD. Khi đó, C E D ^ = A ^ + B ^ .
Hiển thị đáp án
Đáp án: 2
Vì CE là tia phân giác của B C D ^ E C D ^ = 1 2 B C D ^ .
Vì DE là tia phân giác của A D C ^ E D C ^ = 1 2 A D C ^ .
Tam giác CDE có: C E D ^ + C D E ^ + E C D ^ = 180 °
Nên C E D ^ = 180 ° − C D E ^ + E C D ^ = 180 ° − 1 2 B C D ^ + A D C ^ = 180 ° − 1 2 360 ° − A ^ + B ^ = 1 2 A ^ + B ^ .
Do đó, 2 C E D ^ = A ^ + B ^ . Vậy số thích hợp điền vào dấu “…” là 2
Xem thêm bài tập trắc nghiệm Toán lớp 8 Kết nối tri thức có đáp án hay khác:
Xem thêm các tài liệu học tốt lớp 8 hay khác:
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:
Loạt bài Giải bài tập Toán 8 hay nhất, chi tiết của chúng tôi được biên soạn bám sát sgk Toán 8 Kết nối tri thức (Tập 1 & Tập 2) (NXB Giáo dục).
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web
Giải bài tập lớp 8 Kết nối tri thức khác




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

