Bài toán thực tế lớp 10 Hệ thức lượng trong tam giác

Bài toán thực tế lớp 10 Hệ thức lượng trong tam giác có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều với bài tập đa dạng giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 10.

Bài toán thực tế lớp 10 Hệ thức lượng trong tam giác

Xem thử

Chỉ từ 300k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 10 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

A. KIẾN THỨC CẦN NHỚ

1. Định lí côsin trong tam giác

Định lí côsin

Với mọi tam giác ABC, nếu đặt BC = a, CA = b, AB = c thì ta luôn có:

$\begin{array}{l}{a}^2=b^2+c^2-2bc\cos A\end{array}$

$b^2=c^2+a^2-2ca\cos B$

$c^2=a^2+b^2-2ab\cos C$

Hệ quả

$\cos A=\frac{b^2+c^2-a^2}{2bc};$$\cos B=\frac{c^2+a^2-b^2}{2ca};$$\cos C=\frac{a^2+b^2-c^2}{2ab}.$

2. Định lí sin trong tam giác

Định lí sin

Với mọi tam giác ABC, đặt BC = a, CA = b, AB = c, ta có: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R,$

trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.

Hệ quả

a = 2R sinA

$\sin A=\frac{a}{2R}$

b = 2R sinB

$\sin B=\frac{b}{2R}$

c = 2R sinC

$\sin C=\frac{c}{2R}$

3. Các công thức tính diện tích tam giác

Cho tam giác ABC. Ta kí hiệu:

- $h_a,h_b,h_c$ là độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB.

- R, r lần lượt là bán kính các đường tròn ngoại tiếp và nội tiếp của tam giác.

- p là nửa chu vi tam giác.

- S là diện tích tam giác.

Ta có các công thúc tính diện tích tam giác sau:

1) $S=\frac{1}{2}a{h}_a=\frac{1}{2}b{h}_b=\frac{1}{2}c{h}_c$

2) $S=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B$

3) $S=\frac{abc}{4R}$

4) S = pr;

5) $S=\sqrt{p(p-a)(p-b)(p-c)}$ (công thức Heron).

B. BÀI TẬP VẬN DỤNG

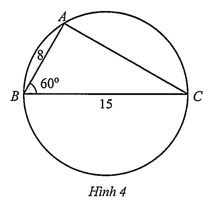
Câu 1: Từ một tấm bìa hình tròn, bạn An cắt ra được một hình tam giác có các cạnh AB = 8cm, BC = 15cm và góc $B={60}^{°}$ (Hình 4). Tính độ dài cạnh AC và bán kính R của miếng bìa.

Giải

Áp dụng định lí côsin cho tam giác ABC ta có: $A{C}^2=A{B}^2+B{C}^2-2AB\cdot BC\cdot \cos B$ $=8^2+{15}^2-2\cdot 8\cdot 15\cdot \cos {60}^{°}=169.$

Suy ra $AC=\sqrt{169}=13( cm)$.

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{AC}{\sin B}=2R$.

Suy ra $R=\frac{AC}{2\sin B}=\frac{13}{2\sin {60}^{°}}=\frac{13\sqrt{3}}{3}( cm)$

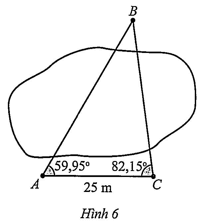
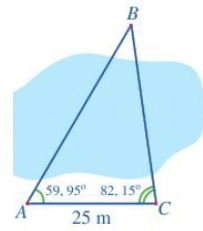
Câu 2: Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết $AC=25 m,\widehat{BAC}=59,{95}^{°},\widehat{BCA}=82,{15}^{°}$ (Hình 6).

Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Giải

Xét tam giác ABC, ta có:

$\widehat{ABC}={180}^{°}-59,{95}^{°}-82,{15}^{°}=37,9^{°}$

Áp dụng định lí sin ta có: $\frac{AB}{\sin C}=\frac{AC}{\sin B}$. Do đó $AB=\frac{25\sin 82,{15}^{°}}{\sin 37,9^{°}}\approx 40( m)$.

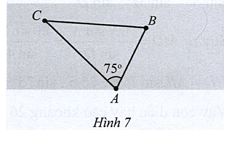
Câu 3: Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc ${75}^{°}$. Tàu thứ nhất đi với tốc độ 8 hải lí một giờ và tàu thứ hai đi với tốc độ 12 hải lí một giờ. Hỏi sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?

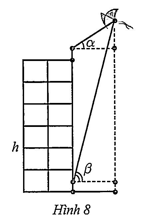
Câu 4: Người A đứng ở đỉnh của tòa nhà và quan sát chiều diều, nhận thấy góc nâng (góc nghiên giữa phương từ mắt của người A tới chiếc diều và phương nằm ngan) là $\alpha =35°$; khoảng cách từ đỉnh tòa nhà tới mắt người A là 1,5m. Cùng lúc đó ở dưới chân tòa nhà, người B cũng quan sát chiếc diều và thấy góc nâng là $\beta =75°$; khoảng cách từ mặt đất đến mắt người B cũng là 1,5m. Biết chiều cao của tòa nhà là h = 20m (hình 8).

Chiếc diều bay cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng đơn vị)?

Câu 5: Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết $AC=25 m,\widehat{BAC}=59,{95}^{°};\widehat{BCA}=82,{15}^{°}$. Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Câu 6: Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc ${75}^{°}$. Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ và tàu thứ hai chạy với tốc độ 12 hải lí một giờ. Sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?

Câu 7: Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là $\alpha ={35}^{°}$; khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là $\beta ={75}^{°}$; khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5m. Biết chiều cao của tòa nhà là h = 20m (Hình). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?

................................

................................

................................

Xem thử

Xem thêm Chuyên đề Toán thực tế lớp 10 chương trình mới có lời giải hay khác:

• Bài toán thực tế lớp 10 Bất phương trình và hệ bất phương trình bậc nhất 2 ẩn

• Bài toán thực tế lớp 10 Vectơ

• Bài toán thực tế lớp 10 Hàm số bậc hai

• Bài toán thực tế lớp 10 Hai phương trình quy về phương trình bậc hai

• Bài toán thực tế lớp 10 Các số đặc trưng đo xu thế trung tâm

• Bài toán thực tế lớp 10 Đường thẳng

---