Trọn bộ Công thức Toán lớp 7 Chương 2: Tam giác quan trọng

---

---

Trọn bộ Công thức Toán lớp 7 Chương 2: Tam giác quan trọng

Nhằm mục đích giúp học sinh dễ dàng nhớ và nắm vững các công thức Toán 7, VietJack biên soạn tài liệu trọn bộ công thức Toán 7 Chương 2: Tam giác đầy đủ công thức quan trọng, lý thuyết và bài tập tự luyện giúp học sinh vận dụng và làm bài tập thật tốt môn Toán lớp 7.

• Tổng ba góc trong một tam giác hay, chi tiết

• Công thức tính góc ngoài tam giác hay, chi tiết

• Các trường hợp bằng nhau của hai tam giác thường hay, chi tiết

• Tính chất tam giác vuông, tam giác cân, tam giác đều, tam giác vuông cân hay, chi tiết

• Công thức Định lý Py-ta-go và định lý Py-ta-go đảo hay, chi tiết

• Các trường hợp bằng nhau của tam giác vuông hay, chi tiết

---

---

---

Tổng ba góc trong một tam giác hay, chi tiết

I. Lý thuyết

- Tổng ba góc trong của một tam giác bằng $180°$.

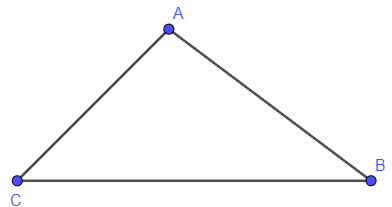
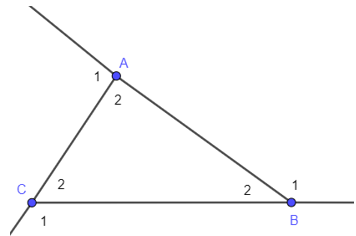
Xét tam giác ABC ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$

- Trong tam giác vuông, hai góc nhọn phụ nhau.

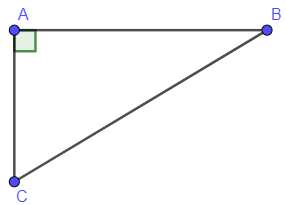
Xét tam giác ABC vuông tại A có $\widehat{B};\widehat{C}$ là hai góc nhọn của tam giác

Khi đó: $\widehat{B}+\widehat{C}=90°$.

II. Các ví dụ:

Ví dụ 1: Cho hình vẽ:

Tính số đo góc $\widehat{A}$.

Lời giải:

Xét tam giác ABC ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lý tổng ba góc trong một tam giác).

Mà $\widehat{B}=30°$; $\widehat{C}=40°$ thay vào ta có:

$\widehat{A}+30°+40°=180°$

$\Rightarrow \widehat{A}=180°-40°-30°=110°$

Vậy $\widehat{A}=110°$.

Ví dụ 2: Cho tam giác ABC vuông tại A có $\widehat{B}=2\widehat{C}$. Tính các góc của tam giác ABC.

Lời giải:

Vì tam giác ABC vuông tại A nên $\widehat{A}=90°$.

Ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lý tổng ba góc trong một tam giác)

Thay $\widehat{A}=90°$ ta có:

$90°+\widehat{B}+\widehat{C}=180°$

$\widehat{B}+\widehat{C}=180°-90°=90°$

Mà $\widehat{B}=2\widehat{C}$ nên $2\widehat{C}+\widehat{C}=90°$

$3\widehat{C}=90°$

$\widehat{C}=30°$

Mà $\widehat{B}=2\widehat{C}$ nên $\widehat{B}=30°.2=60°$

Vậy ba góc của tam giác là $\widehat{A}=90°$; $\widehat{C}=30°$; $\widehat{B}=60°$.

Ví dụ 3: Cho tam giác ABC có ba góc $\widehat{A};\widehat{B};\widehat{C}$ lần lượt tỉ lệ với 2:3:4. Tính số đo các góc của tam giác ABC.

Lời giải:

Gọi số đo ba góc $\widehat{A};\widehat{B};\widehat{C}$ lần lượt là x; y; z

Xét tam giác ABC có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lý tổng ba góc trong một tam giác)

Nên x + y + z = $180°$

Vì ba góc $\widehat{A};\widehat{B};\widehat{C}$ tỉ lệ với 2; 3; 4 nên ta có:

$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{180°}{9}=20°$

$\Rightarrow \left\{\begin{array}{l}\frac{x}{2}=20°\\ \frac{y}{3}=20°\\ \frac{z}{4}=20°\end{array}\right.$ $\Rightarrow \left\{\begin{array}{l}x=40°\\ y=60°\\ y=80°\end{array}\right.$

Vậy ba góc của tam giác ABC là $\widehat{A}=40°$; $\widehat{B}=60°$; $\widehat{C}=80°$

Công thức tính góc ngoài tam giác hay, chi tiết

I. Lý thuyết

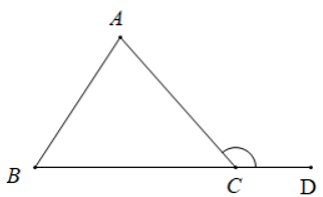
- Định nghĩa: Góc ngoài của một tam giác là góc kề bù với một góc của tam giác ấy.

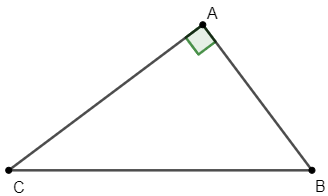
Cho tam giác ABC, vẽ tia đối CD của tia CB, khi đó $\widehat{ACD}$ là góc ngoài tại đỉnh C của tam giác ABC.

- Tính chất

+ Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.

Ta có: ${\widehat{A}}_1;{\widehat{B}}_1;{\widehat{C}}_1$ lần lượt là các góc ngoài tại các đỉnh A; B; C của tam giác ABC.

Khi đó:

$\widehat{A_1}=\widehat{B_2}+\widehat{C_2}$

$\widehat{B_1}=\widehat{A_2}+\widehat{C_2}$

$\widehat{C_1}=\widehat{B_2}+\widehat{A_2}$

- Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó:

${\widehat{A}}_1>{\widehat{B}}_2;{\widehat{A}}_1>{\widehat{C}}_2$(Hình trên)

II. Các ví dụ

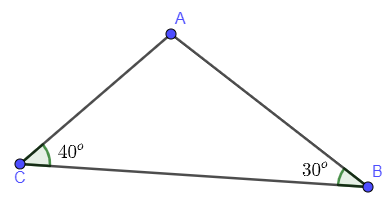
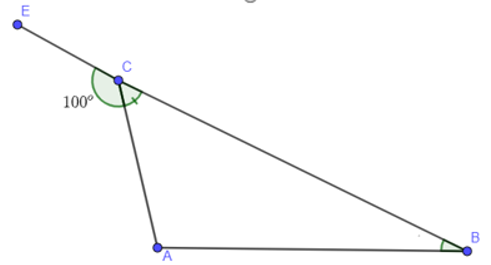
Ví dụ 1: Tính số đo x trong hình vẽ sau

Lời giải:

Xét tam gác ABC có góc $\widehat{CAD}$ là góc ngoài tại đỉnh A của tam giác ABC.

Ta có:

$\widehat{CAD}=\widehat{ACB}+\widehat{CBA}$ (định lý góc ngoài của tam giác)

Mà $\widehat{CAD}=60°$; $\widehat{ACB}=2x$; $\widehat{ABC}=x$ thay vào ta có:

$60°=2x+x$

$3x=60°$

$x=60°:3$

$x=20°$

Vậy $x=20°$.

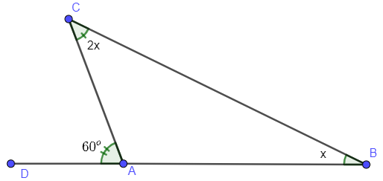
Ví dụ 2: Cho tam giác ABC góc ngoài tại đỉnh C có số đo bằng $100°$, $3\widehat{A}=2\widehat{B}$.

Tính số đo góc $\widehat{B};\widehat{C}$.

Lời giải:

Trên tia đối của tia CB, vẽ tia CE

Ta có: Góc ngoài tại đỉnh C của tam giác ABC là góc $\widehat{ECA}=100°$

Vì $\widehat{ECA}$ và $\widehat{BCA}$ là hai góc kề bù nên:

$\widehat{ECA}+\widehat{BCA}=180°$

Thay $\widehat{ECA}=100°$ và ta có:

$100°+\widehat{BCA}=180°$

$\Rightarrow \widehat{BCA}=180°-100°$

$\Rightarrow \widehat{BCA}=80°$

Xét tam giác ABC ta có:

$\widehat{A}+\widehat{B}=\widehat{ECA}$ (tính chất góc ngoài tam giác)

$\widehat{A}+\widehat{B}=100°$   (1)

Mà $3\widehat{A}=2\widehat{B}\Rightarrow \widehat{A}=\frac{2\widehat{B}}{3}$ thay vào (1) ta có:

$\frac{2\widehat{B}}{3}+\widehat{B}=100°$

$\left(\frac{2}{3}+1\right)\widehat{B}=100°$

$\frac{5}{3}\widehat{B}=100°$

$\widehat{B}=100°:\frac{5}{3}$

$\widehat{B}=60°$

Vậy góc $\widehat{B}=60°$; $\widehat{ACB}=80°$.

....................................

....................................

....................................

Trên đây là phần tóm tắt một số công thức Toán lớp 7 Chương 2: Tam giác năm học 2021 - 2022 quan trọng, để xem chi tiết mời quí bạn đọc vào từng công thức trên!

Xem thêm các bài tổng hợp Công thức Toán lớp 7 đầy đủ, chi tiết khác:

• Chương 1: Số hữu tỉ, Số thực
• Chương 2: Hàm số và đồ thị
• Chương 1: Đường thẳng vuông góc, Đường thẳng song song

---

---

---