Đề kiểm tra 45 phút Hình học 11 Chương 3 có đáp án (Đề 1)
Đề kiểm tra Hình học 11 - Học kì 2
Thời gian làm bài: 45 phút
Phần I: Trắc nghiệm
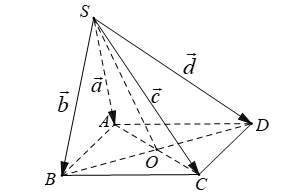
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
- Đặt 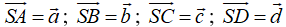
Câu 2: Cho hình hộp ABCD. A'B'C'D'. Gọi I và K lần lượt là tâm của hình bình hành ABB’A’ và BCC’B’. Khẳng định nào sau đây sai?
Câu 3: Trong không gian cho ba đường thẳng phân biệt a,b,c. Khẳng định nào sau đây đúng?
A. Nếu a và b cùng vuông góc với c thì a // b.
B. Nếu a //b và c ⊥ a thì c ⊥ b.
C. Nếu góc giữa a và c bằng góc giữa b và c thì a // b.
D. Nếu a và b cùng nằm trong mp (α) // c thì góc giữa a và c bằng góc giữa b và c.
Câu 4: Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc giữa (IE, JF) bằng:
A. 30° B. 45°
C. 60° D. 90°
Câu 5: Cho tứ diện ABCD có AB = AC = AD = a và 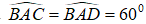
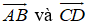
A. 60° B. 45°
C. 120° D. 90°
Câu 6: Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
Câu 7: Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD). Biết 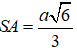
A. 30° B. 45°
C. 60° D.75°
Câu 8: Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là
C. (BCD) ⊥ (AIB).
D. (ACD) ⊥ (AIB).
Phần II: Tự luận
Câu 1: Trong mặt phẳng (P), cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Khoảng cách từ A đến (SBC) bằng:
Câu 2: Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a và
Đáp án & Hướng dẫn giải
Phần I: Trắc nghiệm
Câu 1:
Chọn A.
- Gọi O là tâm của hình bình hành ABCD. Ta có:
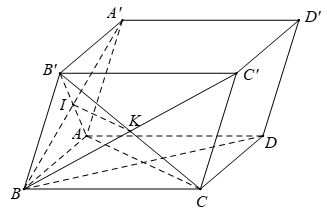
Câu 2:
Chọn D.
+) A đúng, vì:
- Tam giác B’AC có IK là đường trung bình của tam giác nên
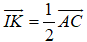
- Tứ giác ACC’A’ là hình bình hành nên
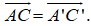
+) B đúng, vì 4 điểm I, K, C, A cùng thuộc mp(B’AC).
+) C đúng, vì:
+) D sai do giá của ba vectơ 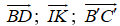
Câu 3:
Chọn B.
+) A sai vì: “nếu a và b cùng vuông góc với c thì a và b hoặc song song hoặc chéo nhau".
+) C sai do:
- Giả sử hai đường thẳng a và b chéo nhau, ta dựng đường thẳng c là đường vuông góc chung của a và b.
- Khi đó góc giữa a và c bằng với góc giữa b và c và cùng bằng 90°, nhưng hiển nhiên hai đường thẳng a và b không song song.
+) D sai do: giả sử a vuông góc với c, b song song với c, khi đó góc giữa a và c bằng 90°, còn góc giữa b và c bằng 0°.
⇒ Do đó B đúng.
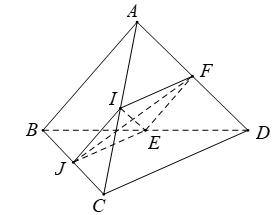
Câu 4:
Chọn D.
+) Từ giả thiết ta có:
- IJ là đường trung bình của tam giác ABC nên:
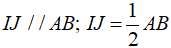
- EF là đường trung bình của tam giác ABD nên:
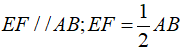
- Suy ra: tứ giác IJEF là hình bình hành (1)
- Lại có: IF là đường trung bình của tam giác ACD nên:
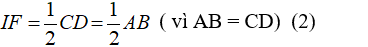
- Từ (1) và (2) suy ra: tứ giác IJEF là hình thoi.
⇒ IE ⊥ JF (tính chất hai đường chéo của hình thoi).
⇒ Do đó, góc giữa hai đường thẳng IE và JF là: 90°.
Câu 5:
Chọn D.
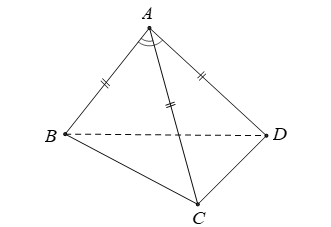
- Ta có:
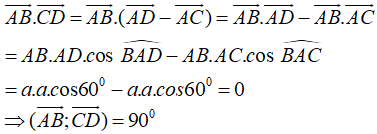
Câu 6:
Chọn D.
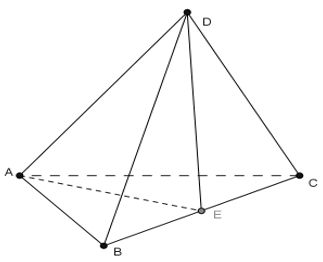
- Gọi E là trung điểm của BC.
+)Tam giác ABC có AB = AC nên tam giác ABC cân tại A có AE là đường trung tuyến nên: AE ⊥ BC.
+) Tam giác BCD có DB = DC nên tam giác DBC cân tại D có DE là đường trung tuyến nên đồng thời là đường cao: DE ⊥ BC.
+) Ta có:
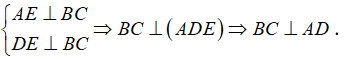
Câu 7:
Chọn A.
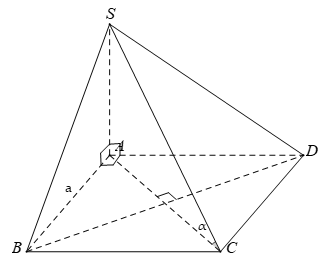
- Ta có:
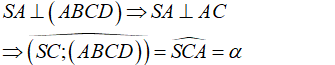
- Vì ABCD là hình vuông cạnh a:
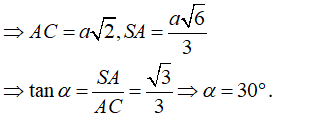
Câu 8:
Chọn A.
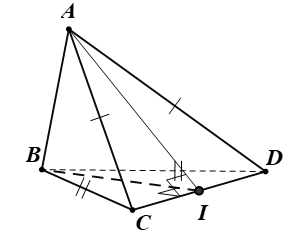
+) Tam giác BCD có BC = BD nên cân tại B: Có BI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ BI (1)
+) Tam giác ACD có AC = AD nên cân tại A: Có AI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ AI (2)
- Từ (1) và (2) ⇒ CD ⊥ (ABI) (3)
+) Vì:
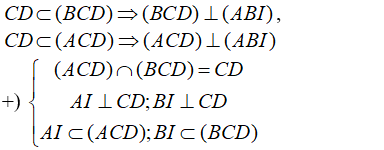
- Suy ra: góc giữa hai mặt phẳng (ACD) và (BCD) là
- Vậy: A sai.
Phần II: Tự luận
Câu 1:
Chọn C.
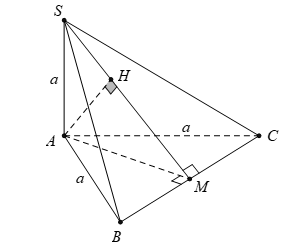
● Gọi M là trung điểm của BC ; H là hình chiếu vuông góc của A trên SM.
● Vì tam giác ABC đều nên: BC ⊥ AM.
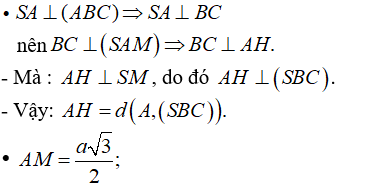
- Trong tam giác vuông SAM, đường cao AH có:
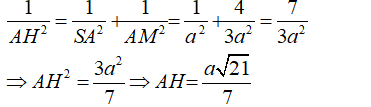
Câu 2:
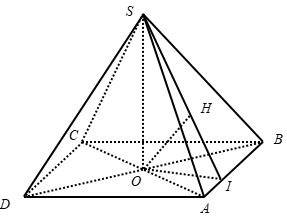
- Gọi O là giao điểm của AC và BD.
- Kẻ: OI ⊥ AB, OH ⊥ SI.
+) Ta có:
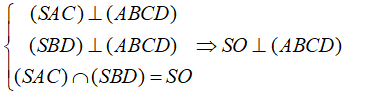
+) Ta lại có:
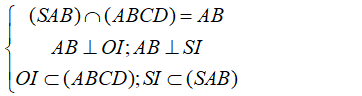
- Do đó, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng góc 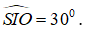
+) Khi đó: CD // AB nên CD // ( SAB).
Suy ra:

- Ta có:
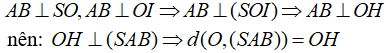
+) Tam giác ABC có BC = BA và
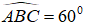
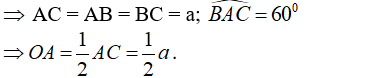
- Trong tam giác OIA có:
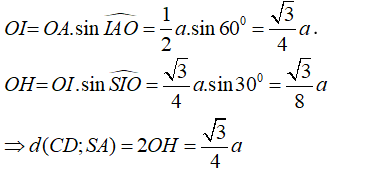
Xem thêm các đề thi Toán 11 Đại số, Hình học có đáp án hay khác:
- Đề kiểm tra 45 phút Hình học 11 Chương 2 có đáp án (Đề 1)
- Đề kiểm tra 45 phút Hình học 11 Chương 3 có đáp án (Đề 2)
- Đề kiểm tra 45 phút Hình học 11 Chương 3 có đáp án (Đề 3)
Để học tốt lớp 11 các môn học sách mới:
- Giải bài tập Lớp 11 Kết nối tri thức
- Giải bài tập Lớp 11 Chân trời sáng tạo
- Giải bài tập Lớp 11 Cánh diều
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 11 (các môn học)
- Giáo án điện tử lớp 11 (các môn học)
- Giáo án Toán 11
- Giáo án Ngữ văn 11
- Giáo án Tiếng Anh 11
- Giáo án Vật Lí 11
- Giáo án Hóa học 11
- Giáo án Sinh học 11
- Giáo án Lịch Sử 11
- Giáo án Địa Lí 11
- Giáo án KTPL 11
- Giáo án HĐTN 11
- Giáo án Tin học 11
- Giáo án Công nghệ 11
- Giáo án GDQP 11
- Đề thi lớp 11 (các môn học)
- Đề thi Ngữ Văn 11 (có đáp án)
- Chuyên đề Tiếng Việt lớp 11
- Đề cương ôn tập Văn 11
- Đề thi Toán 11 (có đáp án)
- Đề thi Toán 11 cấu trúc mới
- Đề cương ôn tập Toán 11
- Đề thi Tiếng Anh 11 (có đáp án)
- Đề thi Tiếng Anh 11 mới (có đáp án)
- Đề thi Vật Lí 11 (có đáp án)
- Đề thi Hóa học 11 (có đáp án)
- Đề thi Sinh học 11 (có đáp án)
- Đề thi Lịch Sử 11
- Đề thi Địa Lí 11 (có đáp án)
- Đề thi KTPL 11
- Đề thi Tin học 11 (có đáp án)
- Đề thi Công nghệ 11
- Đề thi GDQP 11 (có đáp án)

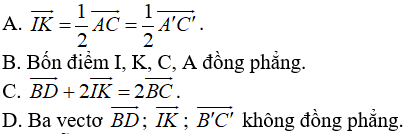
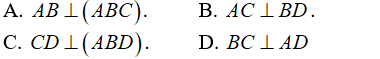
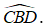


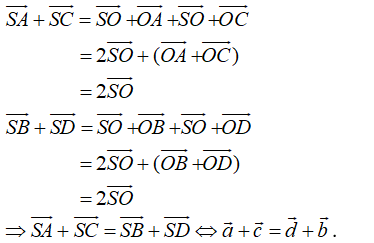
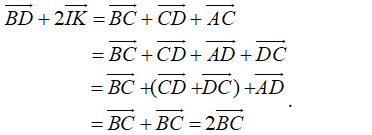
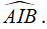



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

