Đề cương ôn tập Học kì 2 Toán 12 Cánh diều

---

---

Bộ đề cương ôn tập Học kì 2 Toán 12 Cánh diều với bài tập trắc nghiệm, tự luận đa dạng có lời giải chi tiết giúp học sinh nắm vững được kiến thức cần ôn tập để đạt điểm cao trong bài thi Toán 12 Học kì 2.

Đề cương ôn tập Học kì 2 Toán 12 Cánh diều

Xem thử

Chỉ từ 80k mua trọn bộ Đề cương ôn tập Học kì 2 Toán 12 Cánh diều có lời giải bản word trình bày đẹp mắt, dễ dàng chỉnh sửa:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Đề cương ôn tập Toán 12 Học kì 2 Cánh diều gồm hai phần: Nội dung ôn tập và Bài tập ôn luyện, trong đó:

- 112 bài tập trắc nghiệm;

- 21 bài tập tự luận;

I. Nội dung ôn tập

Chương IV. Nguyên hàm. Tích phân

Bài 1. Nguyên hàm

- Khái niệm nguyên hàm.

- Tính chất của nguyên hàm.

Bài 2. Nguyên hàm của một số hàm số sơ cấp

- Nguyên hàm của hàm số lũy thừa.

- Nguyên hàm của hàm số $y=\frac{1}{x}$.

- Nguyên hàm của hàm số lượng giác.

- Nguyên hàm của hàm số mũ.

Bài 3. Tích phân

- Định nghĩa tích phân.

- Tính chất của tích phân.

- Tích phân của một số hàm số sơ cấp.

Bài 4. Ứng dụng hình học của tích phân

- Tính diện tích hình phẳng.

- Tính thể tích hình khối.

Chương V. Phương trình mặt phẳng, đường thẳng, mặt cầu trong không gian

Bài 1. Phương trình mặt phẳng

- Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng.

- Phương trình tổng quát của mặt phẳng.

- Lập phương trình tổng quát của mặt phẳng biết một số điều kiện.

- Điều kiện song song, vuông góc của hai mặt phẳng.

- Khoảng cách từ một điểm đến một mặt phẳng.

Bài 2. Phương trình đường thẳng

- Phương trình đường thẳng.

- Vị trí tương đối của hai đường thẳng.

- Góc: góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng.

Bài 3. Phương trình mặt cầu

- Định nghĩa mặt cầu.

- Phương trình mặt cầu.

Chương VI. Một số yếu tố xác suất

Bài 1. Xác suất có điều kiện

- Định nghĩa xác suất có điều kiện.

- Sử dụng sơ đồ hình cây để tính xác suất có điều kiện.

Bài 2. Công thức xác suất toàn phần. Công thức Bayes

- Công thức xác suất toàn phần.

- Công thức Bayes.

II. Bài tập tự luyện

A. Trắc nghiệm nhiều phương án lựa chọn

Chương IV. Nguyên hàm. Tích phân

Bài 1. Nguyên hàm

Câu 1. Cho hàm số f(x) = x² + 4 . Mệnh đề nào sau đây đúng?

A. $\int f\left(x\right)dx=2x+C$.

B. $\int f\left(x\right)dx=x^2+4x+C$.

C. $\int f\left(x\right)dx=\frac{x^3}{3}+4x+C$.

D. $\int f\left(x\right)dx=x^3+4x+C$.

Câu 2. Mệnh đề nào sau đây là sai?

A. $\int x^{\alpha }dx=\alpha x^{\alpha -1}+C$.

B. $\int dx=x+C$.

C. $\int 0dx=C$.

D. $\int \frac{1}{x}dx=\ln \left|x\right|+C$.

Câu 3. Họ nguyên hàm của hàm số f(x) = 3x² + 2x + 5 là:

A. $\int f\left(x\right)dx=x^3+x^2+5$.

B. $\int f\left(x\right)dx=x^3+x^2+5x+C$.

C. $\int f\left(x\right)dx=x^3+x^2+C$.

D. $\int f\left(x\right)dx=6x+2+C$.

Câu 4. Nguyên hàm của hàm số f(x) = $\frac{1}{3}{x}^3-2x^2+x-2024$ là

A. $\frac{1}{12}{x}^4-\frac{2}{3}{x}^3+\frac{x^2}{2}+C$.

B. $\frac{1}{9}{x}^4-\frac{2}{3}{x}^3+\frac{x^2}{2}-2024x+C$.

C. $\frac{1}{12}{x}^4-\frac{2}{3}{x}^3+\frac{x^2}{2}-2024x+C$.

D. $\frac{1}{9}{x}^4+\frac{2}{3}{x}^3-\frac{x^2}{2}-2024x+C$.

Câu 5. Tìm nguyên F(x) của hàm số f(x) = (x + 1)(x + 2))x + 3)?

A. $F\left(x\right)\text{\hspace{0.17em}}=\frac{x^4}{4}-6x^3+\frac{11}{2}{x}^2-6x+C$.

B. $F\left(x\right)\text{\hspace{0.17em}}=x^4+6x^3+11x^2+6x+C$.

C. $F\left(x\right)\text{\hspace{0.17em}}=\frac{x^4}{4}+2x^3+\frac{11}{2}{x}^2+6x+C$.

D. $F\left(x\right)\text{\hspace{0.17em}}=x^3+6x^2+11x^2+6x+C$.

Câu 6. Tìm nguyên hàm của hàm số f(x) = (5x + 3)⁵.

A. (5x + 3)⁶ + C.

B. (5x + 3)⁴ + C.

C. $\frac{{(5x+3)}^6}{30}+C$.

D. $\frac{{(5x+3)}^4}{30}+C$.

Câu 7. Gọi F(x) là một nguyên hàm của hàm số $f\left(x\right)={(x^2+1)}^2$ thỏa $F\left(1\right)=\frac{28}{15}$. Tính T = 5F(6) - 30F(4) + 18.

A. T = 8526.

B. T = 1000.

C. T = 7544.

D. T = 982.

Câu 8. Gọi F(x) là một nguyên hàm của hàm số f(x) = (2x - 3)² thỏa $F\left(0\right)=\frac{1}{3}$. Tính giá trị của biểu thức T = ${\log }_2\left[3F\left(1\right)-2F\left(2\right)\right]$.

A. T = 2.

B. T = 4.

C. T = 10.

D. T = -4.

Câu 9. Trong một đợt xả lũ, nhà máy thủy điện đã xả lũ trong 40 phút với tốc độ lưu lượng nước tại thời điểm t giây là h'(t) = 10t + 500 (m³/s). Hỏi sau thời gian xả lũ trên thì hồ thoát nước của nhà máy đã thoát đi một lượng nước là bao nhiêu?

A. 5.10⁴ (m³).

B. 4.10⁶ (m³).

C. 3.10⁷ (m³).

D. 6.10⁶ (m³).

Câu 10. Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho h'(t) = 3at² + bt (m³/s) và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là 150 m³. Sau 10 giây thì thể tích nước trong bể là 1100 m³. Hỏi thể tích nước trong bể sau khi bơm được 20 giây là bao nhiêu.

A. 8400 m³.

B. 840 m³.

C. 6400 m³.

D. 4200 m³.

................................

................................

................................

C. Trắc nghiệm trả lời ngắn

Chương IV. Nguyên hàm. Tích phân

Câu 1. Biết F(x) là một nguyên hàm của hàm số f(x) = e^2x và F(0) = 0. Giá trị của F(ln 3) bằng bao nhiêu?

Câu 2. Cho hàm số f(x) = $\left\{\begin{array}{l}2x+3\text{\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}khi\hspace{0.33em}}x\ge 1\\ 3x^2+2\text{\hspace{0.33em}khi\hspace{0.33em}}x<1\end{array}\right.$. Giả sử F(x) là nguyên hàm của hàm số f(x) trên ℝ thỏa mãn F(0) = 2. Giá trị của F(-1) + 2F(2) bằng bao nhiêu?

Câu 3. Biết $\underset{1}{\overset{3}{\int }}\frac{x+2}{x}dx=a+b\ln c$, với $a,b,c\in \mathbb{Z},c<9$. Tính tổng S = a + b + c.

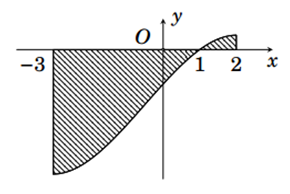
Câu 4. Tính diện tích phần hình phẳng gạch chéo (tam giác cong OAB) trong hình vẽ bên (kết quả làm tròn đến hàng phần trăm).

Câu 5. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), trục hoành và hai đường thẳng x = -3, x = 2 (như hình vẽ bên). Đặt $-5=\underset{-3}{\overset{1}{\int }}f\left(x\right)\text{\hspace{0.17em}d}x$, $2=\underset{1}{\overset{2}{\int }}f\left(x\right)\text{\hspace{0.17em}d}x$. Tính S.

 

Câu 6. Cắt một vật thể (T) bởi hai mặt phẳng vuông góc với trục Ox tại x = 0 và x = 2. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 2) cắt vật thể theo mặt cắt là một hình vuông có cạnh bằng $\sqrt{x^3}$. Tính thể tích vật thể (T).

Câu 7. Cho hình phẳng D giới hạn bởi đường cong $y=\sqrt{2+\sin x}$, trục hoành và các đường thẳng x = 0, x = π. Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu? (lấy π = 3,14) (kết quả làm tròn đến hàng đơn vị).

................................

................................

................................

Xem thử

Xem thêm đề cương ôn tập Toán 12 Chân trời sáng tạo hay khác:

• Đề cương ôn tập Giữa kì 1 Toán 12 Cánh diều

• Đề cương ôn tập Học kì 1 Toán 12 Cánh diều

• Đề cương ôn tập Giữa kì 2 Toán 12 Cánh diều

---

---

---