Đề thi Học kì 1 Toán lớp 10 năm 2024 có ma trận (8 đề)

Đề thi Học kì 1 Toán lớp 10 năm 2024 có ma trận (8 đề)

Tuyển chọn Đề thi Học kì 1 Toán lớp 10 năm 2024 có ma trận (8 đề) chọn lọc được các Giáo viên nhiều năm kinh nghiệm biên soạn và sưu tầm từ Đề thi Toán 10 của các trường THPT. Hi vọng bộ đề thi này sẽ giúp học sinh ôn tập và đạt kết quả cao trong các bài thi Học kì 1 môn Toán lớp 10.

A. MA TRẬN ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I

Cấp độ Chủ đề	Nhận biết	Thông hiểu	Vận dụng	Cộng
1. Hàm số bậc nhất và bậc hai	Nhận biết được cách tìm TXĐ của hàm số đơn giản.	Hiểu được tọa độ đỉnh parabol và điểm thuộc đồ thị
Số câu (ý) Số điểm Tỷ lệ %	1 1đ	1 1đ		2 2,0đ =20%
2. Phương trình	Nhận biết được cách giải phương trình chứa ẩn ở mẫu và chứa ẩn trong căn đơn giản.		Biết vận dụng định lý Viet vào tìm nghiệm pt bậc hai thỏa mãn biểu thức đối xứng các nghiệm. Vận dụng pp đặt ẩn phụ, pp liên hợp giải pt vô tỷ.
Số câu (ý) Số điểm Tỷ lệ %	2 2,5đ		2 2đ	4 4,5đ =45%
3. Véc tơ – Tích vô hướng của hai Véc tơ.		Hiểu được việc xét sự thẳng hàng ba điểm và tính được tích vô hương của hai véc tơ khi biết tọa độ các điểm	Vận dụng được TVH của hai véc tơ và các tính chất vào tìm tọa độ các điểm thỏa mãn tính chất hình học cho trước.
Số câu (ý) Số điểm  Tỷ lệ		2 2,25đ	1 1,25đ	3 3,5đ =35%
Số câu (ý) Số điểm Tỷ lệ	3 3,5đ =35%	3 3,25đ =32,5%	3 3,25đ =32,5%	9 10,0đ =100%

B. ĐỀ THI:

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

Bài 1. Cho hàm số f(x) = 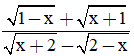 . Xét tính chẵn, lẻ của hàm số f.

Bài 2. Giải phương trình

a)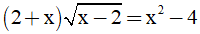      

2) |x² - 4x| = 5 -2x

Bài 3. Cho hàm số: y = x2 – 2x – 3  đồ thị là (P).

1) Lập bảng biến thiên và vẽ đồ thị của hàm số trên.

2) Dựa vào đồ thị (P) tìm m sao cho phương trình 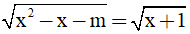 có nghiệm.

Bài 4. Cho hệ phương trình 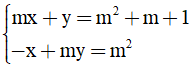 (m là tham số).

Xác định m sao cho hệ có nghiệm (x;y) thỏa mãn x² + y² đạt giá trị nhỏ nhất.

Bài 5. Trong mặt phẳng tọa độ Oxy cho các điểm  A(0;1), B(1;3), C(-2;2):

a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông cân. Tính diện tích tam giác ABC. Xác định tâm đường tròn ngoại tiếp tam giác ABC.

b) Đặt 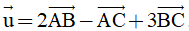. Tính .

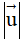c) Tìm tọa độ điểm M ∈ Ox thỏa mãn 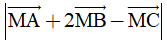 bé nhất.

Bài 6. Giải phương trình: 4x² = 5x - 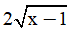 - 1

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

I. Phần trắc nghiệm

Câu 1. Tìm mệnh đề phủ định của mệnh đề: ∀x ∈ ℝ, x² + x + 5 > 0 .

A. ∃x ∈ ℝ, x² + x + 5 < 0.    

B. ∀x ∈ ℝ, x² + x + 5 < 0.

C. ∀x ∈ ℝ, x² + x + 5 ≤ 0.    

D. ∃x ∈ ℝ, x² + x + 5 ≤ 0.

Câu 2. Cho tập hợp P. Tìm mệnh đề sai trong các mệnh đề sau?

A. P ⊂ P.    

B. ∅ ⊂ P.           

C. P ∈ .                      

D. P ∈ P.

Câu 3. Tập hợp nào sau đây có đúng một tập hợp con?

A. ∅.                                 

B. d: y = 2k - 3.    

C. {∅}.                                       

D. {1; ∅}.

Câu 4. TXĐ của hàm số y = 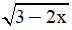 là :

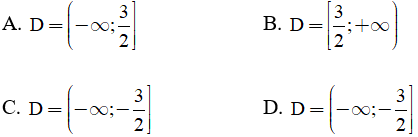
Câu 5. Chọn mệnh đề đúng

A. Hàm số y = x⁴ - 2x² - 3 là hàm số không lẻ không chẵn      

B. Hàm số 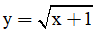 là hàm số chẵn

C. Hàm số y = x⁴ - 2x² - 3 là hàm số lẻ                                

D. Hàm số y = x⁴ - 2x² - 3 là hàm số chẵn

Câu 6. Cho hàm số y = -2x + 3. Trong các điểm sau đây, điểm nào thuộc đồ thị hàm số?

A. M₁(3; 0)   

B. M₄(2; -1)  

C. M₂(-1; 1)     

D. M₂(1; -1)      

Câu 7. Biết đồ thị hàm số y = ax + b là đường thẳng đi qua K(5; -4) và vuông góc với đường thẳng y = x + 4. Hỏi A = a = 2b bằng

A. 0    

B. -2    

C. 1    

D. -1

Câu 8. Tọa độ giao điểm của đường thẳng y = x - 1 và (P) y = x² - 2x -1 là:

A. (0; 1), (3; 2)     

B. (1; -1), (3; 2)     

C. (0; -1), (-3; 2)     

D. (0; -1), (3; 2) 

Câu 9. Đồ thị của hàm số nào dưới đây đi qua điểm M(1; 2)?

A. y = 2x² - 4x + 4     

B. y = 2x² - 3x + 4     

C. y = 2x² + x + 4     

D. y = 2x² + 4x - 3 

Câu 10. Cho hàm số y = x² - 2x + 2. Khẳng định nào sau đúng?

A. Đồ thị của hàm số có đỉnh I(1; -4).    

B. Đồ thị hàm số có tung độ đỉnh I(-1; 3).

C. Đồ thị hàm số có trục đối xứng: x = 1.    

D. Đồ thị hàm số có trục đối xứng: x = -1 .

Câu 11. Cho hàm số y = f(x) = x² - 2x + 2. Mệnh đề nào sau đây đúng?

A. Nghịch biến trong (-∞; -1)    

B. Đồng biến trong (3; +∞).

C. Đồng biến trong (1; +∞)    

D. Nghịch biến trong (1; +∞)

Câu 12. Hình vẽ bên là đồ thị của hàm số nào?

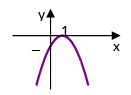
A. y = – x² + 2x;    

B. y = – x² + 2x – 1;

C. y = x² – 2x;        

D. y = x² – 2x + 1.                       

Câu 13. Cho A = (-∞; m + 1); B = (-1; +∞). Điều kiện để (A ∪ B) = ℝ là

A. m > -1 .    

B. m ≥ -2.    

C. m ≥ 0.   

D. m > -2.

Câu 14. Với vectơ 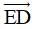 (khác vectơ không) thì độ dài đoạn thẳng ED được gọi là:

A. Phương của vectơ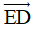      

B. Hướng của vectơ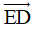  

C. Giá của vectơ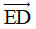      

D. Độ dài của vectơ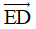  

Câu 15. Cho hình chữ nhật ABCD biết AB = 4a và AD = 3a thì độ dài ?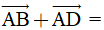

A. 7a.                             

B. 6a.                                  

C. 2a√3.                   

D. 5a.

Câu 16. Cho hình bình hành ABCD tâm O. Đẳng thức nào sau đây đúng?

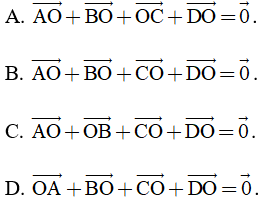
Câu 17. Cho G là trọng tâm tam giác ABC vuông, cạnh huyền BC = 12. Độ dài vectơ 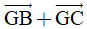 bằng:

A. 2.                               

B. 8.                                      

C. 6.                               

D. 4.

Câu 18. Chọn phát biểu sai?

A. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi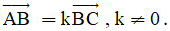

B. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi .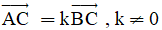

C. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi .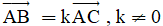

D. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi .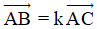

Câu 19. Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là sai:

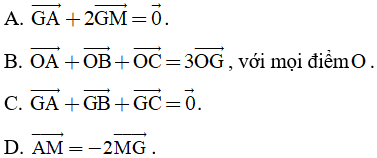
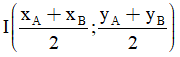Câu 20. Cho tam giác ABC. Gọi là điểm trên cạnh sao cho . Khi đó

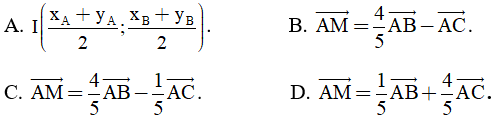
II. Phần tự luận

Câu 1: (2 điểm) Cho hàm số y = - 3x2 + 3x + 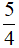. Có đồ thị (C). Xác định tọa độ đỉnh và trục đối xứng (C)

Câu 2: (1 điểm) Tìm Parabol (P) : y = ax² + bx + c biết (P) qua A(0; 2) và có đỉnh S(1; 1)

Câu 3: (1,5 điểm) Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của AB và CD; I và J là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: 

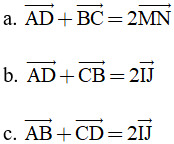
Câu 4: (1,5 điểm) Giải phương trình:

a) ;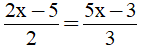

b) |2x – 3| = |x + 1|;

c)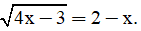  

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

I. Phần trắc nghiệm

Câu 1: Trong hệ trục tọa đ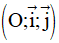ộ , cho 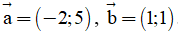. Tính .

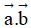Câu 2: Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. y = x².                        

B. y = x³.                         

C. y = x⁴.                        

D. y = |x|.

Câu 3: Cho mệnh đề chứa biến P(x): ''x² = 4, x ∈ ℝ'' Chỉ ra mệnh đề đúng trong các mệnh đề sau

A. P(4).                           

B. P(-1).                         

C. P(-3).                         

D. P(-2).

Câu 4:   Cho A = , B = . Chọn kết quả đúng trong các kết quả sau :

A. A ∩ B = {1; 3; 5}.           

B. A ∩ B = {3; 5; 7; 9}.       

C. A ∩ B = {1; 3; 5; 7; 9}.     

D. A ∩ B = {3; 5}.

Câu 5. Cho A = (-∞; 5], B = (0; +∞). Tìm A ∩ B.

A. A ∩ B = [0; 5)           

B. A ∩ B = (0; 5)          

C. A ∩ B = (-∞; +∞) 

D. A ∩ B = (0; 5]

Câu 6. Xác định a để hàm số y = (1 -2a)x - 1 đồng biến trên ℝ

A. [-1; 4)                   

B. a ≥ 1                       

C. a <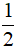                      

D. a >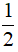

Câu 7: Cho hàm số bậc hai y = ax² + bx + c, (a ≠ 0), có đồ thị là parabol (P). Gọi I là đỉnh của parabol (P).Tọa độ đỉnh I được xác định bởi công thức

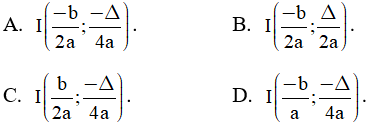
Câu 8: Cho hàm số bậc hai y = x² - 2x + 3 có đồ thị là parabol (P). Chọn khẳng định đúng trong các khẳng định sau

A. (P) đi qua gốc tọa độ.                                    

B. (P) quay bề lõm xuống dưới.                          

C. (P) có trục đối xứng là x = 2.                        

D. (P) cắt trục tung tại điểm M(0; 3).

Câu 9. Điều kiện xác định của phương trình 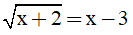 là :

A. x ≥ 3.                    

B. x > -2.                  

C. x ≥ -2.                 

D. -2 ≤ x ≤ 3.

Câu 10. Với m = -1 thì phương trình (1 - m²)x = m -1

A. Vô nghiệm. 

B. Có nghiệm x =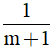

C. Nghiệm đúng ∀x ∈ ℝ.                              

D. Có 2 nghiệm phân biệt.

Câu 11: Nghiệm của hệ phương trình 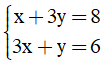có dạng (x₀, y₀). Tính T = x₀ + y₀.

A. T = 6                      

B. T = 2                     

C. T =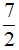                        

D. T =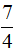

Câu 12. Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn:

 

Câu 13. Hệ phương trình 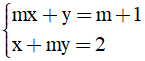có nghiệm duy nhất khi:

 

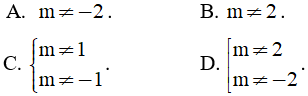
Câu 14: Cho ba điểm M, N, P bất kỳ thỏa mãn đẳng thức 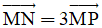. Chọn khẳng định sai trong các khẳng định sau

A. 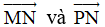 cùng phương.                              

B. Điểm P nằm giữa hai điểm M và N.             

C. Ba điểm M, N, P là 3 đỉnh của một tam giác.                                 

D. Ba điểm M, N, P thẳng hàng.

Câu 15. Trong mặt phẳng toạ độ Oxy, Cho M thoả 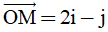. Toạ độ điểm M là:

A. (2; -1)                    

B. (1; 2)                        

C. (-1; 2)                    

D. (2; 1)

Câu 16. Cho tam giác ABC đều. Góc giữa hai vectơ 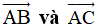 bằng:

A. 150⁰                      

B. 60⁰                   

C. 120⁰                       

D. 30⁰ 

Câu 17: Cho A = (-∞; 2) và B = (-3; 6]. Khẳng định nào sau đây đúng ?

A. A\B = (-∞; -3)   

B. A ∪ B = (-∞; 6]     

C. A ∩ B = [-3; 2)       

D. B \ A = (2; 6]

Câu 18:  Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. ''∀x ∈ ℝ, x ⋮ 6 => x ⋮ 3''.                                     

B. ''∀x ∈ ℝ, x ⋮ 3 => x ⋮ 9''.   

C.  ''∀x ∈ ℝ, x ⋮ 8 => x ⋮ 4''.                                     

D. ''∀x ∈ ℝ, x ⋮ 10 => x ⋮ 5''.

Câu 19. Với điều kiện nào của tham số m thì phương trình có nghiệm (3m² - 4)x - 1 = m -x thực duy nhất?

A. m ≠ 0.                   

B. m ≠ ±1                 

C. m ≠ -1.                 

D. m ≠ 1.

Câu 20. Cho a> 0, b > 0, c < 0. Khẳng định nào sau đây đúng?

A.  Phương trình ax² + bx + c = 0 có một nghiệm duy nhất.

B.  Phương trình ax² + bx + c = 0 có hai nghiệm dương phân biệt.

C.  Phương trình ax² + bx + c = 0 có hai nghiệm âm phân biệt.

D.  Phương trình ax² + bx + c = 0 có hai nghiệm trái dấu.

II. PHẦN TỰ LUẬN 

Câu 1. (2 ĐIỂM)

a) Giải phương trình sau: |4x + 5| = |x - 3| 

b) Cho phương trình: x² - 2x + 3 - (m + 1)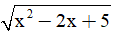 - m = 0. Tìm m để phương trình có nghiệm.

Câu 2. (2 ĐIỂM) Cho tam giác có A(1; -2), B(4; -1), C(-1; 4)

a) Tìm tọa độ các vectơ .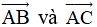      

b) Chứng minh rằng tam giác ABC là tam giác vuông.

Câu 3. (1 ĐIỂM) Lập bảng biến thiên và vẽ đồ thị của hàm số y = x² - x + 3.

                                                   

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 4)

I. PHẦN TRẮC NGHIỆM (4 ĐIỂM)

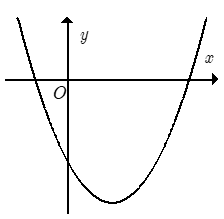
Câu 1. Cho hàm số thì đồ thị (P) của hàm số là hình nào trong các hình sau :     

                                                                   

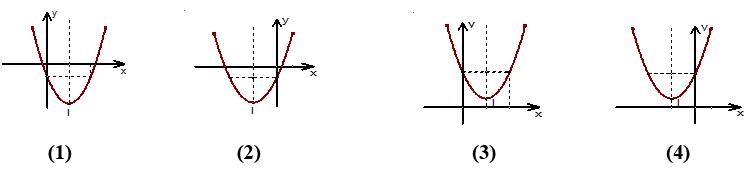
A. Hình (4)                   B. Hình (2)               C. Hình (3)               D. Hình (1)

Câu 2. Xác định m để 3 đường thẳng d₁: y = 3 – x; d₂: y = 3x + 5 và d₃: y = (3m – 1)x + m đồng quy.

A. m = 3               B. m = –3              C. m = 6               D. m = –6

Câu 3. Tìm giá trị của m để hàm số y = x² + 2(m – 1)x + m² – 4 có giá trị nhỏ nhất bằng 5.

A. m = 1               B. m = 2                C. m = 4               D. m = 5

Câu 4. Tìm giá trị của m để đồ thị hàm số y = –mx + 2m (m ≠ 0) lần lượt cắt Ox, Oy tại A, B thỏa mãn tam giác OAB có diện tích bằng 12.

A. m = ±6             B. m = ±3              C. m = 3 ; m = 6    D. m = –3 ; m = –6

Câu 5. Số nghiệm của phương trình 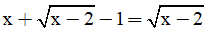 là:

A. 2                            

B. 0                            

C. 3                            

D. 1

Câu 6. Nghiệm của hệ phương trình 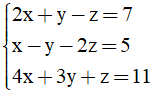 là:

A. (-1; 3; 0) .               

B. (-1; 0: 3).                

C. (-3; -1; 0).             

D. (3; 0; -1)

Câu 7: Một số tự nhiên có hai chữ số. Nếu lấy số đó trừ đi hai lần tổng các chữ số của nó thì được kết quả là 51. Nếu lấy hai lần chữ số hàng chục cộng với ba lần chữ số hàng đơn vị thì được kết quả là 29. Hỏi số tự nhiên ấy có giá trị thuộc khoảng nào trong các khoảng sau?

A. (80; 90).                       

B. (70; 80).                       

C. (50; 60).                       

D. (60; 70).

Câu 8: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-1; 3), B(4; 2), C(3; 5). Tìm tọa độ điểm D thỏa mãn .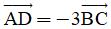

A. D(6; -2).                     

B. D(6; 2).                        

C. D(2; 6).                        

D. D(2; -6).

Câu 9: Trong mặt phẳng tọa độ Oxy, cho điểm B(2; 4). Tính tọa độ điểm trung điểm I của OB:

A. I(0; 4).                         

B. I(1; 2).                          

C. I(2; 4).                         

D. I(2; 0).

Câu 10: Tam giác ABC vuông ở A và có góc ∠C = 40⁰. Tính góc giữa 2 véctơ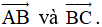

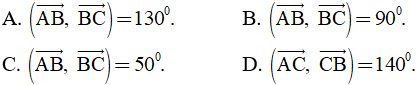
Câu 11. Cho hàm số y = x² - 4x + 2. Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên khoảng (2; +∞).     

B. Hàm số đồng biến trên khoảng (-∞; 2).

C. Hàm số nghịch biến trên khoảng (-∞; -2).      

D. Hàm số đồng biến trên khoảng (-2; +∞).

Câu 12. Cho hàm số y = ax² + bx + c có đồ thị như hình vẽ dưới đây. Chọn khẳng định đúng trong các khẳng định sau: 

A. a > 0; b < 0, c > 0                                   

B. a < 0; b < 0, c > 0 

C. a > 0; b < 0, c < 0                                  

D. a > 0; b > 0, c > 0

Câu 13: Cho đường thẳng d: y = 2x + 2020, đường thẳng d' song song với đường thẳng d và đi qua điểm M(0; 3). Phương trình đường thẳng d' là :

A. y = 2x + 3.                    

B. y = -2x + 3.               

C. y = 2x - 3.                  

D. y = -2x - 3.

Câu 14. A={0; 1; 2; 3}, B={x ∈ N| (x + 1)(x + 2)(x - 1) = 0 và E = B\A. Khẳng định nào sau đây đúng? 

A. E = {0; 2; 3}

B. E = {1}                    

C. E = ∅. 

D. E = {-2;1}. 

Câu 15: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(-4; 1), B(2; 4), C(2; -2). Tìm tọa độ điểm D sao cho C là trọng tâm tam giác ABD.

A. D(-8; -11).                 

B. D(0; -1).                     

C. D(0; 1).                        

D. D(8; -11).

Câu 16: Cho 2 vectơ 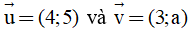. Tính a để góc giữa hai véc tơ bằng 90⁰ ?

Câu 17. Trong mặt phẳng Oxy, cho A(-2; 1), B(1; 7). Tọa độ điểm E trên trục  mà A, B, E thẳng hàng là:

A. E(0; -3)                 

B. E(0; 3)                     

C. E(0; 5)                     

D. E( -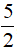; 0)

Câu 18. Với m ∈ [a, b] thì hệ phương trình 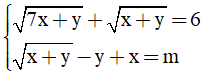 có nghiệm . Tính giá trị của biểu thức T = a + 4b

A. T = 16                     

B. T = 6                       

C. T = 8                       

D. T = 18

Câu 19. Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi AH là đường cao của tam giác ABC Tính tích vô hướng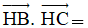

A. -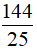                   

B. -25                       

C. 25                         

D.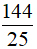

Câu 20: Cho hai điểm A(1; 0) và B(0; -2).Tọa độ điểm D sao cho  là

A. D(-3; 4).                B. D(3; 4).                   C. D(-1; -4).          D. D(3; -4).

II. PHẦN TỰ LUẬN (6 ĐIỂM)

Bài 1. (1,5 điểm) Giải các phương trình sau

a)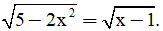

b) |2x² - x| - 2x = 5

Bài 2. (1 điểm) Xác định parabol (P): y = x² + bx + c biết (P) đi qua điểm A(2; 3) và có trục đối xứng x = 1 

Bài 3. (2,5 điểm) Trong mặt phẳng Oxy cho ba điểm A(-2; 1), B(-1; 4), C(4; -1)

a) Tính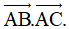

b) Tính chu vi tam giác ABC.

c) Tính diện tích tam giác ABC.

d) Tìm tọa độ điểm M sao cho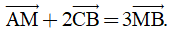

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 5)

I. Phần trắc nghiệm (4 điểm)

Câu 1: Cho tam giác ABC có trọng tâm là G(–1; 1). Biết A(6; 1), B(–3; 5) .Tọa độ đỉnh C là

A. C(6; -3).        B. C(6; 3).       C. C(-6; -3).       D. C(-6; 3).

Câu 2: Cho parabol (P): y = ax² + bx + c. Biết (P) đi qua các điểm A(0; 1), B(1; -1) và C(-1; 1). Khi đó 2a + b + c  bằng

A. -1.           B. 0.            C. 1.             D. 2.

Câu 3: Phương trình sau có bao nhiêu nghiệm |x - 2| = 2 - x 

A. 2.            B. 1.            C. 0.             D. Vô số.

Câu 4: Tập nghiệm của phương trình: 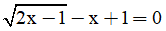 là

A. {2 - √2, 2 + √2} B. {2 - √2} C. {2 + √2}         D. ∅ 

Câu 5: Cho các vectơ 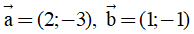. Khẳng định nào sau đây là đúng?   .

Câu 6: Cho tập hợp E = {x ∈ ℝ|(x3 - 9x)(x2 - 2x) = 0}, E được viết theo kiểu liệt kê là

A. E = {0; 2; 3; 9} . B. E = {2; 3}. C. E = {0; 2; 3}. D. E = {-3; 0; 2; 3}.

Câu 7: Hàm số nào sau đây là hàm số chẵn

A. y = x² – x⁴ + 2            B. y = x² + 2x - 4             C. y = x³ + 2x           D. y = x + 2.

Câu 8: Cho (P): y = x² - 2x - 3. Tìm câu khẳng định đúng.

A. Hàm số đồng biến trên (-∞; 1) và nghịch biến trên (1; +∞).

B. Hàm số đồng biến trên (-∞; -4) và nghịch biến trên (-4; +∞).

C. Hàm số đồng biến trên (-4; +∞) và nghịch biến trên (-∞; -4).

D. Hàm số đồng biến trên (1; +∞) và nghịch biến trên (-∞; 1).

Câu 9: Số nghiệm của phương trình: 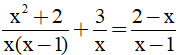 là

A. 3.        B. 1.         C. 2.         D. 0 .

Câu 10: Khẳng định nào sai khi nói về hàm số y = - x + 1:

A. Hàm số đồng biến trên ℝ.           

B. Đường thẳng có hệ số góc bằng -1.

C. Đồ thị là đường thẳng luôn cắt trục Ox và Oy.      

D. Hàm số nghịch biến trên ℝ.

Câu 11: Đồ thị của hàm số y = x³ - 2x + 1 đi qua điểm nào sau đây:

A. (1; 2).    B. (-1; 0).    C. (-1; -2).    D. (1; 0).

Câu 12: Khẳng định nào đúng khi biết I là trung điểm của đoạn thẳng MN?

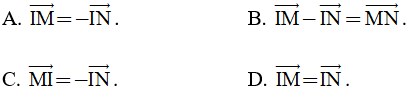
Câu 13: Cho A(2; -3), B(4; 1). Tọa độ điểm M trên đường thẳng x = -3 để A, B, M thẳng hàng là

A. M(3; 13).           B. M(3; -13).          C. M(-3; -13).            D. M(-3; 13).

Câu 14: Trong mặt phẳng tọa độ Oxy cho A(10; 8), B(4; 2). Tọa độ của vectơ 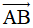 là

A. (7; 5).    B. (14; 10).    C. (6; 6).    D. (-6; -6).

Câu 15: Cho A(1; -1), B(4; 1), C(1; 3). Tìm tọa độ điểm D để tứ giác ABDC là hình bình hành

A. D(4; 5).    B. D(4; -5).    C. D(-4; -5).    D. D(-4; 5).

Câu 16: Tập xác định của hàm số 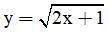 là

Câu 17: Cho hai điểm A(1; 0) và B(0; -2).Tọa độ điểm D sao cho 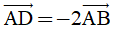 là

A. D(-3; 4).    B. D(3; 4).    C. D(-1; -4).    D. D(3; -4).

Câu 18: Hệ phương trình 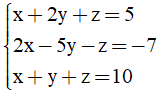 có  nghiệm là

Câu 19: Cho tập hợp A = . Hãy viết lại tập hợp A dưới kí hiệu khoảng, nửa khoảng, đoạn.

A. A = (-∞; -1).        B. A = (-1; +∞).        C. A = (1; +∞).        D. A = [-1; +∞).

Câu 20: Cho tập hợp số sau M = (-3; 2]; N = (1; 5]. Tập hợp M ∩ N là

A. (-1; 2).           B. (1; 2].            C. (-3; 5].            D. (-3; 1].

B. Phần tự luận (6.0 điểm)

Bài 1: (2.0 điểm) Lập bảng biến thiên và vẽ đồ thị hàm số y = x² - 2x - 3.

Bài 2: (1.5 điểm) Giải phương trình sau: 

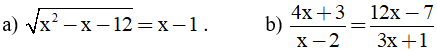
Bài 3: (2.0 điểm) Trong mp Oxy  cho A(1; 3); B(4; -2); C(3; -5) . 

a) Tìm tọa độ điểm D sao cho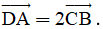

b) Tìm tọa độ điểm K sao cho C là trọng tâm của tam giác ABK. 

Bài 4: (0.5 điểm) Giải phương trình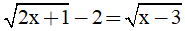  

                                                   

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 6)

A. PHẦN TRẮC NGHIỆM: (4 điểm)

Câu 1: Trong mặt phẳng tọa độ Oxy cho hai vectơ 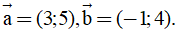. Tìm tọa độ của vectơ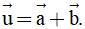  

Câu 2: Cho 3 điểm phân biệt A, B, C. Đẳng thức nào sau đây là đúng ?

Câu 3: Trong mặt phẳng Oxy, cho A(-2; 4), B(1; 5). Tìm tọa độ điểm E sao cho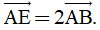

A. E(8; 6)                    B. E(4; 6)                 C. E(4; -2)             D. E(8; -2)

Câu 4: Cho parabol (P): y = ax² + bx + c có đồ thị như hình bên. Phương trình của parabol này có

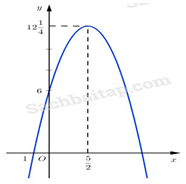
A. a < 0, b > 0, c > 0.    

B. a < 0, b < 0, c > 0.    

C. a < 0, b < 0, c < 0.    

D. a > 0, b > 0, c > 0.

Câu 5: Tìm tọa độ đỉnh parabol y = -x² + 6x -5.

A. I(0; -5).        B. I(3; 4).         C. I(1; 0).          D. I(1; 5).

Câu 6: Tìm nghiệm của hệ phương trình .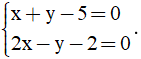

A. (2; 2).          B. (-3; -2).         C. (2; 3).        D. (3; 2) 

Câu 7: Cho hình chữ nhật ABCD có AD = 7, CD = 3, khi đó 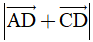 bằng:

A. 4.                B. 10.                C. 58.            D. √58.

Câu 8: Cho lục giác đều ABCDEF với O là tâm của lục giác đều. Số các vectơ bằng 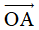 có điểm đầu và điểm cuối là đỉnh của lục giác:

A. 2.               B. 8.                   C. 6.             D. 3.

Câu 9: Phương trình 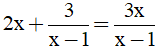 có bao nhiêu nghiệm?

A. 2.               B. 0                   C. 1.              D. 3.

Câu 10: Cho tập hợp A = {3; 4; 7; 8}, B = {4; 5; 6; 7}. Xác định tập hợp A\B.

A. {4; 7}. B. {5; 6}. C. {3; 8}. D. {3; 4; 5; 6; 7; 8}.

Câu 11: Đồ thị hàm số y = ax + b đi qua điểm M(1; 4), N(2; 7). Giá trị a + b là:

A. 4.              B. 6.                   C. 5.              D. 3.

Câu 12: Tập nghiệm của phương trình .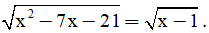

A. S = ∅.       B. S = {-2}.         C. S = {10}.     D. S = {-2; 10}.

Câu 13: Cho ∆ABC có trọng tâm G, I là trung điểm của đoạn thẳng BC. Đẳng thức nào sau đây SAI ?

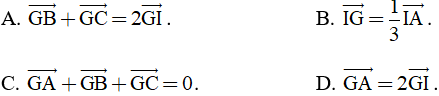
Câu 14: Trong mặt phẳng Oxy, cho A(1; 3), B(2; -5). Tìm tọa độ của vectơ .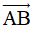

Câu 15: Cho hàm số y = -x² + 2x + 3 có đồ thị (P). Chọn khẳng định SAI ?.

A. Đồ thị nhận đường thẳng x = -1 làm trục đối xứng.

B. Hàm số đồng biến trên (-∞; 1) và nghịch biến trên (1; +∞).

C. Parabol (P) luôn đi qua điểm A(0; 3)

D. Parabol (P) có tọa độ đỉnh I(1; 4).

Câu 16: Cho tập hợp A = (2; 5), B = [-4; 3). Xác định tập hợp A ∪ B.

A. [-4; 5).           B. (3; 5).           C. [-4; 2).            D. (2; 3).

Câu 17: Với giá trị nào của m thì phương trình x² - (2m + 1)x + m² + 3 = 0 có hai nghiệm phân biệt?

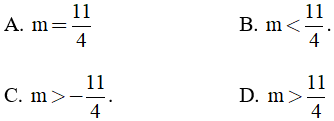
Câu 18: Trong mặt phẳng Oxy, cho A(-2; 4), B(1; 3), C(-5; 2). Tìm tọa độ trọng tâm G của ΔABC.

A. G(-6; 9).            B. 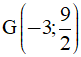.           C. G(-3; 2).              D. G(-2; 3).

Câu 19: Cho tập hợp E = {x ∈ ℤ|(x - 5)(x2 - 4x + 3) = 0}. Viết tập hợp E bằng cách liệt kê phần tử.

A. E = {-5; 1; 3}.    B. E = {1; 3; 5}.       C. E = {-3; -1; 5}.    D. E = {-5; -3; -1}.

Câu 20: Tìm tập xác định của hàm số .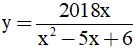

A. (2; 3).    B. D = R\{2; 3}.    C. D = {2; 3}.    D. D = R\{2018}.

B. PHẦN TỰ LUẬN: (6 điểm)

Bài 1. (2.0 điểm) Lập bảng biến thiên và vẽ đồ thị hàm số y = x² + 2x - 3 

Bài 2. (1.0 điểm) Giải phương trình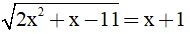  

Bài 3. (2.0 điểm) Trong mặt phẳng Oxy, cho ba điểm A(2; 4), B(-3; 2), C(5; 1).

           a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

           b) Tìm tọa độ điểm K thỏa mãn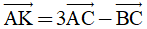

Bài 4. (1.0 điểm) Xác định m để phương trình x(x + 4) + m + 5 = 0 có hai nghiệm cùng dấu.

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 7)

I. TRẮC NGHIỆM (5 ĐIỂM)

Câu 1. Giao điểm của (P): y = x² - 3x - 1 với đường thẳng (d): y = 2 -x là

A. M(1; 1), N(-3; 5)     

B. M(-3; 0)     

C. M(-1; 3), N(3; -1)     

D. M(-1; 0), N(3; 0) 

Câu 2. Tìm m để phương trình (m + 1)x² + 3mx - 2 = 0 có hai nghiệm trái dấu.

A. m > -1     

B. m < -1     

C. m ≥ -1     

D. m < 1 

Câu 3. Tập xác định của hàm số 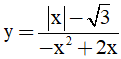 là

A. R\{0; 2}     

B. (0; +∞)\{2}     

C. [3; +∞)     

D. ℝ 

Câu 4. Kết quả của phép toán (-∞; 1] ∩ [-1; 3) là

A. [-1; 1]      

B. (-∞; 3)     

C. (-∞; -1)     

D. (-∞; -1] 

Câu 5. Trong mặt phẳng Oxy cho 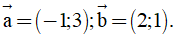Tìm tọa độ của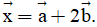  

Câu 6. Mệnh đề nào sau đây là sai?

A. ''∃x ∈ ℝ : x <  ''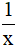      

B. ''∀x ∈ ℝ : x² ≥ x '' 

C. ''∀x ∈ ℝ : x² ≥ 0 ''      

D. ''∃x ∈ ℝ : x² ≤ 0 ''  

Câu 7. Điểm nào sau đây không thuộc đồ thị hàm số y = x² - |x| + 3 ?

A. (3; 9)      

B. (-2; 5)     

C. (-1; 1)     

D. (1; 3) 

Câu 8. Cho hai tập hợp A và B. Khẳng định nào sau đây là đúng?

Câu 9. Bạn An đến siêu thị để mua một chiếc quần Jean và một chiếc áo sơ mi với tổng trị giá là 765.000 đồng (theo giá niêm yết của siêu thị trước đây). Khi đến mua, An được biết hiện hai mặt hàng trên đang được giảm giá. So với giá cũ thì quần được giảm 40%, áo được giảm 30%. Thấy giá rẻ, An đã quyết định mua hai quần và ba áo. Do đó, so với dự tính ban đầu, An đã phải trả thêm 405.000 đồng. Hỏi giá tiền ban đầu của một quần Jean và một áo sơ mi lần lượt là bao nhiêu?

A. 489.000 đồng và 276.000 đồng.    

B. 495.000 đồng và 270.000 đồng.

C. 500.000 đồng và 265.000 đồng.    

D. 485.000 đồng và 280.000 đồng.

Câu 10. Trong mặt phẳng Oxy cho 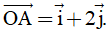 Tọa độ của điểm A là

A. (2; 1)     

B. (0; 2)     

C. (2; 0)     

D. (1; 2)  

Câu 11. Trong mặt phẳng Oxy cho 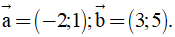 Tính  

Câu 12. Hàm số nào sau đây là hàm số chẵn?

A. y = x³ + 3     

B. y = 3x⁴ - x²     

C. y = |x| + 2x³    

D. y = -2x³ + x 

Câu 13. Điều kiện xác định của phương trình 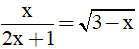 là

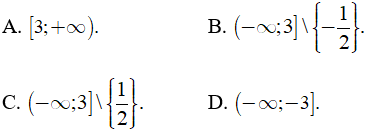
Câu 14. Số nghiệm của phương trình 3x⁴ - 2x² là

A. 1     

B. 2     

C. 4     

D. 3 

Câu 15. Cho ba tập hợp A = (-5; 10], B = (-∞; -2), C = [-2; +∞]. Kết quả của phép toán (A ∩ B) ∪ C là

A. (-5; +∞)     

B. {-2} 

C. ∅     

D. (-5; +∞)\{-2}

Câu 16. Trong mặt phẳng Oxy cho A(1; 2), B(3; -1) và I là trung điểm của đoạn AB. Khẳng định nào sau đây là đúng?

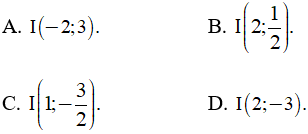
Câu 17. Cho (P): y = ax² + 2x + c có tọa độ đỉnh là I(1; -2). Tìm (P)  

A. (P): y = x² + 2x - 3      

B. (P): y = x² + 2x + 3  

C. (P): y = -x² + 2x - 3      

D. (P): y = -x² + 2x + 3  

Câu 18. Cho hình bình hành ABCD. Khẳng định nào sau đây là sai?

Câu 19. Trong mặt phẳng Oxy cho hai điểm A(-3; 1), B(2; 0) và điểm G(0; 2) là trọng tâm tam giác ABC. Tìm tọa độ điểm C 

A. (0; 6)      

B. (1; 5)      

C. (0; 3)     

D. (-2; 2) 

Câu 20. Nghiệm của phương trình 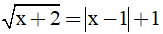 là

A. x = 2; x = -1; x = 0     

B. x = -1 

C. x = 2; x = -1     

D. x = 2 

Câu 21. Parabol y = x² - 3x + 1 có trục đối xứng là đường thẳng có phương trình

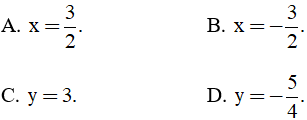
Câu 22. Trong mặt phẳng Oxy cho 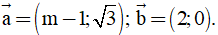Tìm tất cả các giá trị m nguyên dương để góc giữa vectơ 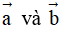bằng 60⁰

A. m = 2     

B. m = 0; m = 2     

C. m = 1     

D. m = 1; m = 3 

Câu 23. Cho mệnh đề P(x): ''∀x ∈ ℝ : x² > 3x - 1''  Mệnh đề phủ định của   là

A.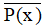: ''∀x ∈ ℝ : x² < 3x - 1''     

B.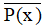 : ''∀x ∈ ℝ : x² ≤ 3x - 1''

C.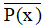 : ''∃x ∈ ℝ : x² < 3x - 1''    

D.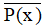 : ''∃x ∈ ℝ : x² ≤ 3x - 1''

Câu 24. Nghiệm của hệ phương trình 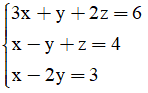 là

A. (x; y; z) = (2; 1; -1)    

B. (x; y; z) = (-1; 1; -2) 

C. (x; y; z) = (1; 1; 2)     

D. (x; y; z) = (1; -1; 2) 

Câu 25. Hàm số nào sau đây nghịch biến trên ℝ 

A. y = 3 - 2x     

B. y = -1 + 3x     

C. y = x - 4    

D. y = √2x - 3 

PHẦN II. TỰ LUẬN ( 5 ĐIỂM)

Câu 1. (1 điểm) Cho tập hợp A = {1,3} và B = {2,3,4}. Tìm tập hợp B\A.

Câu 2. (1 điểm) Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-1;1), B(2,-3) và C(4,5). Tìm tọa độ trung điểm của đoạn thẳng BC và tọa độ trọng tâm G của tam giác ABC.

Câu 3 (1 điểm) Xác định hàm bậc hai y = ax² + bx + c, biết rằng đồ thị hàm số là parabol đi qua điểm A(0;5) và đỉnh I(1;3).

Câu 4. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0;-2), B(5,0) và C(3,5).

a) Chứng minh tam giác ABC vuông cân tại B. Tính diện tích tam giác ABC.

b) Tìm M trên trục Ox sao cho MA² + MB² nhỏ nhất.

Câu 5. (0,5 điểm) Tìm tất cả các giá trị của tham số m để phương trình:

x - x² - 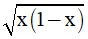 + 3 + 2m = 0 có nghiệm.

Sở Giáo dục và Đào tạo .....

Đề thi Học kì 1

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 8)

I. PHẦN TRẮC NGHIỆM (5 ĐIỂM)

Câu 1: Tam giác ABC vuông ở A và có góc ∠B = 50⁰. Hệ thức nào sau đây là sai?

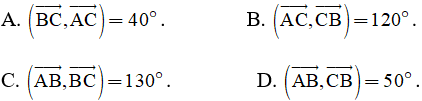
Câu 2: Cho (P): y = -x² - 4x + 3. Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên (-∞; -2).    

B. Hàm số đồng biến trên (-2; +∞).

C. Hàm số đồng biến trên (-∞; -2).    

D. Hàm số nghịch biến trên (-2; +∞).

Câu 3: Nghiệm của phương trình 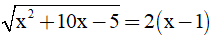 là:

A. x = 3 + √6 và x = 2.    

B. x = 3/4.

C. x = 3 - √6.    

D. x = 3 + √6.

Câu 4: Cho ba tập hợp A = (-5; 10], B = (-∞; -2), C = [-2; +∞). Kết quả của phép toán (A ∩ B) ∪ B là

A. (-5; +∞)         

B. {-2}        

C. ∅             

D. (-5; +∞)\ {-2} 

Câu 5: Parabol y = ax² + bx + c đạt giá trị nhỏ nhất bằng -2 tại x = -2 và đi qua A(0; 6) có phương trình là:

A. y = 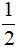x² + 2x + 6.    

B. y = x² + 6x + 6.    

C. y = x² + 2x + 6.    

D. y = x² + x + 4.

Câu 6: Giá trị của m để hàm số y = (2 - m)x + m + 3 nghịch biến là

A. m < 2           B. m > 2           C. m ≥ 2            D. m ≤ 2 

Câu 7: Tập xác định của phương trình: 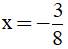 là

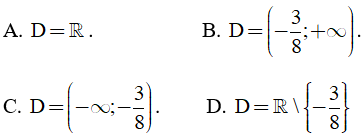
Câu 8: Nghiệm của hệ phương trình 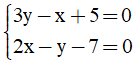 là:

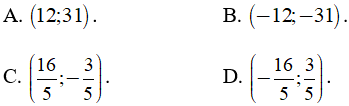
Câu 9: Cặp vectơ nào sau đây vuông góc với nhau?

Câu 10: Trong mặt phẳng tọa độ , cho 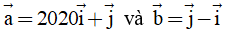. Khi đó, tích vô hướng củ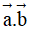a  là

A. -2019.                   B. -2021.                C. 2020.                  D. 2019.

Câu 11: Cho hai tập hợp A = (0; 2020], B = (-2020; 2019). Khi đó A ∩ B là

A. A ∩ B = (-2020; 0].                                  B. A ∩ B = (-2020; 2019].

C. A ∩ B = (-2020; 2020].                            D. A ∩ B = (0; 2019].

Câu 12: Trong mặt phẳng Oxy cho hai véctơ 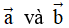biết 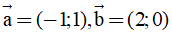. Tính góc giữa hai véctơ .

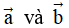A. 45⁰.                         B. 60⁰.                     C. 30⁰.                     D. 135⁰.

Câu 13: Nghiệm của hệ phương trình sau 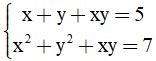 là:

A. (1; 2), (2; 1) .                                               B. (-1; -2), (-2; -1) .

C. (-1; 3), (3; -1).                                             D. (-1; -2) .

Câu 14: Đường thẳng đi qua hai điểm A(-3; 2) và B(-2; 1) có phương trình là

A. y = -x - 1 .              B. y = -x + 1.          C. y = x - 1.            D. y = x + 1.

Câu 15: Tập nghiệm S của phương trình 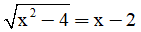 là:

A. S =                   B. S =             C. S =                D. S = ∅

Câu 16: Parabol (P): y = ax² + bx + c đi qua điểm A(-2; -5) và có tọa độ đỉnh I(2; 1) có phương trình là

Câu 17: Cho 2 vectơ 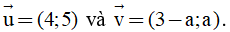Tính a để .

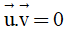A. a = -12.           B. a = 12.           C. a = -3.          D. a = 3.

Câu 18: Tổng lập phương các nghiệm của phương trình 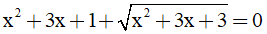 bằng

A. 3                             B. 9                         C. -9                      D. -3

Câu 19: Nghiệm của hệ phương trình 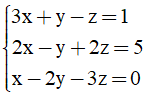 là:

A. (x; y; z) = (2; -1; 1).                                   B. (x; y; z) = (1; -1; -1).

C. (x; y; z) = (1; -1; 1).                                   D. (x; y; z) = (1; 1; -1).

Câu 20: Trong mặt phẳng Oxy, cho hai điểm A(-1; 2), 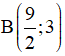 . Tìm tọa độ điểm C trên trục Ox sao cho tam giác ABC vuông tại C và C có tọa độ nguyên.

A. (0; -3).                    B. (-3; 0).                C. (0; 3).                  D. (3; 0).

Câu 21: Khối 10 trường THPT Chuyên có 350 học sinh, trong đó có 200 học sinh đạt học sinh giỏi môn Toán, 150 học sinh đạt học sinh giỏi môn Văn. Biết rằng chỉ có 80 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả hai môn Toán và Văn. Hỏi có bao nhiêu học sinh chỉ học giỏi một môn trong hai môn Toán hoặc Văn?

A. 200 .                        B. 270 .                    C. 80.                       D. 190.

Câu 22: Cho hai điểm A(5;7) và B(3;1). Tính khoảng cách từ gốc O đến trung điểm M của đoạn AB.

A. 5.                            B. √10.                     C. 4√2.                    D. 2√10.

Câu 23: Cho tập A = (-∞; 4], B = (1; 6). Chọn mệnh đề sai.

A. A ∪ B = (-∞; 6]          B. A\B = (-∞; 1]          C. A ∩ B = (1; 4]          D. B\A = (4; 6)

Câu 24: Nghiệm của phương trình 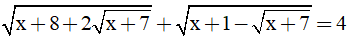 là

A. x = 9.                                                      B. x = -3.

C. x = 2.                                                      D. Phương trình vô nghiệm.

Câu 25: Cho tam giác ABC vuông tại A, có AB = 3, AC = 5 Vẽ đường cao AH. Tích vô hướn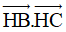g  bằng:

A. √34.              B. 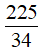. C. -√34. D. -.

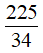II. TỰ LUẬN (7,0 ĐIỂM) 

Câu 1. (2,0 điểm) 

a) Tìm tập xác định, lập bảng biến thiên và vẽ đồ thị hàm số (P): y = x2 – 4x + 2.

b) Dựa vào đồ thị, tìm tham số thực m để -x² + 4x + m² - 5 ≤ 0,∀x ∈ ℝ  

Câu 2. (2,5 điểm)

1. Giải phương trình sau:

a) 2x + 3 = 5 – 6x;

b)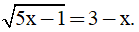  

2. Tìm tham số thực m để phương trình 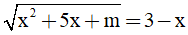 có nghiệm.

Câu 3. (2,5 điểm)

1. Trong mặt phẳng Oxy, cho ba điểm A(3;-2), B(4,-1) và C(2,0).

a) Chứng minh rằng A, B, C là ba đỉnh của tam giác.

b) Tìm tọa độ điểm E sao cho tứ giác ABCE là hình bình hành.

2. Trong mặt phẳng cho hình chữ nhật ABCD. Chứng minh rằng với mọi điểm M bất kì ta luôn có MA² + MC² = MB² + MD².

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---