Giáo án Toán 10 Chương 2: Hàm số bậc nhất và bậc hai (mới, chuẩn nhất)
Với mục đích giúp các Thầy / Cô giảng dạy môn Toán dễ dàng biên soạn Giáo án Toán lớp 10, VietJack biên soạn Bộ Giáo án Toán 10 Chương 2: Hàm số bậc nhất và bậc hai phương pháp mới theo hướng phát triển năng lực bám sát mẫu Giáo án môn Toán chuẩn của Bộ Giáo dục. Hi vọng tài liệu Giáo án Toán 10 này sẽ được Thầy/Cô đón nhận và đóng góp những ý kiến quí báu.
Giáo án Toán 10 Chương 2: Hàm số bậc nhất và bậc hai
Xem thử Giáo án Toán 10 KNTT Xem thử Giáo án Toán 10 CTST Xem thử Giáo án Toán 10 CD
Chỉ từ 300k mua trọn bộ Kế hoạch bài dạy (KHBD) hay Giáo án Toán 10 cả năm (mỗi bộ sách) bản word chuẩn kiến thức, trình bày đẹp mắt:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
- Giáo án Toán 10 Bài 1: Hàm số
- Giáo án Toán 10 Bài 2: Hàm số y = ax + b
- Giáo án Toán 10 Bài 3: Hàm số bậc hai
- Giáo án Toán 10 Ôn tập chương 2 Đại số
Giáo án Toán 10 Bài 1: Hàm số
A. KẾ HOẠCH CHUNG
Tiết 1 |
HOẠT ĐỘNG KHỞI ĐỘNG |
|
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC |
Ôn tập về hàm số |
|
Sự biến thiên của hàm số |
||
Tính chẵn lẻ của hàm số |
||
Tiết 2 |
HOẠT ĐỘNG LUYỆN TẬP HOẠT ĐỘNG VẬN DỤNG HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG |
B. KẾ HOẠCH DẠY HỌC
I. MỤC TIÊU CỦA BÀI:
1. Kiến thức:
- Hiểu khái niệm, tập xác định và đồ thị của hàm số .
- Hiểu các tính chất: hàm số đồng biến, hàm số nghịch biến, hàm số chẵn, hàm số lẻ.
- Biết được tính chất đối xứng của đồ thị hàm số chắn, hàm số lẻ.
2. Kĩ năng:
- Biết tìm tập xác định của các hàm số đơn giản.
- Biết cách chứng minh tính đồng biến, nghịch biến của một hàm số trên một khoảng cho trước.
- Biết xét tính chẵn, lẻ của một hàm số đơn giản.
3. Thái độ:
- Thái độ học tập nghiêm túc, cẩn thận, chính xác,…
4. Định hướng phát triển năng lực:
- Năng lực giao tiếp,
- Năng lực hợp tác, quan sát, phát hiện và giải quyết vấn đề.
- Năng lực tự học, vận dụng các kiến thức đã học vào thực tế cuộc sống,…
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên:
- Giáo án và các dụng cụ dạy học cần thiết: phấn, thước, khăn bảng,…
- Các bảng phụ (máy chiếu) có sẵn: đồ thị các hàm số, các bảng số liệu, biểu đồ,…
- Phiếu học tập
2. Học sinh:
- Các dụng cụ học tập cần thiết: sách giáo khoa, vở ghi, thước, bút,…
- Các bảng phụ, phấn ( hoặc bút lông).
- Ôn tập các kiến thức về hàm số đã học ở cấp THCS.
III. CHUỖI CÁC HOẠT ĐỘNG:
1. Giới thiệu:
*Yêu cầu học sinh trả lời các câu hỏi.
Câu 1: Hình ảnh Cổng Acxơ có gợi cho em nhớ về hình ảnh đồ thị của một hàm số nào mà em đã được học ở THCS?
Câu 2:Ở cấp THCS, các em đã học những loại hàm số nào? Cho ví dụ.
*Đặt vấn đề: Ngoài những loại hàm số mà các em đã học đó, còn có loại hàm số nào khác không? Đồ thị của các hàm số đó sẽ như thế nào?
Hôm nay, chúng ta sẽ tìm hiểu sâu hơn về khái niệm hàm số và vấn đề liên quan đến hàm số.
2. Nội dung bài học:
2.1. ÔN TẬP VỀ HÀM SỐ.
2.1.1. Hàm số. Tập xác định của hàm số.
| HĐ 1: Tiếp cận kiến thức: | Gợi ý | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
- Xét hàm số ----> Ta luôn tính được duy nhất một giá trị của y,∀x∈ℝ ℝ là tập xác định của hàm số - Xét bảng số liệu về tỉ lệ đỗ tốt nghiệp THPT của trường THPT A qua các năm như sau (bảng phụ)
Hãy chỉ ra về tỉ lệ đỗ tốt nghiệp THPT của trường THPT A các năm 2014, 2016, 2017,2013… ---> + Bảng số liệu này cũng là một hàm số. + Tập D = {2014, 2015, 2016, 2017} gọi là tập xác định của hàm số. |
- Có thể sử dụng MTCT hoặc tính nhẩm. + Ứng với mỗi giá trị của x ta chỉ tính ra duy nhất một giá trị của y. + Có giá trị nào của x mà ta không tính được y? - Hs quan sát bảng số liệu và đọc kết quả. + Ứng với mỗi năm 2014, 2016, 2017,… chỉ có một tỉ lệ đỗ (một kết quả) xác định. + Dựa vào bảng số liệu này ta chỉ biết được tỉ lệ đỗ tốt nghiệp THPT của trường THPT A các năm 2014, 2015, 2016, 2017; không thể xác định tỉ lệ đỗ tố nghiệp THPT năm 2013 của trường THPT A nếu dựa vào bẳng số liệu này. |
| HĐ 2: Hình thành kiến thức: | Gợi ý |
|---|---|
- Yêu cầu học sinh: Từ các ví dụ trên + tham khảo sách giáo khoa để đưa ra định nghĩa về hàm số, tập xác định của hàm số. + Nếu với mỗi giá trị của x thuộc tập D có một và chỉ một giá trị tương ứng của y thuộc tập số thực ℝ thì ta có một hàm số. Ta gọi x là biến số và y là hàm số của x. Tập hợp D được gọi là tập xác định của hàm số |
- Học sinh thảo luận+ tham khảo sgk để đưa ra định nghĩa hàm số, tập xác định của hàm số. - Đặc biệt nhấn mạnh mối quan hệ tương ứng 1-1 giữa biến số và hàm số của biến. |
| HĐ 3: Củng cố: | Gợi ý |
|---|---|
1. Yêu cầu học sinh:+ Cho hàm số dạng Tính y tại x=0,x=2,x=-4,x=-1,x=1 + Chỉ ra tập xác định của hàm số đó. 2. Yêu cầu học sinh: + Cho một hàm số dạng bảng số liệu (tương tự bảng số liệu về tỉ lệ đỗ tốt nghiệp THPT của trường THPT A qua các năm) + Chỉ một vài cặp giá trị của biến số và hàm số của biến. + Chỉ ra tập xác định của hàm số đó. |
1. Các nhóm hoạt động độc lập và trình bày kết quả lên bảng phụ. + Gv chia lớp làm 8 nhóm: 4 nhóm thực hiện yêu cầu 1, 4 nhóm thực hiện yêu cầu 2. + Các nhóm ghi kết quả lên bảng phụ và cử đại diện lên báo cáo trước lớp, các nhóm khác theo dõi và góp ý nếu cần (chỉ cần 2 nhóm báo cáo, các nhóm khác gv trực tiếp theo dõi và hướng dẫn hoàn thiện sản phẩm trong quá trình các em thực hiện yêu cầu). |
2.1.2. Cách cho hàm số
| HĐ 1: Tiếp cận kiến thức: | Gợi ý |
|---|---|
- Từ các ví dụ ở phần trên, yêu cầu học sinh chỉ ra một vài cách cho hàm số. - Liệu còn cách cho hàm số nào khác không? |
+ Hàm số + Bảng số liệu về tỉ lệ đỗ tốt nghiệp THPT của trường THPT A qua các năm là một hàm số cho dưới dạng bảng số liệu. |
| HĐ 2: Hình thành kiến thức: | Gợi ý |
|---|---|
*Ta có 3 cách cho hàm số : + Hàm số cho bằng công thức. + Hàm số cho bằng bảng. + Hàm số cho bằng biểu đồ. |
- Từ các ví dụ ở phần trên, học sinh chỉ ra được 2 cách cho hàm số: bằng công thức. Và bằng bảng số liệu. - Khi học môn Địa lí, các bảng số liệu còn được mô tả ở dạng nào? ---> Hàm số còn có thể được cho ở dạng biểu đồ |
|
* Cách tìm Tập xác định của hàm số: + Đối với các hàm số cho bằng bảng hoặc cho bằng biểu đồ, ta có thể quan sat và xác định ngay tập xác định của nó. |
+ Nhắc lại Tập xác định của hàm số: Bảng số liệu về tỉ lệ đỗ tốt nghiệp THPT của trường THPT A qua các năm. + Gv cho một hàm số dạng đồ thị và yêu cầu học sinh chỉ ra tập xác định của nó.( sử dụng bảng phụ có sẵn đồ thị ( Hình 13_sgk/trang 33 hoặc tương tự) |
|
+ Đối với hàm số cho dưới dạng công thức: Quy ước: Tập xác định của hàm số f(x) là tập hợp tất cả các giá trị của x sao cho biểu thức f(x) có nghĩa. Ví dụ: Tìm tập xác định của các hàm số (Học sinh thực hiện ví dụ theo hướng dẫn của gv). |
+ Cho hàm số + Các biểu thức đại số có nghĩa khi nào? |
|
* Chú ý: Hàm số có thể được xác định bởi hai, ba,..công thức. Ví dụ:Hàm số Tập xác định của hàm số này là: |
+Với x > thì hàm số xác định bởi bởi biểu thức nào? +Với x≤2 thì hàm số xác định bởi bởi biểu thức nào? +Với 2 <x≤3 thì hàm số xác định bởi bởi biểu thức nào? -----> Tập xác định của hàm số này là gì? |
| HĐ 3: Củng cố: | Gợi ý |
|---|---|
1. Tìm tập xác định của các hàm số 2. Tìm tập xác định của các hàm số |
1. Các nhóm hoạt động độc lập và trình bày kết quả lên bảng phụ. + Gv chia lớp làm 8 nhóm: 4 nhóm thực hiện yêu cầu 1, 4 nhóm thực hiện yêu cầu 2. + Các nhóm ghi kết quả lên bảng phụ và cử đại diện lên báo cáo trước lớp, các nhóm khác theo dõi và góp ý nếu cần để hoàn thiện sản phẩm. + Giáo viên theo dõi qua trình làm việc của học sinh và đưa ra nhận xét chung. |
2.1.3. Đồ thị của hàm số:
| HĐ 1: Tiếp cận kiến thức: | Gợi ý |
|---|---|
- Yêu cầu học sinh vẽ đồ thị hàm số y=2x-1 lên bảng phụ. |
* Gv theo dõi quá trình làm việc của các nhóm, chọn ra nhóm có sản phẩm đúng nhất, yêu cầu đại diện nhóm đó trình bày cách thực hiện. ----> đồ thị hàm số là đường gì? |
- Gv trình chiếu (hoặc dùng bảng phụ) đồ thị hàm số ---> Đồ thị của các hàm số khác là đường gì? Vậy đồ thị hàm số là gì? |
+ Học sinh quan sát và nhớ lại kiến thức. -----> Đồ thị hàm số là đường gì? |
| HĐ 2: Hình thành kiến thức: | Gợi ý |
|---|---|
1. Đồ thị hàm số y=f(x) xác định trên tập D là tập hợp tất cả các điểm M(x,f(x)) trên mặt phẳng tọa độ với mọi x thuộc D. |
|
- Gv có thể trình chiêu đồ thị của một số hàm số khác để học sinh tham khảo. |
| HĐ 3: Củng cố: | Gợi ý |
|---|---|
|
1. Dựa vào đồ thị hàm số Y=f(x)=2x-1 ( có hình vẽ minh họa) a) Tính f(-2),f(0),f(5),f(10) . b) Tìm x sao cho f(x)=3 (bằng hình vẽ và bằng phép tính). 2. Dựa vào đồ thị hàm số y=f(x)=x2 ( có hình vẽ minh họa) a) Tính f(-2),f(0),f(10) . b) Tìm x sao cho f(x)=4 (bằng hình vẽ và bằng phép tính). |
|
- Các nhóm học sinh hoạt động độc lập và trình bày kết quả lên bảng phụ. + Gv chia lớp làm 8 nhóm: 4 nhóm thực hiện yêu cầu 1, 4 nhóm thực hiện yêu cầu 2. + Các nhóm ghi kết quả lên bảng phụ và cử đại diện lên báo cáo trước lớp, các nhóm khác theo dõi và góp ý nếu cần để hoàn thiện sản phẩm. + Giáo viên theo dõi, hướng dẫn quá trình làm việc của các nhóm học sinh và đưa ra nhận xét chung. |
2.2. SỰ BIẾN THIÊN CỦA HÀM SỐ.
| HĐ 1: Tiếp cận kiến thức: | Gợi ý |
|---|---|
|
- Xét đồ thị hàm số + Hàm số + Hàm số ----> Hàm số như thế nào được gọi là hàm số đồng biến trên khoảng (a,b) ? hàm số nghịch biến trên khoảng (a,b) ? |
|
*Học sinh quan sát hình vẽ và trả lời câu hỏi: - Trên khoảng (0;+∞) , + Theo hướng từ trái sang phải, đồ thị hàm số đi lên hay đi xuống? + Với x1 ,x2 ∈ (0;+∞), x1 < x2 so sánh f(x1) và f(x2) . - Trên khoảng (-∞;0) , + Theo hướng từ trái sang phải, đồ thị hàm số đi lên hay đi xuống? + Với x1 ,x2 ∈ (-∞;0), x1 < x2 , so sánh f(x1) và f(x2) . |
| HĐ 2: Hình thành kiến thức: | Gợi ý |
|---|---|
|
- Yêu cầu học sinh: Từ các ví dụ trên + tham khảo sách giáo khoa để đưa ra khái niệm hàm số đồng biến trên khoảng (a,b) ? hàm số nghịch biến trên khoảng (a,b) ? + Để chứng minh hàm số y=f(x) đồng biến trên khoảng (a,b) ta chứng minh x1,x2∈(a,b) ,x1 < x2 thì f(x1) < f(x2) . ( hoặc chứng minh x1,x2∈(a,b), + Để chứng minh hàm số y=f(x) nghịch biến trên khoảng (a,b) ta chứng minh x1,x2∈(a,b) ,x1 < x2 thì f(x1) > f(x2) . ( hoặc chứng minh x1,x2∈(a,b), - Chú ý: sgk/trang 36 - Nhắc lại tính đồng biến, nghịch biến của các hàm số y=ax+b , y=ax2 (đã học ở THCS). - Gv thuyết giảng: + Xét chiều biến thiên của hàm số là tìm các khoảng đồng biến và nghịch biến của nó. + Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên của hàm số đó (giáo viên có thể minh họa bằng hình vẽ bảng biến thiên của hàm số |
|
- Học sinh thảo luận, tham khảo sgk để đưa ra: + Khái niệm hàm số đồng biến trên khoảng (a,b) ? hàm số nghịch biến trên khoảng (a,b) ? + Cách chứng minh hàm số đồng biến trên khoảng (a,b) ? hàm số nghịch biến trên khoảng (a,b) ? + Nhận xét về dấu của 2 biểu thức x1-x2 và f(x1)-f(x2) - trong các trường hợp hàm số đồng biến trên khoảng (a,b) , hàm số nghịch biến trên khoảng (a,b) với x1,x2∈(a,b) + Nếu a > 0 , hàm số y=ax+b đồng biến trên R . Nếu a <0 , hàm số y=ax+b nghịch biến trên R . + Nếu a > 0 , hàm số y=ax2 đồng biến trên (0;+∞) nghịch biến trên khoảng (-∞;0) . Nếu a <0 , hàm số y=ax2 đồng biến trên (-∞;0) nghịch biến trên khoảng (0;+∞) . - Học sinh lắng nghe và nắm kiến thức. + Để diễn tả hàm số đồng biến trên khoảng (a,b) ta vẽ dấu mũi tên đi lên (từ a đến b). + Để diễn tả hàm số nghịch biến trên khoảng (a,b) ta vẽ dấu mũi tên đi lên (từ a đến b). + Bảng biến thiên của hàm số có thể giúp ta sơ bộ hình dung được đồ thị của hàm số đó (đi lên trong khoảng nào, đi xuống trong khoảng nào). |
| HĐ 3: Củng cố: | Gợi ý |
|---|---|
|
PHIẾU HỌC TẬP 1. Cho bảng biến thiên của hàm số y=-2x2 (có hình vẽ kèm theo). Em hãy chỉ ra các khoảng đồng biến và các khoảng nghịc biến của hàm số y=-2x2 . 2. Cho đồ thị hàm số y=x3+3x2-2 (có hình vẽ kèm theo). Em hãy lập bảng biến thiên của hàm số y=x3+3x2-2 . 3. Chứng minh hàm số y=-2x+1 nghịch biến trên R . |
|
- Giáo viên phát phiếu học tập cho các nhóm, đồng thời treo bảng phụ (hoặc trình chiếu) nội dung lên bảng. - Các nhóm hoạt động độc lập và trình bày kết quả lên bảng phụ. - Giáo viên theo dõi, hướng dẫncác nhóm thực hiên, sau đó chọn nhóm có kết quả đúng nhất và đề nghị nhóm cử đại diện lên báo cáo trước lớp, các nhóm khác theo dõi và góp ý nếu cần. |
2.3. TÍNH CHẴN LẺ CỦA HÀM SỐ.
| HĐ 1: Tiếp cận kiến thức: | Gợi ý |
|---|---|
|
- Xét hàm số y=f(x)=3x ,(có minh họa bằng đồ thị trên bảng phụ hoặc trình chiếu). ---> y=f(x)=3x là một hàm số lẻ. - Xét hàm số y=f(x)=-3x2 ,(có minh họa bằng đồ thị trên bảng phụ hoặc trình chiếu). --->y=f(x)=-3x2 là một hàm số chẵn. |
|
- Thực hiện các phép toán so sánh đồng thời quan sát đồ thị. + so sánh f(-1) và f(1) , f(-2) và f(2) ,f(5) và f(-5) ,f(10) và f(-10) ,f(-25) và f(25) . + So sánh f(x) và f(-x) ? - Thực hiện các phép toán so sánh đồng thời quan sát đồ thị. + so sánh f(-1) và f(1) , f(-2) và f(2) ,f(5) và f(-5), f(10) và f(-10) , f(-25) và f(25) + So sánh f(x) và f(-x) ? |
| HĐ 2: Hình thành kiến thức: | Gợi ý |
|---|---|
|
- Hàm số y=f(x) với tập xác định D gọi là hàm số chẵn nếu: ∀x∈D thì -x∈D và f(-x)=f(x) - Hàm số y=f(x) với tập xác định D gọi là hàm số lẻ nếu: ∀x∈D thì -x∈D và f(-x)=-f(x) - Hàm số y=f(x) với tập xác định D có thể không phải là hàm số chẵn, cũng không phải hàm số lẻ. ( nếu: ∃x∈D mà -x∉D Hoặc ∀x∈D thì -x∈D mà f(-x)≠f(x) và f(-x)≠-f(x) - Các bước xét tính chẵn, lẻ của hàm số: + Tìm tập xác định D của hàm số. + Kiểm tra tính đối xứng của D ( ∀x∈D thì -x∈D ?) ---> nếu: ∃x∈D mà -x∉D thì y=f(x) không phải là hàm số chẵn, cũng không phải hàm số lẻ. + Tính f(-x) ,so sánh với f(x) rồi kết luận. - Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng. - Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng. |
|
- Từ kết quả so sánh f(x) và f(-x) ở các ví dụ phần trên, học sinh chỉ ra được: + Hàm số y=f(x) là hàm số chẵn nếu f(x) và f(-x) như thế nào với nhau? + Hàm số y=f(x) là hàm số lẻ nếu f(x) và f(-x) như thế nào với nhau? + Nếu f(x) xác định và f(-x) không xác định (hoặc f(x) không xác định và f(-x) xác định) thì sao? ---> Nhận xét gì về tập xác định của hàm số chẵn, hàm số lẻ? + Nếu hàm số y=f(x) với tập xác định D có ∀x∈D thì -x∈D mà f(-x)≠f(x) và f(-x)≠-f(x) thì sao? -----> Các bước xét tính chẵn, lẻ của hàm số? - Cho y=f(x)=-3x2 là một hàm số chẵn. Nhận xét về vị trí các điểm có tọa độ (x,f(x)) và (-x,f(-x)) trên hệ trục Oxy? ---> Tính đối xứng của đồ thị hàm số chẵn? - Cho y=f(x)=3x là một hàm số lẻ. Nhận xét về vị trí các điểm có tọa độ (x,f(x)) và (-x,f(-x)) trên hệ trục Oxy? ---> Tính đối xứng của đồ thị hàm số lẻ? |
| HĐ 3: Củng cố: | Gợi ý |
|---|---|
|
1. Xét tính chẵn, lẻ của các hàm số sau? 2. Xét tính chẵn, lẻ của các hàm số |
|
- Gv chia lớp làm 8 nhóm: 4 nhóm thực hiện yêu cầu 1, 4 nhóm thực hiện yêu cầu 2. - Các nhóm hoạt động độc lập và trình bày kết quả lên bảng phụ. - Gv chọn 2 nhóm cử đại diện lên báo cáo trước lớp( 1 nhóm thực hiện yêu cầu 1, 1 nhóm thực hiện yêu cầu 2), các nhóm khác theo dõi và góp ý nếu cần để hoàn thiện sản phẩm. + Giáo viên theo dõi qua trình làm việc của học sinh và đưa ra nhận xét chung. |
.....................................................................................................
.....................................................................................................
.....................................................................................................
.....................................................................................................
Giáo án Toán 10 Bài 2: Hàm số y = ax + b
A. KẾ HOẠCH CHUNG
Tiết 1 |
HOẠT ĐỘNG KHỞI ĐỘNG |
|
HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC |
Ôn tập hàm số bậc nhất |
|
Hàm số hằng y = b |
||
Hàm số y = |x| |
||
Tiết 2 |
HOẠT ĐỘNG LUYỆN TẬP HOẠT ĐỘNG VẬN DỤNG HOẠT ĐỘNG TÌM TÒI, MỞ RỘNG |
B. KẾ HOẠCH DẠY HỌC
I. MỤC TIÊU CỦA BÀI:
1. Kiến thức:
- Hiểu được sự biến thiên và đồ thị của hàm số bậc nhất. Hiểu cách vẽ đồ thị hàm số bậc nhất và đồ thị hàm số y = |x|.Biết đồ thị hàm số này nhận Oy làm trục đối xứng.
-Học sinh vẽ thành thao đồ thị các hàm số đã học và xác định chiều biến thiên của nó. Biết cách phân tích để vẽ được đồ thị của hàm số cho bởi nhiều công thức.
2. Kĩ năng
-Biết cách chứng minh một hàm số nghịch biến,đồng biến trên một khoảng xác định
-Biết cách chứng minh một hàm số chẳn hoặc lẻ
- Thành thạo việc xét chiều biến thiên và vẽ đồ thị hàm số bậc nhất. Vẽ được đồ thị hàm số y = b ; y = |x|
-Biết tìm toạ độ giao điểm của hai đường thẳng có phương trình cho trước. Tìm phương trình đường thẳng khi biết hai điểm mà nó đi qua
3.Thái độ
-Giáo dục cho học sinh tính cần cù,chịu khó trong suy nghĩ
- Giáo dục cho học sinh tính cẩn thận ,chính xác,yêu thích môn học
4. Năng lực cần phát triển
+ Năng lực tự học: Học sinh xác định đúng đắn động cơ thái độ học tập; tự đánh giá và điều chỉnh được kế hoạch học tập; tự nhận ra sai sót và cách khắc phục sai sót.
+ Năng lực giải quyết vấn đề: Biết tiếp nhận câu hỏi, bài tập hoặc đặt ra câu hỏi. Phân tích được các tình huống trong học tập
+ Năng lực tự quản lý: Làm chủ cảm xúc của bản thân trong quá trình học tập và trong cuộc sống; trưởng nhóm biết quản lý nhóm mình, phân cụ thể cho từng thành viên của nhóm, các thành viên tự ý thức được nhiệm vụ của mình và hoàn thành được nhjiệm vụ được giao.
+ Năng lực giao tiếp: Tiếp thu kiến thức, trao đổi học hỏi bạn bè thông qua hoạt động nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.
+ Năng lực hợp tác: xác định được nhiệm vụ của nhóm, trách nhiệm của bản thân, đưa ra ý kiến đóng góp hoàn thành nhiệm vụ của chuyên đề.
+ Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ toán học.
+ Năng lực sử dụng công nghệ thông tin và truyền thông
+ Năng lực tự học
+ Năng lực giải quyết vấn đề
+ Năng lực tính toán
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
1. Giáo viên:
- Giáo án và các dụng cụ dạy học cần thiết: phấn, thước, khăn bảng,…
- Phiếu học tập, giao nhiệm vụ về nhà cho HS nghiên cứu trước chủ đề…
2. Học sinh:
- Các dụng cụ học tập cần thiết: sách giáo khoa, vở ghi, thước, bút,…
- Các bảng phụ, phấn (hoặc bút lông).
- Ôn tập các kiến thức về hàm số đã học ở cấp THCS, chuẩn bị trước các nội dung giáo viên giao.
III. CHUỖI CÁC HOẠT ĐỘNG:
1. Giới thiệu:
Bài toán máy bơm:
Một hộ gia đình có ý định mua một cái máy bơm để phục vụ cho việc tưới tiêu vào mùa hạ. Khi đến
cửa hàng thì được ông chủ giới thiệu về hai loại máy bơm có lưu lượng nước trong một giờ và chất lượng máy là như nhau.
Máy thứ nhất giá 1500000đ và trong một giờ tiêu thụ hết 1,2kW.
Máy thứ hai giá 2000.000đ và trong một giờ tiêu thụ hết 1kW
Theo bạn người nông dân nên chọn mua loại máy nào để đạt hiệu quả kinh tế cao ?
2. Nội dung bài học:
2.1. ÔN TẬP VỀ HÀM SỐ BẬC NHẤT
2.2. HÀM SỐ HẰNG y = b.
- Yêu cầu các nhóm trình bày bảng phụ ghi nội dung 2 phần trên đã được giao trước.
- Giáo viên chốt lại kiến thức.
2.2. HÀM SỐ y = |x| .
a. Tiếp cận:
- Chỉ ra tập xác định của hàm số y = |x| và cho biết hàm số đã cho đồng biến, nghịch biến trên khoảng nào? Vì sao?
- Dựa vào chiều biến thiên của đồ thị hàm số hãy vẽ bảng biến thiên?
b. Hình thành kiến thức:
- Tập xác định: D=R
- Hàm số y = |x| nghịch biến trên khoảng (-∞;0) và đồng biến trên khoảng (0;+∞).
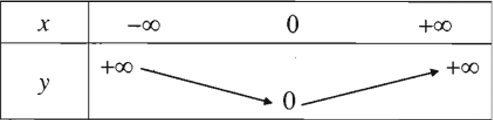
*Bảng biến thiên:
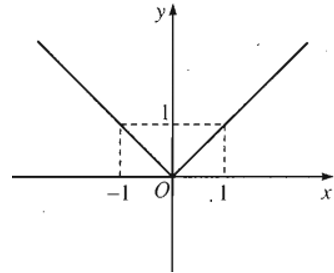
*Đồ thị:
- Hàm số y =|x| là một hàm số chẵn, nhận trục Oy làm trục đối xứng.
c. Củng cố:
Ví dụ: Vẽ đồ thị hàm số y =|x-1| .
- GV hướng dẫn học sinh cách vẽ đồ thị hàm số y =|ax+b| .
.....................................................................................................
.....................................................................................................
.....................................................................................................
.....................................................................................................
Xem thử Giáo án Toán 10 KNTT Xem thử Giáo án Toán 10 CTST Xem thử Giáo án Toán 10 CD
Xem thêm các bài soạn Giáo án Toán lớp 10 theo hướng phát triển năng lực mới nhất, hay khác:
- Giáo án Toán 10 Chương 1: Mệnh đề - Tập hợp
- Giáo án Toán 10 Chương 3: Phương trình. Hệ phương trình
- Giáo án Toán 10 Chương 4: Bất đẳng thức. Bất phương trình
- Giáo án Toán 10 Chương 5: Thống kê
- Giáo án Toán 10 Chương 6: Cung và góc lượng giác. Công thức lượng giác
- Giáo án Toán 10 Chương 1: Vectơ
- Giáo án Toán 10 Chương 2: Tích vô hướng của hai vectơ và ứng dụng
- Giáo án Toán 10 Chương 3: Phương pháp tọa độ trong mặt phẳng
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giáo án Toán 10 cả ba sách mới của chúng tôi được biên soạn bám sát chuẩn Giáo án môn Toán 10 của Bộ GD & ĐT.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 10 (các môn học)
- Giáo án điện tử lớp 10 (các môn học)
- Giáo án Ngữ văn 10
- Giáo án Toán 10
- Giáo án Tiếng Anh 10
- Giáo án Vật Lí 10
- Giáo án Hóa học 10
- Giáo án Sinh học 10
- Giáo án Lịch Sử 10
- Giáo án Địa Lí 10
- Giáo án Kinh tế Pháp luật 10
- Giáo án Tin học 10
- Giáo án Công nghệ 10
- Giáo án Giáo dục quốc phòng 10
- Giáo án Hoạt động trải nghiệm 10
- Đề thi lớp 10 (các môn học)
- Đề thi Ngữ Văn 10 (có đáp án)
- Chuyên đề Tiếng Việt lớp 10
- Đề cương ôn tập Văn 10
- Đề thi Toán 10 (có đáp án)
- Đề thi cương ôn tập Toán 10
- Đề thi Toán 10 cấu trúc mới (có đáp án)
- Đề thi Tiếng Anh 10 (có đáp án)
- Đề thi Vật Lí 10 (có đáp án)
- Đề thi Hóa học 10 (có đáp án)
- Đề thi Sinh học 10 (có đáp án)
- Đề thi Lịch Sử 10 (có đáp án)
- Đề thi Địa Lí 10 (có đáp án)
- Đề thi Kinh tế & Pháp luật 10 (có đáp án)
- Đề thi Tin học 10 (có đáp án)
- Đề thi Công nghệ 10 (có đáp án)
- Đề thi Giáo dục quốc phòng 10 (có đáp án)


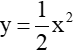 . Hãy tính các giá trị của y khi x=1,x=0,x=-2,x=5,x=-4...
. Hãy tính các giá trị của y khi x=1,x=0,x=-2,x=5,x=-4...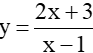
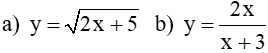
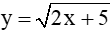 . Ta có thể quan sát và nhận thấy tập xác định của hàm số này không?
. Ta có thể quan sát và nhận thấy tập xác định của hàm số này không?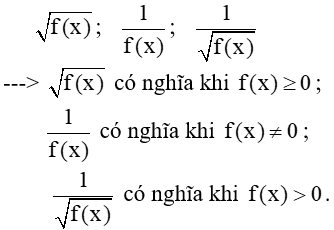
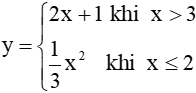
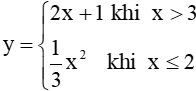
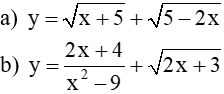
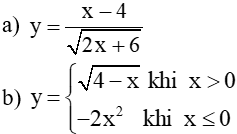
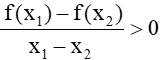 )
)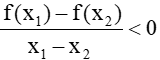 )
)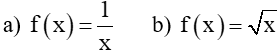
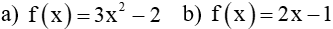



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

