Đáp án Đề minh họa năm 2019 môn Toán (có giải chi tiết)
Đáp án Đề minh họa năm 2019 môn Toán
Xem thử Đề thi Tốt nghiệp Toán 2025 Xem thử Đề thi Tốt nghiệp Văn 2025 Xem thử Đề thi Tốt nghiệp Anh 2025 Xem thử Đề thi Tốt nghiệp Vật Lí 2025 Xem thử Đề thi Tốt nghiệp Hóa 2025 Xem thử Đề thi Tốt nghiệp Sinh 2025 Xem thử Đề thi Tốt nghiệp Sử 2025 Xem thử Đề thi Tốt nghiệp Địa 2025 Xem thử Đề thi Tốt nghiệp KTPL 2025
Chỉ từ 300k mua trọn bộ đề thi Tốt nghiệp THPT năm 2025 các môn học theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
Xem: Đề minh họa năm 2019 môn Toán
Đáp án:
| 1 - A | 2 - D | 3 - A | 4 - D | 5 - B | 6 - C |
| 7 - A | 8 - B | 9 - C | 10 - B | 11 - C | 12 - A |
| 13 - B | 14 - D | 15 - B | 16 - D | 17 - A | 18 - D |
| 19 - B | 20 - B | 21 - A | 22 - B | 23 - C | 24 - D |
| 25 - A | 26 - C | 27 - A | 28 - D | 29 - A | 30 - D |
| 31 - A | 32 - C | 33 - D | 34 - A | 35 - C | 36 - C |
| 37 - D | 38 - B | 39 - C | 40 - A | 41 - A | 42 - B |
| 43 - D | 44 - A | 45 - C | 46 - A | 47 - D | 48 - C |
| 49 - C | 50 - B |
Hướng dẫn giải chi tiết:
Câu 1:
Thể tích khối lập phương cạnh 2a là: V = (2a)3 = 8a3.
Câu 2:
Nhìn vào bảng biến thiên ta thấy hàm số đạt giá trị cực đại tại x = 2 và giá trị cực đại bằng 5.
Câu 3:
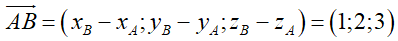
Câu 4:
Hàm số đồng biến ⇔ đồ thị hàm số đi lên
Quan sát đồ thị thấy hàm số đồng biến trên (–1; 0) và (1; +∞)
Câu 5:
Áp dụng công thức loga(b1b2) = logab1 + logab2 và logabα = α.logab ta có: log(ab2) = log a + log b2 = log a + 2.log bCâu 6:
Ta có:
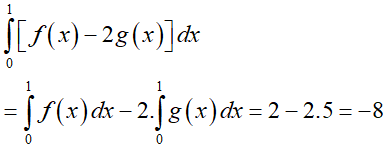
Câu 7:
Theo công thức, thể tích khối cầu bán kính a bằng:
Câu 8:
Tập xác định: D = R.
log2(x2 - x + 2) = 1
⇔ x2 – x + 2 = 2
⇔ x2 – x = 0
⇔ x(x – 1) = 0
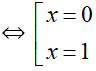
Vậy tập nghiệm của phương trình là {0 ; 1}
Câu 9:
Mặt phẳng (Oxz) có phương trình y = 0.
Câu 10:
Ta có :
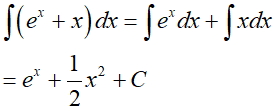
Câu 11:
Thay lần lượt tọa độ các điểm vào phương trình đường thẳng d ta thấy chỉ có điểm P(1; 2; 3) thỏa mãn:
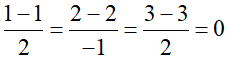
Câu 12:
Ta có công thức
Câu 13:
Ta có: un = u1 + (n – 1).d
Do đó: u4 = u1 + 3d = 2 + 3.5 = 17.
Câu 14:
Điểm biểu diễn số phức z = ai + b có tọa độ (a ; b)
Điểm biểu diễn số phức z = –1 + 2i có tọa độ (–1 ; 2) và là điểm Q.
Câu 15:
Từ hình dạng đồ thị ta thấy đây là đồ thị hàm số dạng
Đồ thị có đường tiệm cận đứng
Đồ thị có đường tiệm cận ngang
Chỉ có đồ thị hàm số 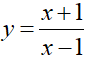
Câu 16:
Quan sát đồ thị ta thấy trên [–1 ; 3]
+ Hàm số đạt giá trị lớn nhất tại x = 3, giá trị lớn nhất M = 3.
+ Hàm số đạt giá trị nhỏ nhất tại x = 2, giá trị nhỏ nhất m = –2.
Vậy M – m = 5.
Câu 17:
Xét : f’(x) = 0
⇔ x(x – 1)(x + 2)3 = 0
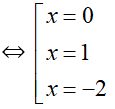
Ta có bảng biến thiên:
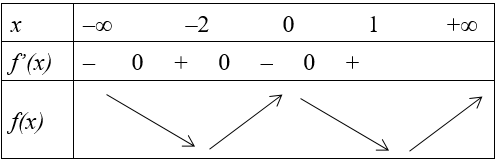
Dựa vào bảng biến thiên thấy hàm số có ba điểm cực trị
Câu 18:
Ta có: 2a + (b + i).i = 1 + 2i
⇔ 2a + bi + i2 = 1 + 2i
⇔ 2a – 1 + bi = 1 + 2i (Vì i2 = –1)
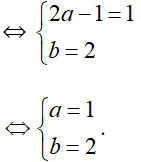
Câu 19:
Bán kính mặt cầu:
Phương trình mặt cầu tâm I(1; 1; 1) và bán kính R = √5 là:
(x – 1)2 + (y – 1)2 + (z – 1)2 = 5.
Câu 20:
Ta có:
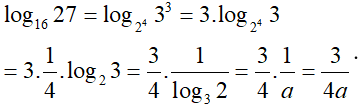
Câu 21:
Giải phương trình z2 – 3z + 5 = 0 ta có hai nghiệm:
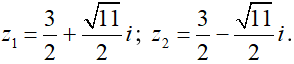
Do đó:
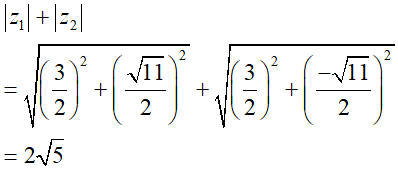
Câu 22:
Ta có: (P) nhận n→ = (1; 2; 2) là một vtpt
(Q) cũng nhận n→ = (1; 2; 2) là một vtpt
⇒ (P) // (Q)
⇒ d((P); (Q)) = d(M; (Q)) với M là một điểm bất kì thuộc mặt phẳng (P).
Chọn M(0 ; 0 ; 5).
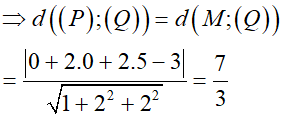
Câu 23:
Tập xác định: D = R.
3x2 - 2x < 27
⇔ x2 – 2x < 3
⇔ x2 – 2x – 3 < 0
⇔ (x + 1)(x – 3) < 0
⇔ –1 < x < 3 .
Vậy tập nghiệm của bất phương trình là (–1; 3).
Câu 24:
Phần hình phẳng gạch chéo trong hình vẽ là phần hình giới hạn bởi đồ thị hàm số y = x2 – 2x – 1 , đồ thị hàm số y = –x2 + 3 và các đường thẳng x = –1, x = 2.
Vậy diện tích phần hình đó là:
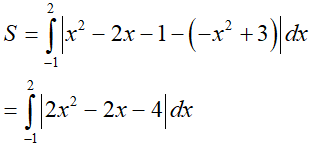
Mà trong (–1; 2), 2x2 – 2x – 4 < 0 nên |2x2 – 2x – 4| = –2x2 + 2x + 4.
Do đó :
Câu 25:
+ Đáy của khối nón là hình tròn có bán kính R = a.
⇒ Diện tích mặt đáy của khối nón là: S = π.a2.
+ Gọi chiều cao của khối nón là h
Ta có: đường sinh bằng 2a ⇒ l = 2a
Mà: l2 = h2 + R2 ⇒ h2 = l2 - R2 = 3a2 ⇒ h = a√3 .
Vậy thể tích khối nón là
Câu 26:
Ta có : 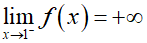
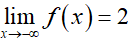
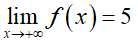
Vậy hàm số tổng ba tiệm cận đứng và ngang.
Câu 27:
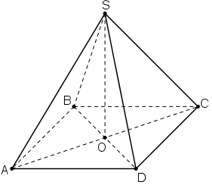
S.ABCD là khối chóp tứ giác đều nên SO ⊥ (ABCD) nên 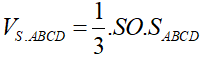
+ SABCD = 4a2.
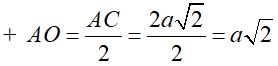
ΔSOA vuông tại O 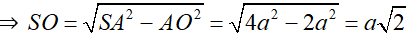
Vậy thể tích khối chóp bằng 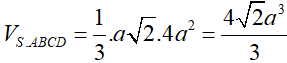
Câu 28:
Ta có :
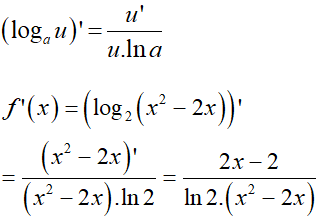
Câu 29:
2.f(x) + 3 = 0
Số nghiệm thực của phương trình 2.f(x) + 3 = 0 là số nghiệm thực của phương trình 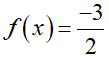
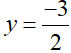
Dựa vào bảng biến thiên ta thấy đường thẳng 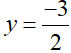
Vậy phương trình có bốn nghiệm
Câu 30:
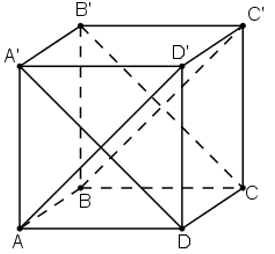
Để tính góc giữa hai mặt phẳng, ta góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Ta có : ABCD.A’B’C’D’ là hình lập phương
⇒ A’B’ ⊥ (AA’D’D)
⇒ A’B’ ⊥ AD’.
Mà: A’D ⊥ AD’
A’B’ cắt A’D
⇒ (A’B’CD) ⊥ AD’ (1)
Chứng minh tương tự ta có: (ABC’D’) ⊥ A’D (2)
⇒ ((A’B’CD) ; (ABC’D’)) = (AD’; A’D).
Mà AA’D’D là hình vuông nên AD’ ⊥ AD’ ⇒ (AD’; A’D) = 900
⇒ ((A’B’CD) ; (ABC’D’)) = 900.
Câu 31:
Xét phương trình : log3(7 - 33) = 2 - x (1)
Điều kiện xác định: 7 – 3x > 0
(1) ⇔ 7 – 3x = 32-x
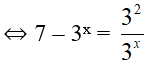
⇔ 7.3x – (3x)2 = 32
⇔ 32x – 7.3x + 9 = 0
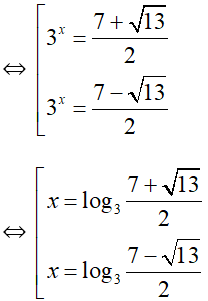
Tổng các nghiệm của phương trình là:
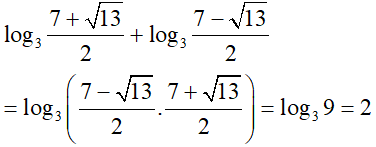
Câu 32:
Thể tích khối trụ bằng: V = πr2h, trong đó r là bán kính đáy khối trụ, h là chiều cao khối trụ.
Do đó, ta có:
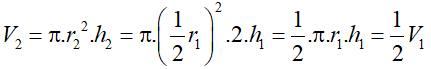
Mà V2 + V1 = 30 cm3
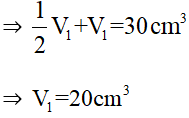
Câu 33:
Ta có:
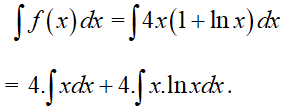
+ Tính
Đặt
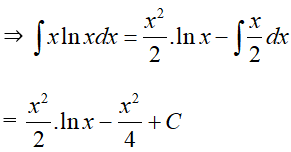
Vậy
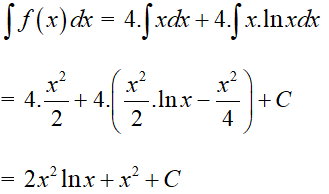
Câu 34:
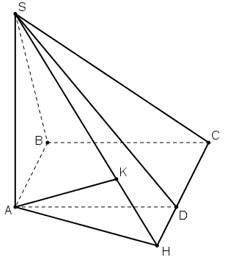
AB // CD ⇒ AB // (SCD) ⇒ d(B; (SCD)) = d(A; (SCD))
Kẻ AH ⊥ CD, AK ⊥ SH.
+ Chứng minh d(A; (SCD)) = AK.
Ta có: SA ⊥ (ABCD) ⇒ SA ⊥ CD
Mà AH ⊥ CD
⇒ CD ⊥ (SAH) ⇒ CD ⊥ AK.
Mà AK ⊥ SH
⇒ AK ⊥ (SCD)
Vậy d(A; (SCD)) = AK.
+ Tính AK:
Hình thoi ABCD có
Xét ΔADH vuông tại H có
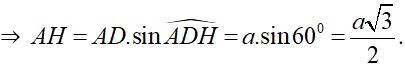
Xét ΔSAH vuông tại A, đường cao AK có:
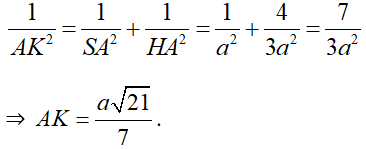
Vậy
Câu 35:
+ Tìm giao điểm của (d) và (P).
Phương trình tham số của d:
Gọi A(t; –1 + 2t; 2 – t) là giao điểm của (d) và (P)
⇒ t + 2t – 1 + 2 – t – 3 = 0 ⇒ t = 1.
Vậy A(1; 1; 1).
+ Lấy điểm B(0; –1; 2) ∈ (d). Tìm B’ là hình chiếu của B trên (P).
Gọi d’ là đường thẳng đi qua B và vuông góc với (P)
⇒ d’ nhận u→ = nP→ = (1; 1; 1) là một vtcp
⇒ Phương trình d’:
B’(t; –1 + t; 2 + t) là hình chiếu của B trên (P) ⇒ B’ = (d’) ∩ (P)
⇒ t + t – 1 + t + 2 – 3 = 0
+ Gọi Δ là hình chiếu của (d) trên (P).
Δ là đường thẳng qua A và B’
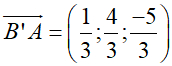
⇒ Δ nhận u→ = (1; 4; -5) là một vtcp
Δ đi qua A(1; 1; 1) nên
Câu 36:
Ta có: y’ = –3x2 – 12x + 4m – 9.
Hàm số nghịch biến trên (–∞; –1)
⇔ y’ ≤ 0 với ∀ x ∈ (–∞; –1)
⇔ –3x2 – 12x + 4m – 9 ≤ 0 ∀ x ∈ (–∞; –1)
⇔ 4m ≤ 3x2 + 12x + 9 ∀ x ∈ (–∞; –1)
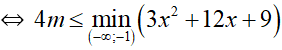
+ Xét g(x) = 3x2 + 12x + 9
g’(x) = 6x + 12
g’(x) = 0 ⇔ x = –2.
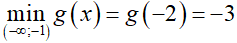
Vậy 4m ≤ –3 hay
Câu 37:
Đặt z = a + bi ⇒ z− = a - bi.
(z + 2i)(z− + 2)
= (a + bi + 2i)(a - bi + 2)
= [a + (b + 2)i].[(a + 2) - bi]
= a(a + 2) + b(b + 2) + [(a + 2)(b + 2) - ab].i
(z + 2i)(z− + 2) là số thuần ảo
⇔ a(a + 2) + b(b + 2) = 0
⇔ a2 + 2a + b2 + 2b = 0
⇔ (a + 1)2 + (b + 1)2 = 2.
Vậy tập hợp các điểm biểu diễn của z là đường tròn (x + 1)2 + (y + 1)2 = 2 có tâm (–1; –1).
Câu 38:
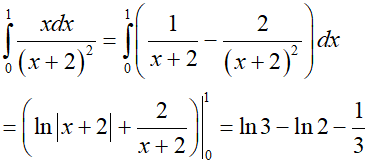
⇒ a = –1/3, b = –1, c = 1
⇒ 3a + b + c = –1.
Câu 39:
Ta có:
f(x) < ex + m ∀ x ∈ (–1; 1)
⇔ m > f(x) – ex ∀ x ∈ (–1; 1)
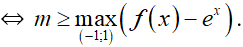
Xét g(x) = f(x) – ex.
g’(x) = f’(x) – ex.
Dựa vào bảng biến thiên ta thấy f’(x) < 0 với ∀ x ∈ (–1; 1)
⇒ g’(x) = f’(x) – ex < 0 với ∀ x ∈ (–1; 1)
⇒ g(x) nghịch biến trên (–1; 1)
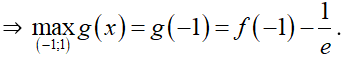
Vậy
Câu 40:
+ Không gian mẫu: n(Ω) = 6!
Gọi A : “Mỗi học sinh nam đều ngồi đối diện với một học sinh nữ”
Chọn chỗ cho học sinh nữ đầu tiên có 6 (cách)
Chọn chỗ cho học sinh nữ thứ hai (Không ngồi đối diện với học sinh nữ đầu) có 4 (cách)
Chọn chỗ cho học sinh nữ thứ ba (không ngồi đối diện với học sinh nữ đầu và thứ 2) có 2 (cách)
Xếp 3 học sinh nam vào ba chỗ còn lại có 3! (cách)
⇒ n(A) = 6.4.2.3!
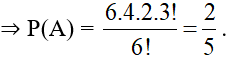
Câu 41:
Gọi I(x1; y1; z1) là điểm thỏa mãn 2IA→ + 3IB→ = 0→
⇔ 2.(2 – x1; –2 – y1; 4 – z1) + 3.(–3 – x1; 3 – y1; –1 – z1) = (0; 0; 0)
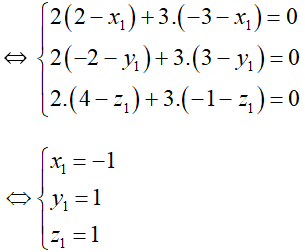
⇒ I(–1; 1; 1) ⇒ IA2 = 27 , IB2 = 12
Ta có:
2.MA2 + 3.MB2 = 2.MA→ + 3.MB→
2.(MI→ + IA→)2 + 3.(MI→ + IB→)2
= 5.MI2 + 2.MI→.(2.IA→ + 3.IB→) + 2.IA2 + 3.IB2
= 5.MI2 + 0 + 2.27 + 3.12
= 5.MI2 + 90.
Mà ta có:
Do đó 2.MA2 + 3.MB2 ≥ 5.32 + 90 = 135.
Câu 42:
Giả sử z = a = bi
⇒ z− = a - bi
Ta có: |z|2 = 2.|z + z−| + 4
⇔ |z2| = 2.|2a| + 4
⇔ a2 + b2 = 4|a| + 4 (1)
|z - 1 - i| = |z - 3 + 3i|
⇔ |(a - 1) + (b - 1)I| = |(a - 3) + (b - 3)i|
⇔ (a - 1)2 + (b - 1)2 = (a - 3)2 + (b + 3)2
⇔ a - 2b - 4 = 0
⇔ a = 2b + 4 (2)
Thế (2) vào (1) ta được:
(2b + 4)2 + b2 = 4.|2b + 4| + 4
⇔ 5b2 + 16b + 12 = 4.|2b + 4|
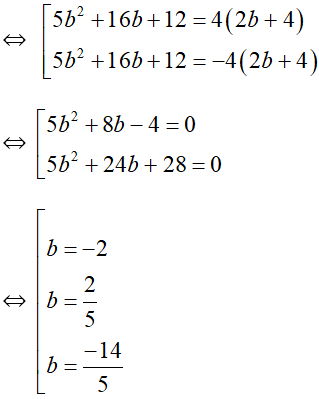
Vậy có ba số phức thỏa mãn điều kiện giả thiết.
Câu 43:
Đặt t = sin x.
x ∈ (0; π) ⇒ t ∈ (0; 1].
Phương trình f (sin x) = m có nghiệm thuộc khoảng (0; π)
⇔ phương trình f(t) = m có nghiệm t ∈ (0; 1]
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(t) và đường thẳng y = m.
Dựa vào đồ thị hàm số ta thấy: phương trình f(t) = m có nghiệm t ∈ (0; 1] khi đường thẳng y = m cắt đồ thị hàm số f trên (0; 1] hay –1 ≤ m < 1.
Câu 44:
Gọi N là số tiền vay ban đầu, r là lãi suất hàng tháng, A là số tiền ông A hoàn nợ hàng tháng.
+ Số tiền còn nợ ngân hàng sau tháng thứ nhất:
T1 = N.(1 + r) – A
+ Số tiền còn nợ ngân hàng sau tháng thứ hai:
T2 = T1.(1 + r) – A = N.(1 + r)2 - A.(1 + r) - A
+ Số tiền còn nợ ngân hàng sau tháng thứ ba:
T3 = T2(1 + r) – A = N.(1 + r)3 - A.(1 + r)2 - A(1 + r) – A
...
+ Số tiền nợ ngân hàng sau tháng thứ n:
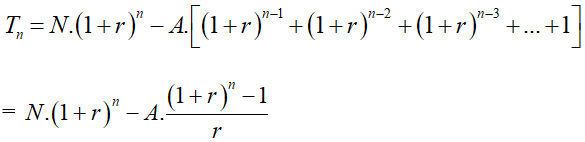
Áp dụng vào bài toán với N = 100 triệu đồng, r = 0,01.
Sau 5 năm (60 tháng), ông A trả hết nợ nên ta có:
T60 = 0
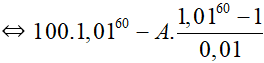
A ≈ 2,22
Câu 45:
Mặt cầu (S): (x – 3)2 + (y – 2)2 + (z – 5)2 = 36 có tâm I(3; 2; 5) và bán kính R = 6.
IE = √6 < R nên E nằm trong mặt cầu.
(P) có vecto pháp tuyến nP→ = (2; 2; -1)
+ Tìm hình chiếu H của I trên mặt phẳng (P).
Đường thẳng qua I và vuông góc với (P):
H là hình chiếu của I trên (P) nên H(3 + 2t; 2 + 2t; 5 – t).
H ∈ (P) ⇒ 2(3 + 2t) + 2(2 + 5t) – 5 + t – 3 = 0
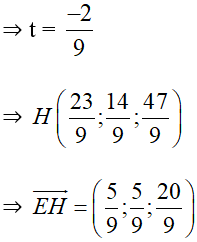
+ (Δ) đi qua E, nằm trong (P) và cắt (S) tại 2 điểm có khoảng cách nhỏ nhất
⇔ Δ đi qua E, nằm trong (P) và Δ ⊥ EH.
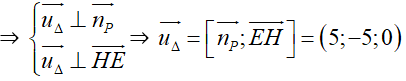
⇒ Δ cũng nhận u→ = (1; -1; 0) là vectơ chỉ phương .
Vậy phương trình đường thẳng cần tìm:
Câu 46:
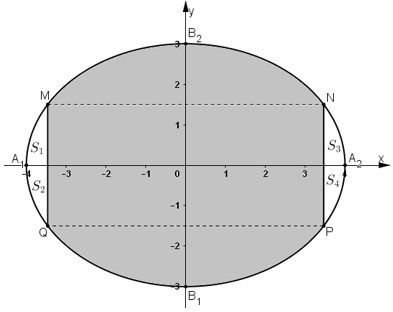
(E) có A1A2 = 8m ⇒ 2a = 8 ⇒ a = 4.
(E) có B1B2 = 6m ⇒ 2b = 6 ⇒ b = 3.
Phương trình chính tắc của elip:
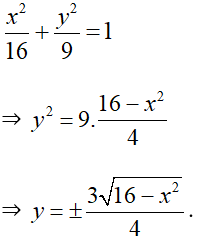
M ∈ (E), 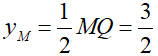
Đường thẳng MQ: x = -2√3 .
S1 là phần diện tích được giới hạn bởi (E), trục Ox và đường thẳng MQ.
Do đó
Diện tích phần không bị tô màu là: S1 + S2 + S3 + S4 ≈ 2,174
Diện tích cả elip là: S = π.a.b = 12π
Diện tích phần được tô màu là: 12π - 2,174 ≈ 35,525.
Chi phí để sơn biển quảng cáo là:
2,174.100000 + 35,525.200000 ≈ 7322000
Câu 47:
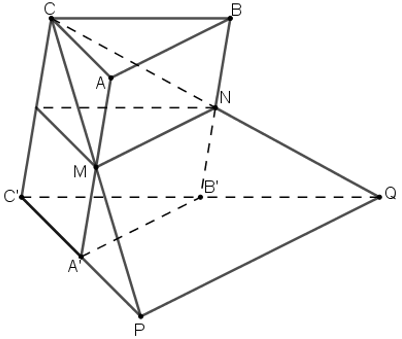
Đặt V = VABC.A'B'C'
Ta có:
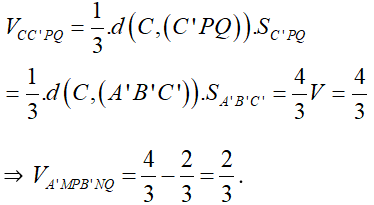
Câu 48:
y = 3.f(x + 2) – x3 + 3x đồng biến
⇔ y’ = 3. f’(x + 2) – 3x2 + 3 > 0
⇔ f’(x + 2) – x2 + 1 > 0 (1)
Đặt t = x + 2 ⇒ x = t – 2
(1) trở thành f’(t) > (t – 2)2 – 1
⇔ f’(t) > t2 – 4t + 3.
Dựa vào bảng biến thiên ta có đồ thị:
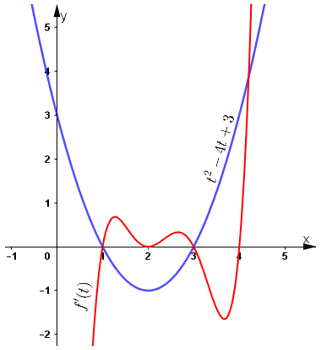
Nhìn vào đồ thị thấy:
f’(t) > t2 – 4t + 3
⇔ 1 < t < 3 hoặc t > 4
⇔ -1 < x < 1 hoặc x > 2
Trong các đáp án trên chỉ có C. thỏa mãn.
Câu 49:
Ta có: m2(x4 – 1) + m(x2 – 1) – 6(x – 1) ≥ 0 ∀ x ∈ R
⇔ m2(x2 + 1)(x – 1)(x + 1) + m(x – 1)(x + 1) – 6(x – 1) ≥ 0 ∀ x ∈ R
⇔ (x – 1)[m2(x2 + 1)(x + 1) + m(x + 1) – 6] ≥ 0 ∀ x ∈ R (1)
+ Với m = 0, (1) ⇔ -6(x – 1) ≥ 0 ∀ x ∈ R (Loại)
+ Với m ≠ 0. Đặt f(x) = m2(x2 + 1)(x + 1) + m(x + 1) – 6.
⇒ x = 1 phải là nghiệm của f(x)
⇒ 4m2 + 2m – 6 = 0
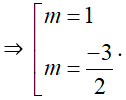
Nếu m = 1, thì f(x) = (x2 + 1)(x + 1) + (x + 1) – 6
= x3 + x2 + 2x – 4
= (x – 1)(x2 + 2x + 4)
(1) trở thành (x – 1)2 (x2 + 2x + 4) ≥ 0 ∀ x ∈ R (Thỏa mãn)
Nếu m = -3/2 thì
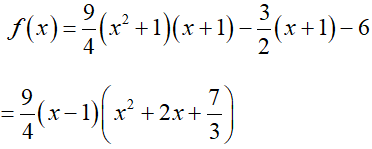
(1) trở thành 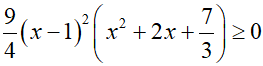
Vậy có hai giá trị của m thỏa mãn là m = 1 và m = -3/2 . Tổng của chúng bằng -1/2
Câu 50:
f(x) = mx4 + nx3 + px2 + qx + r
⇒ f’(x) = 4mx3 + 3nx2 + 2px + q.
Dựa vào đồ thị hàm số y = f’(x) ta thấy:
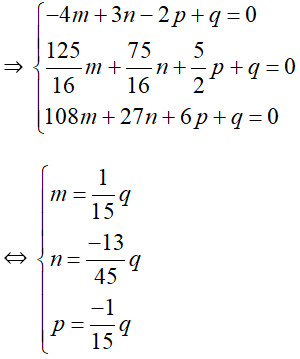
Xét f(x) = r
⇔ mx4 + nx3 + px2 + qx + r = r
⇔ mx4 + nx3 + px2 + qx = 0
⇔ x.(mx3 + nx2 + px + q) = 0
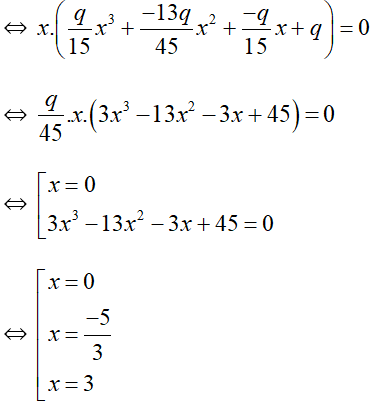
Vậy phương trình f(x) = r có ba nghiệm
Xem thử Đề thi Tốt nghiệp Toán 2025 Xem thử Đề thi Tốt nghiệp Văn 2025 Xem thử Đề thi Tốt nghiệp Anh 2025 Xem thử Đề thi Tốt nghiệp Vật Lí 2025 Xem thử Đề thi Tốt nghiệp Hóa 2025 Xem thử Đề thi Tốt nghiệp Sinh 2025 Xem thử Đề thi Tốt nghiệp Sử 2025 Xem thử Đề thi Tốt nghiệp Địa 2025 Xem thử Đề thi Tốt nghiệp KTPL 2025
Xem thêm đề thi minh họa năm 2019 các môn học có đáp án hay khác:
- Đề minh họa 2019 môn Vật lí có đáp án
- Đề minh họa 2019 môn Hóa học có đáp án
- Đề minh họa 2019 môn Ngữ văn có đáp án
- Đề minh họa 2019 môn Tiếng Anh có đáp án
- Đề minh họa 2019 môn Sinh học có đáp án
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

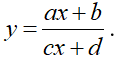
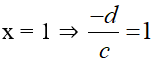
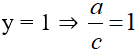
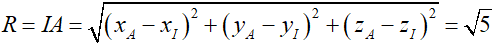
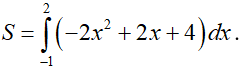
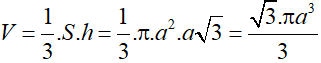
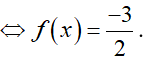
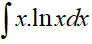
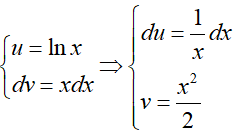
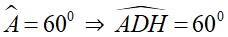
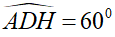
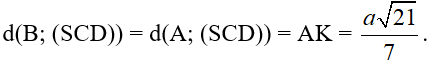
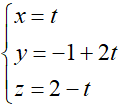
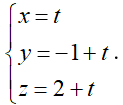
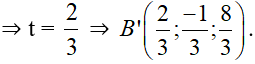
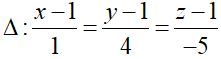
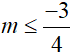
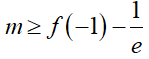
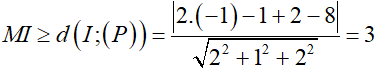
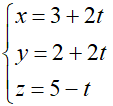
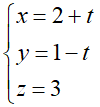
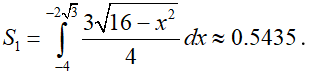
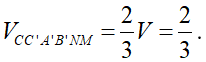
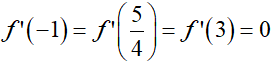



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

