[Năm 2024] Top 50 Đề thi Toán 9 Học kì 2 chọn lọc, có đáp án

---

---

[Năm 2024] Top 50 Đề thi Toán 9 Học kì 2 chọn lọc, có đáp án

Phần dưới đây liệt kê Top 50 Đề thi Toán 9 Học kì 2 năm học 2024 - 2025 chọn lọc, có đáp án. Bộ đề thi gồm các đề thi giữa học kì 2, đề thi học kì 2 biên soạn theo Thông tư 22 của Bộ Giáo dục & Đào tạo về cách đánh giá năng lực học sinh mới. Hi vọng bộ đề thi này sẽ giúp bạn ôn luyện & đạt điểm cao trong các bài thi Toán 9 Học kì 2.

Đề thi Toán 9 theo PPCT

• Bộ Đề thi Toán 9 Giữa kì 2 năm 2024 (15 đề)

• Bộ Đề thi Toán 9 Học kì 2 năm 2024 (15 đề)

• Đề thi Toán 9 Giữa học kì 2 có đáp án (10 đề)
• Đề thi Toán 9 Học kì 2 có đáp án (10 đề)

Lưu trữ: Đề thi Toán 9 theo Chương

• Đề kiểm tra Toán 9 Chương 3 Đại số có đáp án (10 đề)
• Đề kiểm tra Toán 9 Chương 4 Đại số có đáp án (9 đề)
• Đề kiểm tra Toán 9 Chương 3 Hình học có đáp án (8 đề)
• Đề kiểm tra Toán 9 Chương 4 Hình học có đáp án (10 đề)

---

---

---

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa học kì 2

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

Bài 1 (2,5 điểm)

          Trong mặt phẳng tọa độ Oxy, cho Parabol 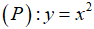và đường thẳng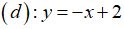

1. Tìm tọa độ giao điểm của (P) và (Q).
2. Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB,

Bài 2 (2,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

          Trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy. Đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy. Tính số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu.

Bài 3 (4,0 điểm)

          Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng  A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.

1. Chứng minh tứ giác BMFE nội tiếp.
2. Chứng minh BF vuông góc với AK và EK.EF = EA.EB
3. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.

Bài 4. (1,0 điểm) Với các số a, b, c > 0 và thỏa mãn a + b + c = 1

Chứng minh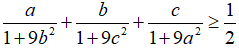

Đáp án và hướng dẫn giải

Câu 1:

a. Hoành độ giao điểm của (P) và (Q) là nghiệm của phương trình:

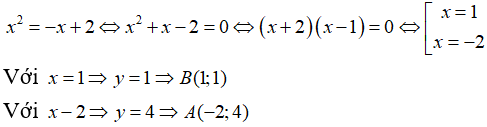
b. Gọi A, B là hai giao điểm của (P) và )Q). Tính diện tích tam giác OAB.

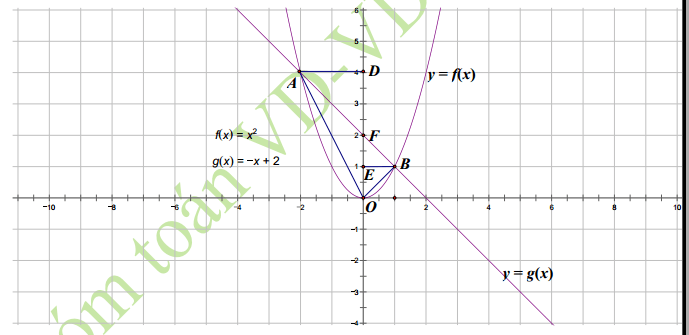
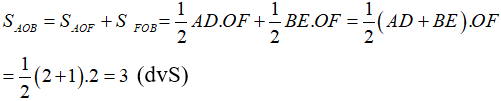
Câu 2:

Gọi số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu là x, y (, chi tiết máy)

Vì trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy nên ta có phương trình:

Vì đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy, nên ta có phương trình:

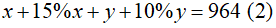
Từ (1) và (2) ta có hệ phương trình:

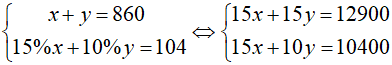
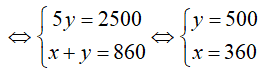
Vậy trong tháng đầu, số chi tiết máy mỗi tổ đã sản xuất được lần lượt là: 360 và 500.

Câu 3:

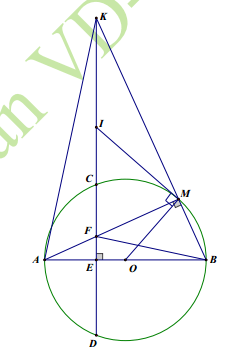
a. Chứng minh tứ giác BMFE nội tiếp.

Ta có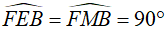

Nên 4 điểm E, F, M, B cùng thuộc đường tròn đường kính BF, suy ra tứ giác BMFE nội tiếp.

b. Chứng minh BF vuông góc với AK và EK.EF = EA.EB

Nên F là trực tâm, suy ra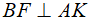

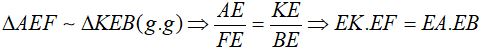
c. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.

Ta có:

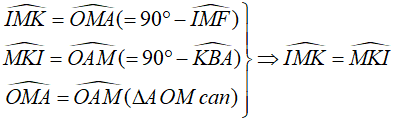
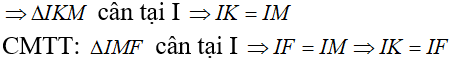
Câu 4:

Ta có:

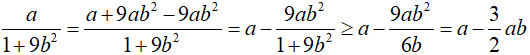
CMTT:

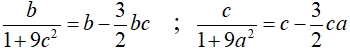
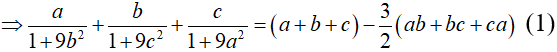
Mặt khác:

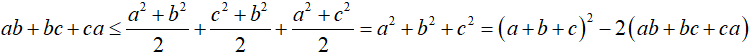
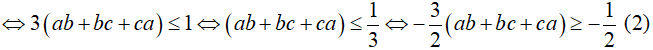
Từ (1) và (2)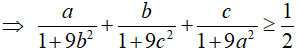 

Dấu “=” xảy ra khi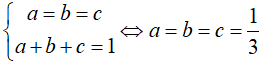 

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 2

Môn: Toán lớp 9

Thời gian làm bài: 90 phút

Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình sau:

a) 3x² – 7x + 2 = 0

b) x⁴ – 5x + 4 = 0

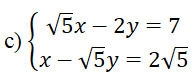
Bài 2: (1,5 điểm)

a) Vẽ đồ thị (P) hàm số y= x²/4

b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B

Bài 3: (1,5 điểm) Cho phương trình (ẩn x) : x² – 2mx – 4m – 4 = 0(1)

a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.

b) Tìm m để phương trình (1) có 2 nghiệm x₁, x₂ thỏa mãn x₁² + x₂² - x₁x₂ = 13

Bài 4: (1 điểm) Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m2.

Bài 5: (3,5 điểm) Cho đường tròn (O;R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).

a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC

b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.

c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.

d) Tính theo R diện tích tam giác BDC.

Đáp án và Hướng dẫn giải

Bài 1:

a) 3x² – 7x + 2 = 0

Δ= 7² -4.3.2 = 49 - 24 = 25 > 0 ⇒ √Δ = 5

Phương trình có 2 nghiệm phân biệt:

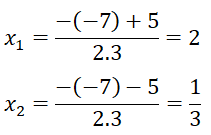
Vậy tập nghiệm của phương trình là S = {2; 1/3}

b) x⁴ - 5x² + 4 = 0

Đặt t = x² ≥ 0 , ta có phương trình:

t² - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)

t₁ = 1 (nhận) ; t₂ = 4 (nhận)

với t = 1 ⇔ x² = 1 ⇔ x = ± 1

với t = 4 ⇔ x² = 4 ⇔ x = ± 2

Vậy nghiệm của phương trình x = ±1; x = ± 2

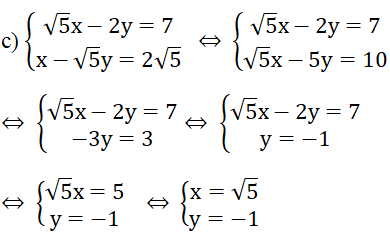
Vậy hệ phương trình có nghiệm (x; y) = ( √5; -1)

Bài 2:

a) Tập xác định của hàm số: R

Bảng giá trị:

x	-4	-2	0	2	4
y = x2 / 4	4	1	0	1	4

Đồ thị hàm số y = x² / 4 là một đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.

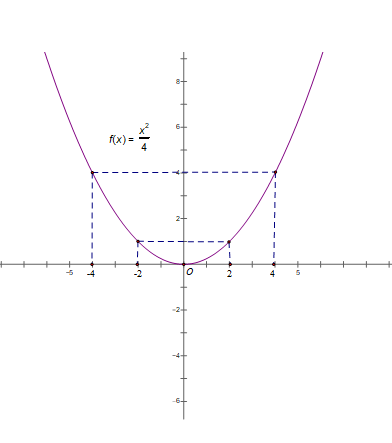
b) Với x = 4, ta có: y = x²/4 = 4 ⇒ A (4; 4)

Với x = 2, ta có y = x²/4 = 1 ⇒ B ( 2; 1)

Giả sử đường thẳng đi qua 2 điểm A, B là y = ax + b

Đường thẳng đi qua A (4; 4) nên 4 = 4a + b

Đường thẳng đi qua B (2; 1) nên : 1= 2a + b

Ta có hệ phương trình

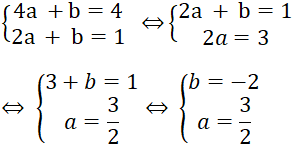
Vậy phương trình đường thẳng đi qua 2 điểm A, B là y = 3/2 x - 2

Bài 3:

a) Δ' = m² - (-4m - 4) = m² + 4m + 4 = (m + 2)² ≥ 0 ∀m

Vậy phương trình đã cho luôn có nghiệm với mọi m

b) Gọi x₁ ; x₂ lần lượt là 2 nghiệm của phương trình đã cho

Theo hệ thức Vi-et ta có:

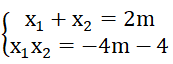
x₁² + x₂² -x₁ x₂ = (x₁ + x₂ )² - 3x₁ x₂ = 4m² + 3(4m + 4)

Theo bài ra: x₁² + x₂² - x₁ x₂=13

⇒ 4m² + 3(4m + 4) = 13 ⇔ 4m² + 12m - 1 = 0

Δ_m = 12² -4.4.(-1) = 160 ⇒ √(Δ_m ) = 4√10

Phương trình có 2 nghiệm phân biệt

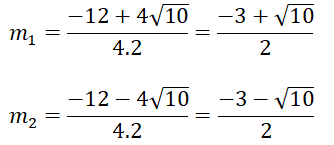
Vậy với 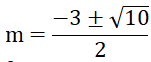thì phương trình có 2 nghiệm x₁; x₂ thỏa mãn điều kiện x₁² + x₂² - x₁ x₂ = 13

Bài 4:

Gọi chiều rộng của hình chữ nhật là x (m) ( x > 0 )

⇒ Chiều dài của hình chữ nhật là x + 3 (m)

Khi đó diện tích của hình chữ nhật là x(x + 3) (m² )

Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70m² nên ta có phương trình:

(x + 2)(x + 3 + 2) = x(x + 3) + 70

⇔ (x + 2)(x + 5) = x(x + 3) + 70

⇔ x² + 7x + 10 = x² + 3x + 70

⇔ 4x = 60

⇔ x = 15

Vậy chiều rộng của hình chữ nhật là 15m

Chiều dài của hình chữ nhật là 18m

Bài 5:

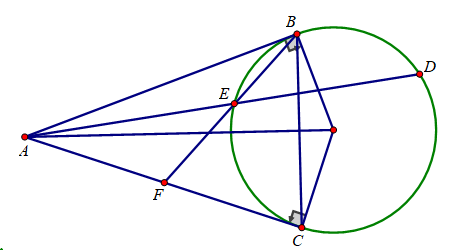
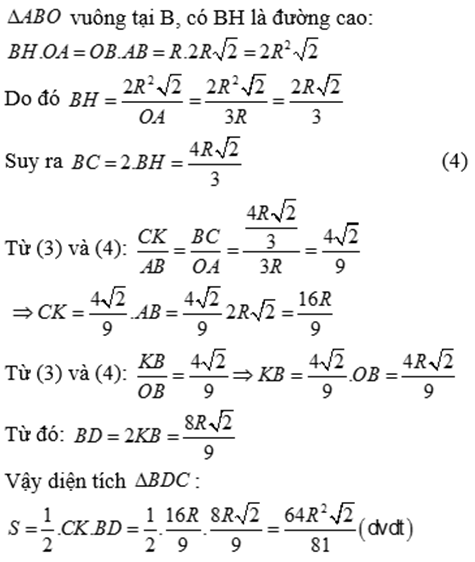
Phòng Giáo dục và Đào tạo .....

Đề kiểm tra 15 phút chương 3 đại số Học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 15 phút

Đề bài

Câu 1: (6 điểm) Giải các hệ phương trình sau:

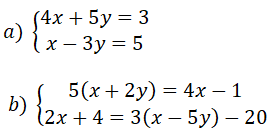
Câu 2: (4 điểm) Tìm giá trị của a và b để hai đường thẳng (d₁ ) ∶(3a - 1)x + 2by = 56 và (d₂ ):1/2 ax - (3b + 2)y = 3 cắt nhau tại điểm M(2; -5).

Hướng dẫn giải

Câu 1:

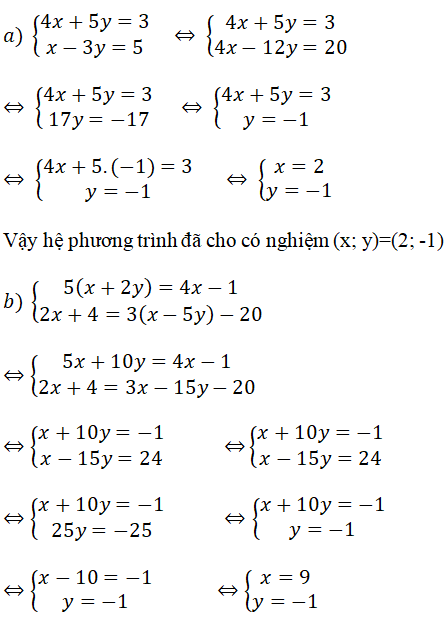
Vậy hệ phương trình đã cho có nghiệm (x; y) = (9; -1).

Câu 2:

Hai đường thẳng (d₁ ) và (d₂ ) cắt nhau tại M(2; -5) nên:

M ∈ (d₁ ): (3a - 1)² + 2b.(-5) = 56 ⇔ 6a - 10b = 58

M ∈ (d₂ ): 1/2 a.2 - (3b + 2)(-5) = 3 ⇔ a + 15b = -7

Khi đó, ta có hệ phương trình:

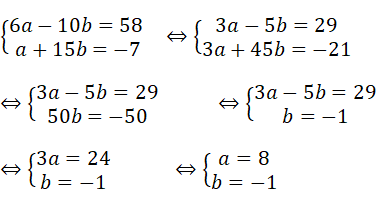
Vậy a = 8 và b = -1 thì hai đường thẳng (d₁ ) và (d₂ ) cắt nhau tại M(2; -5).

Phòng Giáo dục và Đào tạo .....

Đề kiểm tra 15 phút chương 4 đại số Học kì 1

Môn: Toán lớp 9

Thời gian làm bài: 15 phút

Đề bài

Câu 1: (6 điểm) Giải các phương trình sau:

a) 4x² - 20 = 0

b) x² - (√5 + √2)x + √10 = 0

Câu 2: (4 điểm) Cho phương trình x² - 3x + m - 5 = 0. Tìm m để phương trình có 2 nghiệm phân biệt x₁; x₂ thỏa mãn điều kiện x₁ x₂=4

Hướng dẫn giải

Câu 1:

a)4x² - 20 = 0

a = 4; b = 0; c = -20

Δ = b² - 4ac = 0 - 4.4(-20) = 320 > 0 ⇒ √Δ = 8√5

Phương trình có hai nghiệm phân biệt:

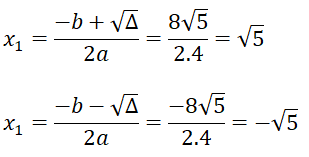
Vậy tập nghiệm của phương trình là S = {√5; -√5}

b)x² - (√5 + √2)x + √10 = 0

a = 1; b = √5 + √2 ; c = √10

Δ = b² - 4ac = (√5 + √2)² - 4.1.√10 = 5 + 2√10 + 2 - 4√10

= 5 - 2√10 + 2 = (√5 - √2)² > 0

⇒ √Δ = √5 - √2

Phương trình đã cho có 2 nghiệm phân biệt

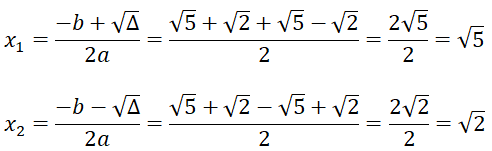
Vậy tập nghiệm của phương trình là S = {√5; -√2}

Câu 2: x² - 3x + m - 5 = 0

a = 1; b = -3; c = m – 5

Δ = b² - 4ac = (-3)² - 4(m - 5) = 29 - 4m

Phương trình có 2 nghiệm phân biệt x₁; x₂ khi và chỉ khi

Δ > 0 ⇔ 29 - 4m > 0 ⇔ m < 29/4

Theo định lí Vi-et ta có:

x₁x₂ = c/a = m - 5

Theo bài ra

x₁x₂ = 4 ⇔ m - 5 = 4 ⇔ m = 9 (Không TMĐK m < 29/4)

Vậy không tồn tại m thỏa mãn đề bài.

Xem thêm các đề kiểm tra, Đề thi Toán 9 chọn lọc, có đáp án hay khác:

• Top 45 Đề kiểm tra Toán lớp 9 Học kì 1 có đáp án

---

---

---