Top 50 Đề thi Toán 9 Học kì 2 năm 2026 (cấu trúc mới, có đáp án)
Trọn bộ 50 đề thi Toán 9 Học kì 2 theo cấu trúc mới sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều có đáp án và ma trận sẽ giúp bạn ôn tập và đạt điểm cao trong bài thi Toán 9.
Top 50 Đề thi Toán 9 Học kì 2 năm 2026 (cấu trúc mới, có đáp án)
Xem thử Đề thi CK2 Toán 9 KNTT Xem thử Đề thi CK2 Toán 9 CTST Xem thử Đề thi CK2 Toán 9 CD
Chỉ từ 150k mua trọn bộ đề thi Toán 9 Học kì 2 theo cấu trúc mới bản word có lời giải chi tiết, dễ dàng chỉnh sửa:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Đề thi Toán 9 Học kì 2 (Giáo viên VietJack)
Đề thi Học kì 2 Toán 9 (theo bộ sách)
Đề thi Học kì 2 Toán 9 (trên cả nước)
Đề thi Học kì 2 Toán 9 trường THCS Ngọc Thụy (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Phúc Đồng (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Ngọc Lâm (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Hà Đông (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Gia Lâm (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Hoài Đức (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường M.V. Lômônôxốp (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Thạch Thất (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Ba Đình (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THPT chuyên Hà Nội – Amsterdam năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Hai Bà Trưng (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS thị trấn Văn Điển (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Chu Văn An (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Cầu Giấy (Hà Nội) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Võ Trường Toản (Bà Rịa - Vũng Tàu) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Phước Bửu (Bà Rịa - Vũng Tàu) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Hoàng Hoa Thám (Tp.HCM) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Bình Tân (Tp.HCM) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Tân Phú (Tp.HCM) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Bàn Cờ (Tp.HCM) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Kiến Thiết (Tp.HCM) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Bình Thạnh (Tp.HCM) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Quận 7 (Tp.HCM) năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT TP Hải Dương năm 2024-2025
Đề thi Học kì 2 Toán 9 phòng GD&ĐT Hoàng Mai (Nghệ An) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Ông Ích Đường (Đà Nẵng) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Nguyễn Đình Chiểu (Đà Nẵng) năm 2024-2025
Đề thi Học kì 2 Toán 9 trường THCS Đỗ Đăng Tuyển (Đà Nẵng) năm 2024-2025
Xem thử Đề thi CK2 Toán 9 KNTT Xem thử Đề thi CK2 Toán 9 CTST Xem thử Đề thi CK2 Toán 9 CD
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2 - Kết nối tri thức
năm 2026
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Đồ thị của hàm số x2 + 2(m + 3)x + m2 + 6m = 0 có trục đối xứng là
A. trục Ox.
B. đường thẳng y = -x.
C. đường thẳng y = x.
D. trục Oy.
|
Câu 2. Cho hàm số y = ax2 có đồ thị như hình vẽ bên. Hàm số đó là A. y = −x2. B. y = −2x2. C. y = 2x2. D. y = x2. |
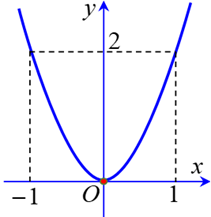 |
Câu 3. Phương trình bậc hai x2 - 3x + 7 = 0 có biệt thức ∆ bằng
A. 2.
B. −19.
C. −37.
D. 16.
Câu 4. Phương trình nào sau đây có hai nghiệm trái dấu?
A. x2 – 6x + 5 = 0.
B. x2 – 5x + 6 = 0.
C. –x2 – 6x – 5 = 0.
D. x2 – 5x – 6 = 0.
Câu 5. Trục ngang của biểu đồ tần số tương đối ghép nhóm dạng cột xác định
A. tần số tương đối của nhóm số liệu.
B. đơn vị độ dài phù hợp với các tần số tương đối.
C. các nhóm số liệu cần biểu diễn.
D. tiêu đề cho biểu đồ.
Câu 6. Bảng thống kê sau cho biết số lượt mượn các loại sách trong một tuần tại thư viện của một trường Trung học cơ sở như sau:
|
Loại sách |
Sách giáo khoa |
Sách tham khảo |
Truyện ngắn |
Tiểu thuyết |
|
Số lượt |
20 |
80 |
70 |
30 |
Từ bảng thống kê, tần số tương đối về số lượng sách giáo khoa được mượn là
A. 10%.
B. 15%.
C. 35%.
D. 40%.
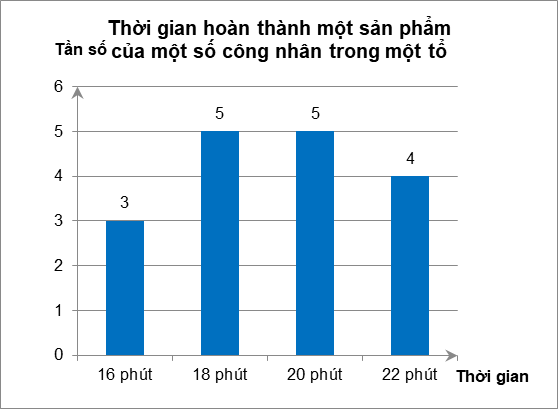
Câu 7. Thời gian hoàn thành một sản phẩm (tính bằng phút) của một số công nhân trong một tổ được biểu diễn ở biểu đồ dưới đây:
Thời gian hoàn thành một sản phẩm của công nhân chủ yếu là
A. 5 phút.
B. 17 phút.
C. 18 phút và 20 phút.
D. 20 phút và 22 phút.
Câu 8. Khi gieo hai con xúc xắc cân đối và đồng chất, gọi T là tổng số chấm trên hai con xúc xắc thì kết quả nào sau đây không thể xảy ra?
A. T = 1.
B. T = 2.
C. T = 3.
D. T = 4.
Câu 9. Khẳng định nào sau đây là sai?
A. Góc nội tiếp của đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn.
B. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của cung bị chắn.
C. Trong một đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
D. Trong một đường tròn, góc nội tiếp chắn cung nhỏ có số đo bằng số đo của góc ở tâm chắn cùng một cung.
Câu 10. Tâm đường tròn nội tiếp của một tam giác là giao của các đường
A. trung trực.
B. phân giác trong.
C. phân giác ngoài.
D. đường cao.
Câu 11. Khi tứ giác MNPQ nội tiếp đường tròn, và có . Khi đó, góc P bằng
A. 90°.
B. 180°.
C. 110°.
D. 120°.
Câu 12. Cho tam giác ABC đều nội tiếp đường tròn (O). Các phép quay giữ nguyên tam giác ABC là
A. .
B. .
C. .
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Cho phương trình 2x2 + (2m - 1)x + m - 1 = 0 với m là tham số, .
a) Phương trình đã cho là phương trình bậc hai một ẩn.
b) Phương trình luôn có hai nghiệm x1, x2 với mọi .
c) Tổng và tích hai nghiệm của phương trình lần lượt là ; .
d) Có một giá trị của m để phương trình có hai nghiệm x1, x2 thoả mãn .
Câu 14. Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính 50 cm, phần gạo vun lên có dạng hình nón cao 15 cm.
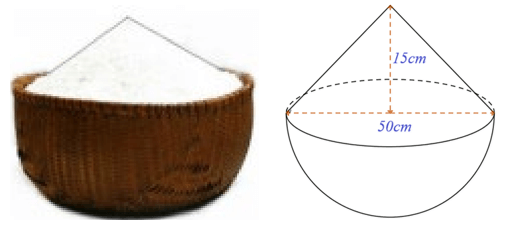
Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5 cm, chiều cao 15 cm) để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm 90% thể tích lon.
a) Thể tích hình cầu có bán kính đáy R, được tính bằng công thức: .
b) Phần gạo nằm ngang mặt thúng trở xuống có dạng nửa hình cầu có bán kính 50 cm.
c) Thể tích phần gạo trong thúng là (cm3).
d) Với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là 15 ngày.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Hai đội công nhân đắp đê ngăn triều cường. Nếu hai đội cùng làm thì trong 6 ngày xong việc. Nếu làm riêng thì đội I hoàn thành công việc nhanh hơn đội II là 9 ngày. Hỏi nếu làm riêng thì đội I đắp xong đê trong bao nhiêu ngày?
Câu 16. Tập hợp A có 24 số chia hết cho 5 và một số số không chia hết cho 5. Bạn An chọn ngẫu nhiên một số từ tập hợp A. Biết rằng xác suất của biến cố “Chọn được số không chia hết cho 5” là 0,7. Hỏi tập hợp A có bao nhiêu phần tử?
Câu 17. Cho tứ giác nội tiếp ABCD đường tròn (O). Hai đường thẳng AB và DC cắt nhau tại X. Biết . Tính số đo góc BXC (đơn vị độ).
|
Câu 18. Nón Huế là một hình nón có đường kính đáy bằng 40 cm, độ dài đường sinh là 30 cm Người ta lát mặt xung quanh hình nón bằng ba lớp lá khô. Tính diện tích lá cần dùng để tạo nên một chiếc nón Huế như vậy (kết quả làm tròn đến hàng đơn vị với đơn vị cm2). |
 |
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm)
1. Ghi lại cự li ném tạ (đơn vị: mét) của một vận động viên sau đợt tập huấn đặc biệt trong bảng sau:
|
20 |
20,5 |
20,64 |
20,35 |
20,65 |
20,4 |
20,67 |
20,8 |
|
20,7 |
20,45 |
20,72 |
20,5 |
20,85 |
20,2 |
21,1 |
20,9 |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số ghép nhóm hay tần số không ghép nhóm? Vì sao?
b) Hãy lập bảng số liệu làm 6 nhóm trong đó nhóm đầu tiên cự li là từ 20 đến dưới 20,2 m. Lập bảng tần số và tần số tương đối ghép nhóm.
2. Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4;...; 51; 52 hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố A: “Số xuất hiện trên thẻ được rút ra là số nhỏ hơn 27”.
Bài 2. (1,5 điểm) Cho đường tròn (O), bán kính R (R > 0) và dây cung BC cố định. Một điểm A chuyển động trên cung lớn BC sao cho tam giác ABC có ba góc nhọn. Kẻ các đường cao AD, BE của tam giác ABC cắt nhau tại H và BE cắt đường tròn (O) tại F (F khác B).
a) Chứng minh rằng tứ giác DHEC nội tiếp.
b) Kẻ đường kính AM của đường tròn (O) và OI vuông góc với BC tại I. Chứng minh I là trung điểm của HM và tính AF biết BC = .
c) Khi BC cố định, xác định vị trí của A trên đường tròn (O) để DH . DA lớn nhất.
-----HẾT-----
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2 - Chân trời sáng tạo
năm 2026
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Giá trị của m để hàm số y = (2 - m)x2 (m ≠ 2) nghịch biến với mọi giá trị của x > 0 là
A. m < −2.
B. m < 2.
C. m > −2.
D. m > 2.
Câu 2. Cho parabol (P): và đường thẳng (d): . Tọa độ giao điểm của đường thẳng (d) và parabol (P) là
A. .
B. (1; 2).
C. .
D. (2; 1).
Câu 3. Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức ∆ = b2 - 4ac. Phương trình đã cho vô nghiệm khi
A. ∆ < 0.
B. ∆ > 0.
C. ∆ ≥ 0.
D. ∆ ≤ 0.
Câu 4. Hai số u, v có tổng và tích lần lượt là 32 và 231. Khi đó u và v là nghiệm của phương trình nào dưới đây?
A. x2 – 231x – 32 = 0.
B. x2 + 32x + 231 = 0.
C. x2 – 32x + 231 = 0.
D. x2 – 231x + 32 = 0.
Câu 5. Công thức tính giá trị đại diện của nhóm là
A. .
B. .
C. .
D. .
Câu 6. Cho bảng tần số ghép nhóm:
|
Nhóm |
[7; 13) |
[13; 19) |
[19; 25) |
[25; 31) |
|
Tần số |
5 |
10 |
20 |
15 |
Mệnh đề sai là mệnh đề
A. Tần số của nhóm là 15.
B. Tần số tương đối ghép nhóm của nhóm [7; 13) là 10%.
C. Tần số tương đối ghép nhóm của nhóm [13; 19) là 20%.
D. Tần số tương đối ghép nhóm của nhóm [19; 25) là 30%.
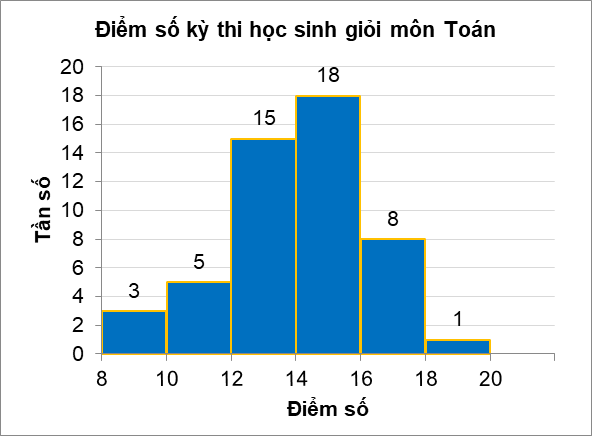
Câu 7. Trong một kỳ thi học sinh giỏi Toán (thang điểm 20) của 50 học sinh, kết quả được cho bởi biểu đồ sau:
Tần số của nhóm thí sinh có điểm thi thấp nhất là
A. 1.
B. 3.
C. 5.
D. 18.
Câu 8. Thống kê thời gian của 78 chương trình quảng cáo trên Đài truyền hình tỉnh X có 38 chương trình quảng cáo từ 10 đến 17 giây. Xác suất thực nghiệm của biến cố trên là
A. .
B. .
C. .
D. .
Câu 9. Khẳng định nào sau đây là sai?
A. Trọng tâm của tam giác đều vừa là tâm đường tròn ngoại tiếp, vừa là tâm đường tròn nội tiếp tam giác đều đó.
B. Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác của tam giác đó.
C. Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
D. Đường tròn ngoại tiếp một tam giác là đường tròn đi qua nhiều nhất là ba đỉnh của tam giác đó.
Câu 10. Góc nội tiếp nhỏ hơn hoặc bằng 90° có số đo
A. bằng nửa số đo góc ở tâm cùng chắn một cung.
B. bằng số đo của góc ở tâm cùng chắn một cung.
C. bằng số đo cung bị chắn.
D. bằng nửa số đo cung lớn.
Câu 11. Khi quay thuận chiều α° tâm O điểm A thành điểm B thì điểm A tạo thành cung AB có số đo bằng
A. α°.
B. −α°.
C. 90° − α°.
D. 180° − α°.
Câu 12. Số cạnh của đa giác đều có số đường chéo bằng số cạnh là
A. 5.
B. 6.
C. 7.
D. 8.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Cho phương trình 2x2 – 3x + 2 = 0.
a) Phương trình đã cho có hệ số a = 2; b = 3; c = 1.
b) Tổng các hệ số a, b, c là 0.
c) Phương trình đã cho có hai nghiệm đều dương.
d) Tích hai nghiệm của phương trình đã cho là 1.
|
Câu 14. Một cái ly thủy tinh (như hình vẽ), phần phía trên là hình nón có chiều cao 7cm, có đáy đường tròn bán kính 4cm. Biết trong ly đang chứa rượu với mức rượu đang cách miệng ly là 3cm. a) Thể tích hình nón có bán kính đáy R và chiều cao h, được tính bằng công thức: . b) Chiều cao của phần rượu có trong ly là 4cm.
|
 |
c) Thể tích của cái ly thủy tinh là cm3.
d) Tỉ số giữa thể tích của phần còn lại trong ly rượu so với thể tích ly là .
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Để chở 15 tấn thiết bị phục vụ Lễ kỷ niệm 70 năm chiến thắng Điện Biên Phủ, một đội vận chuyển dự định sử dụng các xe tải loại nhỏ. Do thay đổi kế hoạch, đội vận chuyển quyết định chỉ sử dụng các xe tải loại lớn. Vì vậy, số xe sử dụng giảm đi hai xe so với dự định và mỗi xe tải loại lớn chở nhiều hơn mỗi xe tải loại nhỏ là 2 tấn. Biết mỗi xe tải cùng loại đều chở số tấn thiết bị bằng nhau. Hỏi đội vận chuyển sử dụng bao nhiêu xe tải loại lớn?
Câu 16. Một hộp chứa 4 tấm thẻ cùng loại được đánh số 1; 4; 7; 9. Bạn Khuê và bạn Hương lần lượt mỗi người lấy ra 1 tấm thẻ từ hộp. Tính xác suất của biến cố A: “Số ghi trên tấm thẻ của bạn Khuê nhỏ hơn số ghi trên tấm thẻ của bạn Hương” (viết kết quả dưới dạng số thập phân).
|
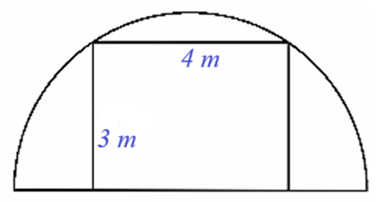
Câu 17. Người ta cần xây dựng một khung cổng hình chữ nhật rộng 4m và cao 3m, bên ngoài khung cổng được bao bởi một khung thép dạng nửa hình tròn (như hình vẽ). Chiều dài của đoạn thép dùng để làm khung nửa đường tròn đó là bao nhiêu? (làm tròn kết quả đến hàng phần mười). |
|
|
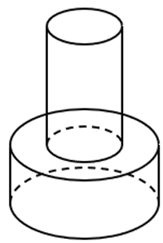
Câu 18. Một khối đồ chơi gồm hai khối trụ (H1), (H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là r1, h1, r2, h2 thỏa mãn , h2 = 2h1 (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng 30 cm3. Tính thể tích khối trụ (H1). |
|
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm)
1. Kết quả nhảy xa của một lớp (đơn vị mét) được cho trong bảng sau:
|
2,4 |
3,1 |
2,7 |
2,8 |
3,2 |
2,8 |
4,1 |
3,2 |
|
2,1 |
3,2 |
2,1 |
3,2 |
2,3 |
2,5 |
2,6 |
3,3 |
|
3,6 |
2,0 |
2,0 |
2,7 |
3,1 |
2,3 |
4,3 |
3,9 |
|
3,9 |
3,5 |
3,6 |
3,7 |
2,7 |
3,5 |
3,5 |
2,4 |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số ghép nhóm hay tấn số không ghép nhóm? Vì sao?
b) Hãy lập bảng số liệu làm 5 nhóm trong đó nhóm cuối cùng cự li là từ 4,0 đến dưới 4,5 m. Lập bảng tần số và tần số tương đối ghép nhóm.
2. Cho hai túi I và II mỗi túi chứa 3 tấm thẻ được đánh số 2; 3; 4. Rút ngẫu nhiên từ mỗi túi ra 1 tấm thẻ và ghép thành số có hai chữ số với chữ số trên tấm thẻ rút từ túi I là chữ số hàng chục. Tính xác suất của biến cố “Số tạo thành là số chia hết cho 3”.
Bài 2. (1,5 điểm) Cho đường tròn (O; R). Từ A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kỳ (M khác A) kẻ cát tuyến MNP. Gọi K là trung điểm của NP, kẻ tiếp tuyến MB. Kẻ AC ⊥ MB, BD ⊥ AM (C ∈ MB, D ∈ AM). Gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.
a) Chứng minh tứ giác AMBO nội tiếp.
b) Chứng minh OI . OM = R2 và OI . IM = IA2.
c) Chứng minh ba điểm O, H, M thẳng hàng.
-----HẾT-----
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2 - Cánh diều
năm 2026
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Trong biểu đồ hình quạt tròn, nửa đường tròn biểu diễn
A. 25%.
B. 50%.
C. 75%.
D. 100%.
Câu 2. Công thức tính giá trị đại diện của nhóm là
A. .
B. .
C. .
D. .
Câu 3. Thời gian hoàn thành một sản phẩm (tính bằng phút) của một số công nhân trong một tổ được biểu diễn ở biểu đồ dưới đây:
Thời gian hoàn thành một sản phẩm của công nhân chủ yếu là
A. 5 phút.
B. 17 phút.
C. 18 phút và 20 phút.
D. 20 phút và 22 phút.
Câu 4. Thống kê thời gian của 78 chương trình quảng cáo trên Đài truyền hình tỉnh X có 38 chương trình quảng cáo từ 10 đến 17 giây. Xác suất thực nghiệm của biến cố trên là
A. .
B. .
C. .
D. .
Câu 5. Giá trị của m để hàm số y = (2 - m)x2 (m ≠ 2) nghịch biến với mọi giá trị của x > 0 là
A. m < −2.
B. m < 2.
C. m > −2.
D. m > 2.
Câu 6. Cho parabol (P): và đường thẳng (d): . Tọa độ giao điểm của đường thẳng (d) và parabol (P) là
A. .
B. (1; 2).
C. .
D. (2; 1).
Câu 7. Phương trình nào dưới đây là phương trình bậc hai một ẩn?
A. .
B. .
C. .
D. .
Câu 8. Gọi x1, x2 là hai nghiệm của phương trình 2x2 + 11x + 7 = 0, khi đó ta có
A. .
B. .
C. .
D. .
Câu 9. Đường tròn nội tiếp hình vuông cạnh a có bán kính là
A. .
B. .
C. .
D. .
Câu 10. Trong các phát biểu sau, phát biểu nào đúng?
A. Mọi tứ giác luôn nội tiếp đường tròn.
B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 90°.
C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng 180°.
D. Tất cả các hình thang đều là tứ giác nội tiếp.
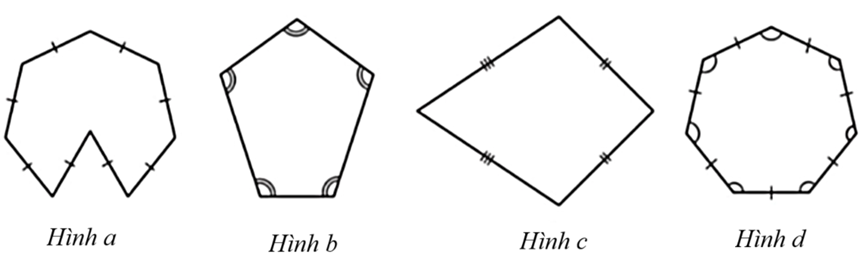
Câu 11. Cho các hình vẽ:
Trong các hình trên, hình nào là đa giác đều?
A. Hình a.
B. Hình b.
C. Hình c.
D. Hình d.
Câu 12. Cho tam giác ABC vuông tại B và góc tại A bằng 60°. Về phía ngoài tam giác vẽ tam giác đều ACD. Phép quay tâm A góc 60° biến BC thành
A. AD.
B. DK với K là trung điểm của AC.
C. CJ với J là trung điểm của AD.
D. AI với I là trung điểm của CD.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Cho phương trình 2x2 + (2m - 1)x + m - 1 = 0 với m là tham số, .
a) Phương trình đã cho là phương trình bậc hai một ẩn.
b) Phương trình luôn có hai nghiệm x1, x2 với mọi .
c) Tổng và tích hai nghiệm của phương trình lần lượt là ; .
d) Có một giá trị của m để phương trình có hai nghiệm x1, x2 thoả mãn .
|
Câu 14. Một quầy hàng A đựng bắp rang bơ vào một loại hộp có dạng hình nón với kích thước như hình vẽ. Quầy hàng B đựng bắp rang bơ vào một loại hộp có dạng hình trụ có đáy và chiều cao bằng với loại hộp hình nón mà quầy A đã dùng. Biết giá 1 hộp bắp rang bơ của quầy A và quầy B bán lần lượt là 50 000 đồng và 100 000đồng. a) Diện tích xung quanh của hình nón có bán kính đáy R và đường sinh l, được tính bằng công thức: . b) Độ dài đường sinh là cm. c) Diện tích xung quanh của hộp đựng bắp rang bơ là cm2. d) Bạn An nên mua bắp rang bơ ở quầy B để có lợi hơn. |
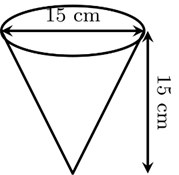 |
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Tập hợp A có 30 số chẵn và một số số lẻ. Bạn An chọn ngẫu nhiên một số từ tập hợp A. Biết rằng xác suất của biến cố “Chọn được số chia hết cho 2” là 0,4. Hỏi tập hợp A có bao nhiêu phần tử?
Câu 16. Cho đường thẳng (d): y = 2mx + 2m – 3 (m là tham số) và parabol (P): y = x2. Hỏi có bao nhiêu giá trị của m để đường thẳng (d) tiếp xúc với (P)?
Câu 17. Cho bát giác đều ABCDEFGH có tâm O. Hỏi phép quay thuận chiều tâm O góc bao nhiêu độ để biến điểm D của bát giác đều ABCDEFGH thành điểm G?
|
Câu 18. Một bình hình trụ có đường kính đáy 1 dm, chiều cao 0,8 dm bên trong có chứa viên bi hình cầu có bán kính 3 cm. Hỏi phải đổ vào bình bao nhiêu lít nước để nước đầy bình? (làm tròn đến chữ số thập phân thứ nhất) |
 |
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm)
1. Sau khi điều tra thời gian tự học của 40 học sinh lớp 9A, giáo viên chủ nhiệm lớp đã thu được kết quả như sau:
|
Thời gian |
[0; 1) |
[1; 2) |
[2; 3) |
[3; 4) |
|
Tần số |
10 |
15 |
8 |
7 |
\Hãy lập bảng tần số tương đối ghép nhóm của mẫu số liệu trên.
2. Giải bài toán bằng cách lập phương trình:
Hai vòi nước cùng chảy vào một bể thì sau 6 giờ đầy bể. Nếu mỗi vòi chảy một mình cho đầy bể thì vòi II cần nhiều thời gian hơn vòi I là 5 giờ. Tính thời gian mỗi vòi chảy một mình đầy bể.
Bài 2. (1,5 điểm) Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F.
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.
b) Chứng minh KH song song với ED và tam giác ACF là tam giác cân.
c) Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.
-----HẾT-----
Xem thử Đề thi CK2 Toán 9 KNTT Xem thử Đề thi CK2 Toán 9 CTST Xem thử Đề thi CK2 Toán 9 CD
Lưu trữ: Đề thi Học kì 2 Toán 9 (sách cũ)
Xem thêm đề thi Toán 9 có đáp án, chọn lọc hay khác:
Top 50 Đề thi Toán 9 Giữa kì 1 năm 2026 (cấu trúc mới, có đáp án)
Top 50 Đề thi Toán 9 Học kì 1 năm 2026 (cấu trúc mới, có đáp án)
Top 50 Đề thi Toán 9 Giữa kì 2 năm 2026 (cấu trúc mới, có đáp án)
Xem thêm đề thi lớp 9 các môn học có đáp án hay khác:
Tài liệu giáo án lớp 9 các môn học chuẩn khác:
Loạt bài Đề thi Toán lớp 9 năm 2025 học kì 1 và học kì 2 được biên soạn bám sát cấu trúc ra đề thi mới Tự luận và Trắc nghiệm giúp bạn giành được điểm cao trong các bài thi Toán lớp 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 9 (các môn học)
- Giáo án điện tử lớp 9 (các môn học)
- Giáo án Toán 9
- Giáo án Ngữ văn 9
- Giáo án Tiếng Anh 9
- Giáo án Khoa học tự nhiên 9
- Giáo án Vật Lí 9
- Giáo án Hóa học 9
- Giáo án Sinh học 9
- Giáo án Địa Lí 9
- Giáo án Lịch Sử 9
- Giáo án GDCD 9
- Giáo án Tin học 9
- Giáo án Công nghệ 9
- Đề thi lớp 9 (các môn học)
- Đề thi Ngữ Văn 9 (có đáp án)
- Đề thi Toán 9 (có đáp án)
- Đề thi Tiếng Anh 9 mới (có đáp án)
- Đề thi Tiếng Anh 9 (có đáp án)
- Đề thi Khoa học tự nhiên 9 (có đáp án)
- Đề thi Lịch Sử và Địa Lí 9 (có đáp án)
- Đề thi GDCD 9 (có đáp án)
- Đề thi Tin học 9 (có đáp án)
- Đề thi Công nghệ 9 (có đáp án)

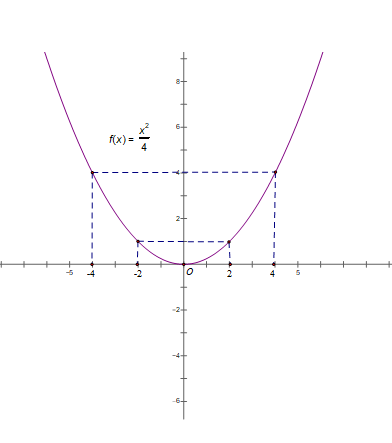
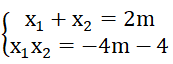
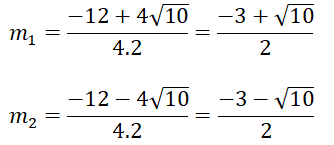
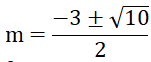 thì phương trình có 2 nghiệm x1; x2 thỏa mãn điều kiện x12 + x22 - x1 x2 = 13
thì phương trình có 2 nghiệm x1; x2 thỏa mãn điều kiện x12 + x22 - x1 x2 = 13 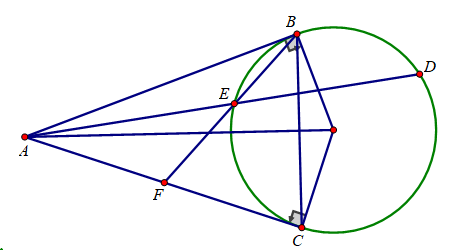


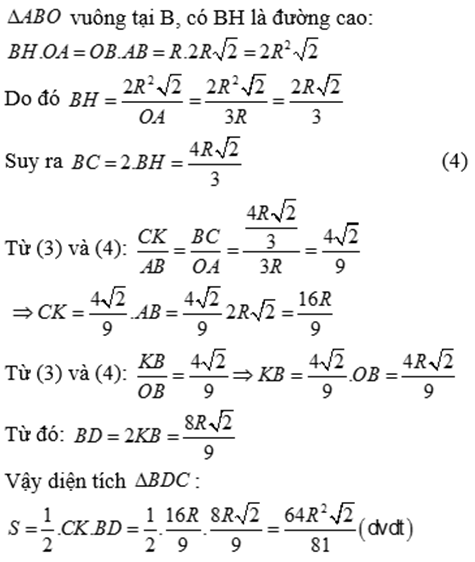
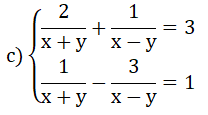
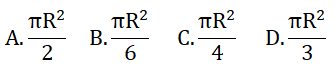
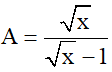
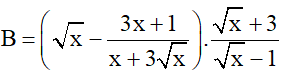 với x > 0; x ≠ 1
với x > 0; x ≠ 1 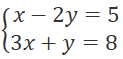 có nghiệm là:
có nghiệm là: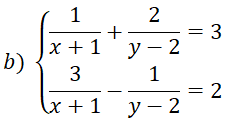

 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp



