Top 50 Đề thi Toán 9 Giữa kì 1 năm 2026 (cấu trúc mới, có đáp án)
Trọn bộ 50 đề thi Toán 9 Giữa kì 1 theo cấu trúc mới sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều có đáp án và ma trận sẽ giúp bạn ôn tập và đạt điểm cao trong bài thi Toán 9.
Top 50 Đề thi Toán 9 Giữa kì 1 năm 2026 (cấu trúc mới, có đáp án)
Xem thử Đề thi GK1 Toán 9 KNTT Xem thử Đề thi GK1 Toán 9 CTST Xem thử Đề thi GK1 Toán 9 CD
Chỉ từ 150k mua trọn bộ đề thi Toán 9 Giữa kì 1 theo cấu trúc mới bản word có lời giải chi tiết, dễ dàng chỉnh sửa:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Đề thi Toán 9 Giữa kì 1 (Giáo viên VietJack)
Đề thi Giữa kì 1 Toán 9 theo bộ sách
Đề thi Giữa kì 1 Toán 9 năm 2025-2026 (trên cả nước)
Đề thi Giữa kì 1 Toán 9 THCS&THPT Lương Thế Vinh (Hà Nội) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS Lê Quý Đôn (TP HCM) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS Nguyễn Trường Tộ (Hà Nội) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS&THPT Lê Quý Đôn (Hà Nội) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS Nghĩa Tân (Hà Nội) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS Nguyễn Thị Định (Đắk Lắk) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS Thành Công (Hà Nội) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS Đinh Ruối (Gia Lai) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 THCS An Lão (Ninh Bình) năm 2025-2026
Đề thi Giữa kì 1 Toán 9 theo Tỉnh/ Thành phố
- Đề thi Giữa kì 1 Toán 9 Hà Nội
- Đề thi Giữa kì 1 Toán 9 TP Hồ Chí Minh
- Đề thi Giữa kì 1 Toán 9 Ninh Bình
- Đề thi Giữa kì 1 Toán 9 Bắc Ninh
- Đề thi Giữa kì 1 Toán 9 Hải Phòng
- Đề thi Giữa kì 1 Toán 9 Đà Nẵng
- Đề thi Giữa kì 1 Toán 9 Tp. Huế
- Đề thi Giữa kì 1 Toán 9 Khánh Hòa
- Đề thi Giữa kì 1 Toán 9 Đồng Tháp
- Đề thi Giữa kì 1 Toán 9 Tuyên Quang
- Đề thi Giữa kì 1 Toán 9 Lạng Sơn
- Đề thi Giữa kì 1 Toán 9 Quảng Trị
- Đề thi Giữa kì 1 Toán 9 Gia Lai
- Đề thi Giữa kì 1 Toán 9 ĐắK LắK
Xem thử Đề thi GK1 Toán 9 KNTT Xem thử Đề thi GK1 Toán 9 CTST Xem thử Đề thi GK1 Toán 9 CD
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa kì 1 - Kết nối tri thức
năm 2025
Môn: Toán 9
Thời gian làm bài: phút
(Đề 1)
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn?
A. 2x - 3y = 5
B. 0x + 2y = 4
C. 2x - 0y = 3
D. 0x - 0y = 6
Câu 2. Cặp số nào dưới đây là thuộc đường thẳng biểu diễn nghiệm của phương trình 2x - 5 = 19?
A. (2; -3)
B. (1; 1)
C. (1; -2)
D. (12; -1)
Câu 3. Cho hệ phương trình Cho các khẳng định sau:
(i) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 6y = -1.
(ii) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 0x = -1.
(iii) Hệ phương trình đã cho vô nghiệm.
Số khẳng định đúng trong các khẳng định trên là
A. 0.
B. 1.
C. 2.
D. 3.
Câu 4. Hình nào dưới đây biểu diễn tất cả các nghiệm của phương trình 2x - 3y = 5?
Câu 5. Điều kiện xác định của phương trình là
A.
B.
C. và
D. và
Câu 6. Tổng các nghiệm của phương trình là
A. 5
B. 1
C. -5
D. -1
Câu 7. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. x + y > 8
B. 0x + 5 ≥ 0
C. 2x - 3 > 4
D. x2 - 6x + 1 ≤ 0
|
Câu 8. Biển báo giao thông trong hình bên báo đường cấm các xe cơ giới và thô sơ (kể cả các xe được ưu tiên theo quy định) có độ dài toàn bộ kể cả xe và hàng lớn hơn trị số ghi trên biển đi qua. Nếu xe có chiều rộng lớn hơn 3,2 mthì không được phép lưu thông để đảm bảo an toàn cho cả xe và các phương tiện khác, cũng như tránh gây cản trở giao thông. Nếu một xe tải đi trên đường đó có chiều rộng a (m) thỏa mãn điều kiện nào sau đây là đúng nhất? |
|
A. a ≤ 3,2.
B. a > 3,2
C. a ≥ 3,2.
D. a = 3,2.
Câu 9. Cho tam giác MNP vuông tại M có đường cao MH và . Tỉ số bằng
A. cot α.
B. cos α.
C. sin α.
D. tan α.
Câu 10. Cho tam giác ABC vuông tại A. Hệ thức nào sau đây không đúng?
A.
B.
C.
D.
Câu 11. Cho góc α thỏa mãn . Biết . Giá trị của bằng
A.
B.
C.
D.
Câu 12. Cho hình bình hành ABCD có và . Hỏi diện tích của hình bình hành là bao nhiêu? (Kết quả làm tròn đến hàng phần mười)
A. 14
B. 14,6
C. 14,5
D. 14,9
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Cho phương trình 4x - 7y = -1 (*).
a) Hệ số a, b, c của phương trình (*) lần lượt là 4; -7; -1.
b) Phương trình (*) là không phải phương trình bậc nhất hai ẩn vì hệ số b < 0.
c) Cặp số (0; 5) là nghiệm của phương trình (*).
d) Biểu diễn hình học tất cả các nghiệm của phương trình (*) là đường thẳng
d) Tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình (*) là đường thẳng y = 2x - 1.
Câu 14. Cho hai số a, b và a > 1 > b.
a) a - 1 > 0.
b) a - b < 0.
c) (a - 1)(b - 1) < 0.
d) a - 2b < - 1
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Cho hệ phương trình có nghiệm (x; y). Tính tổng x + y.
Câu 16. Phương trình có bao nhiêu nghiệm?
Câu 17. Tìm giá trị nguyên lớn nhất của x thỏa mãn bất phương trình .
Câu 18. Biết tính giá trị biểu thức
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Anh Hoài đã đến phòng tập thể dục và tập 40 phút Yoga, sau đó nhảy Jumping jacks 10 phút và tiêu hao được 510 calo. Lần tiếp theo anh Hoài tập 30 phút Yoga và thực hiện nhảy Jumping jacks 20 phút, lượng calo tiêu hao được là 470 calo. Hỏi có bao nhiêu calo đã tiêu hao trong mỗi phút tập Yoga? Có bao nhiêu calo đã tiêu hao trong mỗi phút tập Jumping jacks?
Bài 2. (1,5 điểm)
1) Cho tam giác ABC có đường cao Tính độ dài các cạnh của tam giác ABC (làm tròn kết quả đến chữ số thập phân thứ hai).
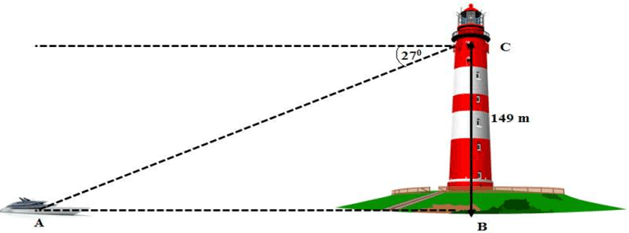
2) Một người quan sát ở đài hải đăng cao 149 m so với mực nước biển nhìn thấy một con tàu ở xa với một góc nghiêng xuống đất là 27°. Hỏi tàu đang đứng cách chân hải đăng là bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị)
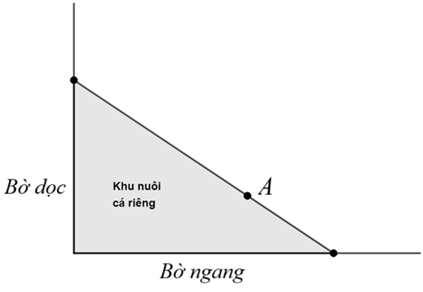
Bài 3. (0,5 điểm) Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
-----HẾT-----
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa kì 1 - Kết nối tri thức
năm 2025
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Cặp số nào sau đây không phải là nghiệm của phương trình 2x – y – 1 = 0?
A. (1; 1).
B. (2; 3).
C. (1; –2).
D. (0; –1).
Câu 2. Hệ phương trình có nhiều nhất bao nhiêu nghiệm?
A. 0.
B. 1.
C. 2.
D. Vô số.
Câu 3. Cho tam giác ABC vuông tại A có đường cao AH. Khi đó bằng
A. sinC.
B. cosC.
C. tanC.
D. cotC.
Câu 4. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90° và sinα = 0,5. Khẳng định nào sau đây là đúng?
A. sinβ = 0,5.
B. cosβ = 0,5.
C. tanβ = 0,5.
D. cotβ = 0,5.
Phần 2. Câu trắc nghiệm đúng sai
Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 5. Cho ba số a, b, c thỏa mãn a > b và c < 0.
a) ac < bc.
b) .
c) 2a – c > 2b – c.
d) c – 3a > c – 3b.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 6. Xác định hàm số y = ax + b để đồ thị của nó đi qua hai điểm A(–2; –1) và B(1; 4).
Câu 7. Cho tam giác ABC vuông tại A có AB = 5 cm và AC = 11 cm. Số đo góc B được làm tròn đến phút là bao nhiêu?
B. TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm) Giải các phương trình và bất phương trình sau:
a) (2x + 5)(1 – 4x) = 0.
b) .
c) 13 – 5x > –3x + 9.
d) .
Bài 2. (2,5 điểm)
a) Tìm các hệ số x và y trong phản ứng hóa học đã được cân bằng sau:
xFe3O4 + O2 → yFe2O3.
Từ đó, hãy hoàn thiện phương trình phản ứng hóa học sau khi được cân bằng.
b) Giải bài toán sau bằng cách lập hệ phương trình:
Khi cho hai vòi nước cùng chảy vào một bể cạn thì sau 1 giờ 20 phút sẽ đầy bể. Nếu mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì sẽ được bể. Hỏi nếu chảy riêng, mỗi vòi nước sẽ chảy đầy bể trong bao lâu?
Bài 3. (2,5 điểm)
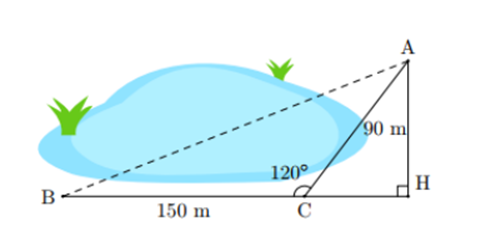
1) Bạn An muốn tính khoảng cách AB (làm tròn đến hàng phần mười của mét) ở hai bên hồ nước (hình vẽ). Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và bạn ấy dùng giác kế đo được . Hãy tính AB giúp bạn An.
2) Cho tam giác ABC vuông tại A có đường cao AH (H ∈ BC).
a) Biết AC = 4 cm và . Tính độ dài đường cao AH, cạnh AB và BC (làm tròn kết quả đến hàng phần trăm của cm).
b) Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N. Chứng minh rằng .
-----HẾT-----
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa kì 1 - Chân trời sáng tạo
năm 2025
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (4,0 điểm)
Phần 1. Câu trắc nghiệm đúng sai
Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 1. Cho phương trình 2x - 5y = 1 (*)
|
|
Đúng |
Sai |
|
a) Cặp số (-2;1) là nghiệm của phương trình (*). |
|
|
|
b) Phương trình (*) là phương trình bậc nhất hai ẩn có vô số nghiệm. |
|
|
|
c) Hệ số a; b; c của phương trình (*) lần lượt là 2; 5; 1. |
|
|
|
d) Tập hợp các điểm có tọa độ (x;y) thỏa mãn phương trình (*) là một đường thẳng |
|
|
Phần 2. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 2 đến câu 7, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 2. Điều kiện xác định của phương trình là
A. x ≠ 2.
B. x ≠ -1.
C. x ≠ 2 và x ≠ -1.
D. x ≠ 2 và x ≠ 0.
Câu 3. Cặp số nào sau đây là nghiệm của hệ phương trình ?
A. (1;1).
B. (-21;15).
C. (1;-1).
D. (21;-15).
Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. x + y > 8.
B. 0x + 5 ≥ 0.
C. 2x - 3 > 4.
D. x2 - 6x + 1 ≤ 0.
|
Câu 5. Biển báo giao thông trong hình bên báo đường cấm các xe cơ giới và thô sơ (kể cả các xe được ưu tiên theo quy định) có độ dài toàn bộ kể cả xe và hàng lớn hơn trị số ghi trên biển đi qua. Nếu xe có chiều rộng lớn hơn 3,2m thì không được phép lưu thông để đảm bảo an toàn cho cả xe và các phương tiện khác, cũng như tránh gây cản trở giao thông. Nếu một xe tải đi trên đường đó có chiều rộng a (m) thỏa mãn điều kiện gì? |
|
A. a = 3,2.
B. a > 3,2.
C. a > 3,2.
D. a ≤ 3,2.
Câu 6. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90° và α = 0,5. Khẳng định nào sau đây là đúng?
A. cos β = 0,5.
B. sin β = 0,5.
C. tan β = 0,5.
D. cot β = 0,5.
Câu 7. Cho tam giác ABC vuông tại A. Hệ thức nào sau đây là sai?
A. BC = .
B. BC = .
C. BC = .
D. BC = .
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Trong mỗi câu 8 và câu 10, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 8. Nghiệm lớn nhất của phương trình (4 - 2x)(x + 1) là bao nhiêu?
Câu 9. Số nguyên nhỏ nhất thỏa mãn bất phương trình x(5x + 1) + 4(x + 3) ≥ 5x2 là bao nhiêu?
Câu 10. Biết 0° < α < 90° tính giá trị biểu thức A = .
B. TỰ LUẬN (6,0 điểm)
Bài 1. (2,0 điểm) Giải các phương trình và bất phương trình sau:
a) ;
b) .
Bài 2. (2,5 điểm)
1. Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại 180 ml nặng trung bình 10kg. Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 5,25 tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng 65 kg?
2. Giải bài toán sau bằng cách lập hệ phương trình:
Do ảnh hưởng của dịch Covid – 19 nên trong tháng hai cả hai tổ công nhân chỉ làm được 700 sản phẩm. Sang tháng ba, tình hình dịch ổn định tổ I vượt mức 20% tổ II vượt mức 15% nên cả hai tổ làm được 830 sản phẩm. Hỏi trong tháng hai mỗi tổ làm được bao nhiêu sản phẩm?
Bài 3. (2,0 điểm) Lúc 6 giờ sáng, bạn An đi từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc đỉnh C được mô tả như hình vẽ dưới. Cho biết đoạn AB dài 762 m, .
a) Tính chiều cao con dốc (làm tròn kết quả đến hàng đơn vị của mét).
b) Hỏi bạn An đến trường lúc mấy giờ (làm tròn kết quả đến phút)? Biết rằng tốc độ lên dốc là 4 km/h và tốc độ xuống dốc là 19 km/h.
Bài 4. (0,5 điểm) Cho x, y là hai số thực thỏa mãn điều kiện x2 + 2y2 + 2xy + 7x + 7y + 10 = 0.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = .
-----HẾT-----
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa kì 1 - Cánh diều
năm 2025
Môn: Toán 9
Thời gian làm bài: phút
A. TRẮC NGHIỆM (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 4, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Mẫu thức chung khi quy đồng mẫu thức của phương trình là
A. (x – 1)2.
B. (x + 1)2.
C. (x – 1)(x + 1).
D. x(x – 1)(x + 1).
Câu 2. Cho hệ phương trình . Cho các khẳng định sau:
(i) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 6y = –1.
(ii) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: 0x = –1.
(iii) Hệ phương trình đã cho vô nghiệm.
Số khẳng định đúng trong các khẳng định trên là
A. 0.
B. 1.
C. 2.
D. 3.
Câu 3. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Khẳng định nào sau đây là đúng?
A. .
B. .
C. b = c.cosC.
D. c = b.tanC.
Câu 4. Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là đúng?
A. AB2 = BC2 + AC2.
B. sinC = cosB.
C. cotB – tanB = 0.
D. .
Phần 2. Câu trắc nghiệm đúng sai
Trong câu 5, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 5. Cho bất đẳng thức –5a > 3.
a) Số a có giá trị là một số âm.
b) Biểu thức 3 – 5a có giá trị là một số dương.
c) Biểu thức có giá trị là một số dương.
d) Biểu thức –10a – 10 có giá trị là một số âm.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Trong mỗi câu 6 và câu 7, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 6. Tìm nghiệm của hệ phương trình .
Câu 7. Cho tam giác ABC vuông tại A có AB = 5 cm và đường cao AH = 3 cm. Tính số đo góc C (làm tròn kết quả đến phút).
B. TỰ LUẬN (7,0 điểm)
Bài 1. (2,5 điểm)
1. Giải các phương trình sau:
a) 4x(x + 3) – 3x – 9 = 0.
b) .
2. Giải các bất phương trình sau:
a) 3x – 8 < 4x – 12.
b) 3(x – 2) – 5 > 3(2x – 1).
c) .
Bài 2. (2,0 điểm)
1. Xác định a và b sao cho hệ phương trình nhận cặp số (–3; 2) làm nghiệm.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một ôtô dự định đi từ A đến B trong khoảng thời gian nhất định. Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi chậm mất so với dự định là 5 giờ. Tính vận tốc và thời gian dự định của ôtô.
Bài 3. (2,0 điểm)
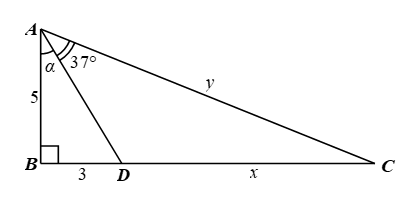
1. Cho hình vẽ bên. Tính số đo góc α và các độ dài x, y (góc làm tròn đến độ và độ dài làm tròn đến hàng phần trăm).
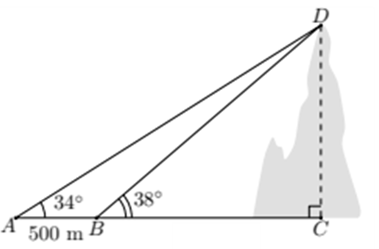
2. Tính chiều cao của một ngọn núi (kết quả làm tròn đến hàng đơn vị), biết tại hai điểm A, B cách nhau 500 m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34° và 38° (hình vẽ).
Bài 4. (0,5 điểm) Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo, chứng minh rằng:
-----HẾT-----
Xem thử Đề thi GK1 Toán 9 KNTT Xem thử Đề thi GK1 Toán 9 CTST Xem thử Đề thi GK1 Toán 9 CD
Lưu trữ: Đề thi Giữa kì 1 Toán 9 (sách cũ)
Xem thêm đề thi Toán 9 có đáp án, chọn lọc hay khác:
Xem thêm đề thi lớp 9 các môn học có đáp án hay khác:
Tài liệu giáo án lớp 9 các môn học chuẩn khác:
Loạt bài Đề thi Toán lớp 9 năm 2025 học kì 1 và học kì 2 được biên soạn bám sát cấu trúc ra đề thi mới Tự luận và Trắc nghiệm giúp bạn giành được điểm cao trong các bài thi Toán lớp 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 9 (các môn học)
- Giáo án điện tử lớp 9 (các môn học)
- Giáo án Toán 9
- Giáo án Ngữ văn 9
- Giáo án Tiếng Anh 9
- Giáo án Khoa học tự nhiên 9
- Giáo án Vật Lí 9
- Giáo án Hóa học 9
- Giáo án Sinh học 9
- Giáo án Địa Lí 9
- Giáo án Lịch Sử 9
- Giáo án GDCD 9
- Giáo án Tin học 9
- Giáo án Công nghệ 9
- Đề thi lớp 9 (các môn học)
- Đề thi Ngữ Văn 9 (có đáp án)
- Đề thi Toán 9 (có đáp án)
- Đề thi Tiếng Anh 9 mới (có đáp án)
- Đề thi Tiếng Anh 9 (có đáp án)
- Đề thi Khoa học tự nhiên 9 (có đáp án)
- Đề thi Lịch Sử và Địa Lí 9 (có đáp án)
- Đề thi GDCD 9 (có đáp án)
- Đề thi Tin học 9 (có đáp án)
- Đề thi Công nghệ 9 (có đáp án)

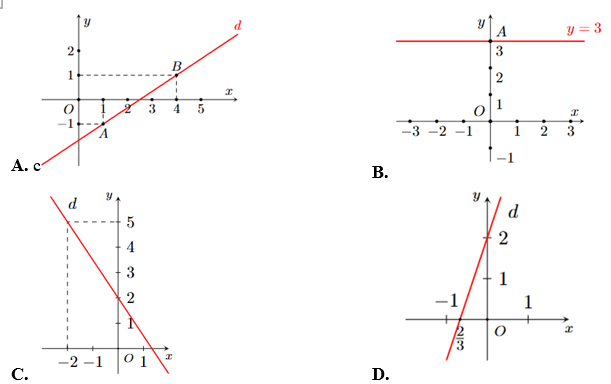














 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp



