Đề thi Giữa học kì 1 Toán 9 Hà Nội năm 2025 (7 đề)

Tuyển chọn Đề thi Giữa học kì 1 Toán 9 Hà Nội năm 2025 (7 đề) chọn lọc được các Giáo viên nhiều năm kinh nghiệm biên soạn và sưu tầm từ đề thi Toán 9 của các trường THCS. Hi vọng bộ đề thi này sẽ giúp học sinh ôn tập và đạt kết quả cao trong các bài thi Giữa Học kì 1 môn Toán 9.

Đề thi Giữa học kì 1 Toán 9 Hà Nội năm 2025 (7 đề)

Xem thử

Chỉ từ 150k mua trọn bộ trên Đề thi Giữa kì 1 Toán 9 theo cấu trúc mới bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Hà Nội

năm 2025

Bài thi môn: Toán 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 1)

Câu 1. (2 điểm) Rút gọn biểu thức sau:

 

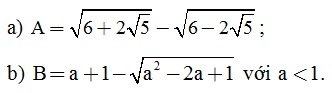
Câu 2. (2 điểm) Cho biểu thức:

 

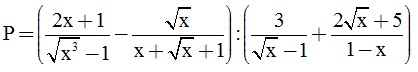
a) Rút gọn biểu thức P.

b) Tính giá trị của P khi  .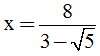

c) Tìm x để P có giá trị là số tự nhiên.

Câu 3. (2 điểm) Giải phương trình:

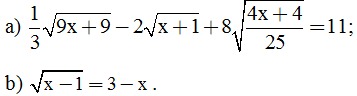
Câu 4. (3,5 điểm) 

1) Một chiếc đò đang ở điểm A muốn băng qua sông theo đường AH vuông góc với bờ bên kia nhưng bị nước cuốn đi nên tấp vào bờ bên kia ở điểm B cách H 50m (BH = 50m). Tìm chiều rộng con sông (AH) và quãng đường đò đã đi (AB). 

2) Cho ΔABC có AC = 16cm, AB = 12cm, BC = 20cm. Đường cao AH.  

a) Chứng minh ΔABC vuông.                    

b) Tính AH, ∠B, ∠C  .      

c) Từ H kẻ HE, HF lần lượt vuông góc với AC, AB. Tính HE, HF.  

d) So sánh:  tanB và sinB  (không dùng bảng và máy tính bỏ túi).

Câu 5. (0,5 điểm) Giải phương trình:  .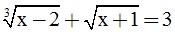

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Hà Nội

năm 2025

Bài thi môn: Toán 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 2)

Câu 1. (2 điểm) Cho biểu thức:

   .

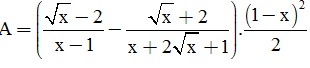a) Rút gọn A nếu x ≥ 0, x ≠ 1 .

b) Tìm x để A dương.

c) Tìm giá trị lớn nhất của A.  

Câu 2. (3 điểm) Thực hiện các phép tính sau:

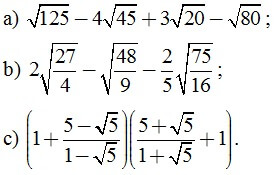
Câu 3. (1 điểm) Cho 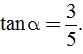Hãy tính giá trị của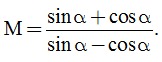  

Câu 4. (3,5 điểm) 

1) Một cái thang dài 3,5 m đặt dựa vào tường, góc “an toàn” giữa thang và mặt đất để thang không bị đổ khi người trèo lên là 65⁰. Tính khoảng cách từ chân thang đến bức tường. (Kết quả làm tròn đến chữ số thập phân thứ nhất).

2) Cho tam giác ABC vuông tại A, ∠C = 30^o, BC = 10cm    .

a) Tính AB, AC.        

b) Từ A kẻ AM, AN lần lượt vuông góc với các đường phân giác trong, ngoài của góc B. Chứng minh rằng: MN || BC và MN = AB. 

c) Chứng minh rằng: ΔMAB ∼ ΔABC .

Câu 5. (0,5 điểm) Với các số thực x, y thỏa mãn x + y ≤ 1 

Tìm giá trị nhỏ nhất của biểu thức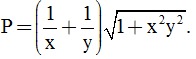  

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Hà Nội

năm 2025

Bài thi môn: Toán 9

Thời gian làm bài:60 phút

(không kể thời gian phát đề)

(Đề số 3)

Câu 1. (1,0 điểm) Tìm điều kiện của x để các căn thức sau có nghĩa:

 

Câu 2. (2,0 điểm) Tính: 

 

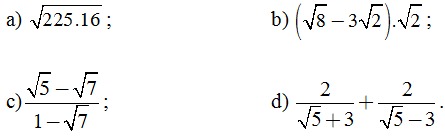
Câu 3. (1,0 điểm) Cho biểu thức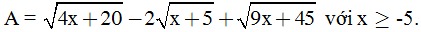  

a) Rút gọn A.

b) Tìm x để A = 6

Câu 4. (2,0 điểm) Cho biểu thức:

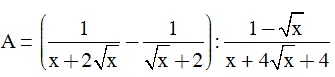(với x > 0; x ≠ 1)

a)  Rút gọn biểu thức A. 

b)  Tìm x để  .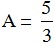

Câu 5. (3,5 điểm) Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.

a) Tính độ dài các đoạn thẳng AB, AC, AH.

b) Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.

c) Chứng minh rằng: S_BHD =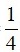 S_{BKC .} cos²∠ABD. 

Câu 6.(1,0 điểm) Giải phương trình sau.

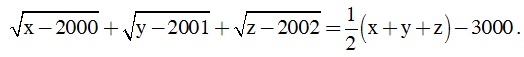
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Hà Nội

năm 2025

Bài thi môn: Toán 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 4)

Câu 1. (2,0 điểm)

1. Thực hiện phép tính.

 

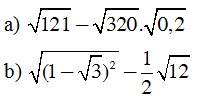
2. Tìm điều kiện của x để các biểu thức sau có nghĩa: 

 a) 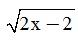; b)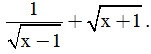  

Câu 2. (2,0 điểm)

1. Phân tích đa thức thành nhân tử.

a) ab + b√a + √a + 1 (với a ≥ 0)

b) 4a + 1 (với a < 0)

2. Giải phương trình: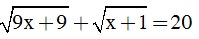  

Câu 3. (2,0 điểm) Cho biểu thức M = 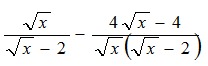 với x > 0 , x ≠ 4.

a) Rút gọn biểu thức M;

b) Tính giá trị của M khi x = 3 + 2√2  ;

c) Tìm giá trị của x để M > 0.

Câu 4. (3,0 điểm) Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn : BH = 4 cm và HC = 6 cm. 

a) Tính độ dài các đoạn AH, AB, AC.

b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn đến độ).

c) Kẻ AK vuông góc với BM (K thuộc BM). Chứng minh : BK.BM = BH.BC.

Câu 5. (0,5 điểm) Cho biểu thức P = x³ + y³ - 3(x + y) + 1993. Tính giá trị biểu thức P với: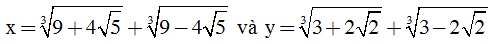  

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Hà Nội

năm 2025

Bài thi môn: Toán 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 5)

Câu 1. (2 điểm) Thực hiện phép tính:

 

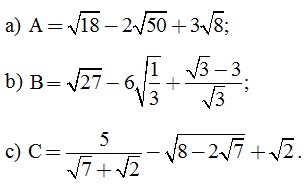
Câu 2. (2 điểm) Tìm x, biết:

 

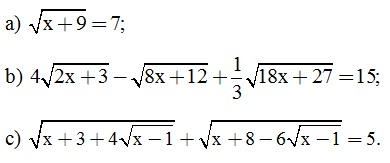
Câu 3. (2 điểm) Cho hai biểu thức 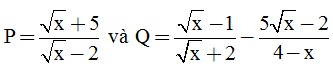 với x ≥ 0, x ≠ 4

a) Tính giá trị biểu thức P khi x = 9.

b) Rút gọn biểu thức Q.

c) Đặt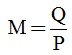 . Tìm x để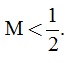  

d) Tìm các giá trị nguyên của x để M có giá trị nguyên.

Câu 4. (3,5 điểm) Cho tam giác ABC vuông tại A, vẽ đường cao AH của . 

a) Nếu sin∠ABC = 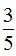  và BC = 20cm. Tính các cạnh AB, AC, BH và góc ∠ACB  (số đo góc làm tròn đến độ).

b) Đường thẳng vuông góc với BC tại B, cắt đường thẳng AC tại D. Chứng minh rằng: AD.AC = BH.BC.

c) Kẻ tia phân giác BE của ∠DBA (E thuộc đoạn DA). Chứng minh rằng: tan ∠EBA =    .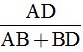

d) Lấy điểm K thuộc đoạn AC, kẻ KM vuông góc với HC tại M, KN vuông góc với AH tại N. Chứng minh rằng: HN.NA + HM.MC = KA.KC.

Câu 5. (0,5 điểm) Cho x, y thay đổi thỏa mãn 0 < x < 1, 0 < y < 1.

Tìm giá trị lớn nhất của biểu thức: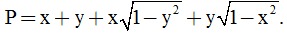 

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Hà Nội

năm 2025

Bài thi môn: Toán 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 6)

Câu 1. (2 điểm) Rút gọn biểu thức:

 

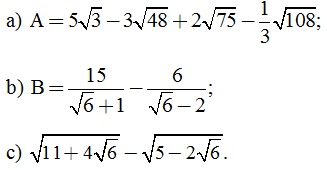
Câu 2. (2 điểm) Giải phương trình: 

 

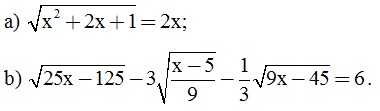
Câu 3. ( 2 điểm) Cho biểu thức:

  

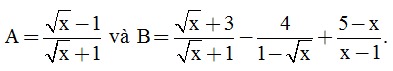
a) Tìm điều kiện của x để A và B đều có nghĩa.

b) Tính giá trị của A khi x = 9.

c) Rút gọn biểu thức P = A.B.

Câu 4. (3,5 điểm) Cho tam giác ABC vuông tại A có ∠B = 60^o  , BC = 6cm.

a) Tính AB, AC (độ dài làm tròn đến 1 chữ số thập phân).

b) Vẽ đường cao AH của tam giác ABC. Tính HB, HC.

c) Trên tia đối của tia BA lấy điểm D sao cho DB = BC. Chứng minh rằng: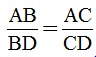 

d) Từ A kẻ đường thẳng song song với phân giác của ∠CBD cắt CD tại K. Chứng minh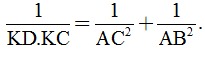  

Câu 5. (0,5 điểm) Giải phương trình

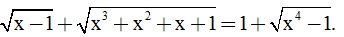
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa Học kì 1 Hà Nội

năm 2025

Bài thi môn: Toán 9

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 7)

Câu 1. (2 điểm) Thực hiện phép tính và rút gọn các biểu thức sau:

 

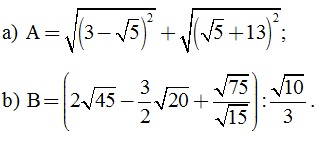
Câu 2. (2 điểm) Giác các phương trình sau:

a)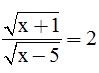 ; b)  .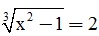

Câu 3. (2 điểm) Cho biểu thức

 

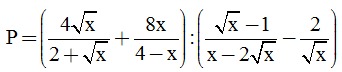
với x > 0, x ≠ 4, x ≠ 9  

a) Rút gọn P.

b) Tính giá trị của P khi x = 25.

c) Với x > 9, tìm giá trị nhỏ nhất của P.

Câu 4. (3,5 điểm) Cho tam giác ABC vuông tại A có đường cao AH. Gọi E và F lần lượt là hình chiếu vuông góc của H lên AB, AC.

a) Cho biết AB = 3cm, ∠ACB = 30^o . Tính độ dài các đoạn AC, HA.

b) Chứng minh: BE.BA + CF.CA + 2HB.HC = BC².

c) Biết BC = 6cm. Tính giá trị lớn nhất của diện tích tứ giác HEAF.

Câu 5. (0,5 điểm) Giải phương trình:

 

................................

................................

................................

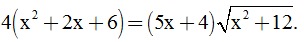
Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 9 năm 2025 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---