Đề thi Giữa kì 2 Toán 9 có đáp án (6 đề)

Với Đề thi Giữa kì 2 Toán 9 có đáp án (6 đề), chọn lọc giúp học sinh ôn tập và đạt kết quả cao trong bài thi Giữa kì 2 Toán 9.

Đề thi Giữa kì 2 Toán 9 có đáp án (6 đề)

Xem thử

Chỉ từ 150k mua trọn bộ trên 80 Đề thi Giữa kì 2 Toán 9 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 1)

I. Trắc nghiệm (1 điểm)

Câu 1: Hệ phương trình   (với a; b; c; a’; b’; c’ khác 0)

Khi nào hệ có nghiệm duy nhất

A)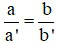  

B)  

C)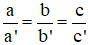  

D)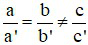  

Câu 2: Một nghiệm của phương trình x + 3y = 5 là

A) (1; 2)

B) (2; 3)

C) (2; 1)

D) (4; 1)

Câu 3: Khẳng định nào sau đây đúng

A) Góc ở tâm có số đo bằng 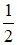  số đo cung bị chắn

B) Góc nội tiếp có số đo bằng với số đo cung bị chắn

C) Góc có đỉnh nằm bên ngoài đường tròn có số đo bằng 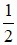  tổng số đo hai cung bị chắn.

D) Góc tạo bởi tiếp tuyến và dây cung có số đo bằng 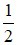  số đo cung bị chắn

Câu 4: Gọi l là độ dài cung ; bán kính đường tròn là R; số đo cung là n (độ). Đọ dài cung là:

A)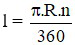  

B)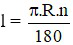  

C)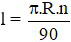  

D)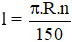  

II. Tự luận

Bài 1 (1,5 điểm): Cho hệ phương trình: 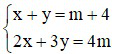   (m là tham số)

a) Giải hệ phương trình khi m = 1

b) Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m.

Bài 2 (1,5 điểm): Cho hàm số y = 0,2x² và y = x.

a) Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ giao điểm của hai đồ thị.

Bài 3 (2 điểm): Một ô tô dự định đi từ A đến B trong một khoảng thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến sớm hơn dự định 3h. Nếu mỗi giờ xe chạy chậm hơn dự định 10km thì đến nơi chậm mất 5h. Tính vận tốc xe lúc đầu và thời gian dự định đi trên quãng đường AB.

Bài 4 (3,5 điểm): Cho đường tròn (O; R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).

a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC

b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.

c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.

d) Tính theo R diện tích tam giác BDC.

Bài 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức: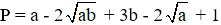  

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 2)

Bài 1 (2 điểm): Cho biểu thức: 

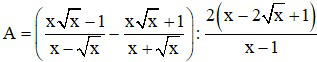
Điều kiên x > 0 và x ≠ 1

a) Rút gọn A.

b) Tìm x để A < 0

Bài 2 (2 điểm): Cho hệ phương trình với m là tham số 

   (*)

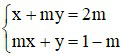a) Tìm m để hệ phương trình đã cho có nghiệm duy nhất. Tìm nghiệm duy nhất đó.

b) Tìm m để hệ phương trình đã cho vô nghiệm.

Bài 3 (2 điểm): Hai bạn An và Khoa cùng làm chung một công việc sau 6 giờ thì xong. Biết nếu làm một mình xong công việc thì Khoa làm lâu hơn An 9 giờ. Tính thời gian làm một mình xong công việc của An, Khoa.

Bài 4 (3,5 điểm): Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I  (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC ( E khác B và C), AE cắt CD tại F. Chứng minh: 

a) BEFI là tứ giác nội tiếp đường tròn.

b) AE.AF = AC².

c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.

Bài 5 (0,5 điểm): Cho hai số dương a, b thỏa mãn: a + b ≤ 2√2 . Tìm giá trị nhỏ nhất của biểu thức:  .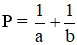

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 3)

Bài 1 (2 điểm): Giải các phương trình và hệ phương trình sau:

a) x² – 5x + 6 = 0

b)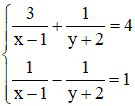  

Bài 2 (2 điểm): Hai vòi nước cùng chảy vào bể thì sau 4 giờ 48 phút đầy bể. Nếu vòi thứ nhất chảy trong 4 giờ vòi hai chảy trong 3 giờ thì được 75% bể. Tính thời gian mỗi vòi chảy một mình đầy bể.

Bài 3 (2 điểm): Cho hàm số y = ax².

a) Xác định hệ số a biết rằng đồ thị của nó cắt đường thẳng y = –2x + 3 tại điểm A có hoành độ bằng 1.

b) Vẽ đồ thị của hàm số y = –2x + 3 và của hàm số y = ax² với giá trị của a vừa tìm được trong câu a) trên cùng một mặt phẳng tọa độ.

Bài 4 (3, 5 điểm): Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh AC (M khác A và C ). Đường tròn đường kính MC cắt BC tại N và cắt tia BM tại I. Chứng minh rằng :

a) ABNM và ABCI là các tứ giác nội tiếp đường tròn.

b) NM là tia phân giác của góc  .

c) BM.BI + CM.CA = AB² + AC².

Bài 5 (0,5 điểm): Cho các số a, b, c ∈ [0; 1]. Chứng minh rằng:   a + b² + c³ – ab – bc – ca ≤ 1.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 4)

I. Trắc nghiệm (1 điểm)

Câu 1: Hệ phương trình 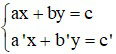  (với a; b; c; a’; b’; c’ khác 0)

Khi nào hệ vô nghiệm

A)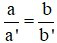  

B)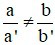  

C)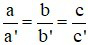  

D)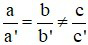

Câu 2: Một nghiệm của phương trình 2x + 3y = 1 là

A) (–1; 2)

B) (2; –3)

C) (2; –1)

D) (4; 1)

Câu 3: Khẳng định nào sau đây sai

A) Góc ở tâm có số đo bằng số đo cung bị chắn

B) Góc nội tiếp có số đo bằng với số đo cung bị chắn

C) Góc có đỉnh nằm bên ngoài đường tròn có số đo bằng 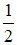  hiệu số đo hai cung bị chắn.

D) Góc tạo bởi tiếp tuyến và dây cung có số đo bằng 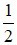  số đo cung bị chắn

Câu 4: Gọi l là độ dài cung α; bán kính đường tròn là R; số đo cung α là n (độ). Đọ dài cung α là:

A)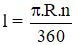  

B)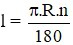  

C)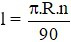  

D)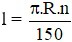

II. Tự luận

Bài 1 (2 điểm): Cho biểu thức: 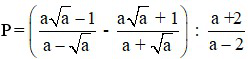  với  a > 0, a ≠ 1, a ≠ 2.

a) Rút gọn P.

b) Tìm giá trị nguyên của a để P có giá trị nguyên

Bài 2 (2 điểm): 

a) Tìm tọa độ giao điểm của đường thẳng   d:  y = –x + 2 và Parabol  (P): y = x².

b) Cho hệ phương trình:  .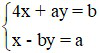

Tìm a và b để hệ đã cho có nghiệm duy nhất (x; y) = (2; –1).

Bài 3 (2 điểm): Một khu vườn hình chữ nhật có chu vi bằng 60m. Nếu tăng chiều dài lên 4 lần và chiều rộng lên 3 lần thì chu vi khu vườn sẽ tăng 162m. Tìm diện tích khi vườn.

Bài 4 (3,5 điểm): Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = 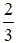  AO. Kẻ dây MN vuông góc với AB tại I, gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E.

a) Chứng minh tứ giác IECB nội tiếp .

b) Chứng minh  hệ thức: AM² = AE.AC.

c)  Hãy xác định vị trí của điểm C sao cho khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất.

Bài 5 (0,5 điểm): Cho x và y  là hai số thỏa mãn đồng thời : x ≥ 0, y ≥ 0, 2x + 3y ≤ 6 và 2x + y ≤ 4.

Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức K = x² – 2x – y.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 5)

Bài 1 (2 điểm): Cho biểu thức 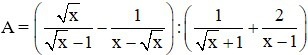 với x > 0, x ≠ 1

a) Rút gọn biểu thức A.

 b) Tính giá trị của A khi x = 2√2 + 3.

Bài 2 (2 điểm): Cho hai hàm số: y = x² và y = x + 2

a) Vẽ đồ thị của hai hàm số này trên cùng một hệ trục Oxy.

b) Tìm toạ độ các giao điểm M, N của hai đồ thị trên bằng phép tính.

Bài 3 (2 điểm): Một công ty dự định sản xuất một 1000 hộp khẩu trang so với quy định. Tuy nhiên do dịch bệnh Covid – 19 bùng phát nên công ty đã đẩy nhanh tiến độ mỗi ngày 10 hộp khẩu trang để kịp phục vụ thị trường do vậy công ty đã hoàn thành sớm hơn kế hoạch 5 ngày. Hỏi theo kế hoạch ban đầu công ty dự kiến sản xuất trong bao nhiêu ngày.

Bài 4 (3, 5 điểm): Cho đường tròn (O; R) và điểm A nằm ngoài (O) sao cho OA = 3R. Vẽ các tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Vẽ cát tuyến AMN với (O) (M nằm giữa A và N và AMN không đi qua O). Gọi I là trung điểm của MN.

a) Chứng minh 5 điểm A, B, O, I, C thuộc một đường tròn

b) Chứng minh AM.AN = 8R²

c) Tính độ dài AM, AN khi MN = R√3

Bài 5 (0, 5 điểm): Cho ba số a, b, c > 0. Chứng minh rằng:

 

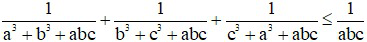
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 6)

Bài 1 (2 điểm): Cho biểu các biểu thức:

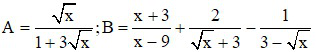  với x > 0; x 9.

a) Tính A khi x =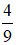  

b) Rút gọn B

c) Cho P = B: A. Tìm x để P < 3

Bài 2 (2 điểm): Cho hệ phương trình với m là tham số

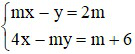  (I)

 Tìm điều kiện của m để hệ phương trình có nghiệm.

Bài 3 (2 điểm): Hai xí nghiệp tổng cộng phải làm 360 dụng cụ. Trên thực tế xí nghiệp I vượt mức 12%, xí nghiệp II vượt mức 10% nên tổng dụng cụ làm được là 400 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm so với dự định.

Bài 4 (3, 5 điểm): Trên đường tròn (O) đường kính AB, lấy điểm D (D khác A; D khác B). Gọi E là điểm chính giữa cung nhỏ BD. Lấy điểm C trên đoạn thẳng AB (C khác A và C khác B). Đường thẳng CE cắt đường tròn (O) tại điểm thứ hai là F. GỌi G là giao điểm của AE và DF.

a) Chứng minh: 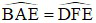  và AGCF là tứ giác nội tiếp.

b) Chứng minh CG vuông góc với AD.

c) Kẻ đường thẳng đi qua C, song song với AD và cắt DF tại H. Chứng minh CH = CB.

Bài 5 (0,5 điểm): Cho x, y, z là các số thực thỏa mãn: x + y + x = 1

Tìm giá trị nhỏ nhất của biểu thức: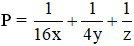  

................................

................................

................................

Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 9 năm 2024 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---