Bộ 10 Đề thi Toán 9 Giữa kì 2 năm 2024 tải nhiều nhất

Với Bộ 10 Đề thi Toán 9 Giữa kì 2 năm 2024 tải nhiều nhất, chọn lọc giúp học sinh ôn tập và đạt kết quả cao trong bài thi Giữa kì 2 Toán 9.

Bộ 10 Đề thi Toán 9 Giữa kì 2 năm 2024 tải nhiều nhất

Xem thử

Chỉ từ 150k mua trọn bộ trên 80 Đề thi Giữa kì 2 Toán 9 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 1)

I. Trắc nghiệm 

Câu 1: Tứ giác ABCD nội tiếp được trong một đường tròn. Nếu thì số đo 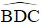  là:

A) 110^o

B) 70^o

C) 160^o

D) 140^o

Câu 2: Cho phương trình 3x + y = 5. Đâu là một nghiệm của phương trình

A) (2; 3)

B) (1; 2)

C) (-2; 4)

D) (3; 6)

Câu 3: Cho phương trình 2x – y – 5. Phương trình nào sau đây kết hợp với phương trình đã cho để được một hệ phương trình có vô số nghiệm?

A) x – y = 5

B) –6x + 3y = 15

C) 6x + 15 = 3y

D) 6x – 15 = 3y

Câu 4: Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và tạo thành 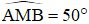 . Khi đó số đo cung bị chắn bở góc ở tâm AOB là bao nhiêu độ?

A) 50^o

B) 40^o

C) 130^o

D) 80^o

II. Tự luận

Bài 1 (2 điểm):

Cho (P) y = x² và đường thẳng (d): y = 2x – 3

a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ

b) Tìm tọa độ giao điểm của (P) và (d)

Bài 2 (2,5 điểm): Giải bài toán bằng cách lập hệ phương trình:

Hai tổ sản xuất cùng nhận chung một đơn hàng, nếu hai tổ cùng làm thì sau 15 ngày sẽ xong. Tuy nhiên, sau khi cùng làm được 6 ngày thì tổ I có việc bận phải chuyển công tác kasc, tổ II làm một mình 24 ngày nữa mới hoàn thành đơn hàng. Hỏi nếu làm một mình thì mỗi tổ làm xong trong bao nhiêu ngày?

Bài 3 (3,5 điểm):

Cho đường tròn (O; R), dây MN không đi qua tâm, C và D là hai điểm bất kỳ thuộc dây MN (C; D không trùng với M, N). A là điểm chính giữa của cung nhỏ MN. Các đường thẳng AC và AD lần lượt cắt (O) tại điểm thứ hai là E; F.

a) Chứng minh 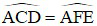  và tứ giác CDEF nội tiếp.

b) Chứng minh: AM² = AC.AE

c) Kẻ đường kính AB. Gọi I là tâm đường tròn ngoại tiếp tam giác MCE. Chứng minh M, I, B thẳng hàng.

Bài 4 (1 điểm): Với x, y, z là các số thực dương thỏa mãn đẳng thức xy + yz + zx = 5

Tìm giá trị nhỏ nhất của biểu thức: 

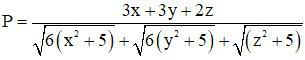
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 2)

Bài 1 (2 điểm): Giải các hệ phương trình sau:

a)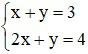  

b)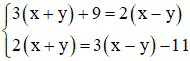  

Bài 2 (1 điểm): Tìm giá trị của a và b để đường thẳng ax – by = 4 đi qua hai điểm A(4; 3) và B(–6; 7).

Bài 3 (2, 5 điểm): Giải bài toán bằng cách lập hệ phương trình:

Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm một mình trong 3 giờ và người thứ hai làm một mình trrong 6 giờ thì được 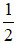  công việc.

Hỏi nếu mỗi người làm một mình thì bao lâu xong công việc.

Bài 4 (3, 5 điểm): Từ một điểm A ở ngoài đường tròn vẻ tiếp tuyến AB và cát tuyến ACD. Tia phân giác của góc BAC cắt BC; BD lần lượt tại M và N. Vẽ dây BF vuông góc với MN cắt MN tại H, cắt CD tại E. Chứng minh:

a) Tam giác ABE cân

b) BF là tia phân giác của góc CBD

c) FD² = FE.FB

Bài 5 (1 điểm): Cho 3 số dương a, b, c thỏa mãn hệ thức: 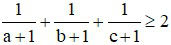. Tìm giá trị lớn nhất của biểu thức: M = abc

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 3)

Bài 1 (2 điểm): Cho hệ phương trình

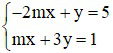
a) Giải hệ phương trình khi m = 2

b) Tìm m để hệ phương trình có nghiệm (x; y) sao cho x; y dương

Bài 2 (2 điểm): Giải bài toán bằng cách lập hệ phương trình

Một mảnh vườn hình chữ nhật có chu vi 34m. Nếu tăng chiều dài thêm 3m và tăng chiều rộng thêm 2m thì diện tích tăng thêm 45m². Hãy tính chiều dài, chiều rộng mảnh vườn.

Bài 3 (2 điểm): Cho hàm số y = ax² 

a) Xác định a biết rằng đồ thị của hàm số đi qua điểm A (3; 3)

b) Tìm giá trị của m, n để các điểm B (2; m); C (n; 1) thuộc đồ thị hàm số trên

Bài 4 (3,5 điểm): Cho nửa đường tròn (O; R) đường kính AB và một điểm C trên nửa đường tròn đó (AC < BC), H là một điểm bất kỳ trên dây BC nhưng khong trùng với B và C; AH cát nửa đường tròn tại điểm thứ hai là D, AC cắt đường thẳng BD tại E

a) Chứng minh tứ giác CHDE nội tiếp

b) Vẽ tiếp tuyến BX của đường tròn (O); Tia CD cắt Bx tại M. Chứng minh: MB² = MC.MD

c) Chứng minh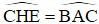  

Bài 5 (0,5 điểm): Chứng minh rằng: 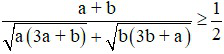  với a, b là các số dương.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 4)

I. Trắc nghiệm (1 điểm)

Câu 1: Hệ phương trình   vô nghiệm khi

A) m = −1

B) m = 1

C) m = −6

D) m = 6

Câu 2: Cặp số (2; -3) là nghiệm của hệ phương trình nào dưới đây

A)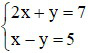  

B)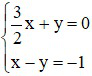  

C)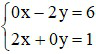  

D)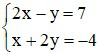  

Câu 3: Cho tứ giác ABCD nội tiếp đường tròn có 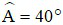; 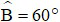. Khi đó bằng  :

A) 30^o

B) 20^o

C) 120^o

D) 140^o

Câu 4: Mệnh đề nào sau đây sai:

A) Hình thang cân nội tiếp được một đường tròn

B) Hai cung có số đo bằng nhau thì bằng nhau

C) Hai cung bằng nhau thì có số đo bằng nhau

D) Hai góc nội tiếp bằng nhau thì cùng chắn một cung

II. Tự luận

Bài 1 (2 điểm):

a) Tính giá trị biểu thức 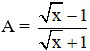  khi x = 9

b) Rút gọn biểu thức 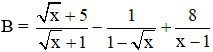  với x ≥ 0; x ≠ 1

c) Tìm x để P = A > B có giá trị nguyên.

Bài 2 (1,5 điểm): Giải các hệ phương trình sau: 

a)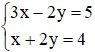  

b)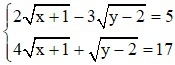  

Bài 3 (1,5 điểm): Giải bài toán bằng cách lập hệ phương trình

Hai vòi nước cùng chảy vào bể có nước thì sau 12 giờ đầy bẻ. Nếu người ta mở cả hai chảy trong 4 giờ rồi khóa vòi thứ 2 lại và để vời một chảy một mình thì sau 14 giờ nữa mới đầy bẻ. Tính thời gian mỗi vòi chảy 1 mình đầy bể.

Bài 4 (3, 5 điểm): Cho đường tròn (O; R) và đường thẳng d không có điểm chung với đường tròn. Từ điểm M thuộc đường thẳng d kẻ hai tiếp tuyến MA, MB với đường tròn. Hạ OH vuông góc với đường thẳng d tại H. Ab cắt OH tại K, cắt OM tại I. Tia OM cắt đường tròn (O; R) tại E.

a) Chứng minh AOBM là tứ giác nội tiếp

b) Chứng minh OI.OM = OK.OH

c) Chứng minh E là đường tròn nội tiếp tam giác MAB

d) Tìm vị trí của điểm M trên đường thẳng d để diện tích tam giác OIK có giá trị lớn nhất.

Bài 5 (0,5 điểm): Cho hai số dương x; y thỏa mãn x + y = 1

Tìm giá trị nhỏ nhất của biểu thức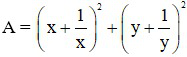  

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 5)

Bài 1 (2 điểm): Giải hệ phương trình:

a)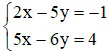  

b)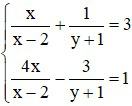  

Bài 2 (2 điểm):

a) Vẽ parabol (P): y = 2x²

b) Viết phương trình đuuờng thẳng (d) cắt (P) tại hai điểm A và B có hoành độ lần lượt là -1 và 2.

Bài 3 (2 điểm): Một tổ theo kế hoạch phải sản xuất 75 thùng khẩu trang trong một số ngày dự định. Trong thực tế, do cải tiến kỹ thuật nên mỗi ngày tổ đã làm vượt mức 5 thùng vì vậy họ đã làm được 80 thùng và hoàn thành trước kế hoạch 1 ngày. Hỏi theo kế hoạch mỗi ngày tổ phải làm bao nhiêu thùng khẩu trang.

Bài 4 (3,5 điểm): Cho đường tròn (O; R). Từ điểm A ngoài đường tròn kẻ hai tiếp tuyến Ab và AC với đường tròn (B, C là các tiếp điểm). Từ B kẻ đường thẳng song song với AC cắt (O) tại D (D khác B), đường thẳng AD cắt (O) tại E (E khác D).

a) Chwunsg minh tứ giác ABOC nội tiếp

b) Chứng minh AE.AD = AB²

c) Chứng minh  

d) Giả sử OA = 3R. Tính khoảng cách giữa hai đường thẳng AC và BD theo R.

Bài 5 (0, 5 điểm): Giải phương trình

 

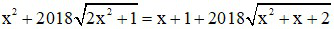
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 6)

Bài 1 (2 điểm): Cho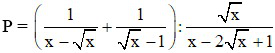  

a) Rút gọn biểu thức P

b) Tính giá trị của P khi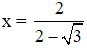  

c) Tìm các giá trị của x để P >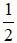  

Bài 2 (2 điểm): Một khi đất hình chữ nhật có chi vi bằng 72m. Nếu tăng chiều rộng lên gấp đôi và chiều dài lên gấp ba thì chu vi của khu vườn mới là 194m. Hãy tính chiều dài, chiều rộng của khu vườn đã cho ban đầu.

Bài 3 (2 điểm): Cho hệ phương trình: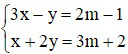  

a) Giải hệ phương trình khi m = 1

b) Tìm m để hệ (1) có cặp nghiệm (x; y) duy nhất thỏa mãn: x² + y² = 5

Bài 4 (1 điểm): Trong hệ tọa độ Oxy, cho đường thẳng (d): y = (a – 2b)x + b. Tìm a, b để (d) đi qua A(1; 2) và B(-4; 3)

Bài 5 (2, 5 điểm): Cho đường tròn o đường kính AB. Vẽ dây CD vuông góc với AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhot BC (E khác B và C). AE cắt CD tại F. Chứng minh:

a) BEFI là tứ giác nội tiếp đường tròn.

b) IA.IB = Ic.ID và AE.AF = AC²

c) Khi E di chuyển trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ACEF luôn thuộc một đường thẳng cố định.

Bài 6 (0,5 điểm): Cho a, b, c, d, e > 0. Chứng minh: 

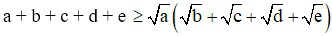
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 7)

I. Trắc nghiệm (1 điểm)

Câu 1: Phương trình x – 3y =0 có nghiệm tổng quát là:

A) (x ∈ R; y = 3x)

B) (x = 3xy; y ∈ R)

C) (x ∈ R; y = 3)

D) (x = 0; y ∈ R)

Câu 2: Giá trị m; n để hệ phương trình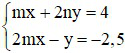  

A) m = 6; n = 2,5

B) m = 6; n = -2,5

C) m = -6; n = -2,5

D) m = -6; n = 2,5

Câu 3: Chu vi đường tròn có bán kinh 4cm là (π = 3,14)

A) 25,12cm

B) 23,12cm

C) 12,56cm

D) 11,56cm

Câu 4: Cho đường tròn (O) đường kính AB, đường thẳng chia dây BD cắt tiếp tuyến tại A ở M ngời đường tròn, số đo cung nhỏ BD bằng 60^o. Số đo góc AMB:

A) 60^o

B) 30^o

C) 120^o

D) 90^o

II. Tự luận

Bài 1 (1,5 điểm): Cho hệ phương trình: 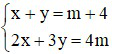  (m là tham số)

a) Giải hệ phương trình khi m = 1

b) Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m.

Bài 2 (2 điểm): Cho biểu thức 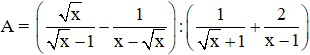  với x > 0, x ≠ 1

a) Rút gọn biểu thức A.

 b) Tính giá trị của A khi x = 2√2 + 3.

Bài 3 (1,5 điểm): Một nhóm gồm 15 học sinh nam và nữa tham gia trồng cây. Cả buổi lao động thầy giáo nhận thấy các bạn nam trồng được 30 cây, các bạn nữ trồng được 36 cây. Mỗi bạn nam trồng được số cây như nhau và mỗi bạn nữ trồng được số cây như nhau. Tính số học sinh nam và học sinh nữ tham gia trồng cây, biết mỗi học sinh nam trồng được nhiều hơn mỗi học sinh nữ 1 cây.

Bài 4 (3, 5 điểm): Cho đường tròn (O; R), dây MN không đi qua tâm, C và D là hai điểm bất kỳ thuộc dây MN (C; D không trùng với M, N). A là điểm chính giữa của cung nhỏ MN. Các đường thẳng AC và AD lần lượt cắt (O) tại điểm thứ hai là E; F.

a) Chứng minh 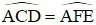  và tứ giác CDEF nội tiếp.

b) Chứng minh: AM² = AC.AE

c) Kẻ đường kính AB. Gọi I là tâm đường tròn ngoại tiếp tam giác MCE. Chứng minh M, I, B thẳng hàng.

Bài 5 (0, 5 điểm): Cho ba số a, b, c > 0. Chứng minh rằng:

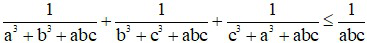
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 8)

Bài 1 (2 điểm): Cho đường thẳng (d): y = x + 2 và parabol (P): y = (2m – 1)x²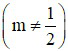   

a) Tìm m biết (P) đi qua điểm M (-2; 4)

b) Với m vừa tìm được:

i) Vẽ đồ thị của (d) và (P) trên cùng một mặt phẳng tọa độ.

ii) Xác định tọa độ giao điểm của (d) và (P).

Bài 2 (2 điểm): Giải phương trình và hệ phương trình

a) x² − 6x + 5 = 0

b)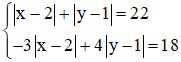  

Bài 3 (2 điểm): Một người đi xe đạp từ A đến B với vận tốc không đổi, hai địa điểm cách nhau 30km. Khi từ B về A người đó chọn đường khác dễ đi hơn nhưng dài hơn con đường cũ 6km. Vì vậy lúc về người đó đi với vận tốc lớn hơn lúc đi là 3km/h. Nên thời gian về vẫn ít hơn thời gian đi 3km. Tính vận tốc ban đầu của người đó.

Bài 4 (3, 5 điểm): Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh AC (M khác A và C). Đường tròn đường kính MC cắt BC tại N và cắt tia BM tại I. Chứng minh rằng :

a) ABNM và ABCI là các tứ giác nội tiếp đường tròn.

b) NM là tia phân giác của góc  .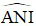

c) BM.BI + CM.CA = AB² + AC².

Bài 5 (0,5 điểm): Tính giá trị nhỏ nhất của biểu thức: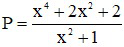  

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 9)

Bài 1 (2 điểm): Cho biểu các biểu thức:

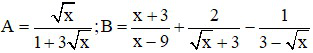  với x > 0; x ≠ 9.

a) Tính A khi x =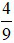  

b) Rút gọn B

c) Cho P = B : A. Tìm x để P < 3

Bài 2 (2 điểm): Giải các phương trình hệ phương trình sau:

a)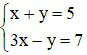  

b) x⁴ − 5x² + 4 = 0

Bài 3 (2 điểm): Một tổ theo kế hoạch phải sản xuất 75 thùng khẩu trang trong một số ngày dự định. Trong thực tế, do cải tiến kỹ thuật nên mỗi ngày tổ đã làm vượt mức 5 thùng vì vậy họ đã làm được 80 thùng và hoàn thành trước kế hoạch 1 ngày. Hỏi theo kế hoạch mỗi ngày tổ phải làm bao nhiêu thùng khẩu trang.

Bài 4 (3, 5 điểm): Cho đường tròn (O; R) có đường kính AB. Vẽ dây cung CD vuông góc với AB (CD không đi qua tâm O). Trên tia đối của tia BA lấy điểm S; SC cắt (O; R) tại điểm thứ hai là M.

a) Chứng minh tam giác SMA đồng dạng với tam giác SBC.

b) Gọi H là giao điểm của MA và BC; K là giao điểm của MD và AB. Chứng minh BMHK là tứ giác nội tiếp và HK // CD. 

c) Chứng minh: OK.OS = R²

Bài 5 (0, 5 điểm): Cho 3 số dương a, b, c thỏa mãn hệ thức:  . Tìm giá trị lớn nhất của biểu thức: M = abc

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 9

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 10)

I. Trắc nghiệm (1 điểm)

Câu 1: Cho đường tròn (O) đường kính AB, đường thẳng chứa dây BD cắt tiếp tuyến tại A ở M ngoài đường tròn, số đo cung nhỏ BD bằng 60^o. Số đo góc AMB là 

A) 60^o

B) 30^o

C) 120^o

D) 90^o

Câu 2: Cho đường tròn (O), T là điểm thuộc đường tròn. Đường thẳng chứa dây AB và tiếp tuyến tại T cắt nhau tại M nằm ngoài đường tròn. Ta có:

A) MT² = MA.MB

B) MB² = MA.MT

C) MA² = MT.MB

D) MT² = MA + MB

Câu 3: Nghiệm của hệ phương trình 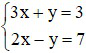  có nghiệm là:

A) (2; 3)

B) (2; -3)

C) (3; 2)

D) (-2; 3)

Câu 4: Hệ phương trình 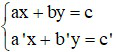  (với a; b; c; a’; b’; c’ khác 0)

Khi nào hệ có vô số nghiệm

A)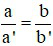  

B)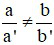  

C)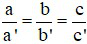  

D)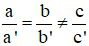  

II. Tự luận

Bài 1 (1,5 điểm): Cho hệ phương trình

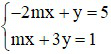
a) Giải hệ phương trình khi m = 2

b) Tìm m để hệ phương trình có nghiệm (x; y) sao cho x; y dương

Bài 2 (2 điểm): Giải các phương trình, hệ phương trình sau:

a)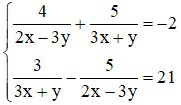  

b) 4x² + 24x − 45 = 0

Bài 3 (1,5 điểm): Một công nhân dự định làm 70 sản phẩm trong thời gian quy định. Nhưng thực tế xí nghiệp đó đã giao cho công nhân phải làm 84 sản phẩm. Mặc dù mỗi giờ người đó đã làm thêm được 1 sản phẩm nhưng vẫn hoàn thành chậm hơn kế hoạch 35 phút. Hỏi theo dự định lúc đầu, trung bình mỗi giờ người đó phải làm bao nhiêu sản phẩm. Biết mỗi giờ người đó làm không quá 10 sản phẩm.

Bài 4 (3, 5 điểm): Cho ba điểm A, B, C cố định thẳng hàng theo thứ tự đó. Vẽ đường tròn (O; R) bất kỳ đi qua B và C (BC ≠ 2R). Từ A kẻ các tiếp tuyến AM, AN đến (O) (M, N là tiếp điểm). Gọi I, K lần lượt là trung điểm của BC và MN; MN cắt BC tại D. Chứng minh:   

a) AM² = AB.AC

b) AMON; AMOI là các tứ giác nội tiếp đường tròn. 

c) Khi đường tròn (O) thay đổi, tâm đường tròn ngoại tiếp ΔOID luôn thuộc một đường thẳng cố định.

Bài 5 (0,5 điểm): Cho a, b, c, d, e > 0. Chứng minh: 

................................

................................

................................

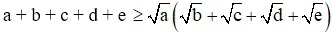
Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 9 năm 2024 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---