Đề thi Học kì 1 Toán lớp 8 có đáp án (6 đề)
Tuyển chọn Đề thi Học kì 1 Toán lớp 8 có đáp án (6 đề) chọn lọc được các Giáo viên nhiều năm kinh nghiệm biên soạn và sưu tầm từ Đề thi Toán 8 của các trường THCS. Hi vọng bộ đề thi này sẽ giúp học sinh ôn tập và đạt kết quả cao trong các bài thi Học kì 1 môn Toán lớp 8.
Đề thi Học kì 1 Toán lớp 8 có đáp án (6 đề)
Để mua trọn bộ Đề thi Toán 8 theo cấu trúc mới bản word có lời giải chi tiết, đẹp mắt, quý Thầy/Cô vui lòng xem thử:
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
năm 2025
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 1)
Câu 1 (1,0 điểm). Thực hiện phép tính.
a) 2x.(x2 - x + 3) b) (3 - 2x)(2x + )
Câu 2 (1,5 điểm). Phân tích các đa thức sau thành nhân tử.
a) 2x2 + 4x
b) 2(x - y) + a(y -x)
c) x2 + y2 - 2xy - 4
Câu 3 (3,0 điểm).
1) Tìm x, biết:
a) 2x2 + x = 0 b) 2x(x - 5) - x(3 + 2x) = 26
2) Tính nhanh: 342 + 162 + 32.
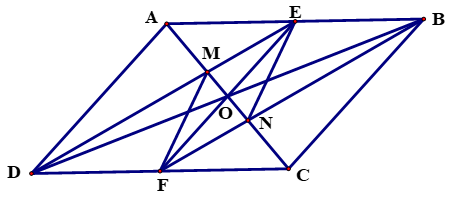
Câu 4 (3,0 điểm). Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.
a) Tứ giác DEBF là hình gì? Vì sao?
b) Chứng minh rằng các đường thẳng AC, BD, EF đồng quy tại một điểm.
c) Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng M và N đối xứng nhau qua O.
Câu 5 (1,0 điểm)
Để đo khoảng cách giữa hai điểm B và C bị ngăn bởi một cái hồ nước, người ta đóng các cọc ở vị trí A, B, C, M, N như hình vẽ. Người ta đo được MN = 55m. Tính khoảng cách BC?
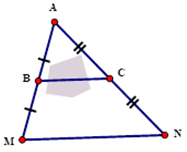
Câu 6 (0,5 điểm)
a) Cho a; b; c thoả mãn: a2022 + b2022 + c2022 = a1011b1011 + b1011c1011 + c1011a1011
Tính giá trị của biểu thức
⇒ 2(a2022 + b2022 + c2022) = 2(a1011b1011 + b1011c1011 + c1011a1011)
b) Cho ba số a, b, c thỏa mãn a + b + c = 0.
Chứng minh rằng: a4 + b4 + c4 = 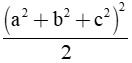
----- HẾT -----
Câu |
Nội dung |
Điểm |
|
1 (1,0 điểm) |
a) 2x.(x2 - x + 3) = 2x3 - 2x2 + 6x |
0,5 |
b) (3 - 2x).(2x + 3) = 9 - 4x2 |
0,5 |
|
|
2 (1,5 điểm) |
a) 2x2 + 4x = 2x(x + 2) |
0.5 |
|
b) 2(x - y) + a(y - x) = 2(x - y) - a(x - y) = (2 - a)(x - y) |
0.25 0.25 |
|
|
c) x2 + y2 - 2xy - 4 = (x2 + y2 - 2xy) - 4 = (x - y - 2)(x - y + 2) |
0.25 0.25 |
|
|
3 (3,0 điểm) |
1) (1,5 điểm) a) 2x2 + x = 0 ⇒ x(2x + 1) = 0
Vậy |
0.25 0.5 0.25 |
|
b) 2x(x - 5) - x(3 + 2x) = 26 ⇒ 2x2 - 10x - 3x -2x2 = 26 ⇒ -13x = 26 ⇒ x = -2 Vậy x = -2 |
0.25 0.5 0.25 |
|
|
2) (1 điểm) 342 + 162 + 32.34 = 342 + 162 + 2.16.34 = (34 + 16)2 = 502 = 2500 |
0.25 0.5 0,25 |
|
|
4 (3.0 điểm) |
- Vẽ hình đúng để làm được ý a
|
0,25 |
|
a) (1 điểm) - Chỉ ra được tứ giác DEBF là hình bình hành |
1.0 |
|
|
b) (0,75 điểm). Gọi O là giao điểm của AC và BD - Chỉ ra trong hbh ABCD có O là trung điểm O của AC và BD (1) - Chỉ ra trong hbh có BD cắt EF tại trung điểm của mỗi đường. Mà O là trung điểm của BD nên O là trung điểm của EF (2) - Từ (1) và (2) ⇒ đpcm |
0.25 0.25 0.25 |
|
|
c) (1 điểm) - Chỉ ra được M là trọng tâm của ΔABD ⇒ OM = - Chỉ ra được N là trọng tâm của ΔBCD ⇒ ON = - Mà OA = OC ⇒ OM = ON ⇒ đpcm |
0.25 0.25 0.25 0.25 |
|
|
5 (1,0 điểm) |
- Chỉ ra được BC là đường trung bình của tam giác AMN - Tính được BC = 27,5m |
0,5 0,5 |
|
6 (0,5 điểm) |
a) (0,25 điểm) Từ: a2022 + b2022 + c2022 = a1011b1011 + b1011c1011 + c1011a1011 ⇒ 2(a2022 + b2022 + c2022) = 2(a1011b1011 + b1011c1011 + c1011a1011) ⇒ (a1011 - b1011)2 + (b1011 - c1011)2 + (c1011 - a1011)2 ⇒ a = b = c ⇒ A = (a - b)2020 + (b - c)2021 + (a - c)2022 = 0 |
0.25 |
|
b) (0,25 điểm) Vì a + b + c = 0 ⇒ (a + b + c)2 = 0 ⇒ a2 + b2 + c2 + 2(ab + bc + ca) = 0 ⇒ a2 + b2 + c2 = - 2(ab + bc + ca) ⇒ (a2 + b2 + c2)2 = 4(ab + bc + ca)2 ⇒ a4 + b4 + c4 + 2(a2b2 + b2c2 + c2a2) = 4(a2b2 + b2c2 + c2a2) + 8abc(a + b + c) ⇒ a4 + b4 + c4 + 2(a2b2 + b2c2 + c2a2) + 8abc.0 (do a + b + c = 0) ⇒ 2(a4 + b4 + c4) = a4 + b4 + c4 + 2(a2b2 + b2c2 + c2a2) ⇒ 2(a4 + b4 + c4) = (a2 + b2 + c2)2 ⇒ a4 + b4 + c4 = |
0,25 |
Học sinh làm bằng cách khác đúng thì cho điểm tương tự

Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
năm 2025
Bài thi môn: Toán lớp 8
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 2)
Bài 1. (2 điểm) Phân tích đa thức thành nhân tử:
a) x2 - 4y2 - 2x + 4y b) (x2 + 2x)(x2 + 2x - 2) - 3
Bài 2. (0,5 điểm): Cho x + 2y = 5. Tính giá trị của biểu thức
A = x2 + 4y2 - 2x + 10 + 4xy - 4y
Bài 3. (2 điểm): Cho 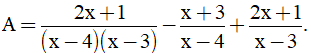
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức A biết x2 = 9.
c) Tìm giá trị nhỏ nhất của B biết B = A.(x2 – 5x + 4).
Bài 4. (2 điểm): a) Tìm đa thức thương và đa thức dư trong phép chia sau:
(2x3 – 7x2 + 13x + 2) : (2x – 1).
b) Xác định số hữu tỉ a để f(x) = x3 – 2x2 + 5x + a chia hết cho đa thức g(x) = x – 3.
Bài 5. (3 điểm) Cho hình thoi ABCD có góc A bằng 600, kẻ BH vuông góc với AD tại H. Gọi O là giao điểm của AC và BD; E là điểm đối xứng của B qua H; F là điểm đối xứng của C qua B.
a) Tứ giác ABDE là hình gì? Vì sao?
b) Chứng minh tứ giác ABCE là hình thang cân.
c) Kẻ AK ⊥ OE tại K. Gọi L là trung điểm của đoạn EK. Chứng minh AL // FK.
Bài 6. (0,5 điểm) Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
năm 2025
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 3)
Câu 1: (1,0 điểm)
a. Nêu tính chất đường trung bình của tam giác?
b. Cho ΔABC. Gọi M là trung điểm của AB, N là trung điểm của AC, biết BC = 10cm. Tính MN.
Câu 2: (2,0 điểm) Phân tích các đa thức sau thành nhân tử.
a. 3a + 3b – a2 – ab
b. x2 + x + y2 – y – 2xy
c. - x2 + 7x – 6
Câu 3: (2,0 điểm) Thực hiện phép tính.
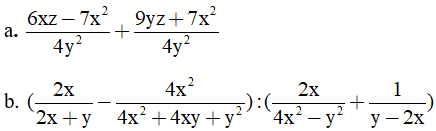
Câu 4: (2,0 điểm) Cho phân thức A = 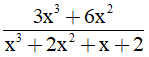
a/ Tìm điều kiện của x để giá trị của phân thức xác định.
b/ Tìm giá trị của x để phân thức có giá trị bằng 2.
Câu 5: (3,0 điểm) Cho ΔABC vuông tại A (AB < AC). Gọi I là trung điểm BC. Qua I vẽ IM ⊥ AB tại M và IN ⊥ AC tại N.
a. Tứ giác AMIN là hình gì? Vì sao?
b. Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.
c. Đường thẳng BN cắt DC tại K. Chứng minh 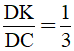 .
.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
năm 2025
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 4)
I. Phần trắc nghiệm: (3 điểm)
Câu 1: (1 điểm) Điền chữ Đ hoặc chữ S trong ô vuông tương ứng với mỗi phát biểu sau:
a. ( x + 5 )( x – 5 ) = x2 – 5
b. a3 – 1 = (a – 1 ) ( a2 + a + 1 )
c. Hình bình hành có một tâm đối xứng là giao điểm của hai đường chéo
d. Hai tam giác có diện tích bằng nhau thì bằng nhau
Câu 2: (2 điểm) Khoanh tròn chữ cái trước câu trả lời đúng nhất:
1. Đa thức x2 – 4x + 4 tại x = 2 có giá trị là:
A. 1 B. 0 C. 4 D. 25
2. Giá trị của x để x ( x + 1) = 0 là:
A. x = 0 B. x = - 1 C. x = 0; x = 1 D. x = 0; x = -1
3. Một hình thang có độ dài hai đáy là 6 cm và 10 cm. Độ dài đường trung bình của hình thang đó là :
A. 14 cm B. 7 cm C. 8 cm D. Một kết quả khác.
4. Một tam giác đều cạnh 2 dm thì có diện tích là:
A. √3 dm2 B. 2√3 dm2 C. 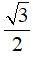 dm2 D. 6dm2
dm2 D. 6dm2
II. Phần tự luận: (7 điểm)
Bài 1: (1,5 điểm) Tính:
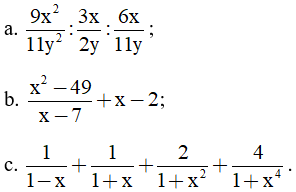
Bài 2: (1,5 điểm) Cho phân thức: A = 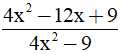
a) Tìm điều kiện xác định của phân thức A.
b) Thu gọn biểu thức A
c) Tính giá trị của biểu thức A với 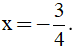 .
.
Bài 3: (3,5 điểm) Cho ΔABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ HE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25 cm.
a) Tính độ dài cạnh AC và diện tích tam giác ABC
b) Chứng minh tứ giác ADHE là hình chữ nhật
c) Trên tia đối của tia AC lấy điểm F sao cho AF = AE. Chứng minh tứ giác AFDH là hình bình hành
d) Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh: CM ⊥ HK
Bài 4: (0,5 điểm) Cho các số x, y thoả mãn đẳng thức
5x2 + 5y2 + 8xy - 2x + 2y + 2 = 0 Tính giá trị của biểu thức
M = (x + y)2007 + (x - 2)2008 + (y + 1)2009
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
năm 2025
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 5)
I. Trắc nghiệm (2 điểm)
Câu 1. Tìm x, biết: x3 + 4x + x2 + 4 = 0.
A. x = 0
B. x = 2
C. x = -2
D. x = - 1
Câu 2. Tính chất nào dưới đây không phải của hình bình hành:
A. Tổng bốn góc bằng 3600.
B. Hai đường chéo bằng nhau.
C. Các cặp cạnh đối bằng nhau.
D. Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Câu 3. Hình thoi có độ dài hai đường chéo là 10cm và 24cm. Tính chu vi của hình thoi?
A. 12 cm
B. 5 cm
C. 13 cm
D. 26 cm
Câu 4. Có bao nhiêu số tự nhiên n để đa thức 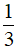 x4yn - x3y2 chia hết cho đơn thức -3xny2
x4yn - x3y2 chia hết cho đơn thức -3xny2
A. 0
B. 2
C. 1
D. 3
II. Tự luận (8 điểm)
Câu 1: (1,0 điểm) Thực hiện phép tính
a) (x + 5)2 - x(x + 10)
b) (18x6y6 - 12x5y5 + 24x3y5) : 6x3y5
Câu 2: (1,5 điểm) Phân tích đa thức sau thành nhân tử
a) a2 - b2 - 12a + 12b
b) 4x2 - 4x + 1 -25y2
c) x2 - 3x - 10
Câu 3: (2,0 điểm) Cho phân thức  với x ≠ 2
với x ≠ 2
a) Rút gọn A
b) Tìm x nguyên để A có giá trị nguyên.
Câu 4: (3,5 điểm) Cho hình chữ nhật ABCD. Gọi M là trung điểm của BC và E là giao điểm của đường thẳng AM với đường thẳng DC.
a) Chứng minh rằng: tứ giác ABEC là hình bình hành
b) Gọi F là điểm đối xứng của B qua C. Chứng minh rằng: tứ giác BEFD là hình thoi.
c) Chứng minh rằng: C là trọng tâm tam giác AEF
d) Cho AB2 = 3BC2. Gọi H là trung điểm của DF và K là giao điểm của đường thẳng AH với đường thẳng EF. Chứng minh rằng: AE = 2MK.
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
năm 2025
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 6)
I. Trắc nghiệm (3 điểm) Hãy chọn và ghi lại chữ cái đứng trước câu trả lời đúng vào bài làm
Câu 1. Số dư khi chia đa thức x2 + 2x + 3 cho đa thức x + 1 là:
A. – 2 B. 1 C. 2 D. 0
Câu 2. Khẳng định nào sau đây là sai?
A. Hình thang có hai cạnh bên bằng nhau là hình thang cân.
B. Hai tam giác bằng nhau có diện tích bằng nhau.
C. Tứ giác có các cạnh đối song song là hình bình hành.
D. Hình thoi có một góc vuông là hình vuông.
Câu 3. Kết quả của phép tính 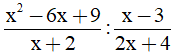 là:
là:
A. 2x – 6 B. x – 3 C. 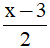 D. 6 – 2x
D. 6 – 2x
Câu 4. Giá trị của phân thức 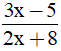 được xác định khi:
được xác định khi:
A. x ≠ 4 B. x ≠ 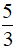 C. x ≠ -4 D. x ≠ -
C. x ≠ -4 D. x ≠ -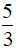
Câu 5. Hình nào dưới đây không có trục đối xứng:
A. Hình thoi B. Hình vuông C. Hình chữ nhật D. Hình bình hành
Câu 6. Giá trị lớn nhất của 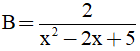 là:
là:
A. 2 B. 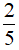 C. 4 D.
C. 4 D. 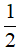
II. Tự luận (7 điểm)
Bài 1. (2 điểm) Cho biểu thức A = 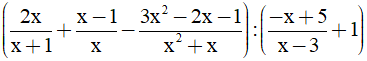
a) Tìm điều kiện xác định của A. Chứng tỏ 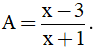
b) Tính giá trị của A biết |x + 2| = 1.
c) Tìm x để 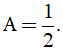
Câu 2: (1,5 điểm) Tìm x, biết:
a) 5x(x - 3) - x2 + 9 = 0
b) x + 4x2 + 4x3 = 0
c) 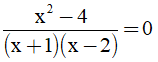
Bài 3: (3,5 điểm) Cho tam giác ABC cân tại A, đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua điểm O.
a) Chứng minh tứ giác AECD là hình chữ nhật.
b) Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE.
c) Cho AB = 10 cm, BC = 12 cm. Tính diện tích tam giác OAD.
d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để tứ giác AEDK là hình thang cân.
................................
................................
................................
Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 8 năm 2026 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Bộ đề thi năm 2025 các lớp các môn học được Giáo viên nhiều năm kinh nghiệm tổng hợp và biên soạn theo Thông tư mới nhất của Bộ Giáo dục và Đào tạo, được chọn lọc từ đề thi của các trường trên cả nước.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

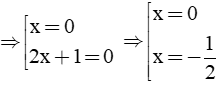
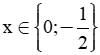
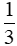 OA
OA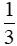 OC
OC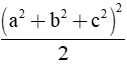






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

