Bộ 10 Đề thi Toán 8 Giữa kì 2 năm 2024 tải nhiều nhất

Với Bộ 10 Đề thi Toán 8 Giữa kì 2 năm 2024 tải nhiều nhất, chọn lọc giúp học sinh ôn tập và đạt kết quả cao trong bài thi Giữa kì 2 Toán 8.

Bộ 10 Đề thi Toán 8 Giữa kì 2 năm 2024 tải nhiều nhất

Xem thử

Chỉ từ 150k mua trọn bộ 100 Đề thi Giữa kì 2 Toán 8 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 1)

I. Trắc nghiệm (3 điểm): Khoanh vào chữ cái đặt trước câu trả lời đúng.

Câu 1: Phương trình bậc nhất một ẩn có dạng nào sau đây?

A. ax + b = 0

B. ax + b > 0

C. ax + b < 0

D. ax + b ≠ 0

Câu 2: Tập nghiệm của phương trình (x + 2)(x – 3) = 0 là:

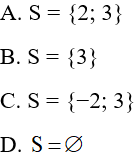
Câu 3: Chia hai vế của phương trình: 

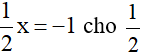
ta được phương trình nào sau đây?

A. x = 2

B. x = 1

C. x = −1

D. x = −2

Câu 4: Phương trình x – 1 = 0 có mấy nghiệm?

A. Một nghiệm

B. Hai nghiệm

C. Vô nghiệm

D. Vô số nghiệm.

Câu 5: Điều kiện xác định của phương trình:

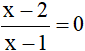
A. x ≠ 2

B. x ≠ 1

C. x ≠ −2

D. x ≠ −1

Câu 6: Nếu AB = 2 m, CD = 4 dm thì:

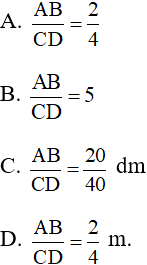
Câu 7: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’và C’D’ nếu có tỉ lệ thức:

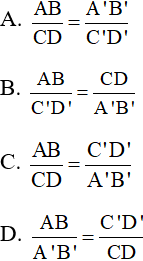
Câu 8: Cho tam giác ABC và tam giác A’B’C’ có

Để tam giác ABC đồng dạng với tam giác A’B’C’ thì góc C =?

A. 30^o 

B. 60^o 

C. 40^o 

D. 50^o.

II. Tự luận:

Bài 1 (1,5 điểm): Giải các phương trình sau:

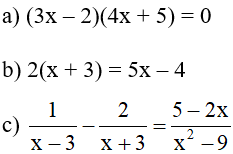
Bài 2 (2 điểm): Một ca nô xuôi dòng từ bến A đến bến B mất 8 giờ và ngược dòng từ bến B về bến A mất 10 giờ. Tính khoảng cách giữa hai điểm A và B, biết rằng vận tốc của dòng nước là 4 km/h.

Bài 3 (3 điểm): Cho ∆ABC có:

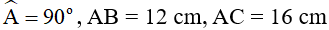
Kẻ đường cao AH (H ∈ BC ), tia phân giác góc A cắt BC tại D.

a) Chứng minh ∆HBA đồng dạng với ∆ABC và AB² = BH.BC

b) Tính độ dài BC, BD và CD.

c) Tính tỉ số diện tích tam giác ABD và tam giác ACD.

d) Từ D kẻ DE vuông góc với AC (E ∈ AC). Tính độ dài đoạn DE.

Bài 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức:

P = 8x² + 3y² – 8xy – 6y + 21.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 2)

I. Trắc nghiệm (3 điểm): Khoanh vào chữ cái đặt trước câu trả lời đúng.

Câu 1: Tập nghiệm của phương trình 2x – 7 = 5 – 4x là:

A. S = {–2}

B. S = {–1}

C. S = {2}

D. S = {1}

Câu 2: Với giá trị nào của m thì phương trình m(x – 3) = 8 có nghiệm x =  –1 ?

A. m = 2 

B. m = – 2

C. m = 3

D. m = – 3.

Câu 3: Cho biết:

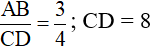
thì độ dài của AB là:

A. 16 cm

B.12 m

C. 9 cm 

D. 6 cm.

Câu 4: Cho tam giác ABC và tam giác DEF có góc A = góc D, Góc B = góc E. AB = 8 cm, BC =  10 cm, DE = 4 cm thì EF bằng:

A. 8cm

B. 4cm

C. 6cm

D. 5cm

Câu 5: Cho tam giác ABC có AM là tia phân giác của góc BAC (M ∈ BC). Chọn khẳng định đúng trong các khẳng định sau:

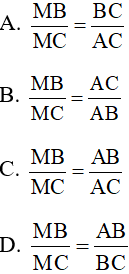
Câu 6: Cho hình vẽ, khẳng định nào sau đây là đúng? 

         

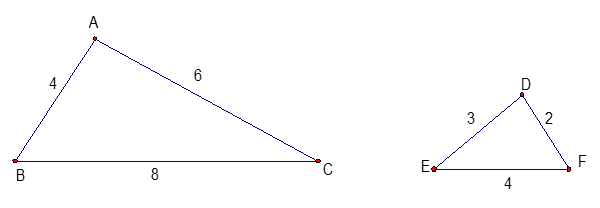
A. Tam giác ABC đồng dạng với tam giác DEF

B. Tam giác ACB đồng dạng với tam giác DFE

C. Tam giác ABC đồng dạng với tam giác DFE

D. Tam giác ACB đồng dạng với tam giác EDF

II. Tự luận:

Bài 1 (2 điểm): Cho hai biểu thức:

a) Tính giá trị của biểu thức B tại x = 2.

b) Rút gọn biểu thức A.

c) Tìm giá trị nguyên của x để P = A.B đạt giá trị nguyên.

Bài 2 (1,5 điểm): Thùng dầu A chứa gấp đôi thùng dầu B. Nếu lấy bớt 20 lít ở thùng A và đổ thêm vào thùng B là 10 lít thì số lít dầu trong thùng A bằng số lít dầu ở thùng B. Tính xem lúc đầu mỗi thùng có bao nhiêu lít dầu?

Bài 3 (3 điểm): Cho tam giác ABC vuông tại A có AH là đường cao (H thuộc BC). Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Chứng minh rằng:

a) AEHD là hình chữ nhật.

b) ∆ABH đồng dạng ∆BHD.

c) HE² = AE.EC.

d) Gọi M là giao điểm của BE và CD. Chứng minh: ∆DBM đồng dạng ∆ECM.

Bài 4 (0,5 điểm): Giải phương trình: 

|x – 2017| + |2x – 2018| + |3x – 2019| = x – 2020.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 3)

I. Trắc nghiệm (3 điểm): Khoanh vào chữ cái đặt trước câu trả lời đúng.

Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là:

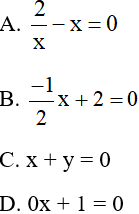
Câu 2: Điều kiện xác định của phương trình:

A. x ≠ 0                 

B. x ≠ 0; x≠ 2                  

C. x≠ 0; x ≠ −2                

D. x ≠ −2

Câu 3: Tập nghiệm của phương trình 2x – 7 = 5 – 4x là:

A. S = {−2}

B. S = {−1}

C. S = {2}

D. S = {1}.

Câu 4: Với giá trị nào của m thì phương trình m(x – 3) = 8 có nghiệm x =  –1 ?

A. m = 2                

B. m = – 2             

C. m = 3                

D. m = – 3.

Câu 4: Cho tam giác ABC đồng dạng với tam giác A’B’C’biết AB = 3 cm, BC = 4 cm, A’B’ = 6 cm, A’C’ = 5 cm. Khi đó ta có:

A. AC = 8 cm; B’C’ = 2,5 cm

B. AC = 2,5 cm; B’C’= 10 cm

C. AC = 2,5 cm; B’C’= 8 cm

D. AC = 10 cm; B’C’= 2 cm.

Câu 6: Chọn câu trả lời đúng. Cho hai tam giác MNP và QRS đồng dạng với nhau theo tỷ số k. Tỷ số chu vi của hai tam giác đó là:

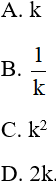
II. Tự luận:

Bài 1 (2 điểm): Giải phương trình: 

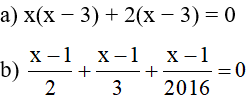
Bài 2 (2 điểm): Một người khởi hành từ A lúc 7 giờ sáng và dự định tới B lúc 11 giờ 30 phút cùng ngày. Do đường chưa tốt nên người ấy đã đi với vận tốc chậm hơn dự định 5 km/h. Vì thế phải 12 giờ người ấy mới đến B. Tính quãng đường AB.

Bài 3 (2,5 điểm): Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm, vẽ đường cao AE.

a) Chứng minh rằng DABC đồng dạng với DEBA.

b) Tia phân giác của góc ABC cắt AC tại F. Tính BF.

Bài 4 (0,5 điểm): Giải phương trình sau:

(2020 – x)³ + (2021 – x)³ + (2x – 4041)³ = 0.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 4)

I. Trắc nghiệm (3 điểm): Khoanh vào chữ cái đặt trước câu trả lời đúng.

Câu 1: Phương trình nào sau đây tương đương với phương trình 2x – 6 = 0?

A. x = 3

B. x = –3

C. x = 2

D. x = –2 

Câu 2: Điều kiện xác định của phương trình:

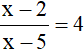
A. x ≠ 2

B. x ≠ 5

C. x ≠ –2

D. x ≠ –5.

Câu 3: Chọn câu trả lời đúng:

A. Hai tam giác vuông bằng nhau thì đồng dạng với nhau.          

B. Hai tam giác vuông đồng dạng thì chu vi bằng nhau

C. Hai tam giác vuông bằng nhau thì đồng dạng với nhau.          

D. Hai tam giác vuông đồng dạng thì diện tích bằng nhau

Câu 4:   Phương trình 5x + 1 = 0 có nghiệm là:

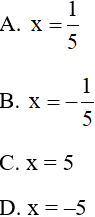
Câu 5: Giá trị x = – 4 là nghiệm của phương trình nào trong các phương trình sau:

A. – 2,5x + 1 = 11 

B. – 2,5x = –10 

C. 3x – 8 = 0

D. 3x – 1 = x + 7

Câu 6: Chọn câu trả lời đúng. 

Cho hai tam giác ABC và DEF có góc A = góc D = 90 độ , AC = 3cm; BC = 5cm; EF = 10cm; DF = 6cm thì:

A. ∆ABC đồng dạng ∆DEF

B. ∆ABC đồng dạng ∆EDF

C. ∆ABC đồng dạng ∆DFE

D. ∆ABC đồng dạng ∆FDE

II. Tự luận: 

Bài 1 (2,5 điểm): Giải các phương trình sau: 

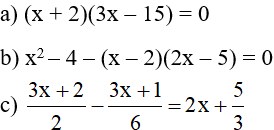
Bài 2 (2 điểm): Một người đi xe máy từ A đến B với vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h nên thời gian về ít hơn thời gian đi là 20 phút. Tính quãng đường AB?

Bài 3 (2 điểm): Cho tam giác ABC vuông tại A có AB = 8cm, AC = 6cm. AD là tia phân giác góc A ( D ∈ BC ) 

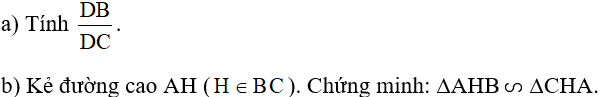
Bài 4 (0,5 điểm): Tìm các số dương a, b thỏa mãn a³ + b³ + 27 = 9ab.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 5)

Bài 1: (3,0 điểm): Giải các phương trình sau:

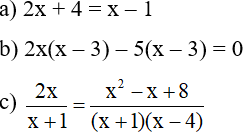
Bài 2: (3,0 điểm): Giải bài toán sau bằng cách lập phương trình:

Một đội công nhân dự định trong một ngày sửa được 40m đường. Nhưng do thời tiết không thuận lợi nên thực tế mỗi ngày họ sửa được một đoạn ít hơn 10m so với dự định và vì vậy họ phải kéo dài thời gian làm việc thêm 6 ngày. Tính chiều dài đoạn đường đội công nhân dự định sửa.

Bài 3: (3,5 điểm): Cho tam giác ABC, điểm D thuộc cạnh BC sao cho BC = 4BD. Điểm E thuộc đoạn thẳng AD sao cho AE = 2ED, BE cắt AC tại K. Kẻ DN song song với BK, N thuộc AC và kẻ KH song song với BC, H thuộc AD.

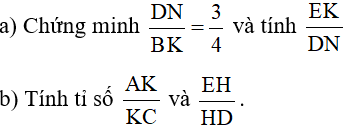
Bài 4: (0,5 điểm): Cho x, y, z > 0 và 4x + 2y + 3z = 9. 

Tìm giá trị nhỏ nhất của P:

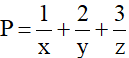
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 6)

Bài 1: (3 điểm): Giải các phương trình sau: 

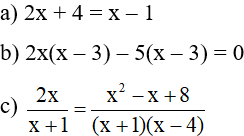
Bài 2 (3 điểm): Giải bài toán bằng cách lập phương trình.

Một người đi xe máy từ A đến B với vận tốc trung bình là 15 km/h. Lúc về người đó đi với vận tốc trung bình là 12 km/h, nên thời gian về nhiều hơn thời gian đi là 22 phút. Tính độ dài quãng đường từ A đến B. 

Bài 3 (3,5 điểm): Cho tam giác nhọn ABC (AB < AC) có ba đường cao AD, BE, CF cắt nhau tại H. 

a) Chứng minh: ∆BFH đồng dạng với ∆CEH và FA.BH = FH.AC.

b) Gọi I là trung điểm của BC và K là điểm đối xứng H qua I. Chứng minh: ∆AKC đồng dạng với ∆AHF.

c) AK cắt HC tại O. Lấy điểm M thuộc đoạn thẳng AC sao cho EF // OM. Chứng minh: HM ⊥ AD.

Bài 4 (0,5 điểm): Giải phương trình sau: (x – 6)⁴ + (8 – x)⁴ = 16.

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 7)

Bài 1 (1,5 điểm): Cho biểu thức:

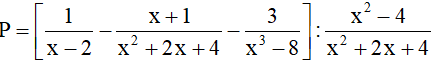
Rút gọn P và tìm x để P nhận giá trị dương.

Bài 2: (3 điểm): Giải các phương trình sau:

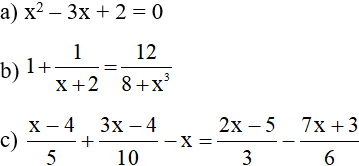
Bài 3 (2 điểm): Một xe máy đi từ tỉnh A đến tỉnh B theo một đường dài 70km. Lúc về, xe máy đi đường khác dài 84km với vận tốc kém lúc đi là 8km/h. Tính vận tốc lúc về của xe máy, biết thời gian phúc về gấp rưỡi thời gian lúc đi. 

Bài 4 (3 điểm): Cho tam giác AOB có AB = 18 cm, OA = 12 cm, OB = 9 cm. Trên tia đối tia OB lấy điểm D sao cho OD = 3 cm. Qua D kẻ đường thẳng song song với AB cắt tia AO tại C. Gọi F là giao điểm của AD và BC.

a) Tính độ dài OC, CD.

b) Chứng minh FD.BC = FC.AD.

c) Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M, N. Chứng minh OM = ON.

Bài 5 (0,5 điểm): Cho x, y, z > 0 thỏa mãn xy + yz + xz = 0,25.

Tìm giá trị nhỏ nhất của Q = 36(x² + y²) + z².

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 8)

Bài 1 (3 điểm): Giải các phương trình sau: 

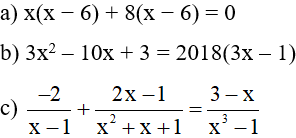
Bài 2 (3 điểm): Một học sinh đi xe đạp từ nhà đến trường với vận tốc 15km/h. Lúc về nhà đi với vận tốc 12km/h nên thời gian về nhiều hơn thời gian đi là 10 phút. Tính quãng đường từ nhà đến trường.

Bài 3 (3,5 điểm): Cho hình vuông ABCD, AB = 4 cm. Trên đoạn BC lấy điểm M sao cho CM = 1 cm. AM kéo dài cắt CD tại điểm E.

a) Tính tỉ số CE/AB và độ dài đoạn thẳng AE. 

b) Kẻ BK vuông góc với AE tại K và MH vuông góc với BE tại H. Chứng minh BK và MH cắt nhau tại một điểm thuộc BC.

c) Chứng minh hai tam giác MBK, MCE đồng dạng và góc MKC = góc MFC.

Bài 4 (0,5 điểm): Giải phương trình: 

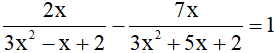
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 9)

Bài 1 (1,5 điểm): Rút gọn biểu thức:

 

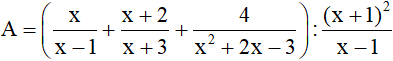
và tìm x để A > 1.

Bài 1 (3 điểm): Giải các phương trình sau:

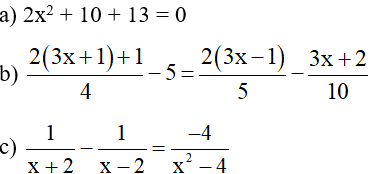
Bài 2 (2 điểm): Một đội sản xuất dự định mỗi ngày làm được 50 chi tiết máy. Khi thực hiện mỗi ngày đội làm được 60 chi tiết máy. Vì vậy đội không những đã hoàn thành xong trước kế hoạch 4 ngày mà còn làm thêm được 60 chi tiết máy. Tính số chi tiết máy thực tế đội sản xuất được.

Bài 3 (3 điểm): ChoABC vuông tại A có AB = 15, AC = 20 và đường cao AH.

a) Chứng minh: Tam giácABC đồng dạng với tam giác HAC. 

Từ đó suy ra: AC²= BC.HC.

b) Chứng minh: AH²= BH.CH.

c) Tính độ dài trung tuyến AM và đường cao AH của ∆ABC.

Bài 4 (0,5 điểm): Giải phương trình: 

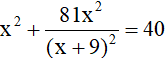
Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 8

Thời gian làm bài:90 phút

(không kể thời gian phát đề)

(Đề số 10)

Bài 1 (1,5 điểm): Xác định m để điều kiện xác định của phương trình : 

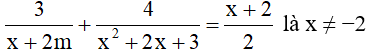
Bài 2 (3 điểm): Giải các phương trình sau:

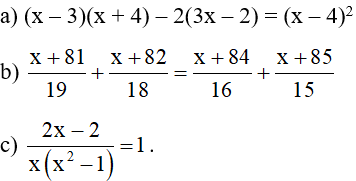
Bài 3 (2 điểm): Một mảnh đất hình chữ nhật có chu vi là 28 mét, độ dài đường chéo bằng 10 mét. Tính chiều dài, chiều rộng của mảnh đất đó theo mét.

Bài 4 (3 điểm): Cho tam giác ABC nhọn, AB < AC, các đường cao AD, BE, CF đồng quy tại trực tâm H.

a) Chứng minh HE.HB = HF.HC.

b) Chứng minh AF.AB = AE.AC = AH.AD và góc AFE = góc ACB = góc AHE.

c) AH cắt EF tại I. Chứng minh IA.IH = IE.IF.

Bài 5 (0,5 điểm): Giải phương trình: 

................................

................................

................................

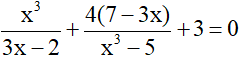
Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 8 năm 2024 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---