Đề kiểm tra Toán 7 Chương 3 Hình học có đáp án, cực hay (210 đề)

Để ôn luyện và làm tốt các bài kiểm tra Toán lớp 7, dưới đây là Top 24 Đề kiểm tra Toán 7 Chương 3 Hình học có đáp án, cực hay. Hi vọng bộ đề kiểm tra này sẽ giúp bạn ôn luyện & đạt điểm cao trong các bài kiểm tra Toán lớp 7.

Quảng cáo

Phòng Giáo dục và Đào tạo .....

Đề kiểm tra 15 phút Chương 3 Hình học (phần Quan hệ giữa các yếu tố trong tam giác)

Môn: Toán lớp 7

Thời gian làm bài: 15 phút

(Trắc nghiệm + Tự luận)

A. Phần trắc nghiệm (4 điểm)

Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:

Câu 1: Cho tam giác ABC có độ dài các cạnh AB = 4cm, AC = 3cm, BC = 3cm. Góc lớn nhất của tam giác là:

A. Góc A B. Góc B

C. Góc C D. Góc B và góc A

Câu 2: Tam giác cân có độ dài hai cạnh là 3cm, 7cm. Khi đó độ dài cạnh còn lại là:

A. 4cm B. 3cm C. 7cm D. 5cm

Câu 3: Cho tam giác ABC có ∠A = 90^o, ∠B = 30^o. Cạnh lớn nhất của tam giác là:

A. Cạnh AB B. Cạnh BC.

C. Cạnh CA D. AB và CA

Câu 4: Cho tam giác ABC có độ dài các cạnh AB = 8cm, AC = 7cm, BC = 4cm. So sánh các góc của tam giác ABC.

A. ∠B > ∠A > ∠C B. ∠C < ∠B < ∠A

C. ∠C > ∠A > ∠B D. ∠C > ∠B > ∠A

B. Phần tự luận (6 điểm)

Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA

a. Chứng minh ΔAMB = ΔDMC

b. Chứng minh AC > CD

c. So sánh ∠(BAM) và ∠(MAC)

Quảng cáo

Đáp án và thang điểm

A. Phần trắc nghiệm (4 điểm)

Mỗi câu trả lời đúng được 1 điểm

1	2	3	4
C	C	B	D

Câu 1: Vì cạnh AB là cạnh lớn nhất nên góc C là góc lớn nhất. Chọn C

Câu 2: Theo bất đẳng thức tam giác, cạnh còn lại lớn hơn 4cm và nhỏ hơn 10cm mà tam giác là tam giác cân nên chọn C

Câu 3: Tam giác ABC là tam giác vuông nên góc A là góc lớn nhất, suy ra cạnh lớn nhất là BC. Chọn B

Câu 4: Vì BC < AC < AB ⇒ ∠A < ∠B < ∠C hay ∠C > ∠B > ∠A . Chọn D

B. Phần tự luận (6 điểm)

a. Hình vẽ (1 điểm)

Đề kiểm tra Toán 7 có đáp án và thang điểm | Đề kiểm tra 15p, 1 tiết Toán 7 Đại số và Hình học

Xét ΔABM và ΔBCM có:

BM = MC

∠(AMB) = ∠(BMC)

AM = MD

⇒ ΔABM = ΔBCM (c.g.c) (1 điểm)

b. Vì ΔABM = ΔBCM ⇒ AB = DC mà AB < AC ⇒ CD < AC (2 điểm)

c. Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (1 điểm)

Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM) (0.5 điểm)

Suy ra ∠(MAB) > ∠(MAC) (0.5 điểm)

Phòng Giáo dục và Đào tạo .....

Đề kiểm tra 15 phút Chương 3 Hình học (phần Các đường đồng quy của tam giác)

Môn: Toán lớp 7

Thời gian làm bài: 15 phút

(Trắc nghiệm + Tự luận)

A. Phần trắc nghiệm (4 điểm)

Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:

Câu 1: Cho tam giác ABC vuông tại A, AI là tia phân giác của góc A. Khi đó số đo góc (BAI) là:

A. 15^o B. 45^o C. 90^o D. 35^o

Quảng cáo

Câu 2: Cho tam giác ABC, điểm M nằm trên trong tam giác ABC sao cho MA = MB. Khẳng định nào sau đây đúng về vị trí điểm M

A. M thuộc tia phân giác của góc BCA

B. M thuộc đường cao của tam giác ABC kẻ từ C

C. M thuộc đường trung tuyến của tam giác ABC kẻ từ C

D. M thuộc đường trung trực của AB

Câu 3: Cho tam giác ABC có AH là đường cao kẻ từ A. Biết góc B bằng 50^o. Khi đó số đo góc (BAH) là:

A. 40^o B. 50^o C. 45^o D. 60^o

Câu 4: Cho tam giác ABC có đường phân giác của góc B và C cắt nhau tại P. Khi đó AP là:

A. Đường phân giác của góc A

B. Đường trung tuyến kẻ từ A

C. Đường cao kẻ từ A

D. Đường trung trực của BC

B. Phần tự luận (6 điểm)

Cho tam giác MNP có hai đường cao MQ và NH cắt nhau tại I. Biết (MIN) = 120^o

a. Tính (MPN)

b. Với góc P vừa tính được trong câu a và giả sử góc ∠M = 60^o. So sánh các cạnh của tam giác MNP

Đáp án và thang điểm

A. Phần trắc nghiệm (4 điểm)

Mỗi câu trả lời đúng được 1 điểm

1	2	3	4
B	D	A	A

Câu 1: Vì AI là tia phân giác của góc A nên ∠(BAI) = 90^o : 2 = 45^o. Chọn B

Câu 2: Chọn D

Câu 3: Trong tam giác BAH có ∠(BAH) + ∠(AHB) + ∠(ABH) = 180^o

⇒∠(BAH) = 180^o - 90^o - 50^o = 40^o

Chọn A

Câu 4: Chọn A

Quảng cáo

B. Phần tự luận (6 điểm)

a. Hình vẽ ( 1 điểm)

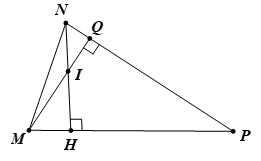
Do (MIN) là góc ngoài của tam giác MIH nên

∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)

⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120^o - 90^o = 30^o ( 1 điểm)

Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180^o

Nên ∠(MPQ) = 180^o - 30^o - 90^o = 60^o ( 1 điểm)

b. Với ∠(MPQ) = 60^o, ∠(NMP) = 60^o thì tam giác MNP cân tại N và có 1 góc bẳng 60^o nên tam giác ABC là tam giác đều ( 1 điểm)

Suy ra AB = BC = AC ( 1 điểm)

Phòng Giáo dục và Đào tạo .....

Đề kiểm tra 1 tiết Chương 3 Hình học

Môn: Toán lớp 7

Thời gian làm bài: 45 phút

(Trắc nghiệm)

Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:

Câu 1: Bất đẳng thức nào sau đây đúng trong tam giác.

A. AC + BC > AB > AC - BC

B. AC - BC > AB > AC + BC

C. AB - BC < AB < AC + BC

D. AC + BC = AB > AC - BC

Câu 2: Cho tam giác ABC cân tại A, BC = 10cm. Độ dài đường trung tuyến AM bằng 12cm. Khi đó độ dài AB là

A. 12cm B. 13cm C. 11cm D. 10cm

Câu 3: Cho tam giác ABC có ba cạnh là AB = 4cm, AC = 5cm, BC = 7cm. Khẳng định nào dưới đây là đúng?

A. ∠C < ∠B < ∠A B. ∠C < ∠A < ∠B

C. ∠B < ∠A < ∠C D. ∠A < ∠B < ∠C

Câu 4: Trực tâm của tam giác là:

A. Giao điểm của ba đường trung tuyến

B. Giao điểm của ba đường cao

C. Giao điểm của ba đường trung trực

D. Giao điểm của ba đường phân giác

Câu 5: Bộ ba đoạn thẳng nào sau đây tạo thành một tam giác

A. 2cm, 4cm, 5cm B. 2cm, 2cm, 4cm

C. 1cm, 2cm, 3cm D. 4cm, 4cm, 10cm

Câu 6: Cho tam giác ABC cân tại A, đường cao AH. Đường trung trực của cạnh AC cắt AH tại I. Chọn khẳng định đúng trong các khẳng định sau:

A. IA = IB = IC

B. Điểm I là trọng tâm tam giác ABC

C. Điểm I cách đều 3 cạnh của tam giác

D. Không có khẳng định nào đúng

Câu 7: Tam giác ABC có A là góc tù. Cạnh lớn nhất của tam giác ABC là

A. BC B. AC C. AB D. Không xác định

Câu 8: Trong tam giác ABC nếu AB = 6cm, AC = 15cm. Thì độ dài cạnh BC có thể là:

A. 10cm B. 9cm C. 8cm D. 7cm

Câu 9: Cho tam giác ABC có B > C Gọi AH là đường vuông góc kẻ từ điểm A đến đường thẳng BC. So sánh BH và HC

A. BH > HC B. BH = HC

C. BH < HC D. Không so sánh được

Câu 10: Một tam giác cân có độ dài hai cạnh là 4cm và 10cm. Tính chu vi của tam giác đó

A. 24cm B. 18cm C. 16cm D. 20cm

Câu 11: Cho tam giác ABC cân tại A, các đường trung tuyến BC và CE cắt nhau tại G. Chọn khẳng định đúng trong các khẳng định sau:

A. AG là tia phân giác của góc A của tam giác ABC

B. AG là đường trung trực của BC của tam giác ABC

C. AG là đường cao của tam giác ABC

D. Cả ba khẳng định đều đúng

Câu 12: Cho tam giác ABC có hai đường trung tuyến AE và BD cắt nhau tại G. Phát biểu nào sau đây là sai.

A. GA = GB B. GB = 2/3 BD

C. GE = 1/3 AE D. GA = 2GE

Câu 13: Cho tam giác ABC cân tại A. Trên BC lấy điểm H sao cho AH vuông góc với BC. Giữa AH lấy điểm Q. So sánh nào sau đây là sai.

A. QB < QH B. AB > QB

C. QB > BH D. QB = QC

Câu 14: Cho đoạn thẳng AB, tập hợp các điểm C sao cho tam giác ABC cân tại C là:

A. Đường trung trực của đoạn thẳng AB

B. Đường trung trực của AB trừ trung điểm M của AB

C. Tất cả các đường vuông góc với AB

D. Tất cả các đường song song với AB

Câu 15: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh độ dài AD, DC

A. AD > DC B. AD < DC

C. AD = DC D. Không so sánh được

Câu 16: Cho tam giác ABC vuông tại A. Trực tâm của tam giác ABC là điểm

A. Nằm bên trong tam giác

B. Nằm bên ngoài tam giác

C. Là trung điểm của cạnh huyền BC

D. Trùng với điểm A

Câu 17: Trên đường trung trực của đoạn thẳng AB, lấy hai điểm phân biệt M, N. Khi đó khẳng định nào sau đây đúng.

A. (AMN) ≠ (BMN) B. (MAN) ≠ (MBN)

C. (MNA) ≠ (MNB) D. ΔAMN = ΔBMN

Câu 18: Tam giác ABC có các đường phân giác BD và CE cắt nhau tại I trong đó góc BIC bằng 120^o. Số đo góc A là:

A.60^o B. 70^o C. 110^o D. 50^o

Câu 19: Cho tam giác MNP, E là trung điểm của NP, G là trọng tâm tam giác MNP và MG = 20cm. Độ dài đoạn GE là:

A. 15cm B. 40/3 cm C. 10cm D. 5cm

Câu 20: Cho tam giác ABC có AB < AC. Trên tia đối của tia BC lấy điểm D sao cho BD = BA, trên tia đối của tia CB lấy điểm E sao cho CE = CA. So sánh độ dài của AD và AE

A. AD < AE B. AD > AE

C. AD = AE D. Không so sánh được

Đáp án và thang điểm

Mỗi câu trả lời đúng được 0.5 điểm

1	2	3	4	5	6	7
A	B	A	B	A	A	A
8	9	10	11	12	13	14
A	C	A	D	A	A	B
15	16	17	18	19	20
B	D	D	A	C	A

Câu 1: Chọn A

Câu 2: Do tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao. BM=1/2 BC=5cm

Áp dụng định lí Pytago trong tam giác ABM ta có:

AB² = BC² + BM² = 12² + 5² = 169 ⇒ AB = 13cm. Chọn B

Câu 3: Vì AB < AC < BC ⇒ ∠C < ∠B < ∠A . Chọn A

Câu 4: Chọn B

Câu 5: Ta có 2 + 4 = 6 > 5 thỏa mãn bất đẳng thức tam giác. Chọn A

Câu 6: Chọn A

Câu 7: Chọn A

Câu 8: Theo BĐT tam giác có AC - AB < BC < AC + AB ⇒ 9 < BC < 21

Chọn A

Câu 9: Chọn C

Câu 10: Cạnh còn lại có thể bẳng 4cm hoặc 10cm, để thỏa mãn bất đẳng thức tam giác thì cạnh đó là 10cm.

Chu vi của tam giác là: 4 + 10 + 10=24. Chọn A

Câu 11: Chọn D

Câu 12: Chọn A

Câu 13: Chọn A

Câu 14: Chọn B

Câu 15: Chọn B

Câu 16: Chọn D

Câu 17: Chọn D

Câu 18: Trong tam giác BIC có ∠(BIC) + ∠(IBC) + ∠(ICB) = 180^o ⇒ (IBC) + (ICB) = 60^o

∠(ABC) + ∠(ACB) = 2∠(IBC) + 2∠(ICB) = 2(∠(IBC) + ∠(ICB) ) = 2.60^o = 120^o

Có ∠A = 180^o - 120^o = 60^o. Chọn A

Câu 19: Vì G là trọng tâm tam giác MNP nên GE = 1/2 MG = 10cm. Chọn C

Câu 20: Chọn A

Phòng Giáo dục và Đào tạo .....

Đề kiểm tra 1 tiết Chương 3 Hình học

Môn: Toán lớp 7

Thời gian làm bài: 45 phút

(Trắc nghiệm + Tự luận)

A. Phần trắc nghiệm (3 điểm)

Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:

Câu 1: Khẳng định nào sau đây đúng về giao điểm của ba đường phân giác của tam giác.

A. Cách đều ba cạnh của tam giác

B. Cách đều ba đỉnh của tam giác

C. Chia tam giác thành 2 phần có diện tích bằng nhau

D. Luôn nằm ngoài tam giác

Câu 2: Tam giác ABC có hai trung tuyến BM và CN cắt nhau tại trọng tâm G. Phát biểu nào sau đây là đúng

A. GM = GN B. GM = 1/3 GB

C. GN = 1/2 GC D. GB = GC

Câu 3: Cho tam giác ABC có AC > AB, đường cao AD. Trong các khẳng định sau khẳng định nào sai?

A. ∠(ABC) > ∠(ACB)

B. BD < DC

C. Hình chiếu của A lên BC là D

D. ∠(BAD) > ∠(DAC)

Câu 4: Cho tam giác vuông tại A có AB = 1cm, AC = 7cm. Biết độ dài cạnh BC là một số nguyên. BC là:

A. 6cm B. 8cm C. 7cm D. 9cm

Câu 5: Bộ ba nào sau đây không thể là ba cạnh của một tam giác

A. 3cm, 4cm, 5cm B. 6cm, 9cm, 12cm

C. 2cm, 4cm, 6cm D. 5cm, 8cm, 10cm

Câu 6: Cho tam giác MNP có M = 110^o, ∠N = 40^o. Cạnh nhỏ nhất của tam giác MNP là:

A. MN B. NP C. MP D. MN và NP

B. Phần tự luận (7 điểm)

Câu 1: (2 điểm) Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm

a. So sánh ba góc của tam giác ABC. Tam giác ABC là tam giác gì? Vì sao

b. Vẽ đường cao AH, lấy điểm M trên AH, so sánh MB và MC

Câu 2: (5 điểm) Cho tam giác ABC (AC > AB), trung tuyến AM. Trên tia đối của tia MA lấy D sao cho MD = MA

a. Chứng minh ΔMAB = ΔMDC rồi suy ra AB = CD

b. Chứng minh ∠(ADC) > ∠(DAC) . Từ đó suy ra ∠(MAB) > ∠(MAC) .

c. Kẻ đường cao AH. Lấy E là một điểm nằm giữa A và H. So sánh độ dài HC và HB, EB và EC.

Đáp án và thang điểm

A. Phần trắc nghiệm (3 điểm)

Mỗi câu trả lời đúng được 0.5 điểm

1	2	3	4	5	6
A	C	D	C	C	A

Câu 1: Chọn A

Câu 2: Chọn C

Câu 3: Chọn D

Câu 4: Ta có AC - AB < BC < AC + AB ⇒ 6 < BC < 8 ⇒ BC = 7cm.

Chọn C

Câu 5: Ta có: 2 + 4 = 6 ⇒ không thỏa mãn bất đẳng thức tam giác. Chọn C

Câu 6: Ta có: ∠P = 180^o - 110^o - 40^o = 30^o ⇒ P < N < M

⇒ NM < MP < MP

B. Phần tự luận (7 điểm)

Câu 1

a. Do BC > AC > AB ⇒ ∠A > ∠B > ∠C

Ta có AB² + AC² = 6² + 8² = 100 = 10² = BC²

Vậy tam giác ABC vuông tại A (1 điểm)

b. Do AB < AC ⇒ BH < HC ( Quan hệ giữa hình chiếu và đường xiên) (0.5 điểm)

Có MB và MC là hai đường xiên kẻ từ M

BH và HC lần lượt là hình chiếu của MB và MC

Mà BH < HC ⇒ MB < MC (0.5 điểm)

Câu 2

a. Hình vẽ (0.5 điểm)

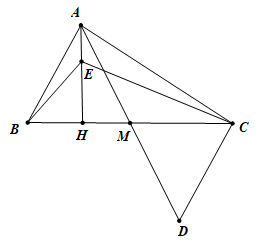
Xét ΔABM và ΔDCM có:

BM = MC

∠(AMB) = ∠(BMC)

AM = MD

⇒ ΔABM = ΔDCM (c.g.c) (0.5 điểm)

⇒ AB = DC (hai cạnh tương ứng) (0.5 điểm)

b. Theo câu a, AB = CD mà AB < AC ⇒ CD < AC (0.5 điểm)

Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (0.5 điểm)

Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM)

Suy ra (MAB) > (MAC) (0.5 điểm)

c. Vì AB < AC ⇒ HB < HC (quan hệ giữa hình chiếu và đường xiên) (1 điểm)

Vì HB < HC ⇒ BE < EC (quan hệ giữa hình chiếu và đường xiên) (1 điểm)

Xem thêm các Đề thi Toán 7 chọn lọc, có đáp án hay khác:

Lời giải bài tập lớp 7 sách mới:

ĐỀ THI, GIÁO ÁN, SÁCH LUYỆN THI DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 7

Bộ giáo án, bài giảng powerpoint, đề thi, sách dành cho giáo viên và khóa học dành cho phụ huynh tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

Tổng đài hỗ trợ đăng ký : 084 283 45 85

Giáo án, bài giảng powerpoint Văn, Toán, Lí, Hóa....

4.5 (243)

799,000đs

199,000 VNĐ

Đề thi, chuyên đề Cánh diều, Kết nối tri thức, Chân trời sáng tạo...

4.5 (243)

799,000đ

99,000 VNĐ

Sách Toán - Văn- Anh 6-7-8-9, luyện thi vào 10

4.5 (243)

199,000đ

99.000 - 149.000 VNĐ

xem tất cả

Loạt bài Đề thi Toán lớp 7 năm học 2023-2024 học kì 1, học kì 2 có đáp án của chúng tôi được biên soạn bám sát nội dung sgk Toán 7 giúp bạn giành điểm cao trong các bài thi Toán lớp 7.

Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.

Trang trước

Trang sau