Đề thi Giữa kì 1 Toán 12 năm 2024 có đáp án (30 đề)

Trọn bộ 30 đề thi Giữa kì 2 Toán 12 sách mới Chân trời sáng tạo, Kết nối tri thức, Cánh diều có đáp án và ma trận sẽ giúp bạn ôn tập và đạt điểm cao trong bài thi Toán 12.

Top 30 Đề thi Toán 12 Giữa kì 2 năm 2024 (có đáp án)

Xem thử Đề thi GK2 Toán 12 KNTT Xem thử Đề thi GK2 Toán 12 CTST Xem thử Đề thi GK2 Toán 12 CD

Chỉ từ 150k mua trọn bộ đề thi Toán 12 Giữa kì 2 bản word có lời giải chi tiết, dễ dàng chỉnh sửa:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

• Đề thi Giữa kì 2 Toán 12 Chân trời sáng tạo (có đáp án)

  Xem đề thi

• Đề thi Giữa kì 2 Toán 12 Kết nối tri thức (có đáp án)

  Xem đề thi

• Đề thi Giữa kì 2 Toán 12 Cánh diều (có đáp án)

  Xem đề thi

---

---

---

Lưu trữ: Đề thi Giữa kì 2 Toán 12 (sách cũ)

A. Ma trận 

1. Cấu trúc: 50 câu, mỗi câu 0,2 điểm

50 × 0,2 = 10 điểm.

2. Ma trận (số câu)

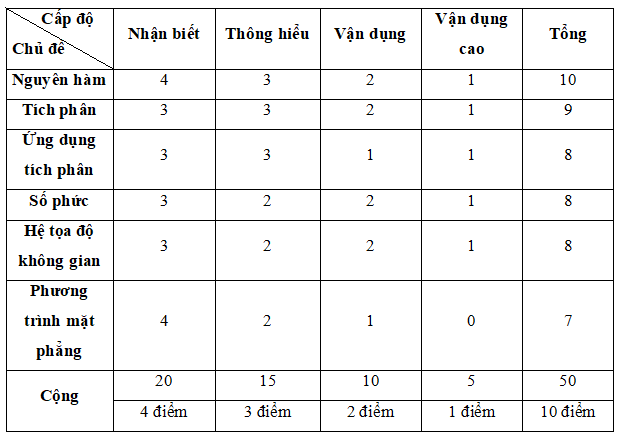
B. Đề bài

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 12

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

Câu 1: Trong không gian tọa độ Oxyz, cho mặt phẳng (α) có phương trình: x + y – z + 10 = 0. Tìm một điểm thuộc mặt phẳng (α) 

Câu 2: Trong không gian tọa độ Oxyz, tìm tọa độ hình chiếu vuông góc của điểm M(1;-2;9) lên mặt phẳng (Oxy).

Câu 3:  Chọn khẳng định sai trong các khẳng định dưới đây

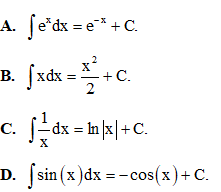
Câu 4: Cho f(x) liên tục trên đoạn [a; b] và có đạo hàm là F(x). Chọn khẳng định đúng trong các khẳng định dưới đây

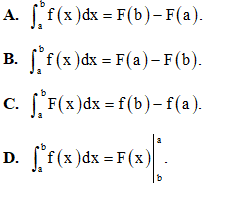
Câu 5: Trong không gian tọa độ Oxyz, cho hai vecto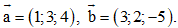

Tính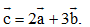

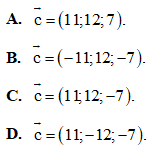
Câu 6: Tìm phần ảo của số phức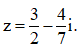

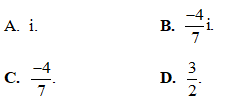
Câu 7: Trong không gian tọa độ Oxyz vớiba vecto đơn vị 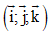,tính tọa độ vectơ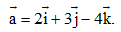 

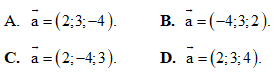
Câu 8: Nêu công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) (hàm y = f(x) liên tục trên [a; b]), trục Ox, đường thẳng x = a và đường thẳng x = b?

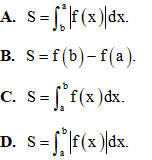
Câu 9:  Chọn khẳng định đúng trong các khẳng định dưới đây

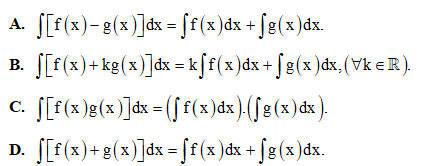
Câu 10: Tìm phần thực của số phức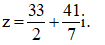

Câu 11: Trong không gian tọa độ Oxyz, cho ba điểm A(1; 1; 1), B(2; 4; 3), C (3; 7; m). Tìm m để ba điểm A, B, C thẳng hàng.

A. m = 4.                           B. m = 2.      

         

C. m = 5.                     D. m = 3.

Câu 12: Cho F(x) là một nguyên hàm của hàm f(x). Chọn khẳng định đúng trong các khẳng định dưới đây

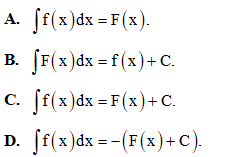
Câu 13: Trong các số phức bên dưới, tìm số thuần ảo.

A. z = 2021i.                   B. z = 3 – 4i.      

         

C. z = 2020 + 2021i.             D. z = 1 + 2i.

Câu 14: Tính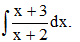

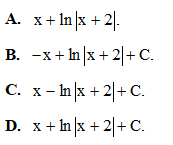
Câu 15:  Trong không gian tọa độ Oxyz, viết phương trình mặt phẳng đi qua điểm M(1;1;-2) và có vectơ pháp tuyến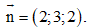

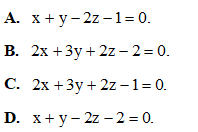
Câu 16:  Trong không gian tọa độ Oxyz, cho mặt phẳng (α) có phương trình: 4x + 6y - 2z - 7 = 0. Tìm một vectơ pháp tuyến của  mặt phẳng (α).

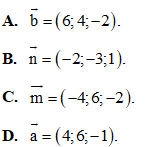
Câu 17: Tính diện tích hình phẳng giới hạn bởi các đường sau: y = x² – 2x, y = -x² + 4x, x = 0, x = 3.

A. 7.                       B. 9.  

                       

C. 6.                      D. 8.

Câu 18: Tính thể tích vật thể tròn xoay sinh ra bởi hình phẳng giới hạn bởi các đường sau khi quay quanh Ox: 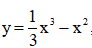,y = 0, x = 0, x = 3.

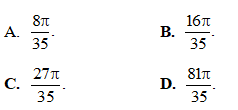
Câu 19: Tính diện tích hình phẳng giới hạn bởi các đường sau: y = x²– 2x, trục hoành, x = -1, x = 2.

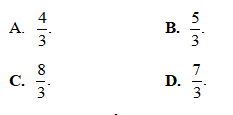
Câu 20:  Tính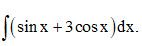 

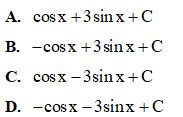
Câu 21: Trong không gian tọa độ Oxyz, cho hai điểm M(4; 3; 2), N(1; 2; 3). Tính tọa độ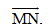

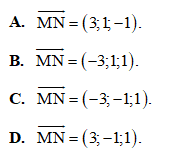
Câu 22: Chọn khẳng định sai trong các khẳng định dưới đây

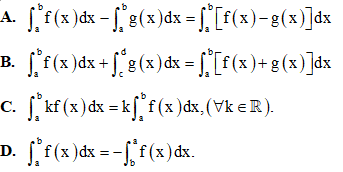
Câu 23:  Chọn khẳng định đúng trong các khẳng định dưới đây

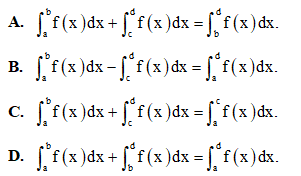
Câu 24: Điểm M trong hình ảnh bên dưới là điểm biểu diễn của số phức nào?

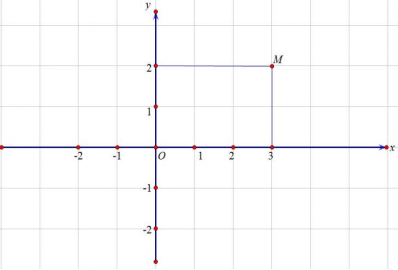
A. z = 2 + 3i.         B. z = 3 + 2i.        

         

C. z = 2i.             D. z = -3 + 2i.

Câu 25: Tính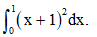

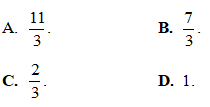
Câu 26: Tìm số phức liên hơp của số phức z = 4 + 5i.

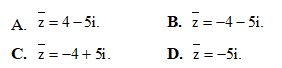
Câu 27:  Chọn khẳng định đúng trong các khẳng định dưới đây

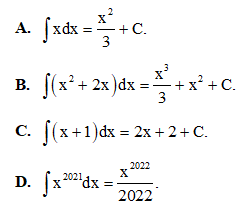
Câu 28: Tính độ dài của vecto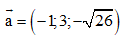

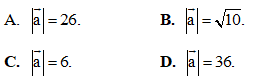
Câu 29:  Tìm F(x) là một nguyên hàm của hàm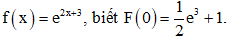

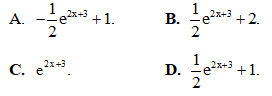
Câu 30: Nêu công thức tính thể tích khối tròn xoay được tạo thành khi quay miền D quay quanh trục hoành, biết D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) (hàm y = f(x) liên tục trên [a; b]), trục Ox, đường thẳng x = a và đường thẳng x = b?

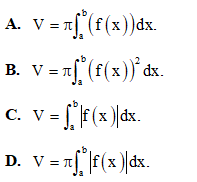
Câu 31: Trong không gian tọa độ Oxyz, phương trình mặt phẳng đi qua ba điểm A(1; 0; 0), B(0; 2; 0), C(0; 0; 3), là phương trình nào trong các phương trình dưới đây?

Câu 32: Tính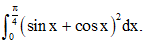

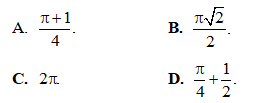
Câu 33: Tính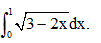

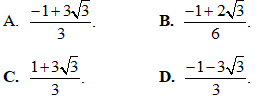
Câu 34: Biết D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) (hàm y = f(x)liên tục trên [a; b]), trục Ox, đường thẳng x = a và đường thẳng x = b (xem hình vẽ bên dưới). Tính diện tích của miền D?

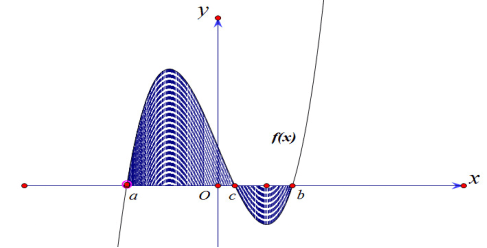
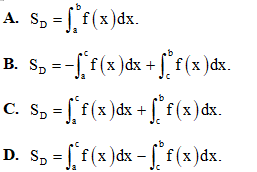
Câu 35: Trong không gian tọa độ Oxyz, phương trình mặt phẳng đi qua ba điểm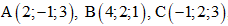 là phương trình nào trong các phương trình dưới đây?

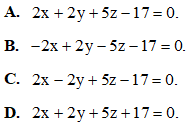
Câu 36: Cho số phức z = 5 – 4i. Số phức đối của z có điểm biểu diễn hình học là

A. (5; 4).                       B. (-5; -4).                    

C. (5; -4.)                  D. (-5; 4).

Câu 37: Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn 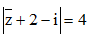 là đường tròn có tâm I và bán kính R lần lượt là :  

A.  I(-2; -1); R = 4.

B.  I(-2; -1); R = 2.

C.  I(2; -1); R = 4.

D.  I(2; -1); R = 2.

Câu 38: Cho 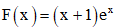là một nguyên hàm của hàm số 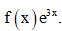Tìm nguyên hàm của hàm số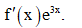

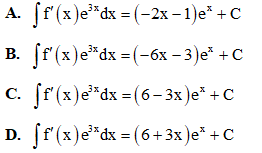
Câu 39: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 1; 1) và hai mặt phẳng (P): 2x - y + 3z - 1 = 0, (Q): y = 0. Viết phương trình mặt phẳng (R) chứa A, vuông góc với cả hai mặt phẳng (P) và (Q)?

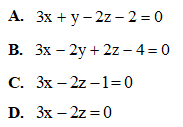
Câu 40: Trong không gian tọa độ Oxyz, viết phương trình mặt cầu có đường kính là A, B, biết A(0;1;-3), B(4;3;1).

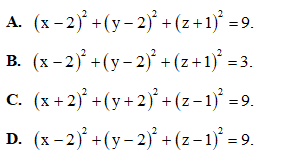
Câu 41: Cho hàm số 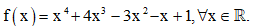Tính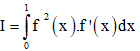 

Câu 42: Cho tích phân 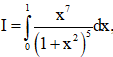giả sử đặt t = 1 + x² Tìm mệnh đề đúng?

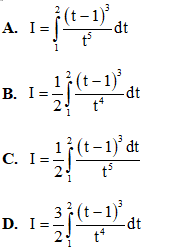
Câu 43: Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = -x² + 2x + 1 và y = 2x² - 4x + 1 là

A.  6.                     B.  7.                       

C.  5.                    D.  4.

Câu 44: Tìm họ nguyên hàm của hàm số f(x) = tan⁵x

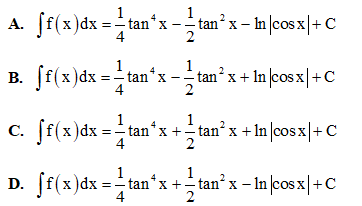
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho các điểm 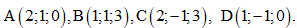 Bán kính mặt cầu ngoại tiếp tứ diện ABCD là

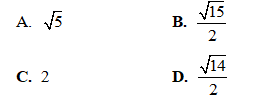
Câu 46: Phương trình đường thẳng song song với đường thẳng 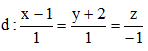và cắt hai đường thẳng  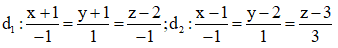là

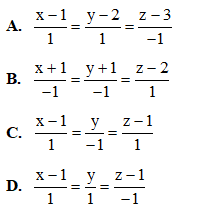
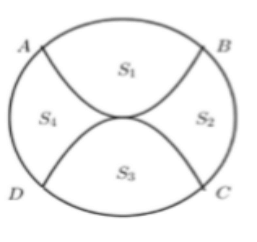
Câu 47:  Cho hàm số y = f(x) có f'(x) liên tục trên nửa khoảng [0; +∞) thỏa mãn 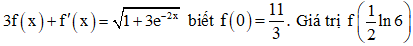bằng

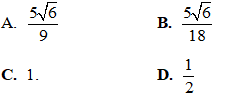
Câu 48:  Khuôn viên trường THPT Hòa Bình có một bồn hoa hình tròn có tâm O. Một nhóm học Sinh 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích S₁, S₂ dùng để trồng hoa, phần diện tích S₃, S₄ dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là 150 000 đồng/ 1 m²,   kinh phí trồng cỏ là 100 000 đồng/1 m². Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn). 

A.  6 060 000 đồng

B.  3 270 000 đồng   

C.  3 000 000 đồng

D.  5 790 000 đồng

Câu 49:  Cho hàm số y = f(x) xác định trên 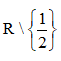thỏa mãn điều kiện  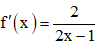f(0) = 1, f(1) = 2. Giá trị của biểu thức f(-1) + f(3) bằng

A. 3 + ln15                       B. 4 + ln15                    

C. 2 + ln15          D. ln15

Câu 50:  Cho số phức z thỏa mãn |z – 1 – i| = 1, số phức w thỏa mãn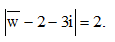  Tính giá trị nhỏ nhất của |z – w|.

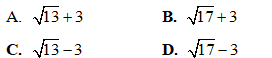
--- HẾT ---

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 12

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

Câu 1. Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng 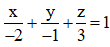 là

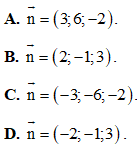
Câu 2. Cho hàm số y = f(x) có đạo hàm 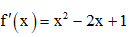. Khẳng định nào sau đây đúng?

A.Hàm số nghịch biến trên (-∞; 1) ∪ (1; +∞).

B.Hàm số nghịch biến trên (-∞; +∞).

C. Hàm số nghịch biến trên (-1;1).

D.Hàm số đồng biến trên (-∞; +∞).

Câu 3. Cho khối nón có độ dài đường sinh bằng đường kính đáy bằng a. Thể tích khối nón là.

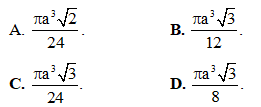
Câu 4. Cho hàm số f(x) có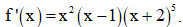 Số điểm cực trị của hàm số đã cho là

A. 1.                       B. 2.  

               

C. 3.                    D. 4.

Câu 5. Trong các khẳng định sau, khẳng định nào sai?

A. Nếu giá của ba vectơ 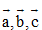cắt nhau từng đôi một thì ba vectơ đó đồng phẳng.

B. Nếu trong ba vectơ 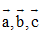có một vectơ  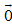thì ba vectơ đó đồng phẳng.

C. Nếu giá của ba vectơ 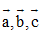 cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.

D. Nếu trong ba vectơ 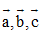 có hai vectơ cùng phương thì ba vectơ đó đồng phẳng.

Câu 6. Cho đồ thị(C) của  hàm số y = f(x) có bảng biến thiên                    

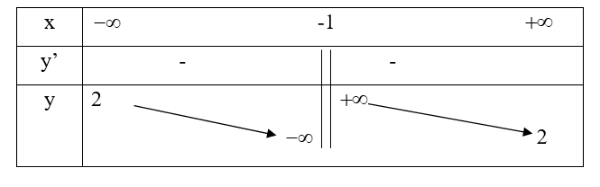
Đồ thị (C) của hàm số có bao nhiêu đường tiệm cận.

A. 2.                     B. 1.    

                 

C. 0.                     D. 3.

Câu 7. Đặt 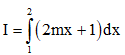 (m là tham số thực). Tìm m để I = 4.

A. m = -1.                   B. m = 1.    

           

C. m = -2.                D. m = 2.

Câu 8. Hàm số nào sau đây có đồ thị  như hình vẽ bên?

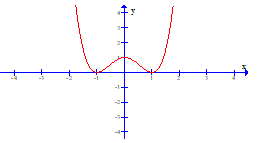
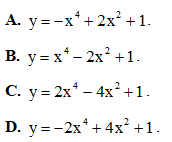
Câu 9. Đặt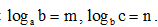 Khi đó 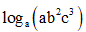bằng

A. 1 + 6mn.                   B.1 + 2m + 3n.            

         

C. 6mn.                D. 1 + 2m + 3mn.

Câu 10. Cho hàm số y = f(x) xác định và liên tục trên  và có bảng biến thiên

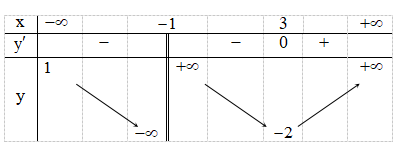
Khẳng định nào sau đây sai?

A. Hàm số nghịch biến trên khoảng (-∞; 3).

B. Giá trị nhỏ nhất của hàm số trên đoạn [1; 8] bằng -2.

C. Hàm số đạt cực tiểu tại x = 3.

D. Phương trình f(x) = m có 3 nghiệm thực phân biệt khi m ∈(-2;1).

Câu 11.Cho đồ thị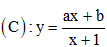 như hình dưới.

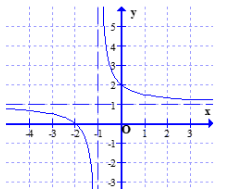
Mệnh đề nào sau đây đúng?

A. b > 0 > a.                     B. b > a > 0.        

         

C. a > b > 0.                  D. a > 0 > b.

Câu 12. Thể tích của một khối hộp chữ nhật có các cạnh 1cm, 2cm, 3cm là

A. 3cm³.                    B. 2cm³.      

         

C. 6cm³.                    D. 12cm³.

Câu 13. Biết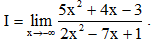Giá trị của I bằng

.

Câu 14. Tìm tất cả các giá trị thực của tham số m để hàm số 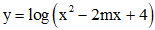có tập xác định là R.

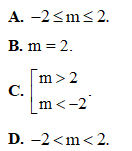
Câu 15. Cho các mệnh đề sau:

1) Nếu hàm số y = f(x) liên tục, có đạo hàm tới cấp hai trên (a; b); x₀ ∈ (a;b) và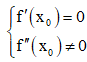 thì x₀ là một điểm cực trị của hàm số.

2) Nếu hàm số y = f(x) xác định trên [a; b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

3) Nếu hàm số y = f(x) liên tục trên [a; b] thì hàm số có đạo hàm tại mọi x thuộc [a; b].

4) Nếu hàm số y = f(x) có đạo hàm trên [a; b] thì hàm số có nguyên hàm trên [a; b].

Số mệnh đề đúng là

A. 4.                   B. 2.    

               

C. 1.                  D. 3.

Câu 16. Phương trình 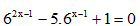có hai nghiệm x₁, x₂. Khi đó tổng hai nghiệm x₁ + x₂ là.

A. 5.                  B. 3.    

               

C. 2.                  D. 1.

Câu 17. Tính thể tích của phần vật thể tạo nên khi quay quanh trục Ox hình phẳng D giới hạn bởi đồ thị (P): y = 2x - x² và trục Ox bằng

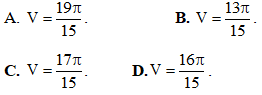
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1;5;3) và M(2;1;-2). Tọa độ điểm B biết M là trung điểm của đoạn AB là

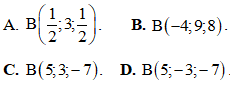
Câu 19. Tập nghiệm của bất phương trình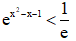  là.

Câu 20. Nguyên hàm của hàm số f(x) = 2^x + x là

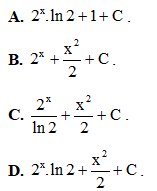
Câu 21. Với k, n là số nguyên dương 1 ≤ k ≤ n. Đẳng thức nào sau đây là đúng

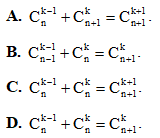
Câu 22. Cho hình chóp tam giác đều có tất cả các cạnh bằng a. Thể tích khối chóp là

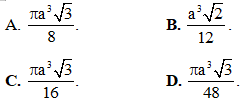
Câu 23. Cho hàm số y = f(x) có đạo hàm trên R, và đồ thị của hàm số y = f'(x) như hình dưới đây. Số điểm cực đại của hàm số y = f(x) là

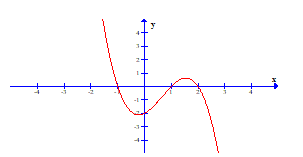
A. 0.                  B. 2.          

       

C. 1.                   D. 3.

Câu 24. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 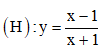 và các trục tọa độ. Khi đó giá trị của S bằng

A. S = ln2 + 1.          B. S = 2ln2 + 1.

C. S = ln2 – 1.       D. S = 2ln2 – 1. 

Câu 25. Hiệu của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = 2x – lnx trên đoạn 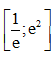là

Câu 26. Một vật chuyển động có phương trình 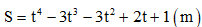, t là thời gian tính bằng giây. Gia tốc của vật tại thời điểm t = 3s là

A. 48m/s²                 B.  28m/s²                  

C. 18m/s²                  D. 54m/s²

Câu 27. Người ta chế tạo một thiết bị hình trụ như hình vẽ dưới. 

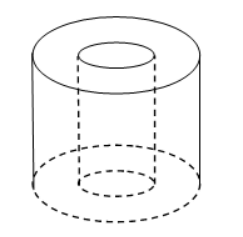
Biết hình trụ nhỏ phía trong và hình trụ lớn phía ngoài có chiều cao bằng nhau và có bán kính lần lượt là  r₁, r₂ thỏa mãn r₂ = 3r₁. Tỉ số thể tích của phần nằm giữa hai hình trụ và hình trụ nhỏ là.

A. 4.                   B. 6.      

           

C. 9.                   D. 8.

Câu 28. Tính tích phân 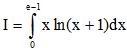ta được kết quả có dạng 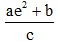, trong đó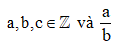là phân số tối giản. Tính T = a² + 2b - 3c

A. 17.                   B. 10.        

         

C. -17.                   D. 18.

Câu 29. Diện tích của một mặt cầu bằng 16π(cm²). Bán kính của mặt cầu đó là

A. 8 cm.              B. 2 cm.  

             

C. 4 cm.                  D. 6 cm.

Câu 30.Trong không gian với hệ toạ độ Oxyz, cho ba điểm 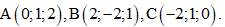Khi đó, phương trình mặt phẳng (ABC) là ax + y – z + d = 0. Hãy xác định a và d.

A. a = 1, d = 1.

B. a = 6, d = -6.

C. a = -1, d = -6.

D. a = -6, d = 6.

Câu 31.Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và 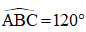. Góc giữa cạnh bên AA' và mặt đáy bằng 60°. Đỉnh A' cách đều các điểm A, B, D. Tính theo a thể tích V của khối lăng trụ đã cho.

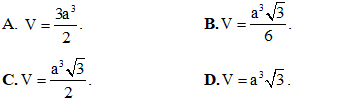
Câu 32.Trong hệ tọa độ Oxyz cho I(1; 1; 1) và mặt phẳng (P): 2x + y + 2z + 4 = 0. Mặt cầu (S) tâm I cắt (P) theo một đường tròn bán kính r = 4. Phương trình của (S) là

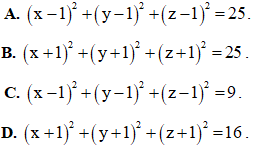
Câu 33. Cho đồ thị hàm số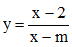. Tìm các giá trị của tham số m để hàm số đồng biến trên (0; 3].

A. m > 3.             B. 0 < m < 2      

           

C. 2 < m ≤ 3.            D. m ≤ 0.

Câu 34. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(2; 1; 3), B(1; -1; 2), C(3; -6; 1). Điểm M(x; y; z) thuộc mặt phẳng (Oyz) sao cho MA² + MB² + MC² đạt giá trị nhỏ nhất. Tính giá trị của biểu thức P = x + y + z.

A. P = 0.             B. P = 2.      

                   

C. P = 6.                   D. P = -2.

Câu 35. Cho hàm số 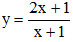 có đồ thị (C). Gọi S tà tập tất các giá trị của tham số m để đường thẳng d: y = x + m – 1 cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho AB = 2√3. Tính tổng bình phương các phần tử của S.

A. 38.                 B. 52.

                               

C. 28.                       D. 14.

Câu 36. Cho phương trình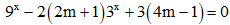 có 2 nghiệm thực x₁, x₂ thỏa mãn (x₁ + 2)(x₂ + 2) = 12. Giá trị của m thuộc khoảng 

A. (9; +∞)                  B. (3; 9)        

         

C. (-2; 0)                  D. (1; 3)

Câu 37. Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau

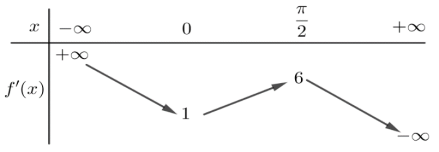
Bất phương trình 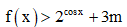đúng với mọi  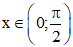khi và chỉ khi

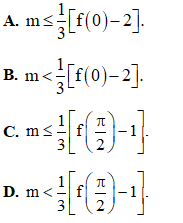
Câu 38. Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp hộp. Gọi h là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết 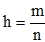 với m, n là các số nguyên dương nguyên tố cùng nhau. Tổng m + n là

A. 12.                     B. 13    

             

C. 11.                     D. 10.

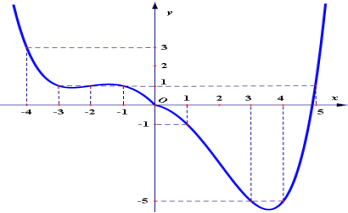
Câu 39. Cho hàm số y = f(x) xác định, liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình 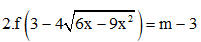 có nghiệm.

A. 13.                  B. 12.    

                 

C. 8.                   D. 10.

Câu 40. Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau

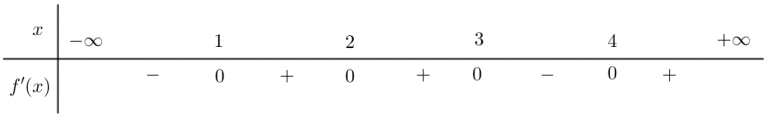
Hàm số 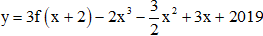 đồng biến trên khoảng nào dưới đây?

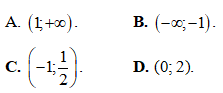
Câu 41. Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng (xem hình minh họa). 

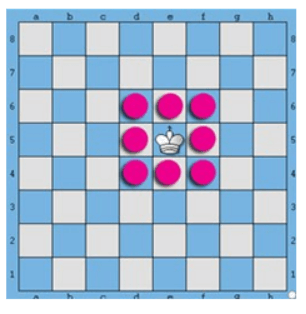
Bạn An di chuyển quân vua ngẫu nhiên 3 bước. Xác suất để sau 3 bước đi quân vua trở về ô xuất phát là 

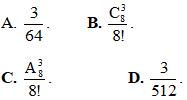
Câu 42. Trong không gian với hệ tọa độ Oxyz, cho điểm A(a; b; c) với x, y, z là các số thực dương thỏa mãn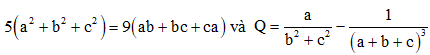có giá trị lớn nhất. Gọi M, N, P lần lượt là hình chiếu vuông góc của A lên các tia Ox, Oy, Oz. Phương trình mặt phẳng (MNP) là

A. x + 4y + 4z – 12 = 0.

B. 3x + 12y + 12z – 1 = 0.

C. x + 4y + 4z = 0.

D. 3x + 12y + 12z + 1 = 0.

Câu 43.Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình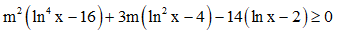đúng với mọi x ∈ (0; +∞). Tổng giá trị của tất cả các phần tử thuộc S bằng:

Câu 44. Anh C đi làm với mức lương khởi điểm là x (triệu đồng)/tháng, và số tiền lương này được nhận vào ngày đầu tháng. Vì làm việc chăm chỉ và có trách nhiệm nên sau 36 tháng kể từ ngày đi làm, anh C được tăng lương thêm 10%. Mỗi tháng, anh ta giữ lại 20% số tiền lương để gửi tiết kiệm vào ngân hàng với kì hạn 1 tháng và lãi suất là 0,5%/tháng, theo hình thức lãi kép (tức là tiền lãi của tháng này được nhập vào vốn để tính lãi cho tháng tiếp theo). Sau 48 tháng kể từ ngày đi làm, anh C nhận được số tiền cả gốc và lãi là 100 triệu đồng. Hỏi mức lương khởi điểm của người đó là bao nhiêu?

A. 8 991 504đồng.

B. 9 891 504 đồng.

C. 8 981 504đồng.

D. 9 881 505 đồng.

Câu 45. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng song song (P): 2x – y + 2z – 1 = 0, (Q): 2x – y + 2z + 5 = 0 và điểm A(– 1; 1; 1) nằm trong khoảng giữa hai mặt phẳng này. Gọi (S) là mặt cầu đi qua A và tiếp xúc với cả (P) và (Q). Biết khi (S) thay đổi thì tâm I của nó luôn thuộc một đường tròn (C) cố định. Diện tích hình tròn giới hạn bởi (C) là 

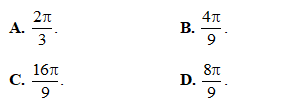
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết rằng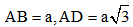 và 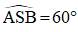. Tính diện tích của khối cầu ngoại tiếp hình chóp S.ABCD.

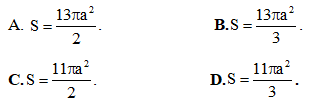
Câu 47. Cho hàm số y = f(x) có đạo hàm liên tục trên R. Hàm số y = f'(x) có đồ thị như hình vẽ bên dưới:

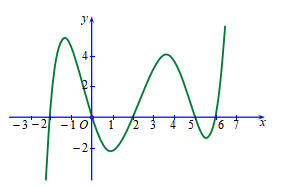
Số nghiệm thuộc đoạn [-2; 6] của phương trình f(x) = f(0) là

A. 5.                        B. 2.                        C. 3.                      D. 4.

Câu 48. Một mặt bàn hình elip có chiều dài là 120 cm, chiều rộng là là 60 cm. Anh Hải muốn gắn đá hoa cương cho mặt bàn theo hình (phần đá hoa cương trắng và phần đá hoa cương màu vàng), biết rằng phần màu vàng cũng là elip có chiều dài 100 cm và chiều rộng là 40 cm. Biết rằng đá hoa cương màu trắng có giá 600 000 vnđ/m²  và đá hoa cương màu vàng có giá 650 000 vnđ/m². Hỏi số tiền để gắn đá hoa cương theo cách trên gần nhất với số tiền nào dưới đây?

A. 355 000đồng.

B. 339 000đồng.

C. 368 000đồng.

D. 353 000đồng

Câu 49. Cho lăng trụ ABC.A'B'C' có thể tích bằng 2. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AA' và BB' sao cho M là trung điểm của AA' và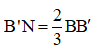 . Đường thẳng CM cắt đường thẳng C'A' tại P và đường thẳng CN cắt đường thẳng C'B' tại Q. Thể tích khối đa diện lồi A'MPB'NQ bằng

Câu 50. Cho hàm số f(x) thỏa mãn 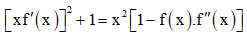với mọi x dương. Biết f(1) = f'(1) = 1. Giá trị f²(2) bằng

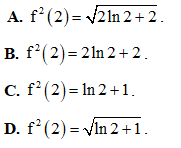
--- HẾT ----

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 12

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

Câu 1: Cho hàm số y = f(x) liên tục trên đoạn [a ; b] , hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x) ; trục hoành và hai đường thẳng x = a ; x = b . Gọi  V  là thể tích khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục hoành. Chọn khẳng định đúng trong các khẳng định sau:

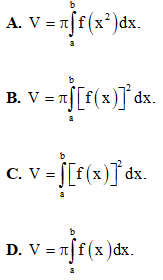
Câu 2: Trong các công thức sau, công thức nào sai?

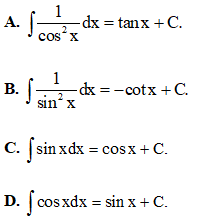
Câu 3: Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a ; b]. Trong các đẳng thức sau , đẳng thức nào sai?

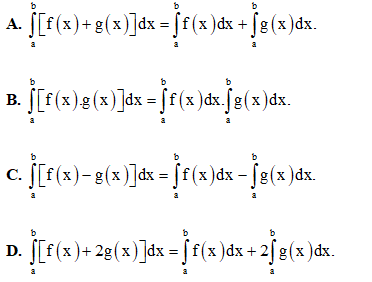
Câu 4: Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a ; b] , hình phẳng (H) giới hạn bởi đồ thị hai hàm số trên và hai đường thẳng x = a ; x = b. Gọi S là diện tích hình phẳng (H). Chọn khẳng định đúng trong các khẳng định sau:

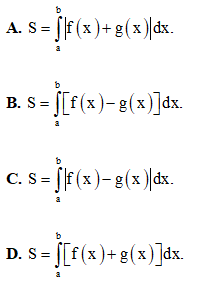
Câu 5: Cho hàm số y = f(x) liên tục trên R. Trong các đẳng thức sau , đẳng thức nào sai?

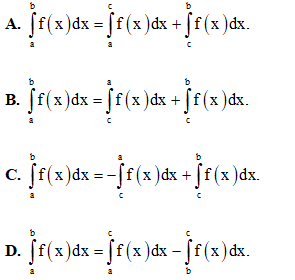
Câu 6: Trong các công thức sau, công thức nào sai?

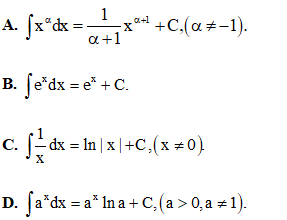
Câu 7: Tìm nguyên hàm của hàm số f(x) = e^3x

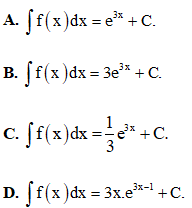
Câu 8: Tính tích phân: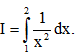

Câu 9: Tính tích phân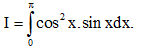

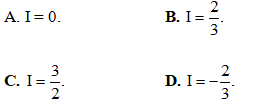
Câu 10: Tìm nguyên hàm của hàm số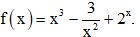

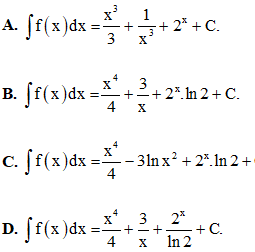
Câu 11: Biết 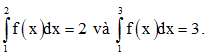Tính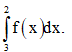 

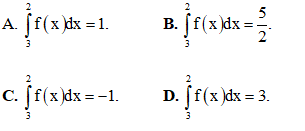
Câu 12: Tính diện tích S của hình phẳng giới hạn bởi đường cong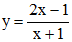; y = 0 và x = 0; x = 1.

Câu 13: Tính 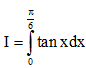là :

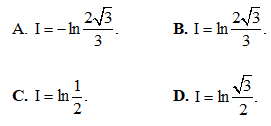
Câu 14: Tính thể tích V của vật thể tròn xoay sinh ra bởi hình phẳng (H) quay quanh trục Ox, biết (H) giới hạn bởi các đường: y = lnx, y = 0, x = e.

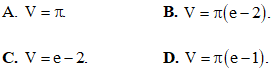
Câu 15: Cho F(x) là 1 nguyên hàm của f(x) trên 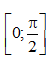, biết 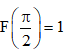và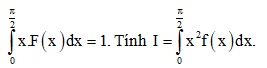  

Câu 16: Người ta trồng hoa tại phần đất nằm phía ngoài đường tròn bán kính bằng 2(m) và phía trong của elip, biết elip có tâm trùng với tâm của đường tròn và độ dài trục lớn là 10(m), độ dài trục nhỏ là 6(m). Trong mỗi mét vuông cần bón 1,3 kg phân hữu cơ. Cửa hàng bán phân hữu cơ chỉ bán bao phân hữu cơ, mỗi bao 10kg (không bán lẻ từng kg phân hữu cơ). Cần mua ít nhất mấy bao phân hữu cơ để bón cho hoa?

A. 6 bao.                   B. 3bao.  

                 

C. 4 bao.                    D. 5 bao.

Câu 17: Cho hàm số f(x) liên tục trên đoạn [0; 1], biết 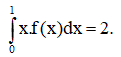Tính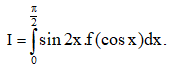 

A. I = 1.                   B. I = 8.    

           

C. I = 4.                    D. I = 6.

Câu 18: Hình phẳng (H) giới hạn bởi trục hoành và đồ thị hai hàm số y = -x + 2; y = x², (x ≥ 0) Tính diện tích S của hình phẳng (H).

Câu 19: Cho số phức z = a + bi với a,b là số thực. Tìm 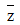 là số phức liên hợp của số phức z .

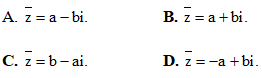
Câu 20: Cho số phức khác không z = a + bi với a,b là số thực. Tìm 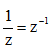 là số phức nghịch đảo của số phức z .

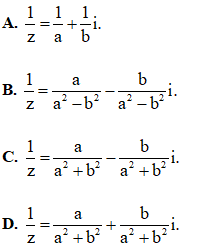
Câu 21: Cho số phức z = a + bi với a, b là số thực. Tìm điểm M biểu diễn số phức z trong mặt phẳng tọa độ Oxy.

A. M(a ; -b).              B. M(-a ; b).

               

C. M(a ; b).               D. M(b ; a).

Câu 22: Cho số phức z = a + bi với a,b là số thực. Tìm |z| là mô-đun của số phức z .

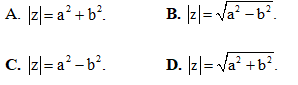
Câu 23: Cho số phức z = a + bi (a,b ∈ R) thỏa mãn (1 + 2i)z = 3 - i. Tính T = a – b.

Câu 24: Cho số phức 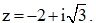Tính môđun của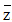

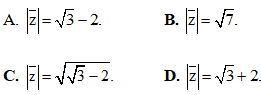
Câu 25: Cho số phức z thỏa mãn (2 - )z = 7 - i. Tìm điểm M là điểm biểu diễn số phức  trên mặt phẳng tọa độ.

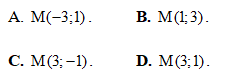
Câu 26: Cho hai số thực x, y thỏa: 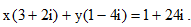 Tính  S = x + 2y .

A. S = -8                   B. S = 12        

                 

C. S = -3                   D. S = 3

Câu 27: Cho 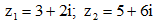. Tìm phần thực và phần ảo của số phức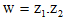

A. 3 và 28.                      B. 5 và -5.                     C. 3 và -5.                   D. 3 và -5.

Câu 28: Trong mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn 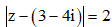 là

A. Đường tròn tâm I(3; 4), bán kính bằng 4.

B. Đường tròn tâm I(3; 4), bán kính bằng 2.

C. Đường tròn tâm I(-3;- 4),bán kính bằng 4.

D. Đường tròn tâm I(3; -4), bán kính bằng 2.

Câu 29: Cho 2 số phức z₁, z₂ thỏa mãn 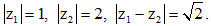Tính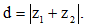 

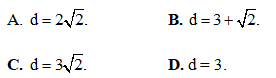
Câu 30: Gọi z₁, z₂ là hai nghiệm của phương trình z² - 3z + 5 = 0. Tính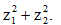

A. -19.                      B. –1.      

               

C. 1.                        D. 19.

Câu 31: Trong không gian Oxyz , cho 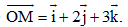 Tìm tọa độ điểm M .

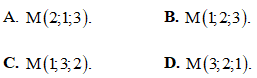
Câu 32: Trong không gian Oxyz , cho mặt phẳng (P) qua điểm M(a; b; c) và mặt phẳng (P) có một véc tơ pháp tuyến là 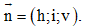 Tìm phương trình của mặt phẳng (P).

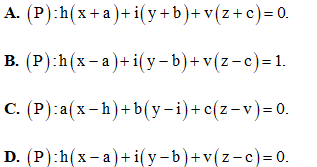
Câu 33: Trong không gian Oxyz , cho mặt cầu (S) có tâm I(a; b; c) và bán kính là R. Tìm phương trình của mặt cầu (S).

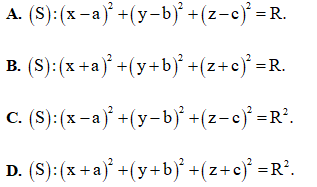
Câu 34: Trong không gian Oxyz , cho đường thẳng d qua 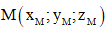và đường thẳng d có một véc tơ chỉ phương là  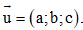Tìm phương trình tham số của đường thẳng d.

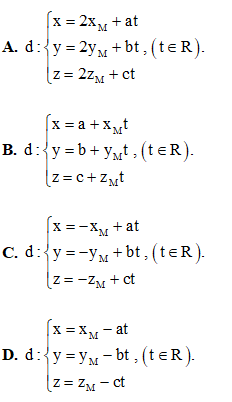
Câu 35: Trong không gian Oxyz, cho hai vectơ 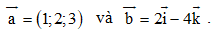Tính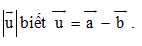

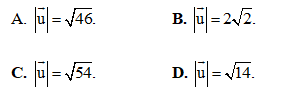
Câu 36: Trong không gian Oxyz, cho điểm A(2;-6;4). Tìm phương trình mặt cầu (S) có đường kính 

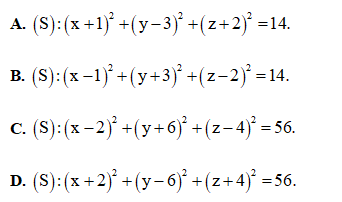
Câu 37: Trong không gian Oxyz, cho ba điểm A(3; -1 ; 2) , B(4 ; -1 ; -1), C(2 ; 0 ; 2).   Mặt phẳng (P) đi qua ba điểm A, B, C có phương trình là:

A. (P): 2x + 3y – z + 8 = 0.

B. (P): 3x – 3y + z – 14 = 0.

C. (P): 3x – 2y + z – 8 = 0.

D. (P): 3x + 3y + z – 8 = 0.

Câu 38: Trong không gian Oxyz, cho điểm M(2;-1;3). Tìm phương trình mặt phẳng (P) chứa trục  và mặt phẳng (P) qua điểm .

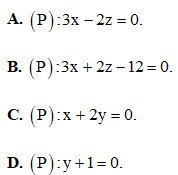
Câu 39: Trong không gian Oxyz, cho mặt cầu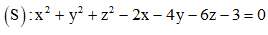và mặt phẳng 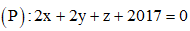, đường thẳng  đi qua tâm mặt cầu và vuông góc với mặt phẳng Tìm phương trình chính tắc của đường thẳng .

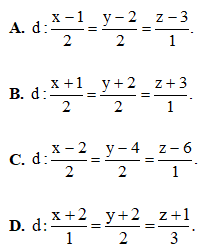
Câu 40: Trong không gian Oxyz, cho hai mặt phẳng song song 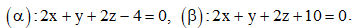Tính khoảng cách h giữa hai mặt phẳng (α) và (β)

A. h  =  6.                  B. h  = 14.

                   

C. h  =  2.                  D. h  = 14/3 .

Câu 41: Trong không gian Oxyz, cho điểm A(2; 3; 1) và đường thẳng 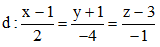. Viết phương trình đường thẳng ∆ đi qua A và đường thẳng ∆ song song với đường thẳng d.

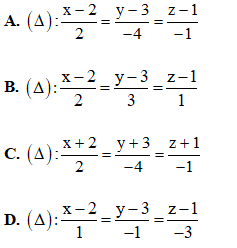
Câu 42: Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;3;-1) và mặt phẳng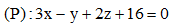 Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S).

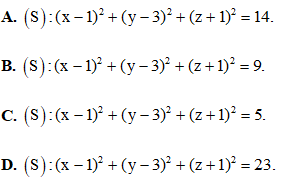
Câu 43: Cho khối nón có chiều cao h = 4a và độ dài đường sinh l = 5a. Tìm thể tích V của khối nón.

Câu 44: Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng 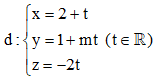và mặt cầu  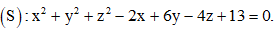Có bao nhiêu giá trị nguyên của tham số m để d cắt (S) tại hai điểm phân biệt?

A. 5                     B. 3  

                     

C. 2                     D. 1

Câu 45: Cho hai điểm A, B thuộc mặt cầu và AB = 8 cm, biết khoảng cách từ tâm mặt cầu đến đường thẳng AB là 3 cm. Tính thể tích V của khối cầu.

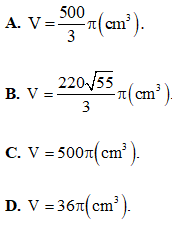
Câu 46: Tính tích phân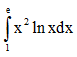

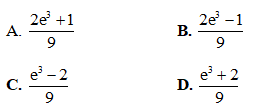
Câu 47: Gọi h(t) (cm) là mức nước ở một bồn chứa sau khi bơm nước vào bồn được t giây. Biết rằng 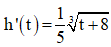 và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 56 giây.

A. 38,4 cm                B. 51,2 cm

                 

C. 36 cm                  D. 40,8 cm

Câu 48: Xét hàm số 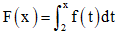 trong đó hàm số y = f(t) có đồ thị như hình vẽ bên.

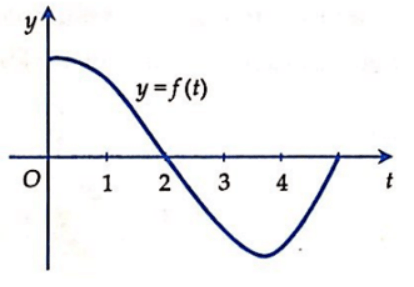
Giá trị nào dưới đây là lớn nhất?

A. F(0)                       B. F(1)  

                       

C. F(2)                         D. F(3) 

Câu 49: Cho hình phẳng D giới hạn bởi đồ thị các hàm số 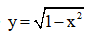và y = 2(1 – x). Biết thể tích khối tròn xoay dc tạo thành khi quay D quanh trục Ox bằng 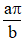, trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm a – b.

A. 71                     B. ‒71    

                   

C. 2                     D. ‒2

Câu 50: Biết 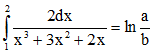, trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm a + b.

A. 59                       B. 58    

                     

C. 57                       D. 56

--- HẾT ----

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 12

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 4)

Câu 1. Biết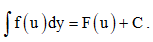Mệnh đề nào dưới đây đúng?

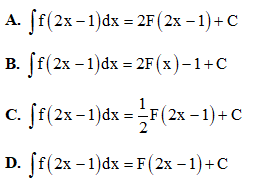
Câu 2. Cho hai mặt phẳng (P): x + my + (m – 1)z + 1 = 0 và (Q): x + y + 2z = 0. Tập hợp tất cả các giá trị của m để hai mặt phẳng này không song song là:

A. (0; +∞)                   B. R \ {– 1; 1; 2}                    

C. (–∞;  –3)                D. R

Câu 3. Giả sử 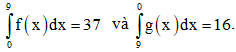. Khi đó  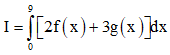 bằng:

A. I = 122                    B. I = 26                                

C. I = 143                    D. I = 58

Câu 4. Trong không gian Oxyz, cho ba điểm A(1; – 2; 3), B(4; 2; 3), C(3; 4; 3). Gọi (S₁), (S₂), (S₃) là các mặt cầu có tâm A, B, C và bán kính lần lượt bằng 3, 2, 3. Hỏi có bao nhiêu mặt phẳng qua điểm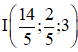 và tiếp xúc với cả 3 mặt cầu (S₁), (S₂), (S₃).

A. 2                      B. 7                     

C. 0                      D. 1

Câu 5. Cho 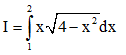và đặt  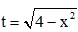. Khẳng định nào sau đây sai?

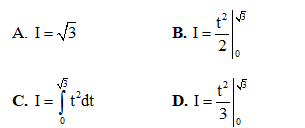
Câu 6. Cho (H) là hình phẳng giới hạn bởi đường cong có phương trình 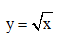, nửa đường tròn có phương trình 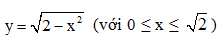và trục hoành (phần tô đậm trong hình vẽ).

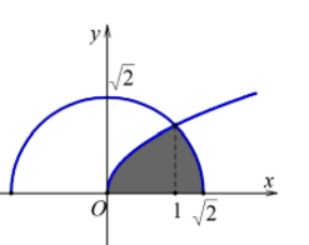
Diện tích của hình (H)  bằng:

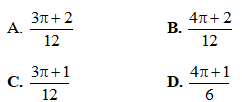
Câu 7. Tìm nguyên hàm của hàm số f(x) =xe^x.

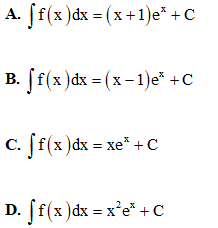
Câu 8.  Biết rằng tích phân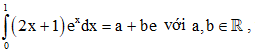, tích ab bằng:

A. 1                          B. –1                    

C. –15                   D. 20

Câu 9. Trong không gian với hệ tọa độ Oxyz, cho H(1; 2; 3). Viết phương trình mặt phẳng (P) đi qua điểm H và cắt các trục tọa độ tại ba điểm phân biệt A, B, C sao cho H là trực tâm tam giác ABC.

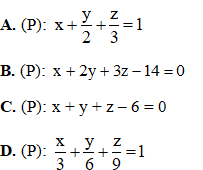
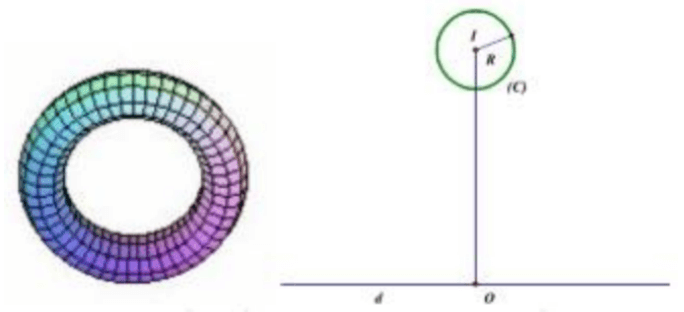
Câu 10. Người ta làm một chiếc phao như hình vẽ (với bề mặt có được bằng cách quay đường tròn (C) quanh trục d). Biết OI = 30 cm, R = 5 cm. Tính thể tích V của chiếc phao.

A. V = 1500π² cm³

B. V = 900π² cm³

C. V = 1500π cm³

D. V = 900π cm³

Câu 11. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; -2; 3) và B(5; 4; 7). Phương trình mặt cầu nhận AB làm đường kính là:

A. (x – 6)² + (y – 2)² + (z – 10)² = 17  

B. (x – 1)² + (y + 2)² + (z – 3)² = 17 

C. (x – 3)² + (y – 1)² + (z – 5)² = 17 

D. (x – 5)² + (y – 4)² + (z – 7)² = 17

Câu 12. Tích phân 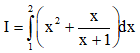 có giá trị là :

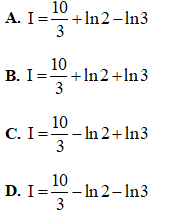
Câu 13. Trong không gian Oxyz, cho hai mặt phẳng (P): x – y – z + 6 = 0; (Q): 2x + 3y – 2z + 1 = 0. Gọi (S) là mặt cầu có tâm thuộc (Q) và cắt (P) theo giao tuyến là đường tròn có tâm E(-1; 2; 3), bán kính r = 8. Phương trình mặt cầu (S) là:

A. x² + (y + 1)² + (z + 2)² = 64

B. x² + (y – 1)² + (z – 2)² = 67

C. x² + (y – 1)² + (z + 2)² = 3 

D. x² + (y + 1)² + (z – 2)² = 64

Câu 14. Cho f(x) là hàm chẵn trên R thỏa mãn 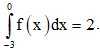Chọn mệnh đề đúng.

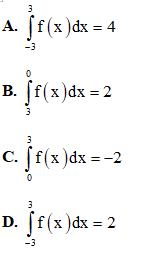
Câu 15. Trong không gian với hệ tọa độ Oxyz, trong các điểm cho dưới đây, điểm nào thuộc trục Oy?

A. N(2; 0; 0)                         B. Q(0; 3; 2)               

C. P(2; 0; 3)                  D. M(0; -3; 0) 

Câu 16. Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi đường cong y = f(x), các đường thẳng x = a, x = b là :

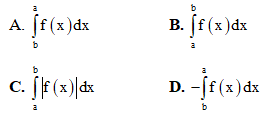
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I (3; 2; -1) và đi qua điểm A(2; 1; 2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?

A. x + y – 3z – 8 = 0 

B. x + y – 3z + 3 = 0

C. x + y + 3z – 9 = 0 

D. x – y – 3z + 3 = 0

Câu 18. Khẳng định nào dưới đây là đúng?

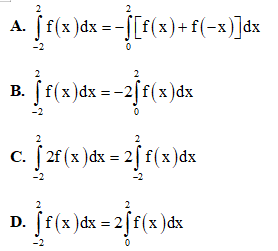
Câu 19. Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (Oxz) là:

A. x = 0                    B. x + z = 0                    

C. z = 0                D. y = 0

Câu 20. Giá trị nào của a để ?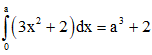

A. 1                       B. 2                                 

C. 0                       D. 3

Câu 21. Trong không gian với hệ tọa độ Oxyz, cho A(1; -1; 0), B(0; 2; 0), C(2; 1; 3). Tọa độ điểm M thỏa mãn 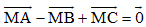 là:

A. (3; 2; -3)             B. (3; -2; 3)                      

C. (3; - 2; -3)        D. (3; 2; 3)

Câu 22. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + 3y + 4z – 5 = 0 và điểm A(1; -3; 1). Tính khoảng cách d từ điểm A đến mặt phẳng (P).

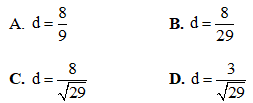
Câu 23. Tìm nguyên hàm của hàm số f(x) = 5^x?

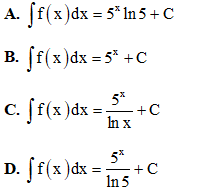
Câu 24. Trong không gian với hệ tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(4; 0; 0), B(0; -2; 0), C(0; 0; 6). Phương trình mặt phẳng (α) là:

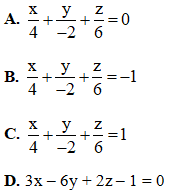
Câu 25. Tìm hàm số F(x) biết F'(x) = sin2x và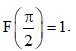

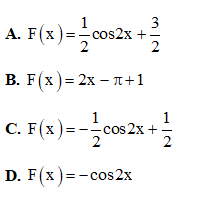
Câu 26. Cho đồ thị hàm số y = f(x)  như hình vẽ và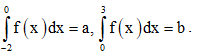

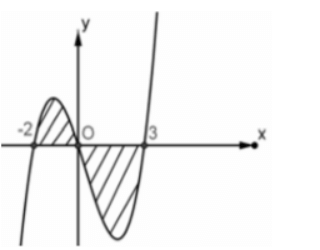
Tính diện tích của phần được gạch chéo theo a, b.

Câu 27. Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y = |x|, y = x² – 2.

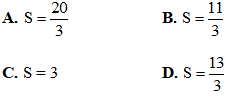
Câu 28. Hàm số nào dưới đây là nguyên hàm của hàm số   ?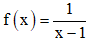

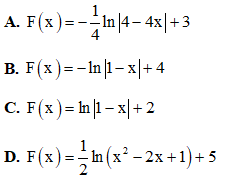
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho A(1; 2; 3), B(-2; 4; 4), C(4; 0; 5). Gọi G là trọng tâm tam giác ABC. Biết điểm M nằm trên mặt phẳng (Oxy) sao cho độ dài đoạn thẳng GM ngắn nhất. Tính độ dài đoạn thẳng GM.

Câu 30. Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;1). Tìm tọa độ điểm M' là hình chiếu vuông góc của M trên mặt phẳng (Oxy).

Câu 31.Tìm tập xác định của hàm số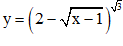

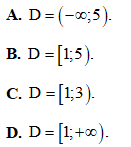
Câu 32. Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB và B’C’. Mặt phẳng (A’MN) cắt cạnh BC tại P. 

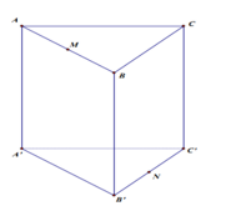
Thể tích khối đa diện MBP.A’B’N’ là:

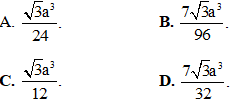
Câu 33. Một ô tô đang đi với vận tốc lớn hơn 72km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là 72km/h, vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc v(t) = 30 – 2t (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét?

A. 100m                           B. 150m                        

C. 175m                        D. 125m

Câu 34. Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị các hàm số y = x² – 2x, y = 0, x = -1, x = 2 quanh quanh trục Ox bằng:

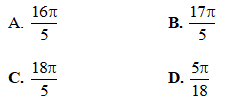
Câu 35. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi Parabol (P): y = x² và đường thẳng d: y = x xoay quanh trục Ox bằng:

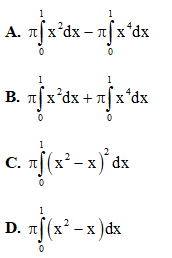
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân giác góc A là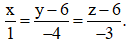Biết rằng điểm M(0;5;3) thuộc đường thẳng AB và điểm N(1; 1; 0)thuộc đường thẳng AC. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC ?

Câu 37. Cần phải làm cái cửa sổ mà phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là a mét (a chính là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi đường kính của hình bán nguyệt). Gọi d là đường kính của hình bán nguyệt. 

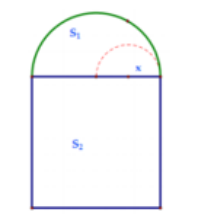
Hãy xác định d để diện tích cửa sổ là lớn nhất.

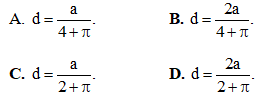
Câu 38. Diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số, trục hoành và hai đường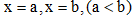 (phần tô đậm trong hình vẽ) tính theo công thức:

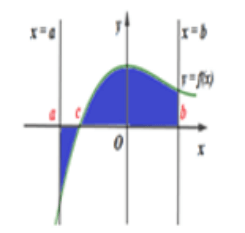
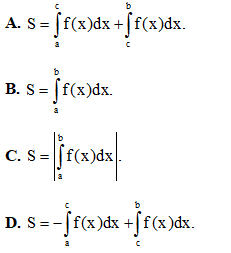
Câu 39.Trong không gian với hệ tọa độ Oxyz, cho 3 điểm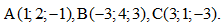Số điểm D sao cho 4 điểm A, B, C, D là 4 đỉnh của một hình bình hành là

A. 3.                           B. 1.                    

C. 1.                          D. 0.

Câu 40. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu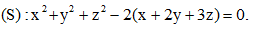Gọi A, B, C lần lượt là giao điểm (khác gốc tọa độ O) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là:

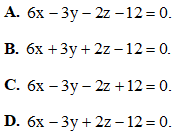
Câu 41. Trong mặt phẳng tọa độ Oxy, gọi (H) là phần mặt phẳng chứa các điểm biểu diễn các số phức z thỏa mãn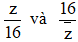có phần thực và phần ảo đều thuộc đoạn [0;1] Tính diện tích S của (H).

A. S = 256

B. S = 64π

C. S = 16(4 - π)

D. S = 32(6 - π)

Câu 42. Biết tích phân 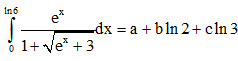 với a, b, c là các số nguyên dương. Tính T = a + b + c.

A.T = 2                      B. T = 1    

               

C. T = 0                      D.T = -1 

Câu 43. Cho hàm số có đạo hàm liên tục trên đoạn 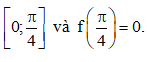Biết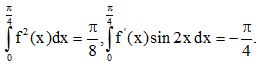Tính tích phân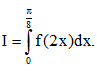

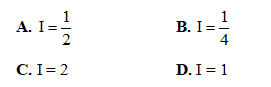
Câu 44. Hình nón đỉnh S, đáy là hình tròn nội tiếp tam giác ABC. Biết rằng AB = BC = 10a, AC = 12a,góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng 45°. Tính thể tích V của khối nón đã cho.

Câu 45. Cho hàm số y = f(x) liên tục trên[1; 4]và thỏa mãn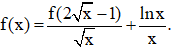Tính tích phân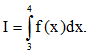

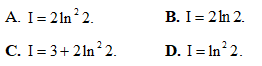
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-3) và mặt phẳng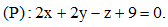Đường thẳng đi qua A và vuông góc với mặt phẳng 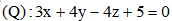cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Tính độ dài MB.

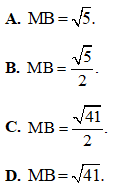
Câu 47. Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật. 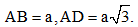 Hình chiếu vuông góc của điểm A’ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD.Tính khoảng cách từ điểm B’ đến (A’BD) .

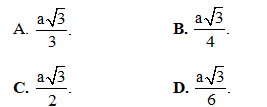
Câu 48. Giải bóng chuyền VTV Cup gồm 12 đội tham dự trong đó có 9 đội bóng nước ngoài 3 đội bóng củaViệt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để ba đội Việt Nam ở 3 bảng khác nhau.

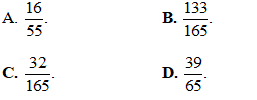
Câu 49. Khoảng cách giữa hai tiệm cận đứng của đồ thị hàm số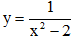bằng:

Câu 50. Tìm tập hợp tất cả các giá trị thực của m để phương trình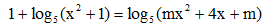  có hai nghiệm phân biệt.

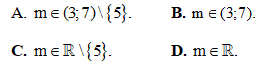
-Hết-

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 12

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 5)

Câu 1: 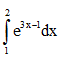 bằng

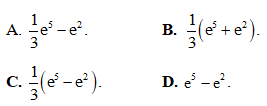
Câu 2: Trong không gian Oxyz, cho mặt cầu 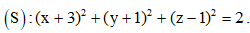. Tâm của (S) có tọa độ là

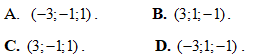
Câu 3: Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức z = - 2 + i?

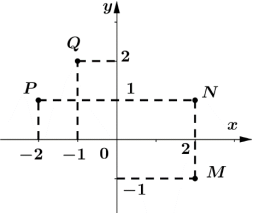
A. M.                            B. N.                          

C. P.                         D. Q.

Câu 4: Tính tích phân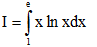

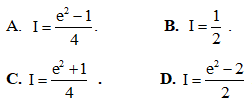
Câu 5: Số phức liên hợp của số phức z  biết 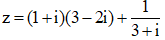 là:

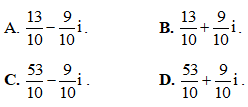
Câu 6: Số phức -3 + 7i có phần ảo bằng

A. -7.                           B. 7i.                               

C. -3.                             D. 7.

Câu 7: Cho số phức z = - 3 + 2i, số phức 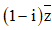 bằng

A. 5 – i.                        B. 1 – 5i.                        

C. – 5 + i.                    D. – 1 – 5i 

Câu 8: Phần thực của số phức z = 5 – 4i là

A. -4.                            B. -5.                              

C. 4.                           D. 5.

Câu 9: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục trên [a; b], trục hoành và hai đường thẳng x = a, x = b được tính theo công thức:

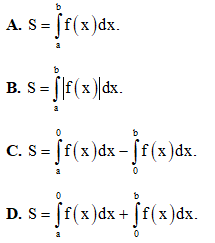
Câu 10: Cho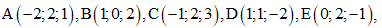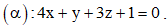Có bao nhiêu điểm đã cho nằm trên mặt phẳng (α)?

A. 4.                  B.  2.                    

C.  1.                   D. 3.

Câu 11: Cho hàm số y = f(x) liên tục trên [1; 4] và thỏa mãn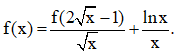Tính tích phân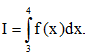

Câu 12: Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm M(1;2;-3) và có một vectơ pháp tuyến ?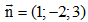

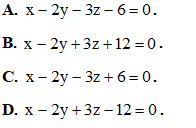
Câu 13:  Cho 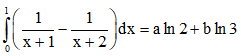 với a, b là các số nguyên.

Mệnh đề  nào dưới đây đúng ?

A. a – 2b = 0.               B. a + b = 2.                  

C. a + b = -2.               D. a + 2b = 0.

Câu 14: Cho hình phẳng D giới hạn bởi đường cong y = e^x, trục hoành và các đường thẳng  x = 0, x = 1. Khối tròn xoay tạo thành khi quay Dquanh trục hoành có thể tích V bằng bao nhiêu ? 

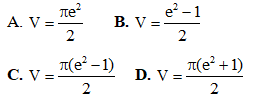
Câu 15: Trong không gian Oxyz, cho hai điểm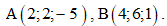 Trung điểm M của đoạn thẳng AB có tọa độ là

   

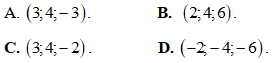
Câu 16: Cho số phức z = 4 + 3i. Môđun của số phức w = 2z + 1 là:

Câu 17: Tìm nguyên hàm của hàm số f(x) = xe^x.

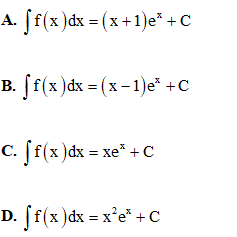
Câu 18: Trong không gian Oxyz, cho hai điểm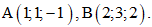Vectơ 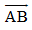 có tọa độ là

  

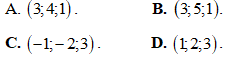
Câu 19: Tìm thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số y = f(x)liên tục trên [a; b], trục Ox và hai đường thẳng x = a, x = b (a < b) xung quanh trục Ox.

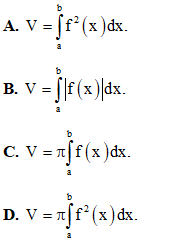
Câu 20: Tìm các số thực x, y thỏa mãn: 

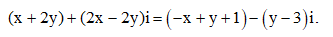
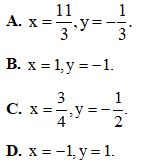
Câu 21: Tìm số phức liên hợp của số phức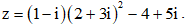 

Câu 22: Giả sử 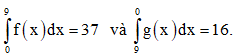  Khi đó  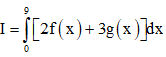bằng:

A. I = 122                    B. I = 26                      

C. I = 143                    D. I = 58

Câu 23: Tính tích phân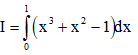

Câu 24: Trong không gian Oxyz, cho mặt phẳng 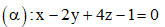.Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng ?

        

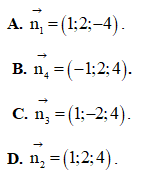
Câu 25: Gọi z₁, z₂ là hai nghiệm phức của phương trình 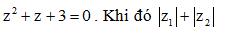bằng

                 

Câu 26: Trong không gian Oxyz, mặt phẳng (Oxz) có phương trình là

A. z = 0.               B. x = 0.                    

C. y = 0.               D. x + y + z = 0.          

Câu 27: Diện tích phần hình phẳng tô đậm trong hình vẽ giới hạn bởi các đường được tính theo công thức nào dưới đây?

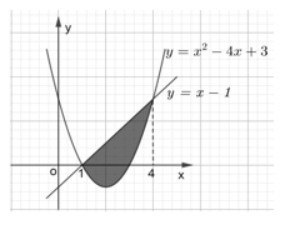
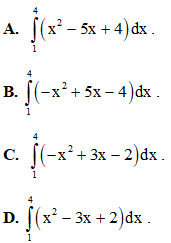
Câu 28: Tích phân 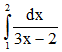 bằng

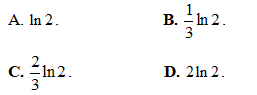
Câu 29: Cho hai số phức z₁ = 2 – i , z₂ = 1 + i. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 2z₁ + z₂ có tọa độ là:

A. (5; -1).                      B. (0; 5).                       

C. (5; 0)                        D. (-1; 5).

Câu 30: Trong không gian Oxyz, cho đường thẳng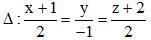 và mặt phẳng 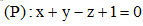. Đường thẳng nằm trong (P) đồng thời cắt và vuông góc với ∆ có phương trình là

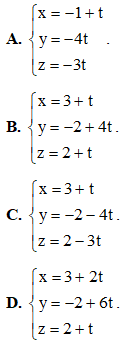
Câu 31:Trên mặt phẳng tọa độ Oxy, điểm nào dưới đây là điểm biểu diễn số phức z = -1 + 2i?

Câu 32: Trong không gian Oxyz, điểm nào dưới đây là hình chiếu vuông góc của điểm A(3; 4; 1) trên mặt phẳng (Oxy)?

Câu 33: Kí hiệu z₁, z₂ là hai nghiệm phức của phương trình z² - z + 6. Tính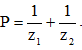

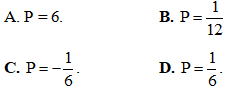
Câu 34:  Tìm số phức z thỏa mãn z + 2 - 3i = 3 - 2i

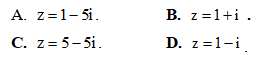
Câu 35: Cho hàm số y = f(x) liên tục trên [1; 4] và thỏa mãn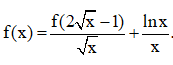Tính tích phân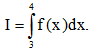

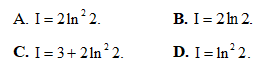
Câu 36: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng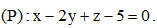 Điểm nào dưới đây thuộc (P) ?

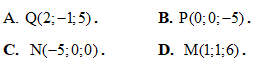
Câu 37: Cho số phức z = 2 + i. Tính |z|.

Câu 38: Giải bóng chuyền VTV Cup gồm 12 đội tham dự trong đó có 9 đội bóng nước ngoài 3 đội bóng củaViệt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để ba đội Việt Nam ở 3 bảng khác nhau.

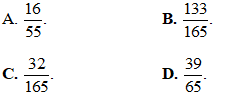
Câu 39: Trong không gian Oxyz, phương trình tham số của đường thẳng d đi qua M(-2;3;1) và có vecto chỉ phương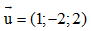  là

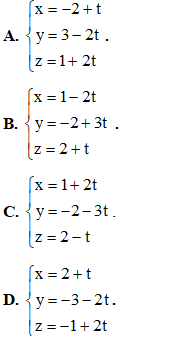
Câu 40: Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng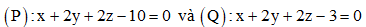bằng

Câu 41: Trong không gian Oxyz, cho đường thẳng 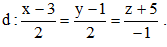 Điểm nào dưới đây thuộc d?

         

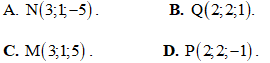
Câu 42: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng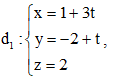 , 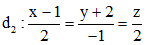và mặt phẳng 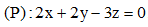. Phương trình nào dưới đây là phương trình mặt phẳng đi qua giao điểm của d₁ và (P), đồng thời vuông góc với d₂.

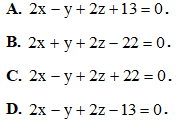
Câu 43:  Cho hàm số có đạo hàm liên tục trên đoạn 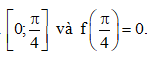Biết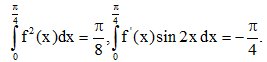Tính tích phân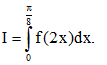

Câu 44: Cho hai hàm số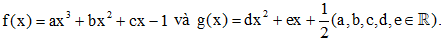Biết rằng đồ thị của hàm số y = f(x) và y = g(x) cắt nhau tại ba điểm có hoành độ lần lượt là -3; -1; 2 (tham khảo hình vẽ bên).

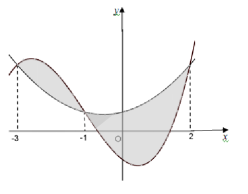
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

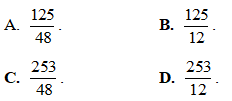
Câu 45: Cho hai số phức z₁  = 3 – 2i và z₂ = 2 + i. Số phức z₁ – z₂ bằng

Câu 46: Nguyên hàm của hàm số f(x) = x³ + x là

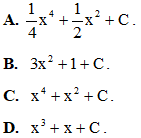
Câu 47: Cho hai số phức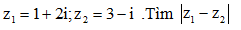

Câu 48: Trong không gian S.ABC, cho mặt cầu 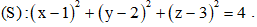. bán kính của mặt cầu đã cho bằng

A. √10.                        B. 16.                              

C. 2.                          D. 4.                               

Câu 49: Cho 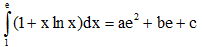 với a, b, c là các số hữu tỉ. Mệnh đề nào dưới đây đúng ?

Câu 50: Giải phương trình :z² - 4z + 11 = 0, kết quả nghiệm là:

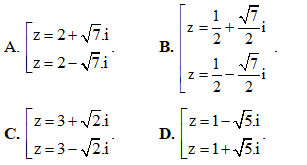
------ HẾT ------

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán 12

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 6)

Câu 1: Cho số phức z = 1 – 2i. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức liên hợp của số phức z?

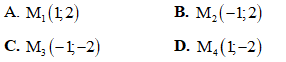
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có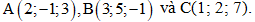 Tìm tọa độ trọng tâm G của tam giác ABC.

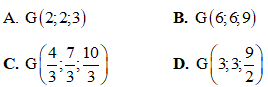
Câu 3: Họ nguyên hàm của hàm số 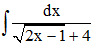 là

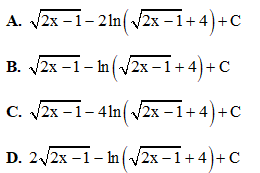
Câu 4: Tính tích phân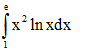

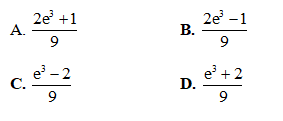
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho điểm H(1; 2; 3). Viết phương trình mặt phẳng (P) đi qua H, cắt các trục x'Ox, y'Oy, z'Oz lần lượt tại các điểm A, B, C  sao cho H là trực tâm của tam giác ABC.

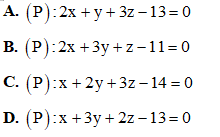
Câu 6: Căn bậc hai của số phức z = -25 là

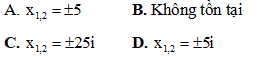
Câu 7: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng 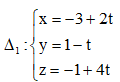và Khẳng định nào sau đây đúng?

A. ∆₁, ∆₂ chéo nhau và vuông góc nhau

B. ∆₁ cắt và không vuông góc với ∆₂

C. ∆₁ cắt và vuông góc với ∆₂

D. ∆₁ và ∆₂ song song với nhau

Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng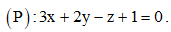 Mặt phẳng (P) có vectơ pháp tuyến là

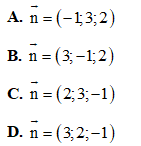
Câu 9: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu 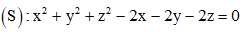 và điểm A(2; 2; 0). Viết phương trình mặt phẳng (OAB), biết rằng điểm B thuộc mặt cầu (S), có hoành độ dương và tam giác OAB đều.

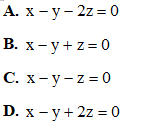
Câu 10: Cho hai số phức z₁ = 7 + 9i và z₂ = 8i. Gọi 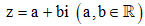là số phức thỏa mãn 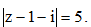Tìm a + b, biết biểu thức  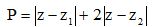đạt giá trị nhỏ nhất.

A. ‒3                          B. ‒7

                       

C. 3                          D. 7

Câu 11: Trong không gian với hệ tọa độ Oxyz, cho hình lăng trụ đứng ABC.A'B'C' có 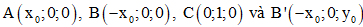trong đó  là các số thực dương và thỏa mãn . Khi khoảng cách giữa hai đường thẳng  và  lớn nhất thì mặt cầu ngoại tiếp hình lăng trụ có bán kính R bằng bao nhiêu?

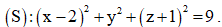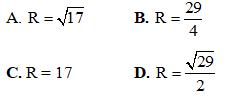
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu Tọa độ tâm I của mặt cầu (S) là

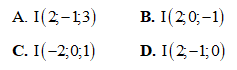
Câu 13: Cho hai số thực a và b (a < b) sao cho 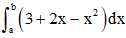 đạt giá trị lớn nhất. Tìm b – a.

A. 2                         B. 4    

                 

C. 6                      D. 8

Câu 14: Gọi h(t) (cm) là mức nước ở một bồn chứa sau khi bơm nước vào bồn được t giây. Biết rằng 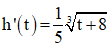 và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 56 giây.

A. 40,8 cm             B. 38,4 cm        

   

C. 36 cm               D. 51,2 cm

Câu 15: Công thức tính diện tích S của hình phẳng giới hạn bởi các đồ thị hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a,  x = b với a < b là

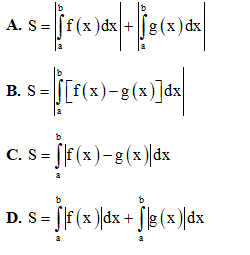
Câu 16: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với 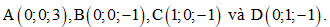. Mệnh đề nào dưới đây sai?

Câu 17: Trong mặt phẳng tọa độ xét ba điểm A, B, C theo thứ tự biểu diễn ba số phức z₁, z₂, z₃ thỏa mãn 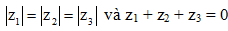và z₁ + z₂ + z₃ = 0. Hỏi tam giác ABC là tam giác gì?

A. Tam giác vuông cân

B. Tam giác vuông có một góc nhọn bằng 30°

C. Tam giác đều

D. Tam giác cân có góc ở đỉnh bằng 30° 

Câu 18: Biết phương trình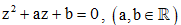 , có một nghiệm phức là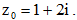Tìm a, b

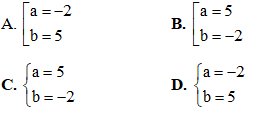
Câu 19: Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và mặt phẳng 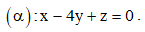Viết phương trình mặt phẳng (β) đi qua A và song song với mặt phẳng (α).

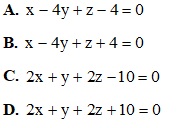
Câu 20: Cho phương trình 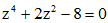có các nghiệm là z₁, z₂, z₃, z₄. Tính giá trị biểu thức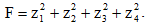

A. F = 4                       B. F = - 4

                       

C. F = 2                          D. F = -2 

Câu 21: Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(4;1;-2). Tọa độ điểm đối xứng với A qua mặt phẳng (Oxz) là

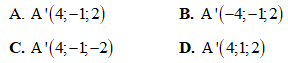
Câu 22: Cho hàm số có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0). Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0, x = 2 bằng 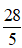 (phần tô đậm trong hình vẽ).

Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = -1, x = 0 có diện tích bằng

Câu 23: Cho hai số phức z₁, z₂ thỏa mãn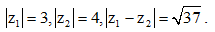  

Xét số phức 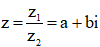. Tìm |b|

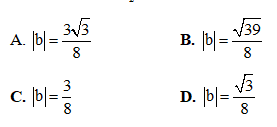
Câu 24: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng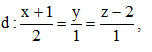 mặt phẳng 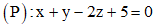và điểm A(1;-1;2). Viết phương trình đường thẳng ∆ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN.

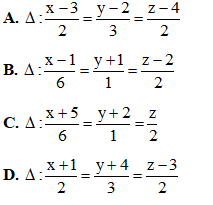
Câu 25: Cho số phức 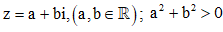thỏa mãn 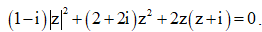Tìm giá trị của biểu thức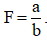

Câu 26: Trong không gian với hệ tọa độ Oxyz, biết rằng tập hợp các điểm M(x, y, z) sao cho |x| + |y| + |z| = 3 là một hình đa diện. Tính thể tích V của khối đa diện đó

A. V = 54                 B. V = 72      

         

C. V = 36               D. V = 27 

Câu 27: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) và mặt phẳng (P) có phương trình lần lượt l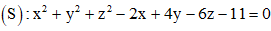à và 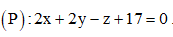Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo một giao tuyến là đường tròn có chu vi bằng 6π

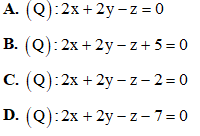
Câu 28: Cho z₁, z₂, z₃, z₄ là bốn nghiệm của phương trình 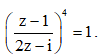Tính giá trị của biểu thức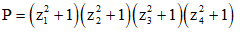

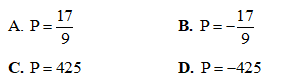
Câu 29: Trong không gian với hệ tọa độ Oxyz, xét các điểm 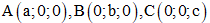 với a, b, c khác 0 và a + 2b + 2c = 6. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm mặt cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ điểm O đến mặt phẳng (P)

A. d = 1                           B. d = √3    

               

C. d = 2                        D. d = 3 

Câu 30: Chất điểm chuyển động theo một đường thẳng sau t giây đạt được vận tốc 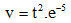(m/s). Tính quãng đường nó đi được trong t giây đầu tiên

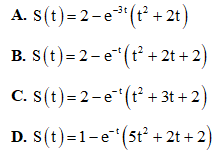
Câu 31: Cho hình phẳng D giới hạn bởi parabol 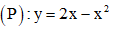 và trục hoành Ox: y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình phẳng D quanh trục Oy

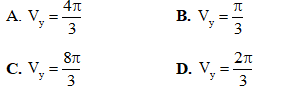
Câu 32: Cho hàm số y = f(x) liên tục và không âm trên R thỏa mãn 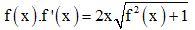và f(0) = 0. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1; 3]. Biết rằng giá trị của biểu thức P = 2M – m có dạng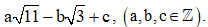Tính a + b + c.  

A. a + b + c = 4           B. a + b + c = 7        

       

C. a + b + c = 6           D. a + b + c = 5  

Câu 33: Biết rằng nghịch đảo của số phức z(z ≠ ± 1) bằng số phức liên hợp của nó. Mệnh đề nào dưới đây đúng?

A. z ∈ R

B. z là một số thuần ảo

C. |z| = -1 

D. |z| = 1 

Câu 34: Tính diện tích hình phẳng giới hạn bởi đường cong y = x², tiếp tuyến với đường cong đó tại điểm có hoành độ bằng 2 và trục Oy.

Câu 35: Trong không gian Oxyz cho đường thẳng Δ có phương trình 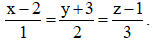 Tìm phương trình tham số của đường thẳng d là hình chiếu vuông góc của Δ trên mặt phẳng (Oyz).

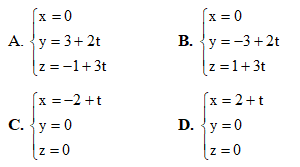
Câu 36: Trong không gian Oxyz, viết phương trình mặt phẳng (P) chứa hai đường thẳng

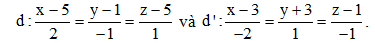
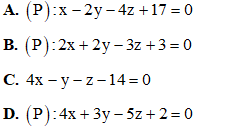
Câu 37: Tính khoảng cách từ điểm A(1; 2; 1) đến đường thẳng .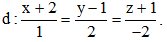

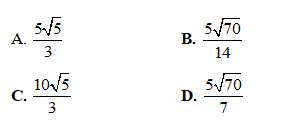
Câu 38: Gọi h(t) (cm) là mức nước ở một bồn chứa sau khi bơm nước vào bồn được t giây. Biết rằng 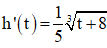 và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 56 giây.

A. 38,4 cm               B. 51,2 cm  

               

C. 36 cm                 D. 40,8 cm

Câu 39: Biết phương trình 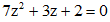có hai nghiệm z₁, z₂ trên tập số phức. Tính giá trị biểu thức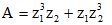

Câu 40: Trong không gian Oxyz cho hình hộp . Biết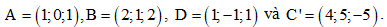Tìm tọa độ đỉnh D'.

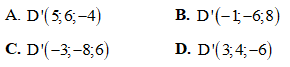
Câu 41: Xét hàm số 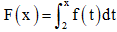 trong đó hàm số y = f(t) có đồ thị như hình vẽ bên.

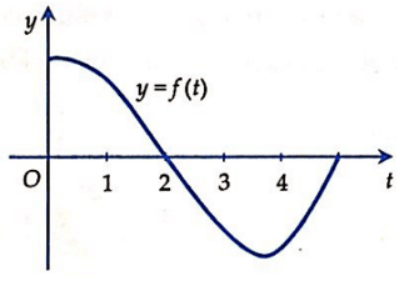
Giá trị nào dưới đây là lớn nhất?

A. F(0)                       B. F(1)      

                 

C. F(2)                       D. F(3) 

Câu 42: Diện tích hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a, x = b (a > b) có công thức tính là:

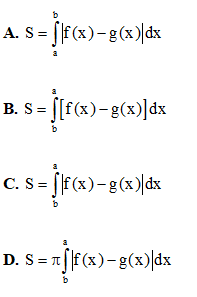
Câu 43: Cho 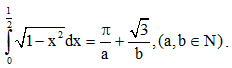Khi đó S = a + b là:

A. 15                 B. 18    

             

C. 14                    D. 20

Câu 44: Cho hình phẳng D giới hạn bởi đồ thị các hàm số 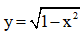và y = 2(1 – x). Biết thể tích khối tròn xoay dc tạo thành khi quay D quanh trục Ox bằng 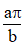, trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm a – b.

A. 71                       B. ‒71    

                     

C. 2                        D. ‒2

Câu 45: Biết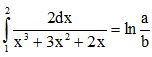 trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm a + b.

A. 59                         B. 58  

                       

C. 57                          D. 56

Câu 46: Trong không gian Oxyz cho ba điểm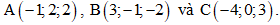Tìm tọa độ điểm I trên mặt phẳng (Oxz) sao cho biểu thức 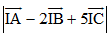đạt giá trị nhỏ nhất.

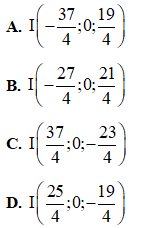
Câu 47: Cho 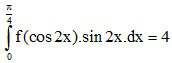. Khi đó  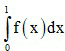có giá trị là:

A. 8                         B. 2      

                 

C. -8                        D.  - 2

Câu 48: Cho 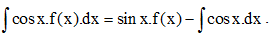Khi đó f(x) là hàm số nào trong các hàm số sau?

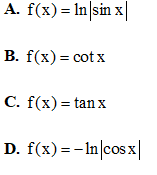
Câu 49: Cho f(x) là một hàm liên tục trên R và a là một số thực lớn hơn 1. Mệnh đề nào dưới đây sai?

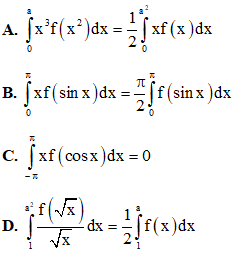
Câu 50: Biết các số phức z₁, z₂, z₃ được biểu diễn bởi ba đỉnh của một hình bình hành nào đó trong mặt phẳng phức. Trong các số phức sau, tìm số phức được biểu diễn bởi đỉnh còn lại.

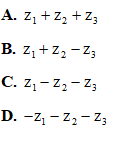
-HẾT-

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---