Giải Toán 9 VNEN Bài 1: Hàm số bậc nhất và đồ thị
MỤC TIÊU
- Biết khái niệm hàm số bậc nhất y = ax + b (a ≠ 0) và cách vẽ đồ thị của nó.
- Hiểu ý nghĩa của đồ thị trong thực tiễn.
A. Hoạt động khởi động
Giải quyết bài toán thực tế và trả lời câu hỏi
Bài toán: Một người thợ điện nhận lắp đặt đường dây và thiết bị điện cho một ngôi nhà sắp xây xong phần thô. Người thợ điện đã mua sắm vật liệu hết 20 000 000 đồng. Tiền công lắp đặt được trả theo ngày với giá là 350 000 đồng/ngày. Hỏi sau x ngày người thợ điện sẽ được thanh toán bao nhiêu tiền (kể cả tiền đã mua sắm vật liệu)?
Hướng dẫn: Gọi t là số tiền mà người thợ điện sẽ được thanh toán sau x ngày làm việc, ta có: t = 350 000.x + 20 000 000.
Trả lời các câu hỏi sau
- Trong bài toán trên, hãy chỉ ra đại lượng nào là hàm số, đại lượng nào là biến số.
- Viết công thức biểu diễn hàm số nói trên và nêu nhận xét về đa thức ở vế phải.
Trả lời:
Gọi t là số tiền mà người thợ điện sẽ được thanh toán sau x ngày làm việc, ta có: t = 350 000.x + 20 000 000.
Vậy sau x ngày làm việc người thợ sẽ được thanh toán 350 000.x + 20 000 000 đồng.
- Trong bài toán trên, đại lượng nào là hàm số là t, biến số là x
- Hàm số: y = 350 000.x + 20 000 000
Hàm số bên phải là phương trình bậc nhất một ẩn.
B. Hoạt động hình thành kiến thức
1. a) Đọc kĩ nội dung sau
Ở lớp 7 ta đã làm quen với những hàm số được cho bằng bảng hoặc bằng công thức … Trong chương này ta sẽ làm quen với những hàm số được cho bởi công thức dạng y = ax + b (a ≠ 0) (với về phải là đa thức bậc nhất một biến). Đó là các hàm số bậc nhất.
Hàm số bậc nhất là hàm số được cho bởi công thức: y = ax + b, trong đó a, b là các số thực cho trước và a ≠ 0.
Khi b = 0, hàm số có dạng y = ax.
b) Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
A. y = 2x
B. y = 2x + 3
C. y = 4/x
D. y = 0,1 – 3x
Mẫu: Hàm số y = 2x là hàm số bậc nhất.
Hàm số y = 2x + 3 là hàm số bậc nhất
Hàm số y = 4/x không phải là hàm số bậc nhất
Hàm số y = 0,1 - 0,3x là hàm số bậc nhất.
c) Cho hàm số y = f(x) = 3x – 2. Tìm:
• Giá trị của y khi x bằng 2 ; -3,5 ; 1,8 ; 0
• Giá trị của x khi giá trị tương ứng của y là 46 ; -4 ; 0 ; 1
Mẫu:
• Khi x = 2 thì y = f(2) = 3.2 – 2 = 4
• Nếu y = f(x) = 3x – 2 = 46, suy ra x = 16
Trả lời:
* Khi x = 2 thì y = f(x) = 3.2 - 2 = 4
Khi x = -3,5 thì y = f(x) = 3.(-3,5) - 2 = -12,5
Khi x = 1,8 thì y = f(x) = 3.1,8 - 2 = 3,4
Khi x = 0 thì y = f(x) = 3.0 - 2 = -2
* Nếu y = f(x) = 3x - 2 = 46, suy ra x = 16
Nếu y = f(x) = 3x - 2 = -4, suy ra x = -2/3
Nếu y = f(x) = 3x - 2 = 0, suy ra x = 2/3
Nếu y = f(x) = 3x - 2 = 1, suy ra x = 1
2. a) Thực hiện ví dụ sau
Ví dụ: Xét hàm số y = 2x + 3
- Tính giá trị tương ứng của y với giá trị đã cho của biến x, rồi điền vào bảng:
| x | -1 | -2 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y = 2x + 3 |
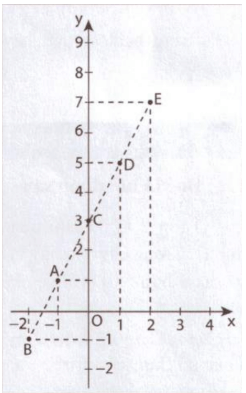
- Xác định các điểm A(-1; 1); B(-2; -1); C(0; 3); D(1; 5); E(2; 7) trên mặt phẳng tọa độ Oxy
- Nối các điểm vừa xác định rồi nêu nhận xét về
hình dạng của đồ thị hàm số y = 2x + 3.
b) Đọc kĩ nội dung sau
Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng.
3. a) Cách vẽ đồ thị của hàm số y = ax + b (a ≠ 0)
- Nếu b = 0, thì y = ax. Đồ thị của hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A(1;a).
- Nếu b ≠ 0 (và a ≠ 0):
Vì đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng, nên để vẽ đồ thị hàm số, ta chỉ cần xác định được hai điểm phân biệt A, B nào đó thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó.
Trong thực hành, ta thường xác định hai điểm đặc biệt là giao điển của đồ thị với hai trục tọa độ.
Bước 1: Cho x = 0 thì y = b, ta được điểm A(0;b) (thuộc trục tung Oy).
Bước 2: Cho y = 0 thì x = -b/a , ta được điểm B(-b/a, 0) (thuộc trung hoành Ox).
Khi đó, đồ thị hàm số là đường thẳng AB.
b) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
a) y = x – 2;
b) y = x + 3
Trả lời:
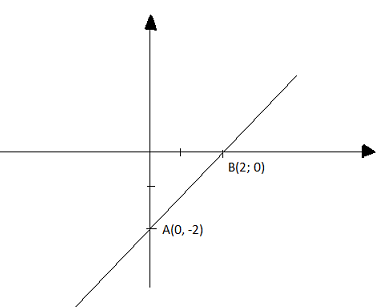
* y = x - 2
Cho x = 0 thì y = -2, ta được điểm A(0; -2)
Cho y = 0 thì x = 2, ta được điểm B(2; 0)
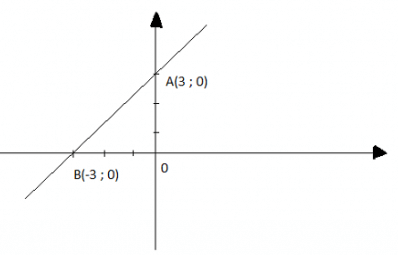
* y = x + 3
Cho x = 0 thì y = 3, ta được điểm A(0; 3)
Cho y = 0 thì x = - 3, ta được điểm B(-3; 0)
c) Chú ý:
Đồ thị của hàm số y = ax + b (a ≠ 0) còn được gọi là đường thằng y = ax + b; b được gọi là tung độ gốc của đường thẳng.
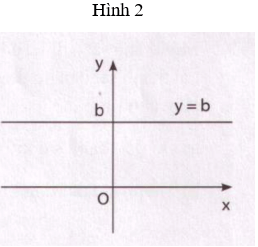
Khi a = 0, ta có y = b là một hàm hẳng. Đồ thị hàm số y = b là đường thẳng song song với trục Ox, nếu b ≠ 0; và trùng với trục Ox, nếu b = 0 (hình 2)
C. Hoạt động luyện tập
1. Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
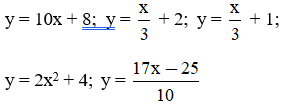
Lời giải:
Hàm số y = 10x + 8 là hàm số bậc nhất
Hàm số
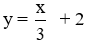
Hàm số
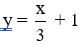
Hàm số
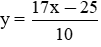
2. Cho hàm số bậc nhất y = 10x + 1. Tìm:
a) Giá trị của y tương ứng với các giá trị của x bằng 2 ; -1,5 ; 0 ; 3/2
b) Giá trị của x tương ứng với các giá trị của y là -9 ; -4 ; 6 ; 31
Lời giải:
a) Khi x = 2 thì y = f(x) = 10.2 + 1 = 21
Khi x = -1,5 thì y = f(x) = 10.(-1,5) + 1 = -14
Khi x = 0 thì y = f(x) = 10.0 + 1 = 1
Khi x = 3/2 thì y = f(x) = 10. 3/2 + 1 = 16
b) Nếu y = f(x) = 10x + 1 = -9, suy ra x = -1
Nếu y = f(x) = 10x + 1 = -4, suy ra x = -0,5
Nếu y = f(x) = 10x + 1 = 6, suy ra x = 0,5
Nếu y = f(x) = 10x + 1 = 31, suy ra x = 3.
3. Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
a) y = 0,5x – 2;
b) y = -2x – 1
c) y = -0,5x + 2;
d) y = (1/3)x – 1
Lời giải:
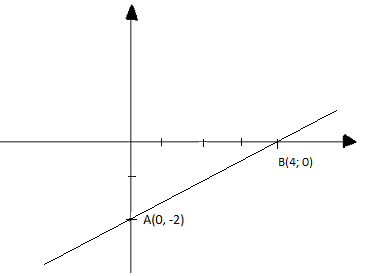
a) y = 0,5x - 2
Cho x = 0 thì y = -2, ta được điểm A(0; -2)
Cho y = 0 thì x = 4, ta được điểm B(4; 0)
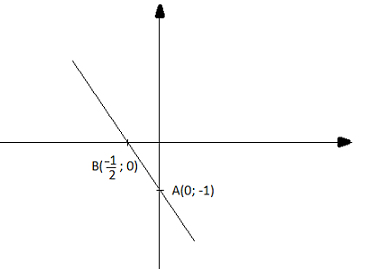
b) y = -2x - 1
Cho x = 0 thì y = -1, ta được điểm A(0; -1)
Cho y = 0 thì x = -1/2, ta được điểm B(-1/2; 0)
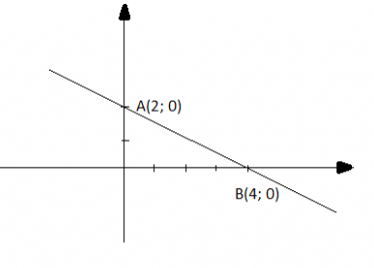
c) y = -0,5x + 2
Cho x = 0 thì y = 2, ta được điểm A(0; 2)
Cho y = 0 thì x = 4, ta được điểm B(4; 0)
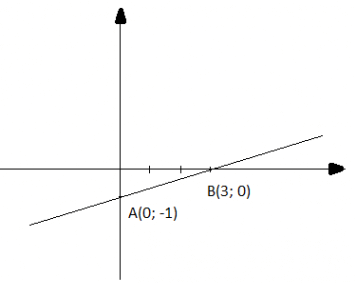
d) y = (1/3)x - 1
Cho x = 0 thì y = - 1, ta được điểm A(0; -1)
Cho y = 0 thì x = 3, ta được điểm B(3; 0)
4. Không vẽ đồ thị hàm số y = 1,5x + 10, hãy cho biết trong các điểm sau, điểm nào thuộc đồ thị hàm số đã cho?
A(10; 25) ; B(-2; 7) ; C(4; -4) ; D(0; 10)
Lời giải:
Ta thay các điểm vào hàm số y = 1,5x + 10, điểm nào thỏa mãn thì điểm đó thuộc đồ thị hàm số
A(10; 25): 25 = 1,5.10 + 10 suy ra A thuộc đồ thị
B(-2; 7): 7 = 1,5.(-2) + 10 suy ra B thuộc đồ thị
C(4; -4): -4 ≠ 1,5.4 + 10 suy ra C không thuộc đồ thị
D(0; 10): 10 = 1,5.0 + 10 suy ra D thuộc đồ thị
Vậy A(10; 25); B(-2; 7); D(0; 10) thuộc đồ thị hàm số.
:5. Vẽ đồ thị của các hàm số:
a) y = -2;
b) y = 1
c) y = 2,5
d) y = -1,5
Lời giải:
a) y = -2
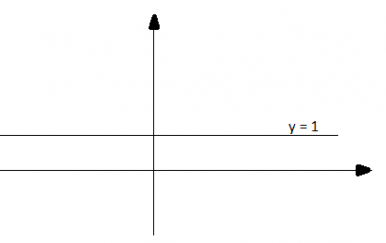
b) y = 1
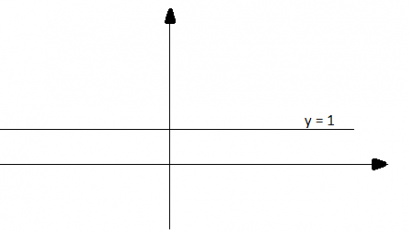
c) y = 2,5
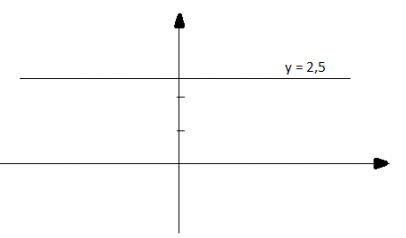
d) y = -1,5
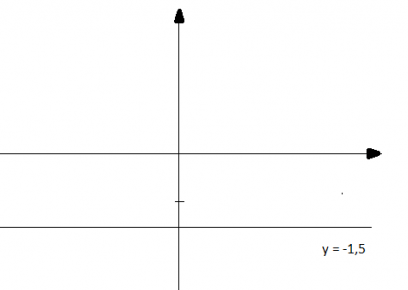
6. Một cái can có dung tích 45l không chứa chất lỏng thì cân nặng 5kg, khối lượng của mỗi lít chất lỏng là 0,9kg. Hỏi rằng khi chứa p lít chất lỏng thì khối lượng của cái can này là bao nhiêu kg?
Bài làm:
Gọi khối lượng của cái can là t (kg)
Can có dung tích 45l và khối lượng khi không chứa chất lỏng của can là 5kg
Ta có: t = 0,9.p + 5
Vậy khi chứa p lít chất lỏng thì khối lượng cái can này là t = 0,9.p + 5 (kg).
D. Hoạt động vận dụng
1. Cho hàm số bậc nhất y = kx – 3. Tìm k, biết rằng đồ thị hàm số đi qua điểm A(-1; 0,5).
Lời giải:
Đồ thị hàm số y = kx - 3 đi qua điểm A(-1; 0,5) tức là:
0,5 = k.(-1) - 3 ⇔ k = - 3,5
Vậy k = - 3,5.
2. Với giá trị nào của a thì điểm A(a; 2a – 1) thuộc đồ thị hàm số:
a) y = -2x + 3
b) y = -x + 5
c) f(x) = 3x – 1
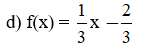
Lời giải:
Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì điểm A phải thỏa mãn hàm số
a) Ta có: y = -2x + 3 = -2.a + 3 = -2a + 3. Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì 2a - 1 = -2a + 3 ⇔ a = 1
b) Ta có: y = -x + 5 = -a + 5. Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì 2a - 1 = -a + 5 ⇔ a = 2
c) Ta có: f(x) = 3x - 1 = 3a - 1. Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì 2a - 1 = 3a - 1 ⇔ a = 0
d) Ta có:
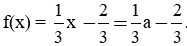
Để điểm A (a; 2a - 1) thuộc đồ thị hàm số thì
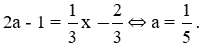
3. Một thanh sắt ở nhiệt độ t = 0oC có chiều dài là l = 10m. Khi nhiệt độ thay đổi thì chiều dài thanh sắt dãn nở theo công thức l = 10(l + 0,000012t), trong đó -100oC < t < 200oC. Hãy cho biết:
a) Độ dài thanh sắt khi t bằng 0oC; 50oC ; -50oC ;
b) Thanh sắt dài thêm bao nhiêu mi-li-mét nếu nhiệt độ tăng từ -20oC đến 80oC
Lời giải:
a) Khi t bằng 0oC thì độ dài thanh sắt là l = 10(1 + 0,000012t) = 10(1 + 0,000012.0) = 10oC
Khi t bằng 50oC thì độ dài thanh sắt là l = 10(1 + 0,000012t) = 10(1 + 0,000012.50) = 10,006oC
Khi t bằng −50oC thì độ dài thanh sắt là l = 10(1 + 0,000012t) = 10(1 + 0,000012.(- 50)) = 9,994oC
b) Khi t bằng −20oC thì độ dài thanh sắt là l1 = 10(1 + 0,000012t) = 10(1 + 0,000012.(- 20)) = 9,9976oC
Khi t bằng 80oC thì độ dài thanh sắt là l2 = 10(1 + 0,000012t) = 10(1 + 0,000012.80) = 10,0096oC
Suy ra khi nhiệt độ tăng từ −20oC đến 80oC thì độ dài thanh sắt tăng thêm là l' = l2 - l1 = 10,0096 - 9,9976 = 0,012oC.
4. Đồ thị của hàm số y = √3x + √3 được vẽ bằng compa và thước thẳng như hình 3.
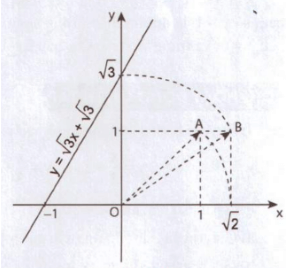
Hãy tìm hiểu cách vẽ đó rồi nêu lại cách thực hiện.
Áp dụng:
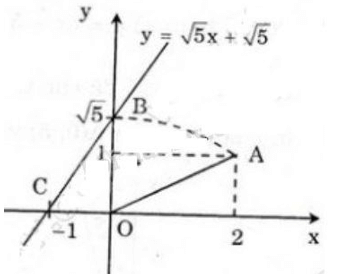
Vẽ đồ thị của hàm số y = √5x + √5 bằng compa và thước thẳng.
Lời giải:
a)
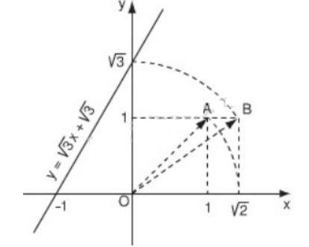
Vẽ đồ thị hàm số y = √3 x+√3
Cho x = 0 thì y = √3 ⇔ M(0; √3)
Cho y = 0 thì x = - 1 ⇔ N(- 1; 0)
Đồ thị hàm số y = √3 x + √3 là đường thẳng đi qua hai điểm M(0; √3) và N(- 1; 0)
Ta xác định vị trí của M(0; √3) trên trục tung;
Bước 1: Xác định vị trí A(1; 1) trên mặt phẳng tọa độ Oxy, theo định lí Py-ta-go ta có: OA2 = 12 + 12 = 2 ⇔ OA = √2
Bước 2: Dùng compa vẽ cung tròn tâm O bán kính OA = √2 cắt Ox tại C thì hoành độ của C là √2
Bước 3: Xác định điểm B( ; 1). Theo định lí Py-ta-go ta có: OB2 = (√2)2 + 12 = 3
Bước 4: Dùng compa vẽ cung tròn tâm O bán kính OB = √3 cắt Oy tại √3 ta được M(0; √3)
Bước 5: Kẻ đường thẳng đi qua hai điểm N và N ta được đồ thị hàm số y = √3 x + √3
b) Tương tự như cách làm câu a, ta được đồ thị của hàm số y = √5 x + √5:
E. Hoạt động tìm tòi, mở rộng
Em có biết?
a) Mối quan hệ giữa độ F và độ C
Độ Celsius (còn gọi là độ C) là thang nhiệt được đặt tên theo nhà thiên văn học người Thụy Điển Ander Celsius (1701 – 1744). Theo đó, nước đóng băng ở 0oC và sôi ở 100oC.
Độ Fahrenheit (còn gọi là độ F) là thang nhiệt được đặt tên theo nhà vật lí người Đức Gabriel Fahrenheit (1686 – 1736). Theo đó, nước đóng băng ở 32oF và sôi ở 212oF.
b)
Nhiệt độ ở Canada được đo bằng độ C, nhưng ở Hoa Kỳ nhiệt độ được đo bằng độ F.
Hoa Kỳ và Canada là hai nước láng giềng. Vì vậy khi di chuyển từ nước này sang nước kia cũng cần biết cách đọc thang đo nhiệt độ.
Mối quan hệ giữa số đo độ F (kí hiệu là ĐF) và số đo độ C (kí hiệu là ĐC) như sau:
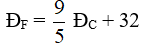
| Canada(oC) | -10 | 0 | 20 | 25 |
|---|---|---|---|---|
| Hoa Kỳ (oF) | 14 | 32 | 68 | 77 |
c) Điền số thích hợp vào ô trống trong bảng sau đây (chính xác đến một chữ số thập phân)

| ĐC | 1 | 37 | |||
|---|---|---|---|---|---|
| ĐF | 1 | 0 | 100 |
Xem thêm các bài Giải bài tập Toán lớp 9 chương trình VNEN hay khác:
- Bài 2: Hệ số góc của đường thẳng y = ax + b
- Bài 3: Đường thẳng song song và đường thẳng cắt nhau
- Bài 4: Tính chất đồng biến, nghịch biến của hàm số y = ax + b
- Bài 5: Ôn tập chương II
Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:
- Giải sách bài tập Toán 9
- Chuyên đề Toán 9 (có đáp án - cực hay)
- Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
- Các dạng bài tập Toán 9 cực hay
- Đề thi Toán 9
- Đề thi vào 10 môn Toán
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giải bài tập Toán lớp 9 VNEN của chúng tôi được biên soạn bám sát theo chương trình Hướng dẫn học Toán 9 chương trình mới VNEN Tập 1 & Tập 2.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 9 Global Success
- Giải sgk Tiếng Anh 9 Smart World
- Giải sgk Tiếng Anh 9 Friends plus
- Lớp 9 Kết nối tri thức
- Soạn văn 9 (hay nhất) - KNTT
- Soạn văn 9 (ngắn nhất) - KNTT
- Giải sgk Toán 9 - KNTT
- Giải sgk Khoa học tự nhiên 9 - KNTT
- Giải sgk Lịch Sử 9 - KNTT
- Giải sgk Địa Lí 9 - KNTT
- Giải sgk Giáo dục công dân 9 - KNTT
- Giải sgk Tin học 9 - KNTT
- Giải sgk Công nghệ 9 - KNTT
- Giải sgk Hoạt động trải nghiệm 9 - KNTT
- Giải sgk Âm nhạc 9 - KNTT
- Giải sgk Mĩ thuật 9 - KNTT
- Lớp 9 Chân trời sáng tạo
- Soạn văn 9 (hay nhất) - CTST
- Soạn văn 9 (ngắn nhất) - CTST
- Giải sgk Toán 9 - CTST
- Giải sgk Khoa học tự nhiên 9 - CTST
- Giải sgk Lịch Sử 9 - CTST
- Giải sgk Địa Lí 9 - CTST
- Giải sgk Giáo dục công dân 9 - CTST
- Giải sgk Tin học 9 - CTST
- Giải sgk Công nghệ 9 - CTST
- Giải sgk Hoạt động trải nghiệm 9 - CTST
- Giải sgk Âm nhạc 9 - CTST
- Giải sgk Mĩ thuật 9 - CTST
- Lớp 9 Cánh diều
- Soạn văn 9 Cánh diều (hay nhất)
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Toán 9 - Cánh diều
- Giải sgk Khoa học tự nhiên 9 - Cánh diều
- Giải sgk Lịch Sử 9 - Cánh diều
- Giải sgk Địa Lí 9 - Cánh diều
- Giải sgk Giáo dục công dân 9 - Cánh diều
- Giải sgk Tin học 9 - Cánh diều
- Giải sgk Công nghệ 9 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 9 - Cánh diều
- Giải sgk Âm nhạc 9 - Cánh diều
- Giải sgk Mĩ thuật 9 - Cánh diều




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

