Giải Toán 9 VNEN Bài 3: Tỉ số lượng giác của góc nhọn

MỤC TIÊU

- Biết được ý nghĩa của các tỉ số lượng giác và nhớ được công thức tính các tỉ số lượng giác của các góc nhọn trong tam giác vuông.

- Nhớ được các giá trị lượng giác của một số góc nhọn đặc biệt (30^o ; 45^o ; 60^o).

- Trình bày được mối liên hệ giữa các tỉ số lượng giác của hai góc phụ nhau.

- Vận dụng được các công thức tỉ số lượng giác vào các bài tập tính toán trong tam giác.

A. Hoạt động khởi động

Cùng tìm hiểu tình huống tính độ dốc của đoạn đường

Thầy giá giao cho cả lớp một đề bài như sau:

Xét một đoạn đường dốc dài 500m từ chân dốc lên đến đỉnh dốc. Biết rằng độ cao của dốc tính từ chân dốc là 100m. Người ta muốn tính toán góc tạo bởi đoạn đường dốc với mặt phẳng nằm ngang (còn gọi là góc dốc) để đưa ra những tư vấn hợp lí cho các phương tiện giao thông khi đi qua đoạn đường này. Liệu có cách nào để tính được góc dốc của đoạn đường này không?

Lan suy nghĩ một lúc rồi tiến hành theo các bước:

+ Vẽ hình mô phỏng đoạn đường dốc (chú ý vẽ theo đúng tỷ lệ các độ dài, hình 30)

+ Dùng thước đo góc để đo góc dốc trên hình mà Lan vừa vẽ.

Từ đó Lan đã tìm được câu trả lời cho câu hỏi của thầy giáo và được khen ngợi.

B. Hoạt động hình thành kiến thức

1. a) Thực hiện các hoạt động sau

- Thực hiện theo các bước mà Lan đã làm như trên và cho biết số đo góc dốc mà em nhận được;

- So sánh kết quả với các bạn trong lớp

Để xác định số đo các góc nhọn trong tam giác vuông thông qua độ dài các cạnh, ta sử dụng các công thức tỉ số lượng giác.

b) Cho góc nhọn α. Vẽ một tam giác vuông có một góc nhọn bằng α(h.31).

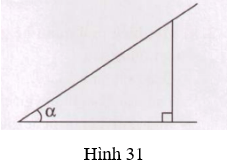
Đọc kĩ nội dung sau

- Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.

- Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α , kí hiệu là cosα.

- Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α , kí hiệu là tan (hoặc tgα).

- Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α , kí hiệu là cot ( hoặc cotgα).

Chú ý: Các tỉ số sin α; cosα; tanα; cotα được gọi là các tỉ số lượng giác của góc .

Điền vào chỗ trống để hoàn thành các công thức sau (h.32):

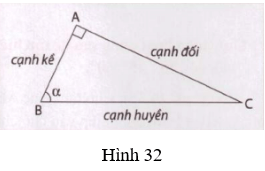
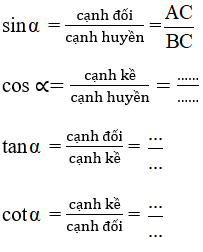
Trả lời:

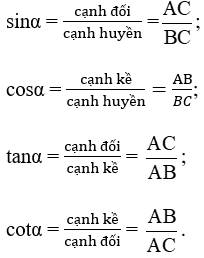
c) Làm bài tập sau

Bài tập 1. Tính các tỉ số lượng giác của góc nhọn trong hình 33 sau:

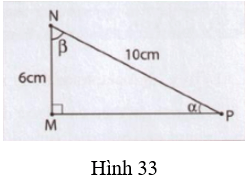
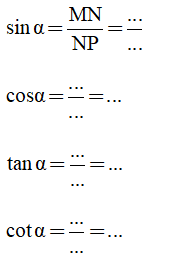
Trả lời:

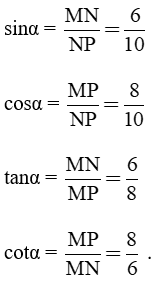
2. a) Tìm hiểu mối quan hệ giữa tỉ số lượng giác của hai góc phụ nhau thông qua hoạt động sau

- Quan sát hình 33

- Tính các tỉ số lượng giác của góc β

- Nhận xét mối quan hệ giữa α và β, sinα và cosβ ; cosα và sinβ ; tanα và cotβ; cotα và tanβ

Trả lời:

- Tính:

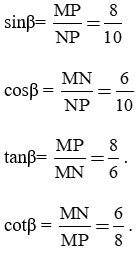
- Nhận xét:

α + β = 900

sinα = cosβ

cosα = sinβ

tanα = cotβ

cotα = tanβ.

b) Đọc kĩ nội dung sau

Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.

Chẳng hạn, trong tam giác vuông ABC (vuông tại A) (h.34):

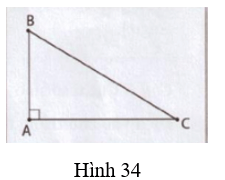
sin B = cos C

sin C = cos B

tan B = cot C

tan C = cot B

c) Thực hiện hoạt động sau để tìm hiểu các tỉ số lượng giác của góc 30^o; 45^o; 60^o:

Bài tập 2. (h.35). Cho tam giác ABC vuông cân tại A, AB = 5cm. Điền tiếp vào chỗ chấm (…):

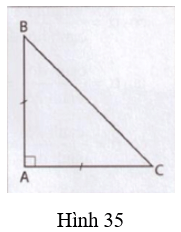
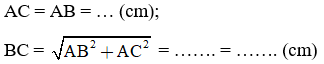
Tam giác ABC vuông cận tại A nên ∠(ABC) = 45^o;

Trả lời:

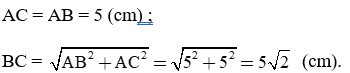
Tam giác ABC vuông cận tại A nên ∠(ABC) = 45^o;

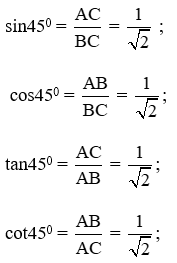
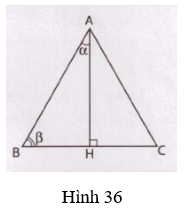
Bài tập 3. (h.36) Cho tam giác ABC đều cạnh 4cm, đường cao AH. Tính số đo độ dài các cạnh AB, AH, BH của tam giác AB, từ đó tính tỉ số lượng giác của các góc α; β.

Trả lời:

Gọi tên các góc như trong hình vẽ

Tam giác ABC đều nên AB = AC = BC = 4cm và ∠(ABC) = ∠(BAC) = ∠(ACB) = 60^o

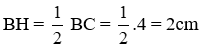
Theo định lý Py-ta-go ta có:

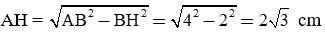
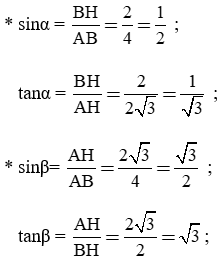
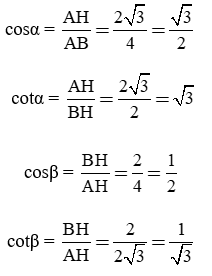
C. Hoạt động luyện tập

Bài tập 1. Cho tam giác ABC vuông tại C, AC = 0,9cm, BC = 1,2cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.

Lời giải:

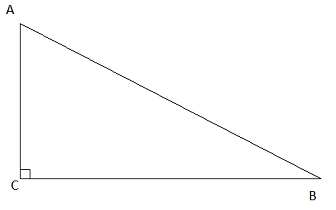
Áp dụng định lý Py-ta-go trong tam giác ABC ta có:

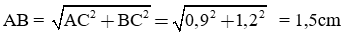
Ta có:

Ta có: ∠A + ∠B = 90^o nên:

Bài tập 2. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45^o:

sin 60^o ; cos63^o ; tan52^o ; cot81^o.

Lời giải:

Áp dụng tính chất: Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia

Do đó:

sin60^o = cos30^o

cos63^o = sin27^o

tan52^o = cot38^o

cot81^o = tan9^o

Bài tập 3. Vẽ tam giác ABC vuông tại A, B = α, biết:

a) tanα = 2

b) sinα = 3/5

Bài làm:

a) Ta có:

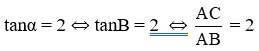
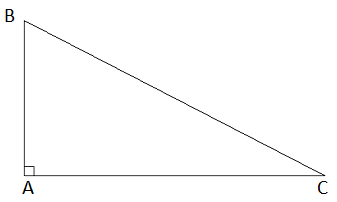
Ta được hình vẽ:

b) Ta có;

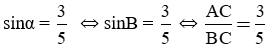
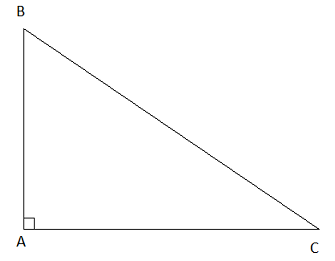
Ta được hình vẽ:

Bài tập 4. Cho tam giác ABC vuông tại A, BC = 10cm, cosB = 0,8

a) Tính các cạnh AB, AC

b) Tính các tỉ số lượng giác của góc C

Lời giải:

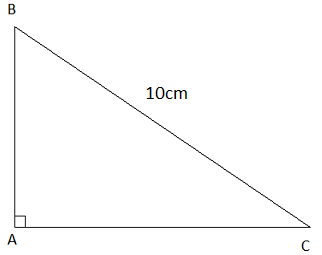
a) Ta có:

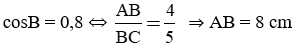
Áp dụng định lý Py-ta-go ta được AC² = BC² − AC² = 10² − 8² = 36 ⇒ AB = √36 = 6 cm

b) Ta có:

D.E. Hoạt động vận dụng và tìm tòi, mở rộng

Em có biết?

Nhà mái ngói dốc (mái dốc) là một trong những hình thức kiến trúc phổ biến nhất ở Việt Nam. Mái dốc kiểu truyền thống phù hợp với cả kiến trúc phương Đông và phương Tây, phù hợp với khí hậu nhiệt đới nóng ẩm của Việt Nam đồng thời lại tương đối rẻ tiền, dễ thi công. Mái dốc thường có ba loại sau đây (h.37):

Mái một dốc; Mái hai dốc; Mái bốn dốc.

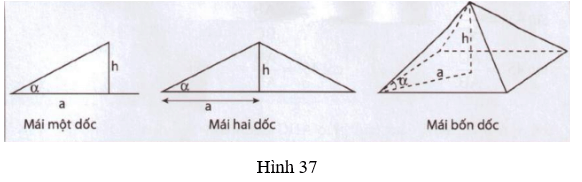
Trong xây dựng, người ta thường sử dụng đến khái niệm “độ dốc” của mái ngói, được tính bằng công thức:

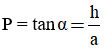
Với h: chiều cao, a : cạnh đáy, P thường tính theo đơn vị %

a) Mái dốc là mái có độ dốc P > 8%. Em hãy tính góc dốc α tối thiểu của mái dốc.

b) Một ngôi nhà lợp mái ngói hai dốc có độ dốc 50%. Biết chiều cao của mái dốc là 1,2m. Tính bề rộng phần mái dốc của ngôi nhà.

c) Liệu có tồn tại mái có độ dốc 100% không? Vì sao?

Bài làm:

a) Mái dốc là mái có độ dốc > 8%, tức là :

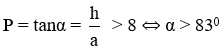
b) Ta có công thức tính độ dốc của mái là:

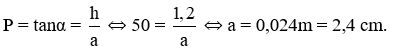
c) Giả sử tồn tại mái dốc 100%, tức là khi đó:

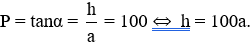
Xem thêm các bài Giải bài tập Toán lớp 9 chương trình VNEN hay khác:

• Bài 4: Sử dụng máy tính cầm tay để tính tỉ số lượng giác
• Bài 5: Một số hệ thức về cạnh và góc trong tam giác vuông
• Bài 6: Luyện tập
• Bài 7: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn
• Bài 8: Ôn tập chương I

Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:

• Giải sách bài tập Toán 9
• Chuyên đề Toán 9 (có đáp án - cực hay)
• Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
• Các dạng bài tập Toán 9 cực hay
• Đề thi Toán 9
• Đề thi vào 10 môn Toán

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---