Giải Toán 9 VNEN Bài 2: Luyện tập

MỤC TIÊU

- Vận dụng được một cách linh hoạt các hệ thức vào việc tìm các yếu tố chưa biết về cạnh, đường cao trong tam giác vuông.

- Ứng dụng được các hệ thức vào giải các bài toán thực tế có liên quan.

A.B. Hoạt động khởi động và hình thành kiến thức

Sơ đồ tư duy các hệ thức lượng trong tam giác vuông

Em vẽ sơ đồ tư duy theo các bước sau:

- Liệt kê tất cả các kiến thức liên quan đến tính chất, định lí, hệ thức lượng trong tam giác vuông;

- Chỉ ra các mối liên hệ giữa các công thức;

- Bắt tay vào vẽ sơ đồ tư duy

C. Hoạt động luyện tập

1. Tìm x, y trong mỗi hình vẽ sau:

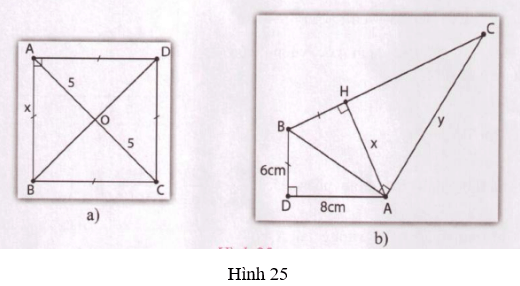
Hướng dẫn:

Hình 25a

- Tứ giác ABCD là hình thoi có góc A vuông nên ABCD là hình vuông

- Áp dụng công thức b² = ab’ cho tam giác vuông ABC, đường cao BO

Hình 25b

- ΔABD = ΔABH (cạnh huyền – cạnh góc vuông) ⇒ x = AD = 8cm

- Áp dụng định lí Py-ta-go:

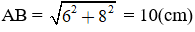
- Áp dụng công thức (4) cho tam giác vuong ABC, để tính AC = y.

Lời giải:

* Hình 25a

Ta có tứ giác ABCD là hình thoi có góc A vuông nên ABCD là hình vuông

Áp dụng công thức b² = ab' cho tam giác vuông ABC, ta có:

x² = 5.(5 + 5)

⇒ x = 5

* Hình 25b

Ta có: ΔABD = ΔABH (cạnh huyền - cạnh góc vuông)

⇒ x = 8cm

Áp dụng định lý Py-ta-go ta có:

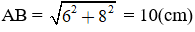
Áp dụng công thức , ta có:

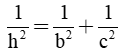
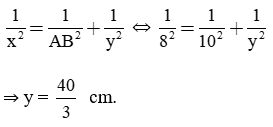
2. Cho tam giác vuông với các cạnh góc vuông có độ dài là 3cm và 4cm. Kẻ đường cao ứng với cạnh huyền. Tính độ dài các đoạn thẳng mà nó chia ra trên cạnh huyền và diện tích các tam giác vuông tạo thành.

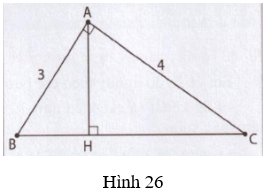
Gợi ý (h.26):

- Tính độ dài BC.

- Tính BH, CH theo công thức b² = ab’, c² = ac’

- Tính diện tích theo công thức:

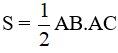
Lời giải:

* Áp dụng định lý Py-ta-go ta có:

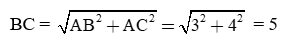
* Áp dụng công thức b² = ab', ta có:

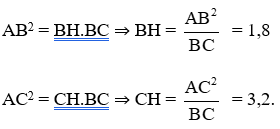
Áp dụng công thức h² = b'.c', ta có:

AH² = BH.CH ⇒ AH = 2,4

* Diện tích tam giác vuông ABC là:

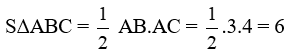
* Diện tích tam giác vuông ABH là:

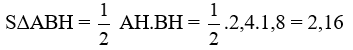
* Diện tích tam giác vuông ACH là:

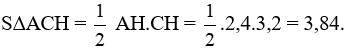
3. Cho tam giác ABC vuông tại A, phân giác AD. Biết BD = cm; CD = cm. Tính độ dài các cạnh góc vuông của tam giác (h.27)

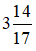
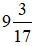
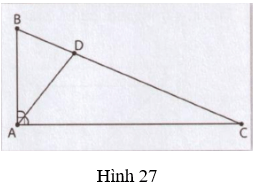
Gợi ý

- Tính độ dài BC.

- Sử dụng tính chất đường phân giác:

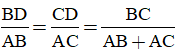
Lời giải:

Ta có:

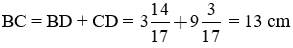
Theo tính chất đường phân giác ta có:

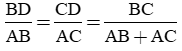
Xét:

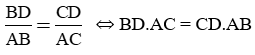
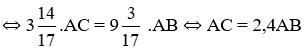
Mặt khác tam giác ABC là tam giác vuông nên:

AB² + AC² = BC²

⇔ AB² + (2,4AB)² = 13²

⇔ 6,76AB² = 169

⇔ AB = 5 cm

Suy ra AC = 12cm.

4. Cho tam giác ABC vuông tại A có BC = 10cm,

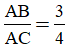
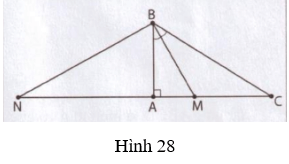
a) Tính độ dài các cạnh AB, AC

b) Các đường phân giác trong và ngoài của B cắt đường thẳng AC lần lượt tại M và N. TÍnh độ dài đoạn thẳng MN, MC.

Hướng dẫn (h.28)

b) +) Sử dụng tính chất đường phân giác để tính MA, MC.

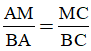
+) Chú ý rằng hai đường phân giác trong và ngoài của một góc thì vuông góc với nhau. Do đó BM ⊥ BN. Áp dụng công thức h² = b’c’ cho tam giác vuông BMN thì AB² = AM.AN.

Lời giải:

a) Theo bài ra ta có:

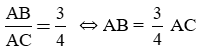
Áp dụng định lý Py-ta-go vào tam giác vuông ABC, ta có:

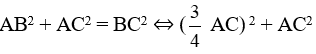
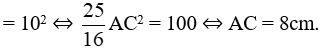
⇒ AB = 6cm.

Vậy AB = 6cm, AC = 8cm.

b) * Theo tính chất đường phân giác, ta có:

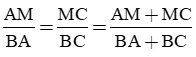
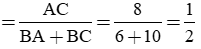
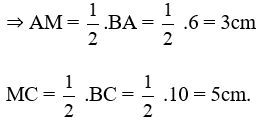
* Ta có tính chất hai đường phân giác trong và ngoài của một góc thì vuông góc với nhau, do đó BM ⊥ BN

Áp dụng công thức h² = b'.c' cho tam giác vuông BMN ta có:

AB² = AM.AN ⇒ AN = 12cm

Suy ra MN = AN + AM = 12 + 3 = 15cm

Vậy MC = 5cm, MN = 15cm.

D.E. Hoạt động vận dụng và tìm tòi, mở rộng

1. Em có biết?

Ngày 4 tháng 10 năm 1957, vệ tinh nhân tạo đầu tiên với tên gọi Sputnik 1 được Liên bang Xô viết phóng lên quỹ đạo Trái Đất. Vệ tinh viễn thông địa tĩnh đầu tiên của Việt Nam được phóng vào vũ trụ lúc 22 giờ 16 phút ngày 18 tháng 4 năm 2008 (giờ UTC) gọi là Vinasat – 1. Việt Nam đã tiến hành đàm phán với 27 quốc gia và vùng lãnh thổ để có được vị trí 132 độ Đông trên quỹ đạo địa tĩnh.

ERS 2, một vệ tinh quan sát Trái Đất của cơ quan Vũ trụ Châu Âu

Vệ tinh Vinasat – 1

Bài toán 1. Hai vệ tinh đang bay ở vị trí A và B cùng cách mặt đất 230km có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là 2200km? Biết rằng bán kính R của Trái Đát gần bằng 6370km và hai vệ tinh “nhìn” thấy nhau nếu OH > R (OH là khoảng cách từ tâm Trái Đất O đến đường thẳng nối hai vệ tinh AB).

Lời giải:

Ta có hình vẽ sau:

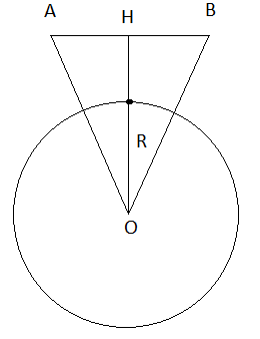
Theo bài ra, A, B cùng cách mặt đất 230km nên tam giác OAB cân tại O.

Khoảng cách AB là 2200km và bán kính Trái Đất bằng 6370km nên:

OA = OB = 230 + 6370 = 6600 km

Theo hình vẽ ta có:

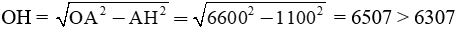
hay OH > R

Vậy hai vệ tinh A, B có thể nhìn thấy nhau.

2. Bài toán 2

Một chiếc băng tải di động có hình dạng như hình 29. Hai chân đế của băng tải có chiều cao cố định 0,8m, chân còn lại có thể được thay đổi độ cao để thuận tiện cho việc sử dụng. Biết khoảng cách giữa hai chân đế là 2m. Tính độ dài băng chuyền khi chân đế còn lại có độ cao 2m?

Lời giải:

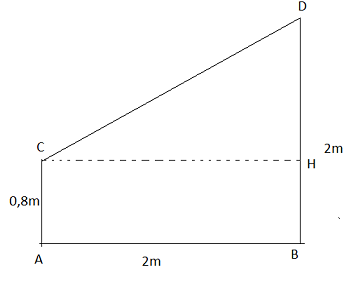
Gọi các điểm như hình vẽ

Áp dụng định lý Py-ta-go vào tam giác vuông CHD ta có:

CD² = CH² + HD²

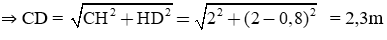
Vậy độ dài băng chuyền là 2,3m.

Xem thêm các bài Giải bài tập Toán lớp 9 chương trình VNEN hay khác:

• Bài 3: Tỉ số lượng giác của góc nhọn
• Bài 4: Sử dụng máy tính cầm tay để tính tỉ số lượng giác
• Bài 5: Một số hệ thức về cạnh và góc trong tam giác vuông
• Bài 6: Luyện tập
• Bài 7: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn

Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:

• Giải sách bài tập Toán 9
• Chuyên đề Toán 9 (có đáp án - cực hay)
• Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
• Các dạng bài tập Toán 9 cực hay
• Đề thi Toán 9
• Đề thi vào 10 môn Toán

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---