Giải Toán 9 VNEN Bài 2: Đồ thị của hàm số y = ax² (a ≠ 0)

A. Hoạt động khởi động

Quan sát và liên tưởng

Hình bên là hình ảnh một quả bóng nảy trên mặt đất được chụp lại bởi một đèn flash với tốc độ 25 hình mỗi giây. Cùng với chuyển động quay và lực cản không khí, quỹ đạo mà quả bóng vạch ra là một đường cong trông giống như một chữ U quay ngược.

Tia nước từ vòi phun lên cao rồi rơi xuống, vệt sáng của pháo hoa đều vạch ra những đường cong có hình dạng như chữ U quay ngược.

Các đường cong nói trên thường được cho là có hình dạng giống đồ thị của hàm số y = ax².

B. Hoạt động hình thành kiến thức

1. Thực hiện các hoạt động sau

a) Điền vào ô trống giá trị của y tương ứng với mỗi giá trị của x trong bảng sau:

b) Từ bảng trên, hãy viết tiếp vào chỗ chấm (…) để được tọa độ một số điểm thuộc đồ thị hàm số y = 2x² rồi xác định các điểm đó trên hệ tọa độ Oxy trong hình 6a (theo mẫu):

A(-3; 18) ; A’(3; …) ; B(-2; …) ; B’(2; …); C(-1; …); C’(1; …); O(0; …)

c) Đồ thị hàm số y = 2x² là đường cong đi qua các điểm A, A’, B,B’, C, C’, O như hình 6b.

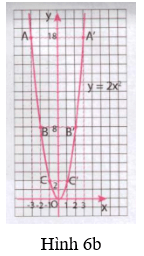
Hãy tô lại bằng bút chì đồ thị hàm số y = 2x² trong hình 6b rồi vẽ lại vào hình 6a.

d) Hãy nhận xét một vaì đặc điểm của đồ thị hàm số y = 2x² bằng cách trả lời các câu hỏi sau:

- Đồ thị nằm ở phía trên hay phía dưới trục hoàn?

- Vị trí của các điểm A, A’ đối với trục Oy? Tương tự đối với các cặp điểm B, B’ và C, C’?

- Điểm nào là điểm thấp nhất của đồ thị?

Trả lời:

a)

b) A(-3; 18); A'(3; 18); B(-2; 8); B'(2; 8); C(-1; 2); C'(1; 2); O(0; 0)

c) Các em vẽ lại hình 7b vào vở

d)

• Đồ thị nằm ở phía trên trục hoành

• Các cặp điểm A và A'; B và B'; C và C' đối xứng nhau qua trục tung.

• Điểm thấp nhất của đồ thị là điểm O

2. Thực hiện các hoạt động sau

a) Điền vào ô trống giá trị của y tương ứng với mỗi giá trị x trong bảng sau:

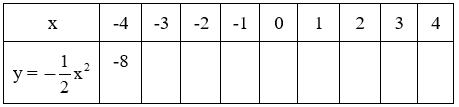
b) Từ bảng trên, hãy viết tiếp vào chỗ chấm (…) để được tọa độ một số điểm thuộc đồ thị hàm số 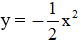rồi xác định các điểm đó trên hệ trục tọa độ trong hình 7a (theo mẫu):

M(-4 ; -8); M’(4; …); N(-2; …); N’(2; …); P(-1; …); P’(1; …); O(0; …)

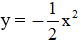
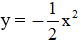
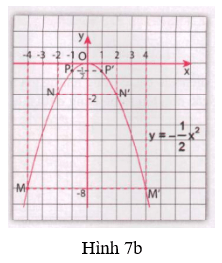
c) Đồ thị hàm số là đường cong đi qua các điểm M,M’, N, N’, P, P’, O như ở hình 7b. Hãy tô lại bằng bút chì đồ thị hàm số trong hình 7b rồi vẽ lại vào hình 7a.

d) Hãy nhận xét một vài đặc điểm của đồ thị hàm số 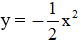bằng cách trả lời các câu hỏi sau:

- Đố thị nằm ở phía trên hay phía dưới trục hoành?

- Vị trí của các điểm M, M’đối với trục Oy? Tương tự đối với các cặp điểm N, N’ và P, P’?

- Điểm nào là điểm cao nhất của đồ thị

Trả lời:

a)

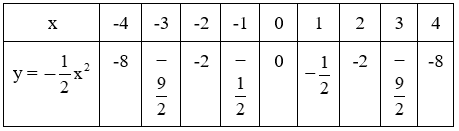
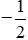
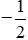
b) M(-4; -8); M'(4; 8); N(-2; -2); N'(2; -2); P(-1; ); P'(1; ); O(0; 0)

c) Các em vẽ lại hình 7b vào vở

d)

• Đồ thị nằm phía dưới trục hoành

• Các cặp điểm đó đối xứng nhau qua trục Oy

• Điểm cao nhất của đồ thị là O(0; 0)

3. Đọc kĩ nội dung sau

Đồ thị của hàm số y = ax² (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó gọi là một parabol với đỉnh O.

- Nếu a > 0 thì đồ thị đó nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

- Nếu a < 0 thì đồ thị đó nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

Cách vẽ đồ thị hàm số y = ax² (a ≠ 0)

Bước 1: Lập bảng giá trị (tọa độ của một số điểm thuộc đồ thị).

Bước 2: Biểu diễn các điểm có tọa độ được xác định trong bảng giá trị trên mặt phẳng tọa độ.

Bước 3: Vẽ parabol.

Chú ý:

- Vì đồ thị y = ax² (a ≠ 0) luôn đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị của hàm số này, ta chỉ cần tìm một số điểm của đồ thị ở bên phải trục Oy rồi lấy các điểm đối xứng với chúng qua trục Oy.

- Đồ thị minh họa một cách trực quan tính chất của hàm số. Chẳng hạn:

+ Đồ thị của hàm số y = 2x² cho thấy: Khi x âm và tăng thì đồ thị đi lên, chứng tỏ hàm số đồng biến. Khi x dương và tăng thì đồ thị đi xuống, chứng tỏ hàm số nghịch biến.

4. Thực hiện các hoạt động sau

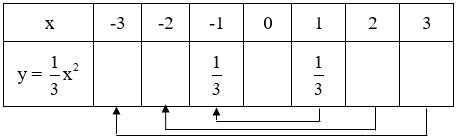
* Lập bảng giá trị của hàm số 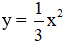ứng với x = 0; x = 1; x = 2; x = 3 vào vở rồi điền vào các ô trống những giá trị tương ứng với x = -1; x = -2; x = -3 được chi rõ bởi các mũi tên trong bảng dưới đây.

Em hãy trao đổi với bạn để giải thích tại sao lại làm được như vậy.

* Vẽ đồ thị của hàm số 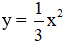vào vở.

Trả lời:

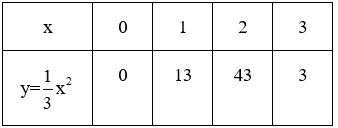
Dựa vào tính đối xứng của hàm số qua trục Oy, ta có bảng sau:

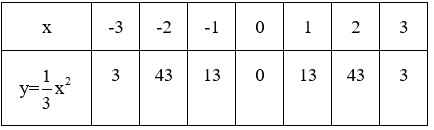
Đồ thị hàm số:

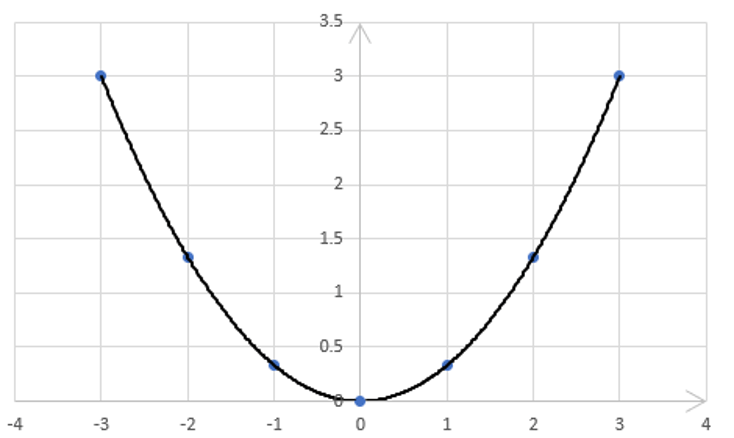
C. Hoạt động luyện tập

1. Cho hai hàm số: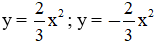

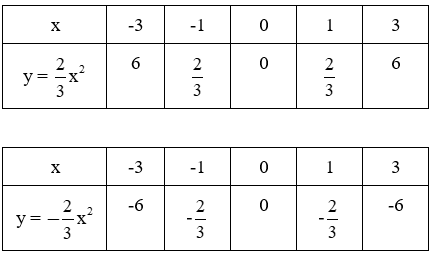
a) Hoàn thành hai bảng giá trị sau rồi vẽ hai đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ

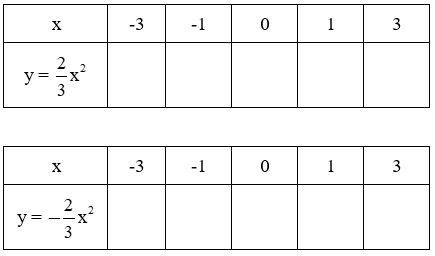
b) Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.

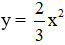
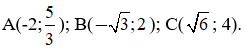
c) Trong các điểm sau đây, điểm nào thuộc đồ thị hàm số , điểm nào không thuộc đồ thị hàm số đó?

Bài làm:

a)

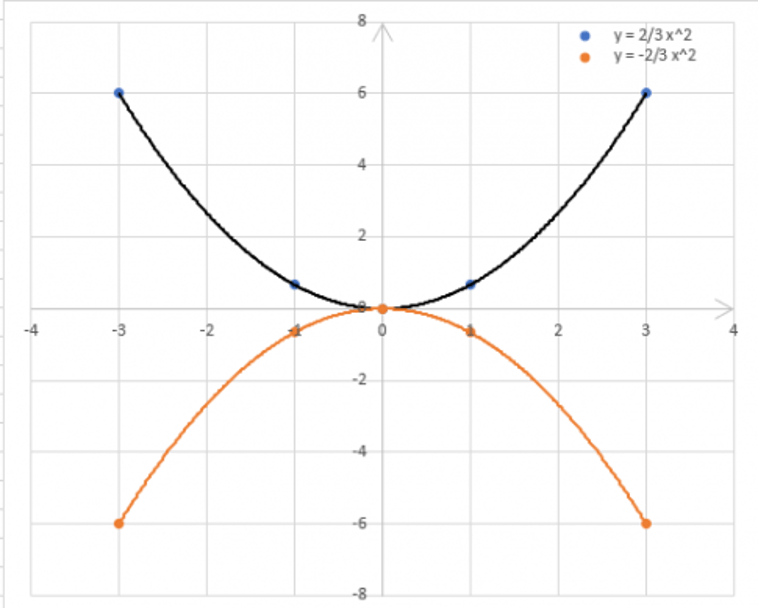
b) Đồ thị của hai hàm số trên đối xứng với nhau qua trục Ox

c) Thay tọa độ các điểm A, B, C vào phương trình hàm số:

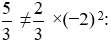
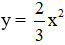
• Điểm A: Điểm A không thuộc đồ thị hàm số

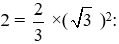
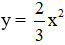
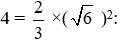
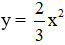
• Điểm B: Điểm B thuộc đồ thị hàm số

• Điểm C: Điểm A không thuộc đồ thị hàm số

2. Cho ba hàm số: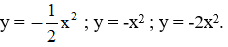

a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm trên mặt phẳng tọa độ ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị của ba hàm số đã cho. Xác định tung độ tương ứng của chúng.

c) Tìm trên mặt phẳng tọa độ điểm A’, B’, C’ có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị của ba hàm số đã cho.Kiểm tra tính đối xứng của A và A’; B và B’; C và C’.

d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị lớn nhất.

Bài làm:

a)

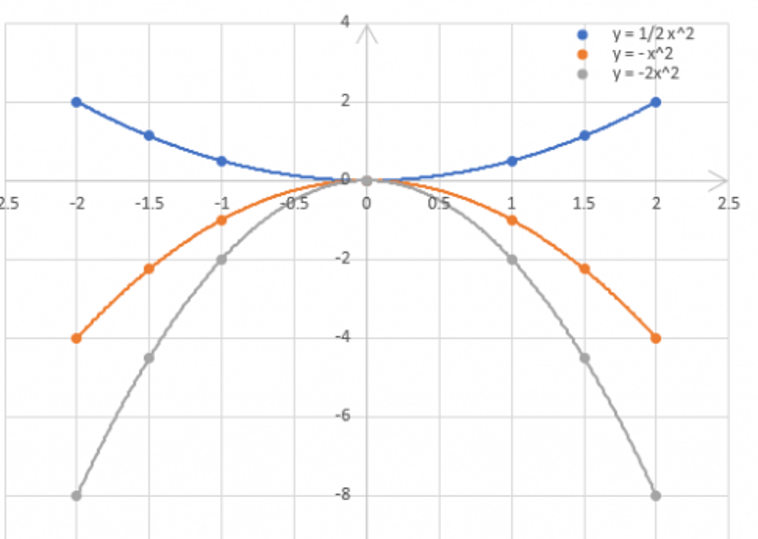
b) c)

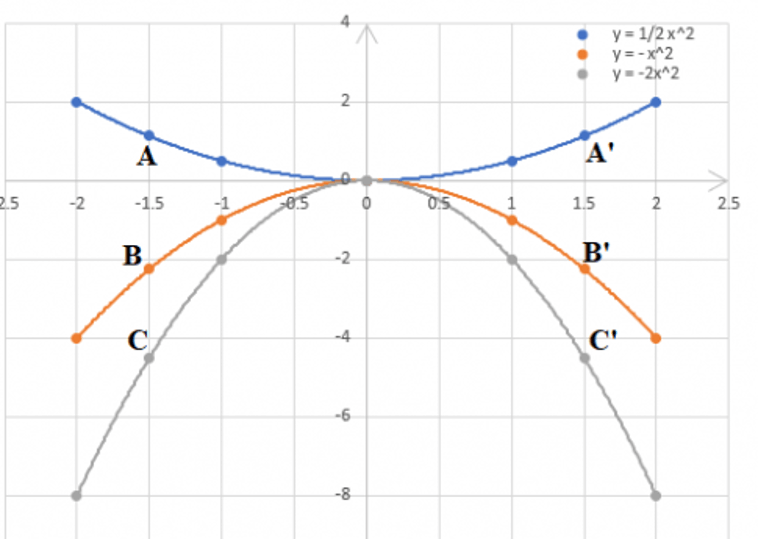
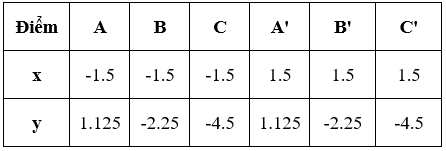
Từ bảng trên, ta thấy các điểm A và A'; B và B'; C và C' đối xứng với nhau qua trục tung.

d)

Hàm số 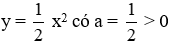nên không có giá trị lớn nhất

Hàm số y = −x²; y = −2x² có a = −1;−2 tương ứng có giá trị lớn nhất là y = 0 tại x = 0.

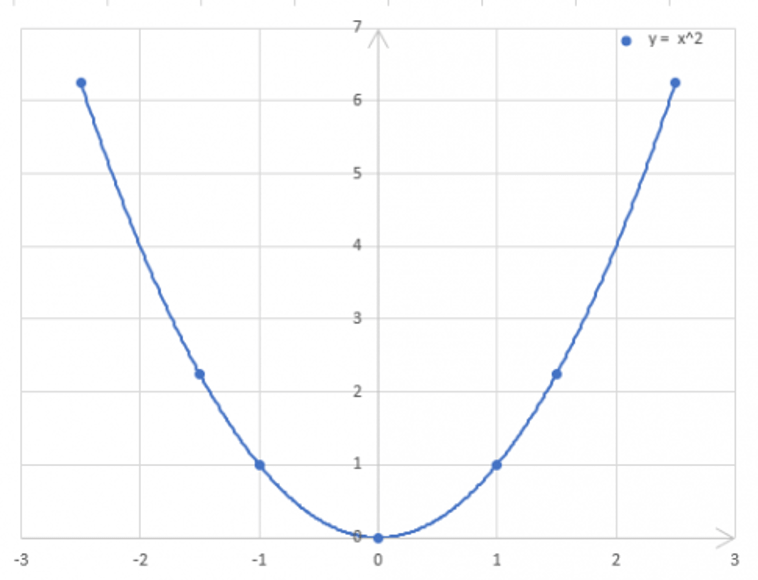
3. Cho hàm số y = f(x) = x².

a) Vẽ đồ thị hàm số đó.

b) Tính các giá trị f(-5); f(-1,2); f(0,75); f(1,5).

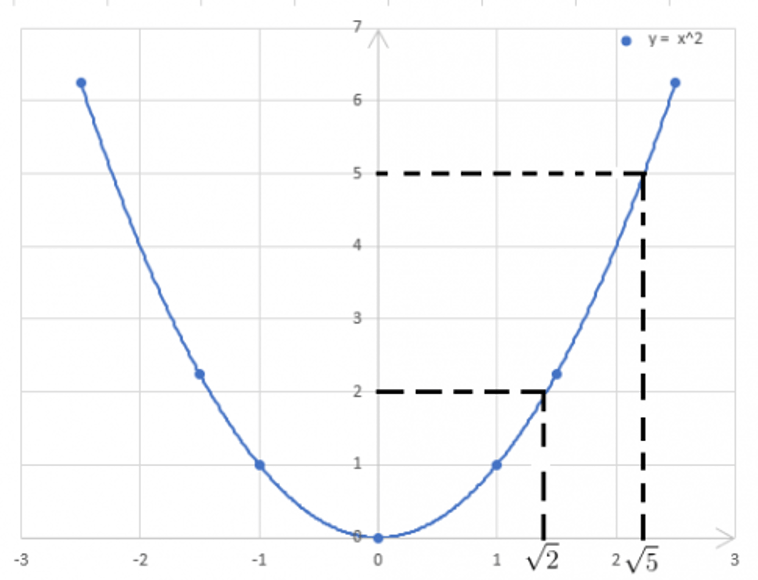
c) Dùng đồ thị hàm số trên để xác định vị trí của các điểm trên trục hoành biểu diễn các số: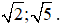

Gợi ý. Trên đồ thị hàm số, xác định các điểm có tung độ lần lượt bằng 2 và 5 rồi hạ đường vuông góc xuống trục hoành.

Bài làm:

a)

b)

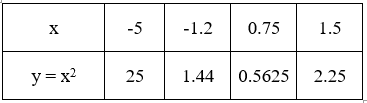
c)

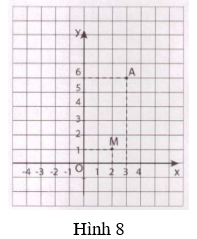
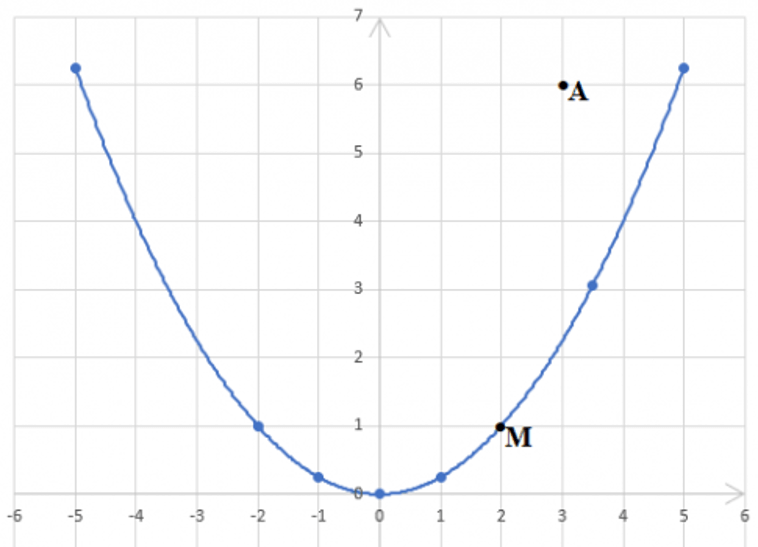
4. Trên mặt phẳng tọa độ (hình 8), có điểm M(2; 1) thuộc đồ thị của hàm số y = ax² (a ≠ 0).

a) Tìm hệ số a.

b) Điểm A(3; 6) có thuộc đồ thị hàm số trên không?

c) Hãy tìm thêm hai điểm nữa (không kể điểm O) thuộc đồ thị hàm số trên và vẽ đồ thị.

Bài làm:

a) Hàm số đi qua điểm M: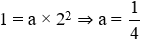

Vậy hàm số cần tìm là: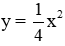

b) Thay tọa độ điểm A vào đồ thị: 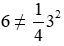. Vậy A không thuộc đồ thị hàm số

c)

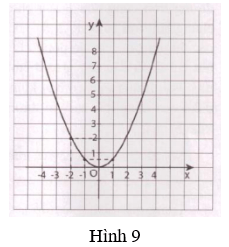
5. Biết rằng đường cong trong hình 9 là một parabol y = ax² (a ≠ 0).

a) Tìm hệ số a.

b) Tìm tung độ của điểm thuộc parabol và có hoành độ x = -3.

c) Tìm các điểm thuộc parabol có tung độ y = 8.

Bài làm:

a) Từ hình vẽ, ta có điểm (-2; 2) thuộc đồ thị.

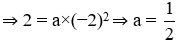
b) Tung độ của điểm có hoành độ bằng x = -3 là: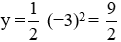

c) Hoành độ của điểm có tung độ y = 8 là: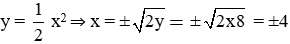

6. Cho hai hàm số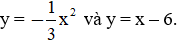

a) Vẽ đồ thị của các hàm số này trên cùng một hệ trục tọa độ.

b) Tìm tọa độ các giao điểm của hai đồ thị đó.

Bài làm:

a)

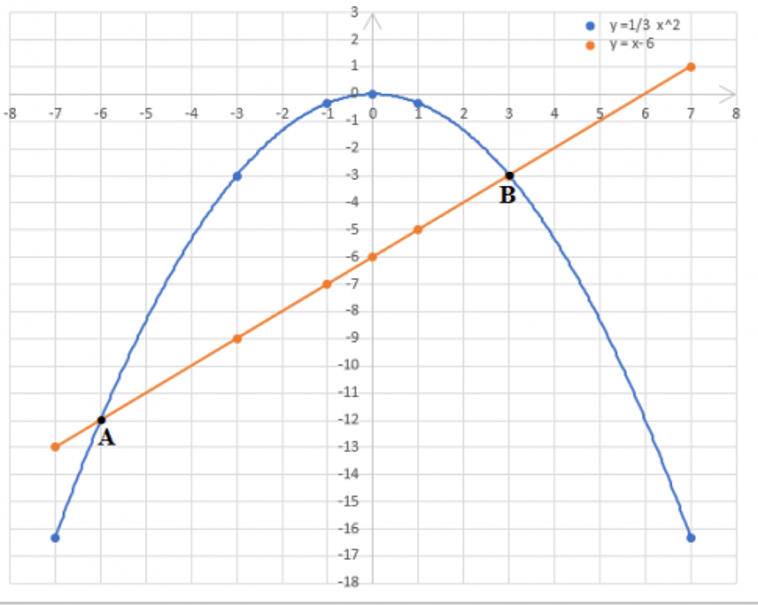
b)

Từ đồ thị: Ta thấy giao điểm của 2 đồ thị là A(-6; -12) và B(3; -3) (hình vẽ). Các tọa độ này cũng có thể thu được từ việc giải phương trình hoành độ giao điểm như sau:

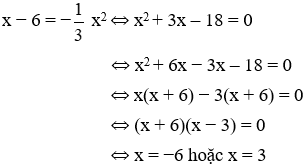
Thay hoành độ giao điểm vào phương trình đường thẳng để được tung độ các điểm:

• x = - 6; y = -12 ⇒ A(-6; -12)

• x = 3; y = -3 ⇒ B(3; -3)

D.E. Hoạt động vận dụng và tìm tòi mở rộng

1. Cho hàm số y = -0,2x².

a) Biết rằng điểm A(3; b) thuộc đồ thị hàm số, tìm b.

Hỏi điểm A’(3; b) có thuộc đồ thị hàm số không? Vì sao?

b) Biết rằng điểm C(c; -3,2) thuộc đồ thị hàm số, tìm c. Hỏi điểm C’’(c; 3,2) có thuộc đồ thị hàm số không? Vì sao?

Bài làm:

a) Thay tọa độ A vào phương trình đồ thị hàm số: b = −0.2×(−3)² = −1.8

Điểm A' đối xứng với điểm A qua trục Oy nên có thuộc đồ thị hàm số.

b) Thay tọa độ điểm C vào phương trình đồ thị hàm số: −3,2 = −0,2×c²

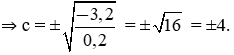
2. Cho hàm số y = ax² (a ≠ 0).

a) Tìm a, biết rằng đồ thị hàm só đi qua điểm A(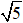 ; 3). Vẽ đồ thị hàm số với giá trị tìm được của a.

b) Biết B(-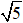 ; 3) là một điểm thuộc đồ thị nói trong câu a, O là gốc tọa độ. Tam giác AOB là tam giác gì? Vì sao?

Bài làm:

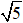
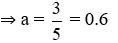
a) Thay tọa độ điểm A vào phương trình đồ thị hàm số, ta được: 3 = a×()²

Vậy phương trình đồ thị hàm số là: y = 0.6x²

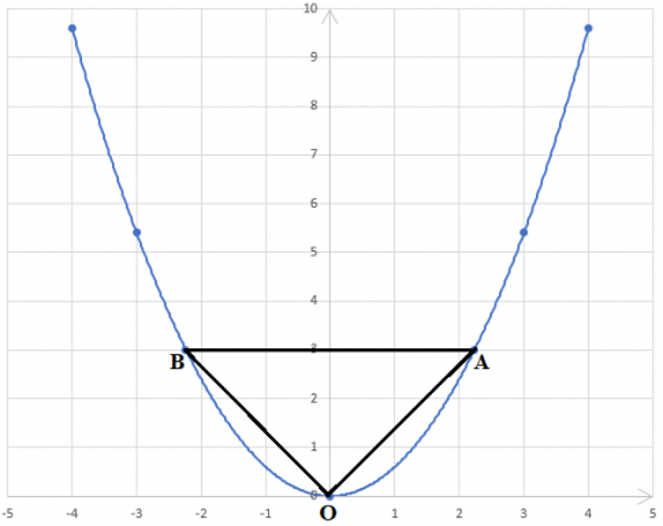
b) A và B đối xứng với nhau qua trục Oy nên OA = OB ⇒ △OAB cân tại O;

3. Giới thiệu một vài cách vẽ parabol

a) Vẽ parabol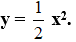

Trên trang vở có kẻ dòng, chọn khoảng cách giữa hai dòng làm đơn vị độ dài, vẽ những đường tròn cùng tâm F sao cho bán kính của chúng lần lượt bằng 1, 2, 3, … Đánh số thứ tự của các đường tròn và các dòng như hình 10. Lấy bút chì đánh dấu các giao điểm của dòng thứ nhất với đường tròn có bán kính bằng 1; giao điểm của dòng thứ hai với đường tròn có bán kính bằng 2 ; …

Nối các giao điểm này và trung điểm O của đoạn FI, ta được một parabol.

b) Vẽ parabol y = ax² (a ≠ 0), biết một điểm khác điểm O của nó.

Trong mặt phẳng tọa độ Oxy, giả sử đã biết điểm M(x₀; y₀) khác điểm O thuộc paraboly = ax². Gọi P là hình chiếu của M lên Ox. Lần lượt chia các đoạn OP, PM thành n phần bằng nhau (trong hình 11, n = 4). Qua các điểm chia đoạn OP, kẻ những đường thẳng song song với Oy. ối O với các điểm chia trên PM. Đánh số thứ tự các đường thẳng và các đoạn thẳng như trong hình 11. Lấy giao điểm của các cặp gồm một đường thẳng và một đoạn thẳng có cùng thứ tự. Nối các giao điểm này, ta được một phần của parabol. Lấy thêm hình đối xứng của phần này qua trục Oy, ta được parabol y = ax².

(Trang 37, Sách giáo khoa Toán 9 tập hai, NXB Giáo dục Việt Nam, 2016)

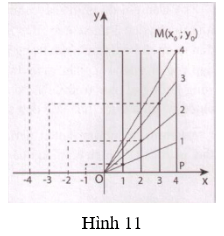
Hãy áp dụng cách vẽ này để vẽ đồ thị hàm số y = 0,6x², biết đồ thị hàm số đi qua điểm M(5; 15).

4. Em có biết?

a) Trong thực tế, chúng ta gặp rất nhiều hiện tượng, sự vật có hình dạng của parabol: đường đi của hòn đá (quả bóng) được ném (đá) đi; đường đi của tia nước từ vòi phun nước; hình ảnh cầu vồng ; các công trình kiến trúc ; …

Em hãy tìm hiểu thêm về các công trình kiến trúc có hình dạng là một parabol.

b) Các em đã nhìn thấy những anten parabol; những pha đèn ô tô; xe máy; đèn pin,… Nếu đặt bóng đèn tại một điểm thích hợp trong pha thì các tia sáng đạp vào pha đèn rồi phản xạ lại thành những tia song song hướng ra phía trước. Do đó, ánh sáng tập trung chiếu về phía trước pha làm đèn sáng hơn.

Tương tự, những anten parabol giúp cho việc thu, phát các tín hiệu có hiệu quả hơn.

Xem thêm các bài Giải bài tập Toán lớp 9 chương trình VNEN hay khác:

• Bài 1: Hàm số y = ax² (a ≠ 0)
• Bài 3: Phương trình bậc hai một ẩn
• Bài 4: Công thức nghiệm của phương trình bậc hai
• Bài 5: Luyện tập

Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:

• Giải sách bài tập Toán 9
• Chuyên đề Toán 9 (có đáp án - cực hay)
• Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
• Các dạng bài tập Toán 9 cực hay
• Đề thi Toán 9
• Đề thi vào 10 môn Toán

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

ĐỀ THI, GIÁO ÁN, SÁCH ĐỀ THI DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 9

Bộ giáo án, bài giảng powerpoint, đề thi dành cho giáo viên và sách dành cho phụ huynh tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

Tổng đài hỗ trợ đăng ký : 084 283 45 85

Giáo án, bài giảng powerpoint Văn, Toán, Lí, Hóa....

4.5 (243)

799,000đs

199,000 VNĐ

Đề thi vào 10 Toán Văn Anh của Hà Nội, Tp.Hồ Chí Minh... có lời giải

4.5 (243)

799,000đ

199,000 VNĐ

Sách Toán - Văn- Anh 6-7-8-9, luyện thi vào 10

4.5 (243)

199,000đ

99.000 - 149.000 VNĐ

xem tất cả

Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.

Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:

Loạt bài Giải bài tập Toán lớp 9 VNEN của chúng tôi được biên soạn bám sát theo chương trình Hướng dẫn học Toán 9 chương trình mới VNEN Tập 1 & Tập 2.

Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.