Giải Toán 9 VNEN Bài 6: Hệ thức Vi-et và ứng dụng

A. Hoạt động khởi động

Giải các phương trình sau

i) x² – 31x + 30 = 0

ii) 2x² + 5x + 3 = 0

- Tính tổng và tích các nghiệm của mỗi phương trình trên.

- Nhận xét về tổng và tích các nghiệm của mỗi phương trình với các hệ số của phương trình đó.

Trả lời:

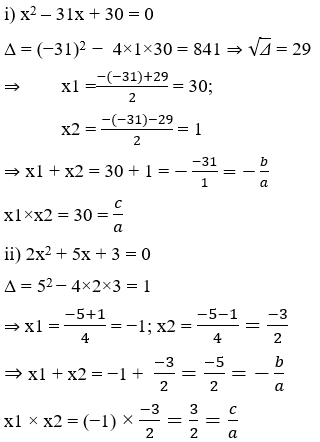
B. Hoạt động hình thành kiến thức

1. a) Thực hiện hoạt động sau

Nếu phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có nghiệm thì dù đó là hai nghiệm phân biệt hay nghiệm kép ta đều có thể viết các nghiệm đó dưới dạng:

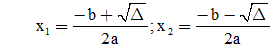
Hãy tính: x₁ + x₂ ; x₁.x₂ theo a, b, c.

b) Đọc kĩ nội dung sau

Định lí Vi-ét

Nếu x₁ , x₂ là hai nghiệm của phương trình ax² + bx + c = 0 (a ≠ 0) thì:

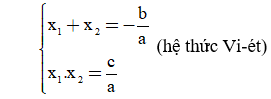
c) Biết rằng các phương trình sau có nghiệm, không giải phương trình, hãy tính tổng và tích của chún theo mẫu:

i) 2x² + 9x – 2 = 0;

ii) -3x² – 6x + 1 = 0.

Mẫu: Phương trình 4x² – 5x – 7 = 0 luôn có hai nghiệm phân biệt x₁ và x₂ (do ac = -28 < 0)

Áp dụng hệ thức Vi-ét, ta có:

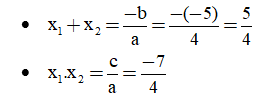
2. a) Thực hiện các hoạt động sau

Cho phương trình: 3x² – 7x + 4 = 0

 • Xác định các hệ số a, b, c rồi tính a + b + c

 • Chứng tỏ x₁ = 1 là một nghiệm của phương trình.

 • Dùng hệ thức Vi-ét để tìm x₂.

b) Đọc kĩ nội dung sau

Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm x₁ = 1, còn nghiệm kia là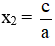

c) Tính nhẩm nghiệm của phương trình -5x² + 11x – 6 = 0 (theo mẫu):

Mẫu: Tính nhẩm nghiệm của phương trình x² – 31x + 30 = 0

Giải. Có a = 1; b = -31; c = 30 => a + b + c = 1 + (-31) + 30 = 0

Vậy phương trình đã cho có hai nghiệm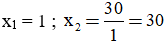

Trả lời:

a) Các hệ số: a = 3; b = -7; c = 4; a + b + c = 3 + (-7) + 4 = 0;

Thay x₁ = 1 vào vế trái phương trình: 3×1² − 7×1 + 4 = 0 = VP.

Vậy, x₁ = 1 là một nghiệm của phương trình.

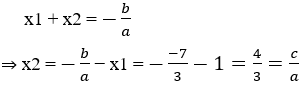
3. a) Thực hiện các hoạt động sau

Cho phương trình: x² + 7x + 6 = 0

 • Xác định các hệ số a, b, c rồi tính a - b + c

 • Chứng tỏ x₁ = -1 là một nghiệm của phương trình.

 • Dùng hệ thức Vi-ét để tìm x₂.

b) Đọc kĩ nội dung sau

Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì phương trình có một nghiệm x₁ = -1, còn nghiệm kia là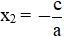

c) Tính nhẩm nghiệm của phương trình 2017x² + 2018x + 1 = 0 (theo mẫu):

Mẫu: Tính nhẩm nghiệm của phương trình 2x² + 5x + 3 = 0

Giải. Có a = 2; b = 5; c = 3 => a - b + c = 2 – 5 + 3 = 0

Vậy phương trình đã cho có hai nghiệm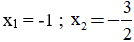

Trả lời:

a) Các hệ số: a = 1; b = 7; c = 6; a - b + c = 1 - 7 + 6 = 0;

Thay x₁ = −1 vào vế trái phương trình: ×(−1)² + 7×(−1) + 6 = 0 = VP.

Vậy, x₁ = −1 là một nghiệm của phương trình.

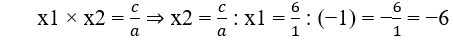
4. a) Viết tiếp vào chỗ chấm (…) để giải bài toán sau

Tìm hai số có tổng bằng S và tích bằng P.

Giải. Gọi một số là x thì số còn lại là ………

Theo giả thiết ta có phương trình x(S – x) = ……..

Hay x² – Sx + P = 0 (1)

Nếu ∆ = S² - 4P ≥ 0 thì phương trình (1) có hai nghiệm:

x₁ = …….. ; x₂ = ……….

Các nghiệm này chính là hai số cần tìm.

b) Đọc kĩ nội dung sau

Nếu hai số có tổng bảng S và tích bằng P thì hai số đó là nghiệm của phương trình: x² – Sx + P = 0

Điều kiện để có hai nghiệm đó là S² – 4P ≥ 0.

c) Viết tiếp vào chỗ chấm (…) để tìm hai số, biết tổng của chúng bằng 29 và tích của chúng bằng 198.

Giải. Hai số cần tìm là nghiệm của phương trình: x² – 29x + 198 = 0

∆ = ………………………, suy ra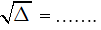

x₁ = …………. ; x₂ = ………….

Vậy hai số cần tìm là: …………….

Tương tự, hãy tìm hai số biết tổng của chúng bằng 27, tích của chúng bằng 180.

d) Viết tiếp vào chỗ chấm (…) để nhẩm nghiệm của phương trình x² + x – 6 = 0.

Giải. Vì 3 + (-2) = 1 và 3.(-2) = -6 nên x₁ = …….. ; x₂ = …… là hai nghiệm của phương trình đã cho.

Trả lời:

a) Gọi một số là x thì số còn lại là S − x

Theo giả thiết ta có phương trình: x(S − x)=P

Hay x² – Sx + P = 0

Nếu Δ = S² − 4P ≥ 0 thì (1) có hai nghiệm:

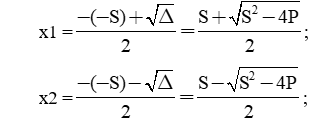
Các nghiệm này chính là hai số cần tìm.

c)

 • Hai số cần tìm là nghiệm của phương trình: x² − 29x + 198 = 0

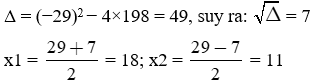
Vậy hai số cần tìm là: 18 và 11

 • Tìm hai số biết tổng của chúng bằng 27 và tích của chúng bằng 180.

Hai số cần tìm là nghiệm của phương trình: x² − 27x + 180 = 0

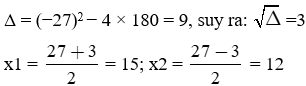
Vậy hai số cần tìm là: 15 và 12

d) Vì (−3) + 2 = −1 và (−3)×2 = −6 nên x₁ = −3; x₂ = 2 là hai nghiệm của phương trình đã cho.

C. Hoạt động luyện tập

1. Không giải phương trình, dùng hệ thức Vi-ét hãy tính tỏng và tích các nghiệm của mỗi phương trình sau (theo mẫu):

a) x² – 12x + 9 = 0;

b) 4x² – 5x – 6 = 0

c) 9x² – 6x + 1 = 0

d) 3x² – 5x – 17 = 0

Mẫu: Phương trình 2x² – 7x + 2 = 0

Ta có: ∆ = 7² – 4.2.2. = 33 > 0

Phương trình đã cho có hai nghiệm phân biệt x₁; x₂.

Theo hệ thức Vi-ét ta có:

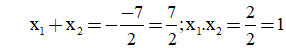
Bài làm:

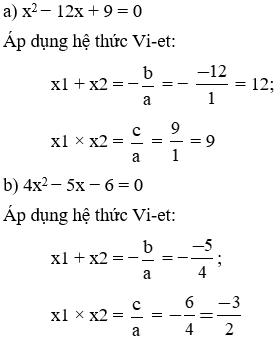
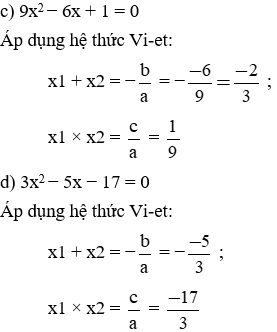
2. Dùng điều kiện a + b + c = 0 hoặc a – b + c = 0 để nhẩm nghiệm của các phương trình sau:

a) 31x² – 45x + 14 = 0

b) 7x² + 23x – 30 = 0

c) 5x² – 28x – 33 = 0

d) 1234x² + 17x – 1217 = 0

Bài làm:

a) 31x² − 45x + 14 = 0

Phương trình có: 31 + (−45) + 14 = 0 nên có hai nghiệm là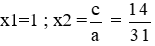

b) 7x² + 23x – 30 = 0

Phương trình có: 7 + 23 + (−30) = 0 nên có hai nghiệm là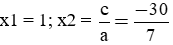

c) 5x² – 28x – 33 = 0

Phương trình có: 5 − (−28) + (−33) = 0 nên có hai nghiệm là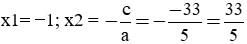

d) 1234x² + 17x – 1217 = 0

Phương trình có: 1234 − 17 + (−1217) = 0 nên có hai nghiệm là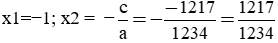

3. Dùng hệ thức Vi-ét để tính nhẩm các nghiệm của mỗi phương trình sau:

a) x² + 5x – 24 = 0

b) x² – x – 20 = 0

Bài làm:

a) x² + 5x – 24 = 0

Vì (−8) + 3 = −5 và (−8)×3 = −24 nên phương trình có hai nghiệm là: x₁ = −8 và x₂ = 3

b) x² – x – 20 = 0

Vì (−4) + 5 = 1 và (−4)×5 = −20 nên phương trình có hai nghiệm là: x₁ = −4 và x₂ = 5

4. Tìm hai số u và v trong mỗi trường hợp sau:

a) u + v = -7; uv = 12

b) u + v = 32; uv = 231

c) u + v = 3; uv = -154

Bài làm:

a) u + v = −7; u×v = 12

Hai số cần tìm là nghiệm của phương trình x² + 7x + 12 = 0

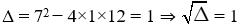
Vậy, phương trình có hai nghiệm phân biệt:

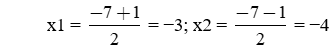
Vậy, hai số cần tìm là: −3 và −4

b) u + v = 32; u×v = 231

Hai số cần tìm là nghiệm của phương trình x² − 32x + 231 = 0

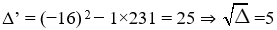
Vậy, phương trình có hai nghiệm phân biệt:

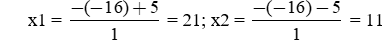
Vậy, hai số cần tìm là: 21 và 11

c) u + v = 3; u×v = −154

Hai số cần tìm là nghiệm của phương trình x² − 3x − 154 = 0

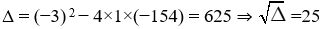
Vậy, phương trình có hai nghiệm phân biệt:

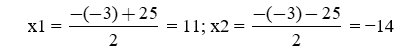
Vậy, hai số cần tìm là: 11 và −14

D.E. Hoạt động vận dụng và tìm tòi mở rộng

1. Chứng tỏ rằng phương trình 7x² – 3x – 54 = 0 có một nghiệm là 3. Tìm nghiệm còn lại.

Bài làm:

Thay x = 3 vào vế trái của phương trình: 7×(3)² − 3×3 − 54 = 0 = VP

Áp dụng hệ thức Vi-et, ta có: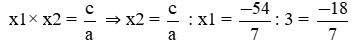

2. Lập phương trình bậc hai có hai nghiệm là hai số được cho trong mỗi trường hợp sau:

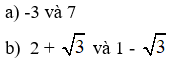
Bài làm:

a) −3 và 7

Tổng hai số đã cho là: −3 + 7 = 4.

Tích hai số đã cho là: (−3)×7 = −21

Vậy, phương trình bậc hai lập được là: x² − 4x − 21 = 0

3. Chứng tỏ rằng nếu phương trình ax² + bx + c = 0 có nghiệm x₁ và x₂ thì tam thức ax² + bx + c = a(x – x₁)(x – x₂).

Áp dụng. Phân tích đa thức thành nhân tử:

a) 2x² – 5x + 3

b) 3x² + 8x + 5

Bài làm:

 • Chứng minh:

Phương trình ax² + bx + c = 0 có nghiệm x₁ và x₂ khi Δ = b² − 4ac ≥ 0

Gọi hai nghiệm của phương trình là x₁ và x₂;

Áp dụng hệ thức Vi-et ta có: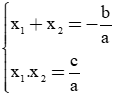

Xét tam thức:

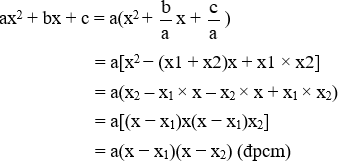
 • Áp dụng:

a) 2x² − 5x + 3 = 0

Phương trình trên có: 2 + (-5) + 3 = 0 nên có một nghiệm là

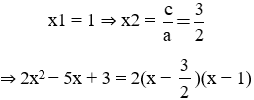
b) 3x² + 8x + 5 = 0

Phương trình trên có: 3 - 8 + 5 = 0 nên có một nghiệm là

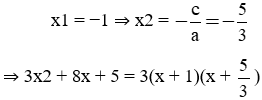
4. Em có biết?

Phrăng-xoa Vi-ét (F.Viete) sinh năm 1540 tại Pháp. Ông là một nhà toán học nổi tiếng. Chính ông là người đầu tiên dùng chữ để kí hiệu các ẩn và cả các hệ số của phương trình, đồng thời dùng chúng trong việc biến đỏi và giải phương trình. Nhờ cách dùng chữ để kí hiệu mà Đại số đã phát triển mạnh mẽ. Ông đã phát hiện mối liên hệ giữa các nghiệm và các hệ số của phương trình bậc hai.

Ngoài việc làm toán, Vi-ét còn là một luật sư và một chính trị ra nổi tiếng. Ông mất năm 1603.

(Trang 53, Sách giáo khoa toán 9 tập hai, NXB Giáo dục Việt Nam, 2016)

Xem thêm các bài Giải bài tập Toán lớp 9 chương trình VNEN hay khác:

• Bài 3: Phương trình bậc hai một ẩn
• Bài 4: Công thức nghiệm của phương trình bậc hai
• Bài 5: Luyện tập
• Bài 7: Luyện tập

Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:

• Giải sách bài tập Toán 9
• Chuyên đề Toán 9 (có đáp án - cực hay)
• Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
• Các dạng bài tập Toán 9 cực hay
• Đề thi Toán 9
• Đề thi vào 10 môn Toán

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

ĐỀ THI, GIÁO ÁN, SÁCH ĐỀ THI DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 9

Bộ giáo án, bài giảng powerpoint, đề thi dành cho giáo viên và sách dành cho phụ huynh tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

Tổng đài hỗ trợ đăng ký : 084 283 45 85

Giáo án, bài giảng powerpoint Văn, Toán, Lí, Hóa....

4.5 (243)

799,000đs

199,000 VNĐ

Đề thi vào 10 Toán Văn Anh của Hà Nội, Tp.Hồ Chí Minh... có lời giải

4.5 (243)

799,000đ

199,000 VNĐ

Sách Toán - Văn- Anh 6-7-8-9, luyện thi vào 10

4.5 (243)

199,000đ

99.000 - 149.000 VNĐ

xem tất cả

Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.

Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:

Loạt bài Giải bài tập Toán lớp 9 VNEN của chúng tôi được biên soạn bám sát theo chương trình Hướng dẫn học Toán 9 chương trình mới VNEN Tập 1 & Tập 2.

Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.