15 Bài tập trắc nghiệm Toán 10 Chương 7 Chân trời sáng tạo (có lời giải)

Đáp án đúng là: D

Xét f(x) = x² – 4 có ∆ = 16 > 0, hai nghiệm phân biệt là x = –2; x = 2 và a = 1 > 0

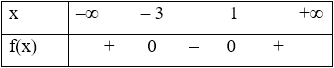
Ta có bảng xét dấu:

Từ bảng xét dấu ta có f(x) > với mọi x ∈ (–∞; –2) và (2; +∞); f(x) < 0 khi x ∈ (– 2; 2)

Vậy khẳng định sai là D.

Xét f(x) = x² + 2x – 3 có ∆ = 16 > 0, hai nghiệm phân biệt là x = 1 ; x = – 3 và a = 1 > 0.

Ta có bảng xét dấu:

Từ bảng xét dấu ta có f(x) > với mọi x ∈ (- ∞; - 3) ∪ (1; + ∞); f(x) < 0 khi x ∈ (– 3; 1).

Vậy f(x) nhận giá trị dương với mọi x ∈ (- ∞; - 3) ∪ (1; + ∞).

Đáp án đúng là: B

Bình phương hai vế của phương trình ta có

2x – 3 = (x – 3)²

⇒ 2x – 3 = x² – 6x + 9

⇒ x² – 8x + 12 = 0

⇒ x = 2 hoặc x = 6

Thay lần lượt hai nghiệm vào phương trình, ta thấy x = 6 thoả mãn

Vậy phương trình có 1 nghiệm

Đáp án đúng là: A

Bình phương hai vế của phương trình ta có

x² – 3x = 2x – 4

⇒ x² – 5x + 4 = 0

⇒ x = 1 hoặc x = 4

Thay lần lượt hai nghiệm vào phương trình, ta thấy x = 4 thoả mãn

Vậy phương trình có nghiệm là x = 4

Đáp án đúng là: A

Trường hợp 1. m = 0. Khi đó f(x) = – 2x – 1 ≤ 0 $\iff x\ge -\frac{1}{2}$

Vậy m = 0 không thỏa mãn f(x) ≤ 0 với ∀x ∈ ℝ

Trường hợp 2. m ≠ 0.

Khi đó: f(x) = mx² – 2x – 1 < 0 với ∀x ∈ ℝ $\iff \left(\begin{array}{c}a=m<0\\ {\Delta }^{\text{'}}=1+m\le 0\end{array}\right)\iff m\le -1$

Vậy m ≤ – 1 thỏa mãn bài toán.

Đáp án đúng là: C

$x^2-2x+3\sqrt{x^2-2x-3}=7\iff x^2-2x-3+3\sqrt{x^2-2x-3}-4=0$

Đặt $\sqrt{x^2-2x-3}=t$ (t ≥ 0) ta có phương trình t² + 3t – 4 = 0$\iff \left(\begin{array}{c}t=1\\ t=-4\end{array}\right)$

Kết hợp với điều kiện của t ta có t = 1 thỏa mãn

Với t = 1 $\Rightarrow \sqrt{x^2-2x-3}=1\iff x^2-2x-4=0\iff \left(\begin{array}{c}x=1+\sqrt{5}\\ x=1-\sqrt{5}\end{array}\right)$

Thay lần lượt các nghiệm vào phương trình ta có $x=1+\sqrt{5};x=1-\sqrt{5}$ đều thỏa mãn

Vậy tích các nghiệm của phương trình S = – 4.

Đáp án đúng là: C

Bình phương hai vế của phương trình đã cho ta có

x – 2 + x + 3 + 2$\sqrt{(x-2)(x+3)}$ = 25

⇒ $\sqrt{x^2+x-6}$ = 12 – x(1)

Bình phương hai vế của phương trình (1) ta có

x² + x – 6 = (12 – x)²

⇒ x² + x – 6 = x² – 24x + 144

⇒ 25x – 150 = 0

⇒ x = 6

Thay nghiệm trên vào phương trình ta thấy x = 6 thoả mãn

Vậy nghiệm của phương trình thuộc khoảng (3; 7)

Đáp án đúng là: A

Xét f(x) = 2x² – 7x – 15 có ∆ = 169 > 0, hai nghiệm phân biệt là x = 5; x = $-\frac{3}{2}$ và a = 2 > 0

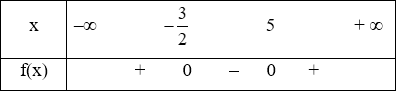
Ta có bảng xét dấu:

Từ bảng xét dấu ta có f(x) không âm khi x ∈ $\left(-\infty ;-\frac{3}{2}\right)\cup \left(5;+\infty \right)$.

Đáp án đúng là: B

Ta có (m² + 2)x² – 2(m – 2)x + 2 > 0 với mọi x ∈ ℝ $\iff \left(\begin{array}{c}a>0\\ {\Delta }^{/}<0\end{array}\right)$$\iff \left(\begin{array}{c}{m}^2+2>0\\ -m^2-4m<0\end{array}\right)$

Ta có m² + 2 > 0 với mọi m nên để (m² + 2)x² – 2(m – 2)x + 2 > 0 với mọi x ∈ ℝ thì – m² – 4m < 0

Xét f(m) = – m² – 4m có ∆ = 16 > 0, hai nghiệm phân biệt là m = 0; m = – 4 và a = – 1 < 0

Ta có bảng xét dấu:

Vậy để f(m) < 0 khi m < – 4 hoặc m > 0.

Đáp án đúng là: B

Ta có x² + 3mx² + 4mx + 4 ≥ 0

⇔ (1 + 3m)x² + 4mx + 4 ≥ 0

Với 1 + 3m = 0 thì m = $-\frac{1}{3}$ thì bất phương trình trở thành ⇔ x + 4 ≥ 0 ⇔ x ≤ 3. Vậy m = $-\frac{1}{3}$ không thỏa mãn.

Với 1 + 3m ≠ 0 thì m ≠ $-\frac{1}{3}$

Để bất phương trình (1 + 3m)x² + 4mx + 4 ≥ 0 với mọi x ∈ ℝ thì

$\iff \left(\begin{array}{c}1+3m>0\\ \Delta \text{'}=4m^2-12m-4\le 0\end{array}\right)$$\iff \left(\begin{array}{c}m>-\frac{1}{3}\\ 4m^2-12m-4\le 0\end{array}\right)$

Xét f(m) = 4m² – 12m – 4 có ∆ = 208 > 0, hai nghiệm phân biệt là x = $\iff \left(\begin{array}{c}m>-\frac{1}{3}\\ 4m^2-12m-4\le 0\end{array}\right)$ ; x = $\frac{3+\sqrt{13}}{2}$ và a = 4 > 0

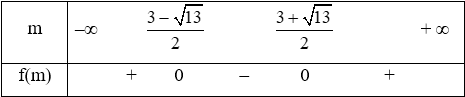
Ta có bảng xét dấu:

Từ bảng xét dấu ta có để f(m) ≤ 0 thì $\frac{3-\sqrt{13}}{2}$ ≤ m ≤ $\frac{3+\sqrt{13}}{2}$

Kết hợp với điều kiện của m để (1 + 3m)x² + 4mx + 4 ≥ 0 với mọi x ∈ ℝ thì $\frac{3-\sqrt{13}}{2}$ ≤ m ≤ $\frac{3+\sqrt{13}}{2}$

Vậy có 4 giá trị nguyên của m để bất phương trình (1 + 3m)x² + 4mx + 4 ≥ 0 với mọi x ∈ ℝ.

Đáp án đúng là: C

Để bất phương trình x² + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x ∈ ℝ thì $\left(\begin{array}{c}a=1>0\\ \Delta \text{'}<0\end{array}\right)$$\iff \left(\begin{array}{c}a=1>0\\ {\text{(m - 2)}}^{\text{2}}-2m+1<0\end{array}\right)$$\iff \left(\begin{array}{c}a=1>0\\ m^2-6m+5<0\end{array}\right)$

Xét f(m) = m² – 6m + 5 có ∆ = 16 > 0 hai nghiệm phân biệt là m = 1 ; m = 5 và a = 1 > 0

Ta có bảng xét dấu:

Suy ra để f(m) < 0 thì 1 < m < 5.

Vậy với 1 < m < 5 thì bất phương trình x² + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x ∈ ℝ.

Đáp án đúng là: C

Ta có 4x² – 12x + 5$\sqrt{4x^2-12x}$ = 0

Đặt $\sqrt{4x^2-12x}$ = t (t ≥ 0)

Phương trình (1) trở thành t² + 5t = 0 $\iff \left(\begin{array}{c}t=0\\ t=-5\end{array}\right)$

Kết hợp với điều kiện t = 0 thoả mãn

Với t = 0 ta có $\sqrt{4x^2-12x}$ = 0

⇒ 4x² – 12x = 0

⇒ x = 0 hoặc x = 3

Thay lần lượt các nghiệm trên vào phương trình, ta thấy x = 0 và x = 3 thoả mãn.

Vậy phương trình có hai nghiệm.

Đáp án đúng là: B

Ta có x² + 2$\sqrt{x^2-3x+11}$ = 3x + 4 ⇔ x² – 3x + 11 + 2$\sqrt{x^2-3x+11}$ – 15 = 0

Đặt $\sqrt{x^2-3x+11}$ = t (t ≥ 0)

Phương trình trở thành t² + 2t – 15 = 0 <![if !vml]><![endif]>

Kết hợp với điều kiện t = 3 thoả mãn

Với t = 3 ta có $\sqrt{x^2-3x+11}$ = 3

⇒ x² – 3x + 11 = 9

⇒ x² – 3x + 2 = 0

⇒ x = 2 hoặc x = 1

Thay lần lượt các nghiệm trên vào phương trình, ta thấy x = 1 và x = 2 thoả mãn

Tích các nghiệm của phương trình là 1.2 = 2

Đáp án đúng là: C

Đặt $\sqrt{x+3}+\sqrt{6-x}=t$ (t > 0) ⇔ x + 3 + 6 – x + $2\sqrt{(x+3)(6-x)}$ = t²

Ta có $\sqrt{(x+3)(6-x)}=\frac{t^2-9}{2}$

Phương trình (*) trở thành t = 3 + $\frac{t^2-9}{2}$

⇒ t² – 2t – 3 = 0

⇒ t = – 1 hặc t = 3

Kết hợp với điều kiện t = 3 thoả mãn

Với t = 3 ta có $\sqrt{x+3}+\sqrt{6-x}=3$

⇒ x + 3 + 6 – x + $2\sqrt{(x+3)(6-x)}$ = 9

⇒ $\sqrt{(x+3)(6-x)}$ = 0

⇒ – x² + 3x + 18 = 0

⇒ x = 6 hoặc x = – 3

Thay lần lượt các nghiệm trên vào phương trình, ta thấy x = 6 và x = – 3 thoả mãn

Tổng các nghiệm của phương trình là 6 + (– 3) = 3.

Đáp án đúng là: C

$\sqrt{3x-2}+\sqrt{x-1}=4x-9+2\sqrt{3x^2-5x+2}$ (*)

Đặt $\sqrt{3x-2}+\sqrt{x-1}=t(t>0)$

⇔ 3x – 2 + x – 1 + 2$\sqrt{3x^2-5x+2}$ = t²

⇔ 4x – 3 + 2$\sqrt{3x^2-5x+2}$ = t²

⇔ 4x – 9 + 2$\sqrt{3x^2-5x+2}$ = t² – 6

Phương trình (*) trở thành t = t² – 6

⇒ t² – t – 6 = 0

⇒ t = 3 hoặc t = – 2.

Kết hợp với điều kiện t = 3 thoả mãn

Với t = 3 ta có $\sqrt{3x-2}+\sqrt{x-1}=3$

⇒ 4x – 3 + 2<![if !vml]><![endif]>= 9

⇒ $\sqrt{3x^2-5x+2}$ = – 2x + 6

⇒ 3x² – 5x + 2 = (6 – 2x)²

⇒ 3x² – 5x + 2 = 4x² – 24x + 36

⇒ x² – 19x + 34 = 0

⇒ x₁ = 17 hoặc x₂ = 2

Thay lần lượt các nghiệm trên vào phương trình (*), ta thấy x₂ = 2 thoả mãn

Giá trị của biểu thức A = 2² – 3.2 + 15 = 13.