18 Bài tập Tích vô hướng của hai vectơ (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 10
Với 18 bài tập trắc nghiệm Tích vô hướng của hai vectơ Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ, có đúng sai, trả lời ngắn sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
18 Bài tập Tích vô hướng của hai vectơ (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 10
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Câu 1. Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
A. và .
B. và .
C. và .
D. và .
Câu 2. Góc giữa vectơ và vecto có số đo bằng:
A. 90°.
B. 0°.
C. 135°.
D. 45°.
Câu 3. Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?
A.
B. và
C.
D.
Câu 4. Khi nào thì hai vectơ và vuông góc?
A. . = 1;
B. . = - 1;
C. . = 0;
D. a.b = -1.
Câu 5. Trong mặt phẳng tọa độ Oxy, cho điểm A(-1; 3), B(0; 4) và C(2x – 1; 3x2). Tổng các giá trị của x thỏa mãn
A. ;
B. ;
C. ;
D. 1.
Câu 6. Khi nào tích vô hướng của hai vecto là một số dương.
A. Khi góc giữa hai vectơ là một góc tù;
B. Khi góc giữa hai vectơ là góc bẹt;
C. Khi và chỉ khi góc giữa hai vectơ bằng 00;
D. Khi góc giữa hai vectơ là góc nhọn hoặc bằng 00.
Câu 7. Khi nào thì
A. = 0;
B. Góc giữa hai vecto là 0° hoặc 180°;
C. = 1;
D. Góc giữa hai vecto là 90°.
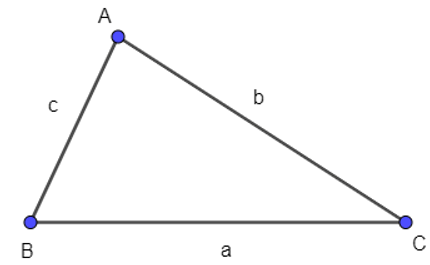
Câu 8. Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính theo a, b, c.
A. ;
B. ;
C. ;
D.
Câu 9. Tính tích vô hướng của hai vectơ là k. Nhận xét nào sau đây đúng về giá trị của k.
A. k chia hết cho 2;
B. k là một số hữu tỉ;
C. k là một số nguyên dương;
D. k là một số vô tỉ.
Câu 10. Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vecto và trong trường hợp .
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Câu 11. Cho đoạn thẳng AB và điểm I là trung điểm của đoạn thẳng AB. Với điểm M bất kì, khẳng định nào dưới đây là đúng?
A. MI2 + IA2;
B. MI2 + 2 IA2;
C. MI2 – IA2;
D. 2MI2 + IA2.
Câu 12. Cho tam giác ABC với A(-1;2), B(8;-1), C(8;8). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
A. 11,4;
B. 6,7;
C. 5,7;
D. 9.
Câu 13. Tìm điều kiện của để
A. là hai vectơ ngược hướng;
B. là hai vectơ cùng hướng;
C. là hai vectơ vuông góc;
D. là hai vectơ trùng nhau.
Câu 14. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; -3), B(5; 2). Tìm điểm M thuộc tia Oy để góc
A. ;
B. ;
C. ;
D. .
Câu 15. Cho tam giác ABC có trọng tâm G. Với điểm M bất kì, đẳng thức nào sau đây đúng?
A. MA2 + MB2 + MC2 = 3MG2 + GA2 + GB2 + GC2;
B. MA2 + MB2 + MC2 = 3MG2;
C. MA2 + MB2 + MC2 = 3MG2 + (GA + GB + GC)2;
D. MA2 + MB2 + MC2 = 0.
Câu 16. Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(-3;1), B(2;4), C(2;-2). Gọi H(x; y) là trực tâm của tam giác ABC. Tính S = 5x + y.
A. ;
B. ;
C. 2;
D. 6.
Phần II. Trắc nghiệm đúng, sai
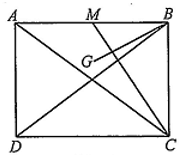
Câu hỏi. Cho hình chữ nhật . Gọi là trung điểm của là trọng tâm tam giác .
a).
b)
c).
d)
Phần III. Trắc nghiệm trả lời ngắn
Câu 1. Cho hai vectơ và . Biết và .
Tính (kết quả làm tròn đến hàng phần chục).
Câu 2. Cho tam giác vuông tại có . Gọi là trung điểm của Tính giá trị của biểu thức
Xem thêm bài tập trắc nghiệm Toán lớp 10 Kết nối tri thức có đáp án hay khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Kết nối tri thức
- Giải Chuyên đề học tập Toán 10 Kết nối tri thức
- Giải SBT Toán 10 Kết nối tri thức
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 10 (hay nhất) - KNTT
- Soạn văn 10 (ngắn nhất) - KNTT
- Soạn văn 10 (siêu ngắn) - KNTT
- Giải sgk Toán 10 - KNTT
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - KNTT
- Giải sgk Hóa học 10 - KNTT
- Giải sgk Sinh học 10 - KNTT
- Giải sgk Địa lí 10 - KNTT
- Giải sgk Lịch sử 10 - KNTT
- Giải sgk Kinh tế và Pháp luật 10 - KNTT
- Giải sgk Tin học 10 - KNTT
- Giải sgk Công nghệ 10 - KNTT
- Giải sgk Hoạt động trải nghiệm 10 - KNTT
- Giải sgk Giáo dục quốc phòng 10 - KNTT

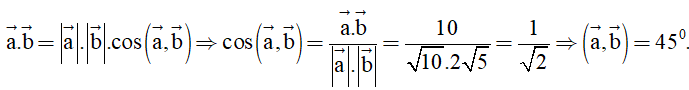



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

