Công thức tính số chỉnh hợp lớp 10 (hay, chi tiết)
Bài viết Công thức tính số chỉnh hợp lớp 10 trình bày đầy đủ công thức, ví dụ minh họa có lời giải chi tiết và các bài tập tự luyện giúp học sinh nắm vững kiến thức trọng tâm về Công thức tính số chỉnh hợp từ đó học tốt môn Toán.
Công thức tính số chỉnh hợp lớp 10 (hay, chi tiết)
1. Công thức tính số chỉnh hợp
Cho tập hợp A gồm n phần tử và một số nguyên k với 1 k n.
Kết quả của việc lấy k phần tử từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Kí hiệu là số các chỉnh hợp chập k của n phần tử (1 £ k £ n).
Ta có:
2. Ví dụ minh họa tính số chỉnh hợp
Ví dụ 1. Rút gọn:
Hướng dẫn giải:
Ví dụ 2. Một nhà hàng có 10 món đặc sản. Mỗi ngày nhà hàng đó chọn ra 2 món ăn khác nhau, trưa 1 món, tối 1 món. Hỏi nhà hàng đó có bao nhiêu cách chọn?
Hướng dẫn giải:
Số cách chọn 2 món khác nhau từ 10 món là: cách chọn.
Ví dụ 3. Một đội bóng có 22 cầu thủ, cần chọn ra 11 cầu thủ thi đấu chính thức. Hỏi có bao nhiêu cách chọn nếu:
a) Ai cũng có thể chơi ở bất kì vị trí nào?
b) Chỉ có cầu thủ A làm thủ môn còn các cầu thủ khác chơi ở vị trí nào cũng được?
Hướng dẫn giải:
a) Số cách chọn 11 cầu thủ trong 22 cầu thủ ra sân thi đấu là .
b) Số cách chọn 11 cầu thủ trong đó cầu thủ A làm thủ môn còn các cầu thủ khác vào vị trí nào cũng được là: .
Ví dụ 4. Có thể lập được bao nhiêu vectơ từ các đỉnh của hình ngũ giác đều?
Hướng dẫn giải:
Hình ngũ giác đều có tất cả 5 đỉnh. Cứ 2 đỉnh bất kì cho ta 2 vectơ. Nên số vectơ tạo từ các đỉnh của hình ngũ giác là vectơ.
Ví dụ 5. Cho các số tự nhiên 0, 1, 2, 3, 4, 5, 6, 7.
a) Lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau?
b) Bao nhiêu số tự nhiên chẵn có 3 chữ số khác nhau?
Hướng dẫn giải:
a) Số có 4 chữ số khác nhau được thành lập từ các chữ số trên là: số.
Số có dạng (a, b, c) khác nhau được thành lập từ các chữ số trên là: số.
Vậy số tự nhiên chẵn có 3 chữ số khác nhau được thành lập từ các số trên là: số.
b) Số số có 3 chữ số được thành lập từ các chữ số trên là: số.
Gọi số cần lập là số lẻ. Khi đó c có cách chọn, a có 6 cách chọn, b có 6 cách chọn. Vậy số lẻ được thành lập từ các chữ số trên là: 4.6.6 = 144 số.
Vậy số tự nhiên chẵn có 3 chữ số khác nhau được thành lập từ các số trên là:
294 – 144 = 150 số.
3. Bài tập tự luyện tính số chỉnh hợp
Bài 1. Một tổ có 10 học sinh. Hỏi có bao nhiêu cách chọn ra 2 học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó?
Bài 2. Trong trận chung kết bóng đá phải phân định thắng thua bằng đá luân lưu 11 mét. Huấn luyện viên của mỗi đội cần trình với trọng tài một danh sách sắp thứ tự 5 cầu thủ trong 11 cầu thủ để đá luân lưu 5 quả 11 mét. Hỏi huấn luyện viên của mỗi đội sẽ có bao nhiêu cách chọn?
Bài 3. Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD?
Bài 4. Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau?
Bài 5. Từ các chữ số 0, 1, 2, 3, 5 có thể lập được bao nhiêu số tự nhiên không chia hết cho 5, gồm 4 chữ số khác nhau?
Bài 6. Cho tập hợp A = {0; 1; 2; 3; 4; 5}. Có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau và lớn hơn 350?
Bài 7. Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau, sao cho trong mỗi số đó nhất thiết phải có mặt chữ số 0?
Bài 8. Có bao nhiêu số tự nhiên có bẩy chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?
Xem thêm các bài viết về công thức Toán hay, chi tiết khác:
- Quy tắc cộng
- Quy tắc nhân
- Công thức tính số hoán vị
- Công thức tính số tổ hợp
- Công thức khai triển nhị thức Newton
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài 500 Công thức, Định Lí, Định nghĩa Toán, Vật Lí, Hóa học, Sinh học được biên soạn bám sát nội dung chương trình học các cấp.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

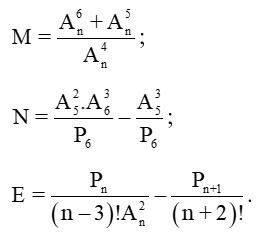






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

