Sách bài tập Toán 7 Bài 6: Tam giác cân

Sách bài tập Toán 7 Bài 6: Tam giác cân

Bài 67 trang 147 sách bài tập Toán 7 Tập 1: a, Tính góc ở đáy của một tam giác cân biết góc ở đỉnh bằng 50^o,bằng a^o.

b, Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng 50^o,bằng a^o

Lời giải:

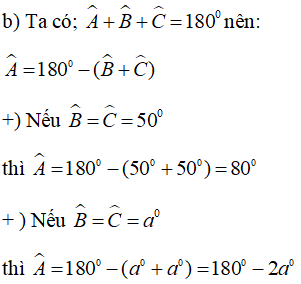
Bài 68 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A có ∠A= 100°. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Chứng minh rằng MN // BC

Lời giải:

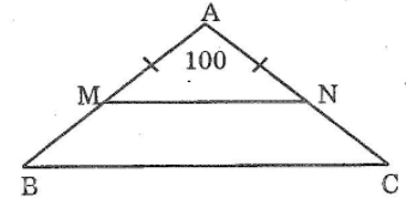
Tổng ba góc trong một tam giác bằng 180^o nên:

Bài 69 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB.

Chứng minh rằng BM = CN

Lời giải:

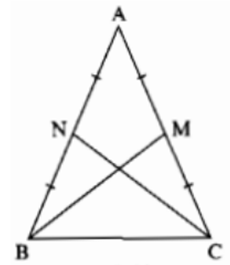
+) Do M là trung điểm của AC nên: 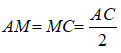(1)

+) Do N là trung điểm của AB nên: 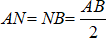(2)

Lại có: AB = AC ( vì tam giác ABC cân tại A). (3)

Từ (1); (2); (3) suy ra: AN = NB = AM = MC.

+) Xét ∆ AMB và ∆ANC có:

Góc A chung

AM = AN ( chứng minh trên)

AB = AC ( vì tam giác ABC cân tại A)

Suy ra: ∆ AMB = ∆ANC ( c.g.c)

Do đó: BM = CN ( hai cạnh tương ứng).

Bài 70 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK.

Chứng minh rằng ΔOBClà tam giác cân.

Lời giải:

+) Xét ΔABH và ΔACK, ta có:

AB = AC ( vì tam giác ABC cân tại A)

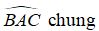
AH = AK (giả thiết)

Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.

Bài 71 trang 147 sách bài tập Toán 7 Tập 1: Vẽ lại hình bên vào vở rồi đặt bài toán vẽ tam giác để có hình bên.

Lời giải:

- Vẽ tam giác ABC vuông cân tại A

- Vẽ tam giác đều ABD sao cho D và C nằm trên 2 nửa mặt phẳng có bờ chứa đường thẳng AB.

- Vẽ tam giác vuông cân ADE sao cho E và B nằm trên 2 nửa mặt phẳng đối bờ chứa đường thẳng AD.

Chứng minh tam giác ACE là tam giác cân.

Bài 72 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng ΔADE là tam giác cân.

Lời giải:

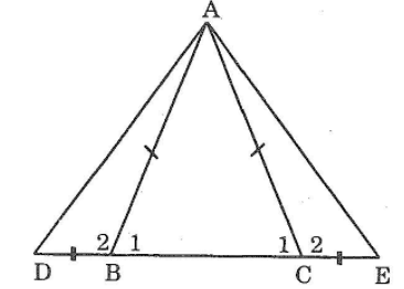
*) Ta có: ΔABC cân tại A

BD = CE (giả thiết)

Suy ra: ΔABD = ΔACE (c.g.c)

⇒ AD = AE ( hai cạnh tương ứng)

*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)

Bài 73 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Tia phân giác của góc B cắt AC ở D. trên tia đối của tia BA lấy E sao cho BE = BC. Chứng minh rằng BD // EC

Lời giải:

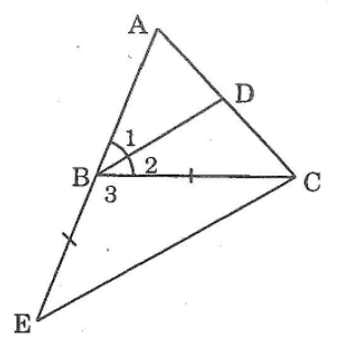
Ta có: BD là tia phân giác của ∠ABC (giả thiết)

Suy ra: 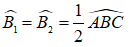(1)

Lại có: BE = BC (giả thiết)

=>∆BEC cân tại B (theo định nghĩa)

Suy ra: ∠E= ∠BCE (tính chất tam giác cân)

∆BEC có ABC là góc ngoài đỉnh B

=>∠ABC= ∠E + ∠BCE (tính chất góc ngoài tam giác)

Suy ra: ∠ABC=2∠E

Hay ∠E = (1/2)∠ABC (2)

Từ (1) và (2) suy ra: ∠E = ∠B₁ = (1/2)∠ABC

Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)

Bài 74 trang 147 sách bài tập Toán 7 Tập 1: Tính số đo các góc của tam giác ACD như hình bên.

Lời giải:

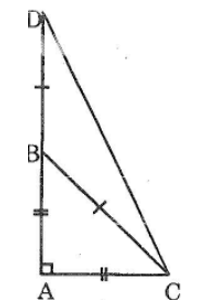
Ta có: ∆ABC vuông cân tại A

Suy ra: ∠ACB=∠ABC=45^o

Lại có: ∆BCD vuông cân tại B (BC = BD)

Suy ra: ∠BCD=∠Dtính chất tam giác cân)

Trong ∆BCD ta có ∠ABC góc ngoài tại đỉnh B

Do vậy: ∠ABC=∠BCD + ∠D (tính chất góc ngoài của tam giác)

Suy ra: ∠ABC= ∠2∠BCD

Do đó: ∠BCD = 1/2 . ∠ABC = 1/2. 45º= 22º30’

=> ∠ACD = ∠ACB + ∠BCD = 45^o+22^o30'=67^o30'

Bài 75 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Tính số đo góc BCD

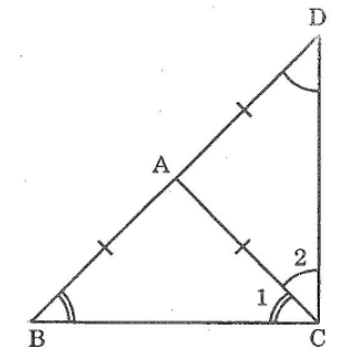
Lời giải:

Ta có: ∆ABC cân tại A

⇒ AB = AC và ∠B = ∠C₁ (tính chất tam giác cân) (1)

Lại có: AD = AB ( do A là trung điểm BD).

Suy ra: AD = AC do đó ∆ACD cân tại A

Nên ∠D =∠C₂(tính chất tam giác cân) (2)

Mà ∠BCD =∠C₁+ ∠C₂ (3)

Từ (1); (2) và (3) suy ra: ∠BCD =∠B +∠D (4)

Trong ∆BCD, ta có:

∠BCD +∠B +∠D =180^o (tổng 3 góc trong tam giác) (5)

từ (4) và (5) suy ra : 2 ∠BCD =180° hay∠BCD =90°

Bài 76 trang 147 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A có cạnh bên bằng 3cm. Gọi D là một điểm thuộc đáy BC. Qua D, kẻ cac đường thẳng song song vói các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E.

Tính tổng DE + DF

Lời giải:

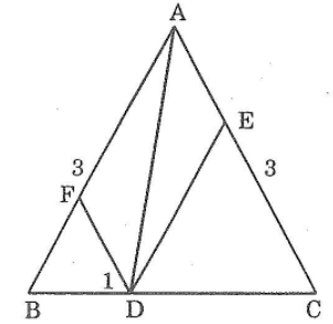
Ta có: DF // AC(gt)

=> ∠D₁ = ∠C (hai góc đồng vị) (1)

Lại có: ΔABC cân tại A

=> ∠B = ∠C (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: ∠B = ∠D₁

Hay ΔBFD cân tại F =>BF = DF (3)

Nối AD. Xét ΔAFD và ΔDEA có:

∠ADF =∠EAD(so le trong vì DF // AC)

AD cạnh chung

∠DAF =∠ADE (so le trong vì DE // AB)

Suy ra: ΔAFD= ΔDEA(g.c.g)

Nên AF = DE (hai cạnh tương ứng) (4)

Từ(3) và (4) suy ra: DE + DF = AF + BF = AB = 3cm

Bài 77 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác đều ABC. Lấy các điểm D, E , F theo thứ tự thuộc các cạnh AB, BC và CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều?

Lời giải:

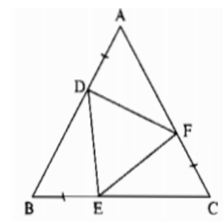
Ta có: AB = AD +DB (1)

BC = BE + EC (2)

AC = AF + FC (3)

AB = AC = BC ( vì tam giác ABC là tam giác đều) (4)

AD = BE = CF ( giả thiết) (5)

Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF

Xét ΔADF và ΔBED, ta có:

AD = BE (gt)

∠A =∠B =60^o (vì tam giác ABC đều)

AF = BD (chứng minh trên)

suy ra: ΔADF= ΔBED (c.g.c)

⇒ DF=ED (hai cạnh tương ứng) (6)

Xét ΔADF và ΔCFE, ta có:

AD = CF (gt)

∠A =∠C =60^o (vì tam giác ABC đều)

AF = CE (chứng minh trên)

suy ra: ΔADF= ΔCFE (c.g.c)

Nên: DF = FE (hai cạnh tương ứng) (7)

Từ (6) và (7) suy ra: DF = ED = FE

Vậy tam giác DFE đều

Bài 78 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC. Gọi giao điểm của đường thẳng này với AB, AC theo thứ tự là D,E.

Chứng minh rằng: DE = BD + CE

Lời giải:

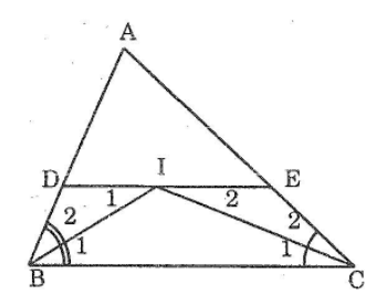
Ta có: DI // BC (giả thiết)

Suy ra:∠I₁ =∠B₁(so le trong) (1)

Lại có:∠B₁ =∠B₂ (2)

(vì BI là tia phân giác góc ABC)

Từ (1) và (2) suy ra:∠I₁ =∠B₂

=>∆BDI cân tại D =>BD=DI (3)

Mà IE // BC (gt) => ∠I₂ =∠C₁ (so le trong) (4)

Đồng thời: ∠C₁=∠C₂ (vì CI là phân giác của góc ACB) (5)

Từ (4) và (5) suy ra: ∠I₂=∠C₂. Suy ra ∠CEI cân tại E

Suy ra: CE = EI (6)

Từ (3) và (6) suy ra: BD + CE = DI + EI = DE

Bài 79 trang 148 sách bài tập Toán 7 Tập 1: Cho đường tròn tâm O đường kính AB. Gọi M là điểm nằm trên đường tròn, tính số đo góc AMB.

Lời giải:

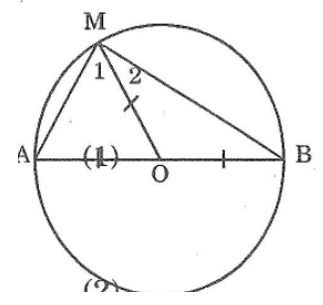
Nối OM, ta có:

OA = OM (bán kính đường tròn tâm O)

Nên ΔOAM cân tại O

⇒∠A =∠M₁(tính chất tam giác cân)(1)

OM = OB (bán kính đường tròn tâm O)

Suy ra: ΔOBM cân tại O

⇒∠B =∠M₂(tính chất tam giác cân) (2)

Trong ΔAMB ta có:

∠A + ∠AMB + ∠B = 180º (tổng ba góc trong tam giác)

⇒∠A +∠B +∠M₁+∠M₂ =180 (3)

Từ (1), (2) và (3) suy ra: 2(∠M₁ + ∠M₂)=180^o

Vậy: ∠M₁+∠M₂=90^o hay ∠(AMB) =90^o

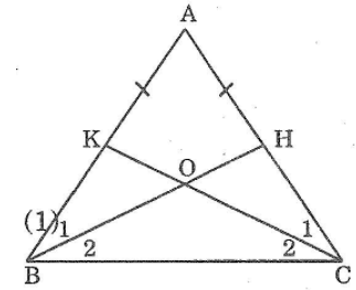
Bài 80 trang 148 sách bài tập Toán 7 Tập 1: Đặt đề toán theo hình dưới đây. Sau đó vẽ lại hình theo đề toán rồi đo goác DAE

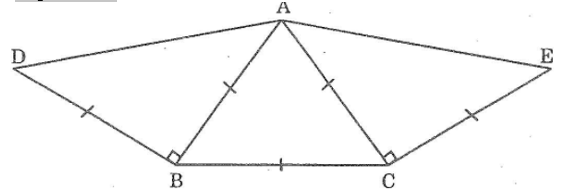
Lời giải:

Đề toán:

Vẽ tam giác ABC đều

Vẽ tam giác ABD vuông cân tại B sao cho D và C nằm trên hai nửa mặt phẳng bờ chứa đường thẳng AB.

Vẽ tam giác ACE vuông cân tại C sao cho E và B nằm trên hai nửa mặt phẳng đối có bờ chứa đường thẳng AC

Đo ∠DAE =150^o

Chứng minh:

Bài 81 trang 148 sách bài tập Toán 7 Tập 1: Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình dưới ) là tam giác nhọn.

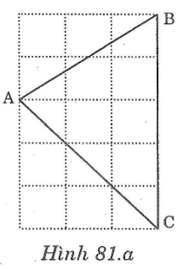
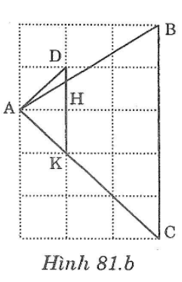
Lời giải:

Nối A với D tạo thành đường chéo ô vuông

Gọi K giao điểm AC với đỉnh ô vuông, H là giao điểm DK với đường kẻ ngang ô vuông đi qua A. ( như hình vẽ)

Ta có: ΔAHK vuông cân tại H =>∠HAK =45^o

ΔAHD vuông cân tại H=>∠HAD =45^o

=>∠DAK =∠HAK +∠HAD =45^o+45^o=90^o

hay ∠DAC =90^o

=>∠BAC < 90^o

Hình vuông có 4 góc, mỗi góc bằng 900. Từ hình vẽ suy ra: ∠ACB < 90^o và ∠ABC <90^o

Vậy tam giác ABC là tam giác nhọn

Bài 6.1 trang 148 sách bài tập Toán 7 Tập 1: Góc ADB trên hình bs 3 có số đo bằng

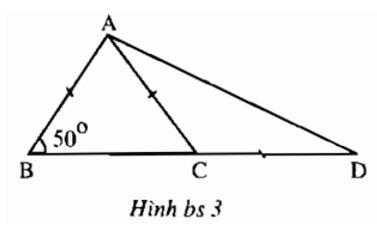
(A) 20^o;

(B) 25^o;

(C) 30^o;

(D) 35^o;

Hãy chọn phương án đúng.

Lời giải:

+) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A

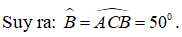
+) Tam giác ACD có góc ACB là góc ngoài của tam giác nên:

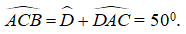
+) Lại có: AC = CD ( giả thiết) nên tam giác ACD cân tại C.

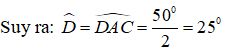
Chọn đáp án B

Bài 6.2 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BC lấy điểm D sao cho BD = BA. Tính số đo góc ADB

Lời giải:

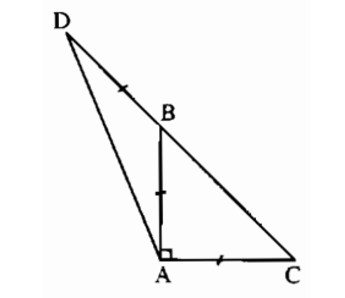
+) Do tam giác ABC vuông cân tại A nên:

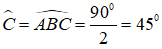
+) Tam giác ABD có AB = BD nên tam giác ABD cân tại B.

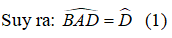
+) Tam giác ABD có góc ABC là góc ngoài tam giác tại đỉnh B nên:

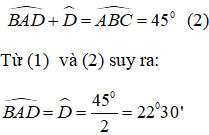
Bài 6.3 trang 148 sách bài tập Toán 7 Tập 1: Cho tam giác cân ABC có ∠A= 100^o. Trên cạnh BC lấy điểm D và E sao cho BD = BA, CE = CA. Tính số đo góc DAE.

Lời giải:

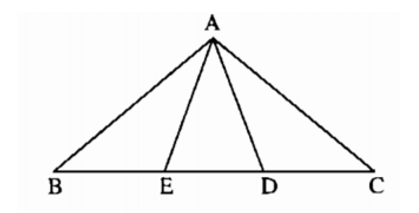
+) Ta có:

(tổng ba góc trong 1 tam giác)

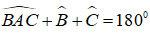
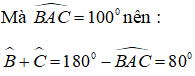
Lại có: tam giác ABC là tam giác cân tại A nên:

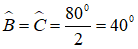
+)Xét tam giác ABD có BA= BD (giả thiết) nên tam giác ABD cân tại B.

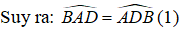
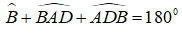
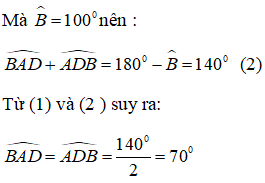
Lại có; ( tổng ba góc trong 1 tam giác)

+) Tương tự, ta có tam giác AEC cân tại C ( vì CA =CE)

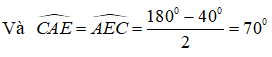
+) Xét tam giác ADE có:

( tổng ba góc trong tam giác)

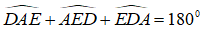
Suy ra:

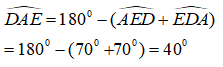
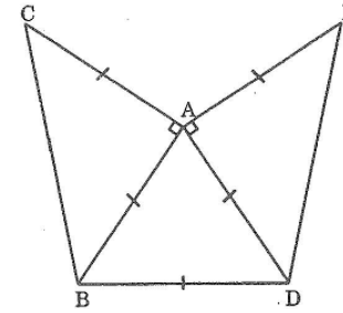
Bài 6.4 trang 148 sách bài tập Toán 7 Tập 1: Cho hình bs 4. Chứng minh rằng :

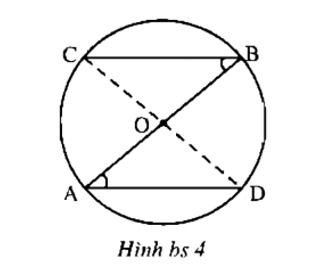
a) C,O,D thẳng hàng ;

b) BC = AD

Lời giải:

+) Xét tam giác OAD có: OA = OD (= bán kính đường tròn)

Suy ra tam giác OAD cân tại O.

Suy ra: ∠A = ∠D ( tính chất tam giác cân). (1)

+) Xét tam giác OBC có: OB = OC (= bán kính đường tròn)

Suy ra tam giác OBC cân tại O.

Suy ra: ∠B = ∠C ( tính chất tam giác cân). (2)

+) Lại có: ∠A = ∠B ( giả thiết) (3)

Từ (1); (2) và (3) suy ra: ∠A = ∠B = ∠C = ∠D

Vậy hai tam giác cân OAD và OBC có góc ở đáy bằng nhau nên góc ở đỉnh bằng nhau: ∠AOD = ∠BOC (4).

+) Ta có: ∠AOD + ∠DOB = 180º ( hai góc kề bù) (5)

Từ (4) và (5) suy ra: ∠BOC + ∠DOB = 180º hay 3 điểm C, O và D thẳng hàng.

b) Xét tam giác OAD và ∆ OCB có:

OA = OC ( = bán kính đường tròn)

∠AOD = ∠BOC ( hai góc đối đỉnh)

OD = OB ( = bán kính đường tròn)

Suy ra:∆ OAD = ∆ OCB ( c.g.c)

Suy ra: AD = BC ( hai cạnh tương ứng).

Xem thêm các bài giải sách bài tập Toán lớp 7 chọn lọc, chi tiết khác:

• Bài 7: Định lí Pi-ta-go
• Bài 8: Các trường hợp bằng nhau của tam giác vuông
• Ôn tập chương 2
• Bài 1: Thu thập số liệu thống kê, tần số
• Bài 2: Bảng "tần số" các giá trị của dấu hiệu

Lời giải bài tập lớp 7 sách mới:

• Giải bài tập Lớp 7 Kết nối tri thức
• Giải bài tập Lớp 7 Chân trời sáng tạo
• Giải bài tập Lớp 7 Cánh diều

---