Sách bài tập Toán 7 Ôn tập chương 2

Sách bài tập Toán 7 Ôn tập chương 2

Bài 103 trang 152 sách bài tập Toán 7 Tập 1: Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. chứng minh rằng CD là đường trung trực của AB.

Lời giải:

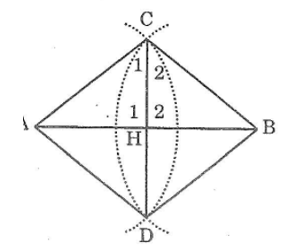
Gọi H là giao điểm của AB và CD

Nối AC, AD,BC,BD

Xét ΔACD và ΔBCD, ta có:

AC = BC

(bán kính hai cung tròn bằng nhau)

AD = BD

CD cạnh chung

Suy ra: ΔACD = ΔBCD(c.c.c)

Suy ra: ∠C₁ = ∠C₂ (hai góc tương ứng)

Xét hai tam giác AHC và BHC. Ta có:

AC = BC (bán kính hai cung tròn bằng nhau)

∠C₁ = ∠C₂ (chứng minh trên)

CH cạnh chung

Suy ra: ΔAHC = ΔBHC(c.g.c)

Suy ra: AH = BH (hai cạnh tương ứng) (1)

Ta có : ∠H₁ = ∠H₂ (hai góc tương ứng)

∠H₁ + ∠H₂ =180° (hai góc kề bù)

Suy ra: ∠H₁ = ∠H₂ = 90^o ⇒ CD ⊥ AB (2)

Từ (1) và (2) suy ra CD là đường trung trực của AB

Bài 104 trang 152 sách bài tập Toán 7 Tập 1: Cho tam giác ADE cân tại A. Trên cạnh DE lấy các điểm B và C sao cho DB = EC < 1/2 DE

a. Tam giác ABC là tam giác gì? Chứng minh điều đó?

b. Kẻ BM ⊥AD, kẻ CN⊥AE. Chứng minh rằng BM = CN

c. Gọi I là giao điểm của MB và NC. Tam giác IBC là tam giác gì? Chứng minh điều đó?

d. Chứng minh rằng AI là tia phân giác của góc BAC

Lời giải:

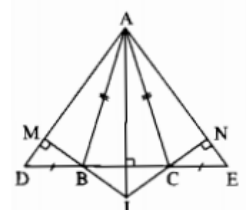
a) Do ΔADE cân tại A nên ∠D =∠E

Xét ΔABD và ΔACE, ta có:

AD = AE (gt)

∠D =∠E (chứng minh trên)

DB=EC (gt)

Suy ra: ΔABD= ΔACE(c.g.c)

Suy ra: AB = AC (hai cạnh tương ứng)

Vậy: ΔABC cân tại A

b) Xét hai tam giác vuông BMD và CNE, ta có:

∠(BMD) = ∠(CNE) =90^o

BD = CE (gt)

∠D =∠E (chứng minh trên)

Suy ra: ΔBMD= ΔCNE(cạnh huyền,góc nhọn)

Do đó,BM = CN ( hai cạnh tương ứng).

c) Ta có: ΔBMD=ΔCNE(chứng minh trên)

Suy ra: ∠DBM =∠ECN (hai góc tương ứng)

Lại có: ∠DBM =∠IBC (đối đỉnh) và ∠ECN =∠ICB (đối đỉnh)

Suy ra: ∠IBC =∠ICB hay ΔIBC cân tại I

d) Xét ΔABI và ΔACI, ta có:

AB = AC (chứng minh trên)

IB = IC ( vì ΔIBC cân tại I)

AI cạnh chung

Suy ra: ΔABI= ΔACI(c.c.c) =>∠BAI =∠CAI ̂(hai góc tương ứng)

Vậy AI là tia phân giác của góc ∠BAC

Bài 105 trang 153 sách bài tập Toán 7 Tập 1: Cho hình dưới trong đó AE ⊥BC. Tính AB biết AE = 4m; AC = 5m; BC = 9m

Lời giải:

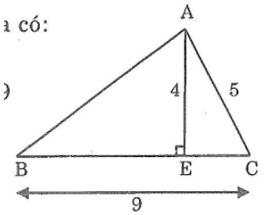
Áp dụng định lý pitago vào tam giác vuông AEC ta có:

AC²=AE²+EC²

=>EC²=AC²-AE²=5²-4²=25-16=9

=>EC=3M

Ta có: BC = BE + EC

BE = BC – EC = 9 – 3 = 6(m)

Áp dụng định lí pitago vào tam giác vuông AEB, ta có:

AB²=AE²+EB²=4²+6²=16+36=52

Suy ra: AB = √52(m) ≈7,2m

Bài 106 trang 153 sách bài tập Toán 7 Tập 1: Tìm các tam giác bằng nhau trong hình bên

Lời giải:

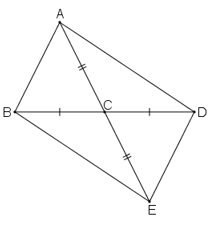
Bài 107 trang 153 sách bài tập Toán 7 Tập 1: Tìm các tam giác cân trên hình dưới

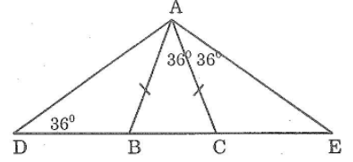
Lời giải:

+) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A.

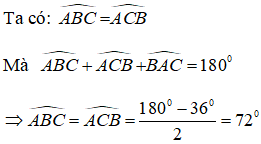
+) Xét tam giác ABD có góc ABC là góc ngoài tam giác tại đỉnh B nên:

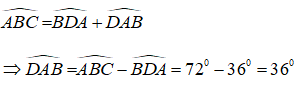
Do tam giác ABD có: 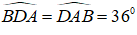nên tam giác ABD cân tại B.

+) Ta có:

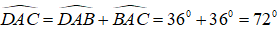
Tam giác ADC có: 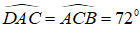nên tam giác ADC cân tại D.

+) Xét tam giác ACE có góc ACB là góc ngoài tam giác tại đỉnh C nên:

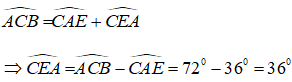
Do tam giác ACE có: 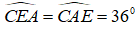nên tam giác ACE cân tại C.

+) Ta có:

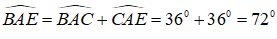
Tam giác ABE có: 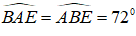nên tam giác ABE cân tại E.

+) Tam giác ADE có: 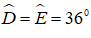nên tam giác này cân tại A.

Vậy có tất cả 6 tam giác đều là: ABD, ABC, ACE, AEB; ADC và ADE.

Bài 108 trang 153 sách bài tập Toán 7 Tập 1: Bạn Mai vẽ tia phân giác của một góc như sau: đánh dấu trên hai cạnh của bốn góc bốn đoạn thẳng bằng nhau: OA = AB = OC = CD (hình dưới). Kẻ các đoạn AD, BC chúng cắt nhau ở K. Hãy giải thích vì sao OK là tia phân giác của góc O.

Hướng dẫn: chứng minh rằng:

a. ΔOAD=ΔOCB

b. ΔKAB=ΔKCD

Lời giải:

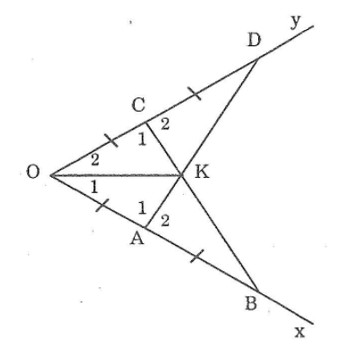
+) Ta có: OC = OA; CD = AB nên:

OC + CD = OA + AB hay OD = OB.

+) Xét ΔOAD và ΔOCB. Ta có:

OA = OC (gt)

∠O chung

OD = OB (chứng minh trên )

Suy ra: ΔOAD= ΔOCB (c.g.c)

Suy ra: ∠D = ∠B(hai góc tương ứng)

Và ∠C₁ =∠A₁ (hai góc tương ứng)

Lại có: ∠C₁+∠C₂ =180°(hai góc kề bù)

Và ∠A₁+∠A₂=180°(hai góc kề bù)

Suy ra: ∠C₂ =∠A₂

Xét ΔKCD và ΔKAB, ta có:

∠B = ∠D (chứng minh trên )

CD=AB (gt)

∠C₂ =∠A₂ (chứng minh trên)

suy ra: ΔKCD= ΔKAB,(g.c.g)

=>KC=KA (hai cạnh tương ứng)

Xét ΔOCK và ΔOAK, ta có:

OC = OA (gt)

OK chung

KC = KA (chứng minh trên)

Suy ra: ΔOCK = ΔOAK (c.c.c)

=> ∠O₁=∠O₂̂(hai góc tương ứng)

Vậy OK là tia phân giác góc O

Bài 109 trang 153 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A, kẻ BH ⊥ AC. Gọi D là một điểm thuộc cạnh đáy BC. Kẻ DE ⊥ AC, DF ⊥ AB.

Chứng minh rằng DE + DF = BH

Lời giải:

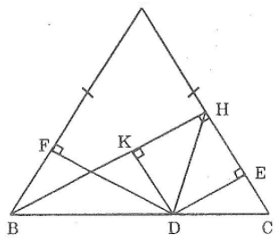
Kẻ DK ⊥ BH

Ta có: BH ⊥AC(gt)

Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)

⇒ ∠KDB = ∠C (hai góc đồng vị)

VìΔABC cân tại A nên ∠B = ∠C (tính chất tam giác cân)

Suy ra: ∠KDB = ∠B

Xét hai tam giác vuông BFD và DKB, ta có:

∠BFD = ∠DKB = 90^o

BD cạnh huyền chung

∠FBD = ∠KDB (chứng minh trên)

Suy ra:ΔBFD=ΔDKB (cạnh huyền góc nhọn)

⇒ DF = BK (hai cạnh tương ứng)(1)

Nối DH. Xét ΔDEH và ΔHKD, ta có:

∠DEH = ∠DKH = 90^o

DH cạnh huyền chung

∠EHD = ∠KDH (hai góc so le trong)

Suy ra:ΔDEH = ΔDKH( cạnh huyền , góc nhọn)

Suy ra: DE = HK ( hai cạnh tương ứng) (2)

Mặt khác: BH = BK + KH (3)

Từ (1), (2) và (3) suy ra: DF + DE = BH

Bài 110 trang 153 sách bài tập Toán 7 Tập 1: Cho tam giác ABC vuông tại A có AB/AC = 3/4 và BC = 15cm. Tính độ dài AB, AC

Lời giải:

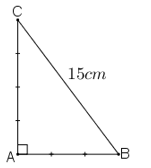
Theo đề bài ta có:

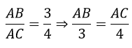
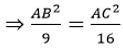
Theo tính chất dãy tỉ số bằng mhau ta có:

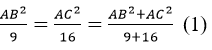
tam giác ABC vuông tại A

Áp dụng định lí pitago vào tam giác ABC ta có:

BC² = AB² + AC² (2)

Từ (1) và (2) suy ra:

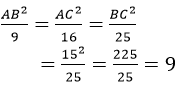
AB² = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)

AC² = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)

Bài II.1 trang 154 sách bài tập Toán 7 Tập 1: Trên hình bs 6 , có bao nhiêu cặp tam giác bằng nhau ?

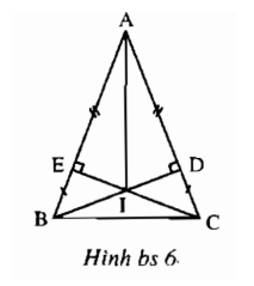
(A) 2;        (B) 3;       (C) 4       (D) 5;

Hãy chọn đáp án đúng

Lời giải:

Chọn D. Năm cặp tam giác bằng nhau là:

ΔAEI = ΔADI, ΔBEI = ΔCDI, ΔAIB = ΔAIC, ΔBEC = ΔCDE, ΔABD = ΔACE.

Bài II.2 trang 154 sách bài tập Toán 7 Tập 1: Cho hình bs 7. Chứng minh rằng OA = OB

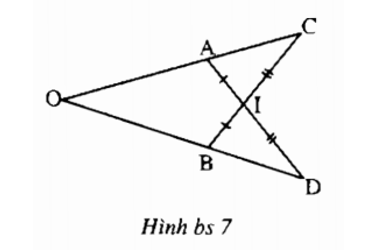
Lời giải:

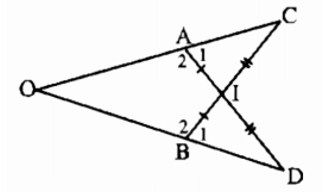
+) Xét ∆AIC và ∆BID có:

AI = BI (giả thiết)

∠AIC = ∠BID ( hai góc đối đỉnh).

IC = ID ( giả thiết)

Suy ra: ∆AIC = ∆BID (c.g.c)

Suy ra: ∠C = ∠D; ∠A₁ = ∠B₁ (1)

+) Lại có: ∠A₁ + ∠A₂ = 180º (hai góc kề bù)

Và ∠B₁ + ∠B₂ = 180º (hai góc kề bù)

Suy ra: ∠A₂ = ∠B₂

+) Xét tam giác OAD và ∆ OBC có:

∠A₂ = ∠B₂ (chứng minh trên)

AD = BC (vì AI + ID = BI + IC)

∠D = ∠C (chứng minh trên)

Suy ra: ∆OAD = ∆ OBC (g.c.g)

Suy ra: OA = OB (hai cạnh tương ứng).

Bài II.3 trang 154 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Trên Tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD

a) Chứng minh rằng IB = IC, ID = IE.

b) Chứng minh rằng BC song song DE.

c) Gọi M là trung điểm BC. Chứng minh rằng ba điểm A, M, I thẳng hàng.

Lời giải:

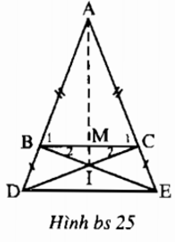
a) +)Theo giả thiết ta có: AB = AC và BD = CE nên:

AB + BD = AC + CE hay AD = AE.

+) Xét ΔABE và ΔACD có:

AB = AC (gt)

∠A chung

AE = AD (chứng minh trên)

⇒ ΔABE = ΔACD (c.g.c)

⇒ BE = CD (2 cạnh tương ứng) (1)

và ∠ABE = ∠ACD (2 góc tương ứng) (2)

Tam giác ABC cân nên ∠B1 = ∠C1. (3)

Từ (2) và (3) ⇒ ∠ABE - ∠B1 = ∠ACD - ∠C1, tức là ∠B2 = ∠C2.

⇒ ΔBIC cân tại I ⇒ IB = IC. (4)

Từ (1) và (4) suy ra BE - IB = CD – IC, tức là IE = ID.

b) Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.

c) Xét ΔABM và ΔACM có:

AB = AC ( giả thiết)

BM = CM ( vì M là trung điểm BC )

AM chung

⇒ ΔABM = ΔACM (c.c.c)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180^o

⇒ ∠AMB = ∠AMC = 90^o hay AM ⊥ BC

Chứng minh tương tự ta có: IM ⊥ BC

⇒ A, I, M thẳng hàng (Qua 1 điểm ta kẻ được duy nhất 1 đường thẳng vuông góc với đường thẳng cho trước)

Xem thêm các bài giải sách bài tập Toán lớp 7 chọn lọc, chi tiết khác:

• Bài 1: Thu thập số liệu thống kê, tần số
• Bài 2: Bảng "tần số" các giá trị của dấu hiệu
• Bài 3: Biểu đồ
• Bài 4: Số trung bình cộng
• Ôn tập chương 3 - Phần Đại số

Lời giải bài tập lớp 7 sách mới:

• Giải bài tập Lớp 7 Kết nối tri thức
• Giải bài tập Lớp 7 Chân trời sáng tạo
• Giải bài tập Lớp 7 Cánh diều

---