Sách bài tập Toán 7 Bài 8: Các trường hợp bằng nhau của tam giác vuông

Sách bài tập Toán 7 Bài 8: Các trường hợp bằng nhau của tam giác vuông

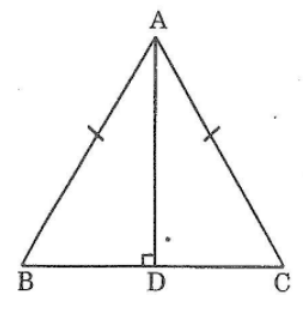
Bài 93 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác cân tại A. Kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A

Lời giải:

Xét hai tam giác vuông ADB và ADC, ta có:

∠(ADB) =∠(ADC) = 90^o

AB = AC (giả thiết)

AD cạnh chung

Suy ra: ΔADB= ΔADC(cạnh huyền, cạnh góc vuông)

⇒ ∠(BAD) =∠(CAD) (hai góc tương ứng)

Vậy AD là tia phân giác ∠(BAC)

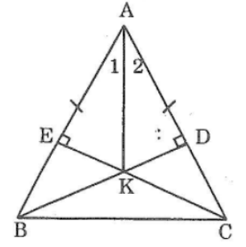
Bài 94 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE. Chứng minh rằng AK là tia phân giác của góc A.

Lời giải:

Xét ΔADB vuông tại D và ΔAEC vuông tại E, ta có:

AB = AC (giả thiết)

∠(BAC) chung

⇒ ΔADB = ΔAEC (cạnh huyền, góc nhọn)

⇒ AD = AE (hai cạnh tương ứng)

Xét ΔADK vuông tại D và ΔAEK vuông tại E có:

AD = AE (chứng minh trên)

AK cạnh chung

⇒ ΔADK = ΔAEK (cạnh huyền, cạnh góc vuông)

⇒ ∠(DAK) = ∠(EAK) (hai góc tương ứng)

Vậy AK là tia phân giác của góc BAC.

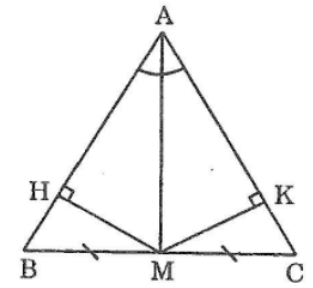
Bài 95 trang 151 sách bài tập Toán 7 Tập 1: Tam giác ABC có M là trung điểm BC,AM là tia phân giác góc A. Kẻ MH vuông góc với AB, MK vuông góc với AC. Chứng minh rằng:

a. MH = MK

b. ∠B =∠C

Lời giải:

Xét hai tam giác vuông AHM và AKM, ta có:

∠(AHM) =∠(AKM) =90^o

Cạnh huyền AM chung

∠(HAM) =∠(KAM) (gt)

⇒ ΔAHM= ΔAKM (cạnh huyền, góc nhọn)

Suy ra: MH = MK (hai cạnh tương ứng)

Xét hai tam giác vuông MHB và MKC, ta có:

∠(MHB) =∠(MKC) =90^o

MH = MK (chứng minh trên)

MC = MB (gt)

⇒ ΔMHB= ΔMKC (cạnh huyền- cạnh góc vuông)

Suy ra ∠B =∠C (hai góc tương ứng)

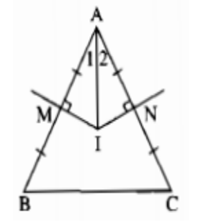
Bài 96 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Các đường trung trực của AB, AC cắt nhau ở I. chứng minh rằng AI là tia phân giác góc A.

Lời giải:

Gọi M, N là trung điểm của AB và AC.

Ta có: AM = 1/2 AB (gt); AN = 1/2 AC (gt)

Mà AB = AC (gt)

⇒ AM = AN

Xét hai tam giác vuông AMI và ANI, ta có:

∠(AMI) = ∠(ANI) = 90^o

AM = AN (chứng minh trên)

AI cạnh huyền chung

⇒ ΔAMI= ΔANI (cạnh huyền, cạnh góc vuông)

⇒ ∠(A₁) = ∠(A₂) (hai góc tương ứng)

Vậy AI là tia phân giác của ∠(BAC)

Bài 97 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc với AB, qua C kẻ đường thẳng vuông góc với AC, chúng cắt nhau tại D. Chứng minh rằng AD là tia phân giác của góc A.

Lời giải:

Xét hai tam giác vuông ABD và ACD, ta có:

∠(ABD) =∠(ACD) =90^o

Cạnh huyền AD chung

AB = AC (giả thiết)

⇒ ΔABD= ΔACD (cạnh huyền, cạnh góc vuông)

Suy ra: ∠(A₁ ) =∠(A₂) (hai góc tương ứng)

Suy ra AD là tia phân giác góc A

Bài 98 trang 151 sách bài tập Toán 7 Tập 1: Tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Chứng minh rằng tam giác ABC là tam giác cân.

Lời giải:

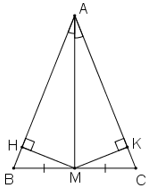
Kẻ MH ⊥ AB, MK ⊥ AC

Xét hai tam giác vuông AHM và AKM, ta có:

∠(AHM) =∠(AKM) = 90^o

Cạnh huyền AM chung

∠(HAM) = ∠KAM) (gt)

⇒ ΔAHM = ΔAKM (cạnh huyền, góc nhọn)

Suy ra: MH = MK (hai cạnh tương ứng)

Xét hai tam giác vuông MHB và MKC, ta có:

∠(MHB) = ∠(MKC) = 90^o

MB = MC ( vì M là trung điểm BC).

MH = MK (chứng minh trên)

⇒ ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)

Suy ra: ∠B = ∠C (hai góc tương ứng)

Vậy tam giác ABC cân tại A.

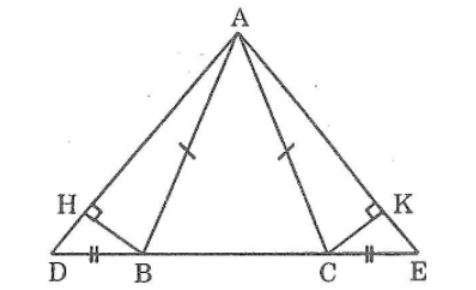
Bài 99 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối của tai BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông với AD, kẻ CK vuông góc với AE. Chứng minh rằng:

a) BH = CK

b) ΔABH= ΔACK

Lời giải:

a) Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)

Ta có: ∠(ABC) +∠(ABD) =180^o(hai góc kề bù)

∠(ACB) +∠(ACE) =180^o(hai góc kề bù)

Suy ra: ∠(ABD) =∠(ACE)

Xét ΔABD và ΔACE, ta có:

AB = AC (gt)

∠(ABD) =∠(ACE) (chứng minh trên)

BD=CE (gt)

Suy ra: ΔABD= ΔACE (c.g.c)

⇒∠D =∠E (hai góc tương ứng)

Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:

∠(BHD) =∠(CKE) = 90º

BD=CE (gt)

∠D =∠E (chứng minh trên)

Suy ra: ΔBHD= ΔCKE (cạnh huyền – góc nhọn)

Suy ra: BH = CK (hai cạnh tương ứng)

b) Xét ΔABH và ΔACK, ta có:

AB = AC (gt)

∠(AHB) =∠(AKC) =90^o

BH=CK ( chứng minh trên)

Suy ra: ΔABH= ΔACK (cạnh huyền– cạnh góc vuông)

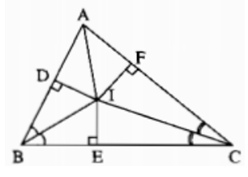
Bài 100 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác ABC. Các tia phân giác của các góc B và C cát nhau tại I. chứng minh rằng AI là tia phân giác của góc A.

Hướng dẫn: từ I, kẻ các đường vuông góc với các cạnh của tam giác ABC.

Lời giải:

Kẻ: ID⊥AB, IE⊥BC, IF⊥AC

Xét hai tam giác vuông ΔIBD và ΔIEB, ta có:

∠(DBI) =∠(EBI) (gt)

∠(IDB) =∠(IEB) =90^o

BI cạnh chung

Suy ra: ΔIDB= ΔIEB(cạnh huyền, góc nhọn)

Suy ra: ID = IE ( hai cạnh tương ứng)

Xét hai tam giác vuông ΔIEC và ΔIFC, ta có:

∠(ECI) =∠(FCI)

∠(IEC) =∠(IFC) =90^o

CI cạnh huyền chung

Suy ra: ΔIEC= ΔIFC(cạnh huyền góc nhọn)

Suy ra: IE = IF (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra: ID = IF

Xét hai tam giác vuông ΔIDA và ΔIFA, ta có:

ID=IF

∠(IDA) =∠(IFA) =90^o

AI cạnh huyền chung

Suy ra: ΔIDA= ΔIFA(cạnh huyền.cạnh góc vuông)

Suy ra: ∠(DAI) =∠(FAI) (hai góc tương ứng)

Vậy AI là tia phân giác góc A

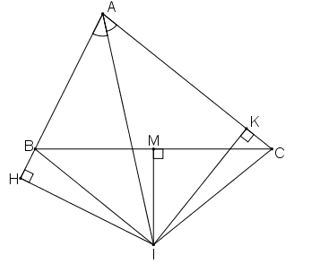
Bài 101 trang 151 sách bài tập Toán 7 Tập 1: Cho tam giác AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. kẻ IH vuông góc với đường thẳng AB, kẻ IK vuông góc với đường thẳng AC. Chứng minh rằng BH = CK.

Lời giải:

Gọi đường trung trực của BC cắt BC tại M.

Xét ΔBMI và ΔCMI, ta có:

∠(BMI) = ∠(CMI) = 90^o (gt)

BM = CM ( vì M là trung điểm của BC )

MI cạnh chung

Suy ra: ΔBMI = ΔCMI(c.g.c)

Suy ra: IB = IC ( hai cạnh tương ứng)

Xét hai tam giác vuông ΔIHA và ΔIKA, ta có:

∠(HAI) = ∠(KAI) ( vì AI là tia phân giác của góc BAC).

∠(IHA) = ∠(IKA) = 90^o

AI cạnh huyền chung

Suy ra: ΔIHA = ΔIKA(cạnh huyền góc nhọn)

Suy ra: IH = IK (hai cạnh tương ứng)

Xét hai tam giác vuông ΔIHB và ΔIKC, ta có:

IB = IC ( chứng minh trên )

∠(IHB) =∠(IKC) =90^o

IH = IK (chứng minh trên)

Suy ra: ΔIHB = ΔIKC(cạnh huyền.cạnh góc vuông)

Suy ra: BH = CK(hai cạnh tương ứng)

Bài 8.1 trang 152 sách bài tập Toán 7 Tập 1: Trong các khẳng định sau, khẳng định nào là đúng, khẳng định nào là sai ?

Các tam giác vuông ABC và DEF có ∠A=∠D=90^o, AC=DE bằng nhau nếu có thêm :

a) BC = EF;

b) ∠C = ∠E;

c) ∠C = ∠F;

Lời giải:

Xét hai tam giác vuông ABC và DFE có: ∠A = ∠D = 90º ; AC=DE

a) Thêm điều kiện BC=EF thì ΔABC=ΔDFE (cạnh huyền - cạnh góc vuông).

b) Thêm điều kiện ∠C = ∠E thì ΔABC=ΔDFE (g.c.g).

c) Thêm điều kiện ∠C = ∠F thì ta không thể kết luận ΔABC=ΔDFE

a) Đúng;

b) Đúng;

c) Sai.

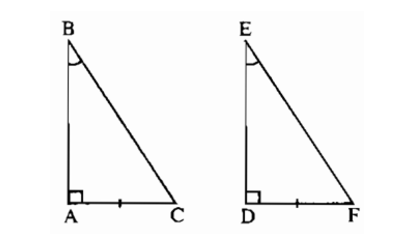
Bài 8.2 trang 152 sách bài tập Toán 7 Tập 1: Các tam giác vuông ABC và DEF có ∠A = ∠D = 90^o,AC = DF,∠B = ∠E.Các tam giác vuông có bằng nhau không

Lời giải:

Bài 8.3 trang 152 sách bài tập Toán 7 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, Trên tia đối của tia CB lấy điểm E sao cho ∠BAD = ∠CAE. Kẻ BH vuông góc với AD (H ∈ AD). kẻ CK vuông góc với AE (K ∈ AE). Chứng minh rằng :

a) BD = CE

b) BH = CK

Lời giải:

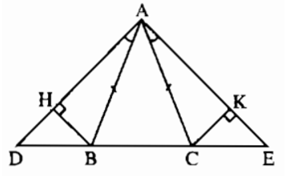
a) +) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)

Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)

∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)

Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE

+) Xét ΔABD và ΔACE có:

∠DAB = ∠EAC ( giả thiết)

AB = AC (vì tam giác ABC cân tại A)

∠ABD = ∠ACE ( chứng minh trên )

⇒ ΔABD = ΔACE (g.c.g)

⇒ BD = CE ( hai cạnh tương ứng)..

b) Xét tam giác BHA và ∆CKA có

∠AHB = ∠AKC = 90º

AB = AC ( vì tam giác ABC cân tại A).

∠HAB = ∠KAC ( giả thiết)

Suy ra ΔBHA = ΔCKA (cạnh huyền – góc nhọn), suy ra BH = CK.

Xem thêm các bài giải sách bài tập Toán lớp 7 chọn lọc, chi tiết khác:

• Ôn tập chương 2
• Bài 1: Thu thập số liệu thống kê, tần số
• Bài 2: Bảng "tần số" các giá trị của dấu hiệu
• Bài 3: Biểu đồ
• Bài 4: Số trung bình cộng

Lời giải bài tập lớp 7 sách mới:

• Giải bài tập Lớp 7 Kết nối tri thức
• Giải bài tập Lớp 7 Chân trời sáng tạo
• Giải bài tập Lớp 7 Cánh diều

---