Giáo án Toán 12 Kết nối tri thức Học kì 1 (năm 2024 mới nhất)

Tài liệu Giáo án Toán 12 Kết nối tri thức Học kì 1 mới nhất theo mẫu Kế hoạch bài dạy (KHBD) chuẩn của Bộ GD&ĐT giúp Thầy/Cô dễ dàng soạn giáo án môn Toán 12 theo chương trình sách mới.

Giáo án Toán 12 Kết nối tri thức Học kì 1 (năm 2024 mới nhất)

Xem thử

Chỉ từ 500k mua trọn bộ Kế hoạch bài dạy (KHBD) hay Giáo án Toán 12 Kết nối tri thức bản word chuẩn kiến thức, trình bày đẹp mắt, dễ dàng chỉnh sửa:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Xem thử

Giáo án Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

I. MỤC TIÊU

1. Kiến thức

Học xong bài này, HS đạt các yêu cầu sau:

- Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm này với đạo hàm.

- Nắm được quy tắc xét tính đơn điệu của hàm số.

- Biết vận dụng quy tắc để xét tính đơn điệu của một hàm số.

- Biết vận dụng tính đơn điệu của hàm số vào giải quyết các bài toán thực tế.

- Hiểu được khái niệm cực đại, cực tiểu. Phân biệt được điểm cực trị của hàm số và của đồ thị hàm số; giá trị và điểm cực trị.

- Nắm được điều kiện đủ để hàm số có cực trị.

- Nắm vững quy tắc tìm cực trị của hàm số. Bước đầu vận dụng vào giải các bài toán tìm cực trị đơn giản.

- Hiểu được đồ thị và bảng biến thiên, từ đó chỉ ra được các điểm cực trị, giá trị cực trị.

2. Năng lực

* Năng lực chung:

- Rèn luyện được năng lực mô hình hóa toán học thông qua các bài toán thực tiễn về chuyển động của chất điểm (tình huống mở đầu), số dân của một thị trấn (Bài tập 1.5), doanh số của một sản phẩm mới (Bài tập 1.6) ...; rèn luyện năng lực giải quyết vấn đề toán học thông qua các bài toán về xác định khoảng đồng biến, nghịch biến, tìm điểm cực trị, giá trị cực trị của hàm số.

* Năng lực riêng: tư duy và lập luận toán học; giao tiếp toán học; mô hình hóa toán học; giải quyết vấn đề toán học.

- Tư duy và lập luận toán học: So sánh, phân tích dữ liệu tìm ra mối liên hệ giữa các đối tượng đã cho và nội dung bài học, từ đó có thể áp dụng kiến thức đã học để giải quyết các bài toán.

- Mô hình hóa toán học, giải quyết vấn đề toán học thông qua các bài toán thực tiễn gắn với tính đơn điệu của hàm số.

- Giao tiếp toán học: Trình bày, phát biểu được các khái niệm về tính đơn điệu của hàm số, cực trị của hàm số.

3. Phẩm chất

- Tích cực thực hiện nhiệm vụ khám phá, thực hành, vận dụng.

- Có tinh thần trách nhiệm trong việc thực hiện nhiệm vụ được giao.

- Khách quan, công bằng, đánh giá chính xác bài làm của nhóm mình và nhóm bạn.

- Tự tin trong việc tính toán; giải quyết bài tập chính xác.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. GV: SGK, SGV, Tài liệu giảng dạy, giáo án PPT, PBT (ghi đề bài cho các hoạt động trên lớp), các hình ảnh liên quan đến nội dung bài học, ...

2. HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)

a) Mục tiêu: Giúp HS có hứng thú với nội dung bài học thông qua một tình huống liên quan đến dấu của đạo hàm và tính đơn điệu của hàm số.

b) Nội dung: HS đọc bài toán khởi động và thực hiện bài toán dưới sự dẫn dắt của GV (HS chưa cần giải bài toán ngay).

c) Sản phẩm: HS nắm được các thông tin trong bài toán và dự đoán câu trả lời cho câu hỏi mở đầu theo ý kiến cá nhân.

d) Tổ chức thực hiện:

Bước 1: Chuyển giao nhiệm vụ:

- GV chiếu Slide dẫn dắt, đặt vấn đề qua bài toán mở đầu và yêu cầu HS thảo luận và nêu dự đoán (chưa cần HS giải):

Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức s(t) = t³ – 9t² + 15t, t ³ 0. Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm và thực hiện yêu cầu theo dẫn dắt của GV.

Bước 3: Báo cáo, thảo luận: GV gọi đại diện một số thành viên nhóm HS trả lời, HS khác nhận xét, bổ sung.

Bước 4: Kết luận, nhận định: GV ghi nhận câu trả lời của HS, trên cơ sở đó dẫn dắt HS vào tìm hiểu bài học mới: “Bài học ngày hôm nay giúp chúng ta biết được mối liên hệ giữa tính đơn điệu, cực trị của hàm số với dấu của đạo hàm; từ đó ta có thể áp dụng để giải được bài toán trong phần khởi động trên”.

→ Bài 1. Tính đơn điệu và cực trị của hàm số.

B. HÌNH THÀNH KIẾN THỨC MỚI

Hoạt động 1: Nhận biết tính đơn điệu của hàm số

a) Mục tiêu:

- Nhận biết được định nghĩa hàm số đồng biến, nghịch biến và nhận biết được mối liên hệ giữa dấu của đạo hàm và tính đơn điệu của hàm số.

- Biết cách sử dụng đồ thị hàm số để xác định hàm số đồng biến, nghịch biến.

- Nắm được quy tắc xét tính đơn điệu của hàm số.

- Biết vận dụng quy tắc để xét tính đơn điệu của một hàm số.

b) Nội dung:

- HS tìm hiểu nội dung kiến thức về tính đơn điệu của hàm số theo yêu cầu, dẫn dắt của GV, thảo luận trả lời câu hỏi trong SGK.

c) Sản phẩm: HS ghi nhớ và vận dụng kiến thức về tính đơn điệu của hàm số để thực hành làm các bài tập Ví dụ, Luyện tập, Vận dụng.

d) Tổ chức thực hiện:

HĐ CỦA GV VÀ HS

SẢN PHẨM DỰ KIẾN

Bước 1: Chuyển giao nhiệm vụ: - GV cho HS trao đổi theo bàn và thực hiện HĐ1 để nhận biết định nghĩa hàm số đồng biến, hàm số nghịch biến và nắm được liên hệ giữa sự đồng biến, nghịch biến của hàm số và dáng điệu của đồ thị hàm số. + GV chỉ định một số HS đứng tại chỗ trả lời các câu hỏi của HĐ1. + GV nhận xét và chốt đáp án. - GV đặt câu hỏi dẫn dắt ra Kết luận trong khung kiến thức trọng tâm: “Thế nào là hàm số đồng biến, hàm số nghịch biến?”. - GV viết lên bảng và minh họa phần Kết luận trong khung kiến thức trọng tâm cho HS quan sát và hiểu rõ, đồng thời nhắc nhở HS phần Chú ý. - GV hướng dẫn HS thực hiện Ví dụ 1. + GV trình bày mẫu lời giải Ví dụ 1 cho HS hiểu được cách quan sát đồ thị để xác định tính đồng biến, nghịch biến của hàm số.

1. Tính đơn điệu của hàm số a) Khái niệm tính đơn điệu của hàm số Hoạt động 1: 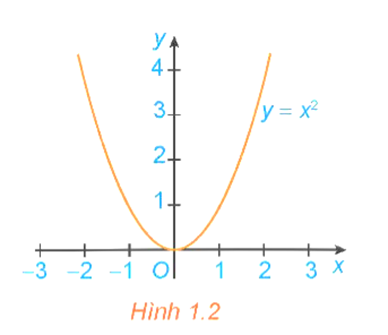a) Hàm số đồng trên khoảng (0; +∞). b) Hàm số nghịch biến trên khoảng (−∞; 0). Kết luận: (SGK – Trang 6) Chú ý: (SGK – Trang 6) Ví dụ 1: (SGK – Trang 6) Lời giải: (SGK – Trang 6)

................................

................................

................................

Giáo án Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

I. MỤC TIÊU

1. Kiến thức

Học xong bài này, HS đạt các yêu cầu sau:

- Biết các khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập hợp số.

- Nắm được quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn.

- Biết cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, một khoảng bằng đạo hàm.

- Phân biệt việc tìm giá trị lớn nhất, giá trị nhỏ nhất với tìm cực trị của hàm số.

- Dựa vào đồ thị chỉ ra được giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

- Biết vận dụng giá trị lớn nhất, giá trị nhỏ nhất vào giải các bài toán thực tế.

2. Năng lực

* Năng lực chung:

- Rèn luyện được năng lực giải quyết vấn đề toán học thông qua các bài toán vận dụng liên quan đến giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

* Năng lực riêng: Tư duy và lập luận toán học, mô hình hóa toán học; giải quyết vấn đề toán học; giao tiếp toán học và sử dụng công cụ, phương tiện học toán.

- Tư duy và lập luận toán học: So sánh, phân tích dữ liệu tìm ra mối liên hệ giữa các đối tượng đã cho và nội dung bài học, từ đó có thể áp dụng kiến thức đã học để giải quyết các bài toán.

- Mô hình hóa toán học, giải quyết vấn đề toán học thông qua các bài toán thực tiễn gắn với giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

- Giao tiếp toán học: Sử dụng ngôn ngữ toán học chính xác, điều này giúp đảm bảo rằng thông điệp được truyền tải một cách chính xác và dễ hiểu cho người đọc.

- Sử dụng công cụ, phương tiện học toán: Sử dụng được máy tính cầm tay để giải phương trình, …

3. Phẩm chất

- Tích cực thực hiện nhiệm vụ khám phá, thực hành, vận dụng.

- Có tinh thần trách nhiệm trong việc thực hiện nhiệm vụ được giao.

- Khách quan, công bằng, đánh giá chính xác bài làm của nhóm mình và nhóm bạn.

- Tự tin trong việc tính toán; giải quyết bài tập chính xác.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. GV: SGK, SGV, Tài liệu giảng dạy, giáo án PPT, PBT (ghi đề bài cho các hoạt động trên lớp), các hình ảnh liên quan đến nội dung bài học,...

2. HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU)

a) Mục tiêu: Giúp HS có hứng thú với nội dung bài học thông qua một tình huống liên quan đến giá trị lớn nhất của hàm số.

b) Nội dung: HS đọc bài toán mở đầu và thực hiện bài toán dưới sự dẫn dắt của GV (HS chưa cần giải bài toán ngay).

c) Sản phẩm: HS nắm được các thông tin trong bài toán và dự đoán câu trả lời cho câu hỏi mở đầu theo ý kiến cá nhân.

d) Tổ chức thực hiện:

Bước 1: Chuyển giao nhiệm vụ:

- GV chiếu Slide dẫn dắt, đặt vấn đề qua bài toán mở đầu và yêu cầu HS thảo luận và nêu dự đoán (chưa cần HS giải):

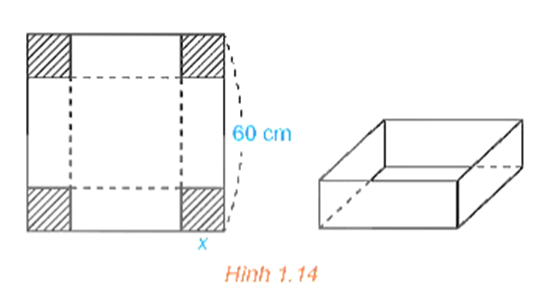
Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (H.1.14). Tính cạnh của các hình vuông bị cắt sao cho thể tích của chiếc hộp là lớn nhất.

Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm và thực hiện yêu cầu theo dẫn dắt của GV.

Bước 3: Báo cáo, thảo luận: GV gọi đại diện một số thành viên nhóm HS trả lời, HS khác nhận xét, bổ sung.

Bước 4: Kết luận, nhận định: GV ghi nhận câu trả lời của HS, trên cơ sở đó dẫn dắt HS vào tìm hiểu bài học mới: “Để giải quyết được bài toán mở đầu và biết được cách xử lý các bài toán tương tự cũng như mở rộng hơn, chúng ta cùng đi tìm hiểu phần nội dung bài học ngày hôm nay”.

→ Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

B. HÌNH THÀNH KIẾN THỨC MỚI

Hoạt động 1: Tìm hiểu định nghĩa giá trị lớn nhất và giá trị nhỏ nhất của hàm số

a) Mục tiêu:

- Biết các khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập hợp số.

- Biết sử dụng các bất đẳng thức cơ bản để tìm giá trị lớn nhất và giá trị nhỏ nhất của một hàm số trên một tập số bằng định nghĩa.

- Biết cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng bằng cách lập bảng biến thiên.

b) Nội dung:

- HS tìm hiểu nội dung kiến thức về giá trị lớn nhất và giá trị nhỏ nhất của hàm số theo yêu cầu, dẫn dắt của GV, thảo luận trả lời câu hỏi trong SGK.

c) Sản phẩm:

- HS ghi nhớ và vận dụng định nghĩa về giá trị lớn nhất và giá trị nhỏ nhất của hàm số để thực hành làm các bài tập ví dụ, luyện tập, vận dụng.

d) Tổ chức thực hiện:

HĐ CỦA GV VÀ HS

SẢN PHẨM DỰ KIẾN

Bước 1: Chuyển giao nhiệm vụ: - GV hướng dẫn cho HS làm HĐ1: Nhận biết khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. + Quan sát đồ thị Hình 1.15 để trả lời các câu hỏi. + HS suy nghĩ làm bài. + GV chỉ định một số HS nêu đáp án. + GV trình bày đáp án lên bảng. - Từ đó, GV tổng quát tiến tới phần khung kiến thức trọng tâm. + HS cần nắm vững các định nghĩa này để hiểu và áp dụng vào bài một cách nhanh chóng và chính xác. - GV nhắc nhở HS phần Chú ý. - GV hướng dẫn HS làm Ví dụ 1 theo hai cách. + GV: Các em cần chú ý đến những bất đẳng thức đặc biệt và nhớ lại cách lập BBT của hàm số ở bài học trước. + GV gọi chỉ định 2 HS đứng tại chỗ cùng mình thực hiện bài tập này, mỗi HS thực hiện 1 cách. + Cả lớp quan sát và ghi bài.

1. Định nghĩa Hoạt động 1: Dựa vào đồ thị ta có: a) Giá trị lớn nhất của hàm số trên đoạn [0; 3] là M = 3 khi x0 = 3. b) Giá trị nhỏ nhất của hàm số trên đoạn [0; 3] là m = −1 khi x0 = 1. Kết luận: Định nghĩa giá trị lớn và giá trị nhỏ nhất của hàm số (SGK – Trang 15). Chú ý: - Khi tìm giá trị lớn nhất (hoặc giá trị nhỏ nhất) của hàm số mà không chỉ rõ tập D thì ta tìm giá trị lớn nhất (hoặc giá trị nhỏ nhất) của hàm số đó trên cả tập xác định của nó. - Để tìm GTLN, GTNN của hàm số trên tập D, ta thường lập BBT và nêu KL. Ví dụ 1: (SGK – Trang 16) Lời giải: (SGK – Trang 16)

................................

................................

................................

Trên đây tóm tắt một số nội dung miễn phí trong bộ Giáo án Toán 12 Kết nối tri thức năm 2024 mới nhất, để mua tài liệu đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

---