Tổng hợp lý thuyết Toán 7 Chương 2 Cánh diều
Với Tổng hợp lý thuyết Toán 7 Chương 2: Số thực sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Tổng hợp lý thuyết Toán 7 Chương 2 Cánh diều
Lý thuyết tổng hợp Toán 7 Chương 2
1. Số vô tỉ
1.1 Khái niệm số vô tỉ
Trong đời sống thực tiễn của con người, ta thường gặp những số không phải là số hữu tỉ. Những số không phải là số hữu tỉ được gọi là số vô tỉ.
Ví dụ: Số Pi (π) là tỉ số giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó và là một số vô tỉ.
1.2 Số thập phân vô hạn không tuần hoàn
Những số thập phân vô hạn mà phần thập phân của nó không có một chu kì nào cả, những số đó được gọi là số thập phân vô hạn không tuần hoàn.
Ví dụ:
Số –1,359130000110578… là số thập phân vô hạn không tuần hoàn.
Số π = 3,14159265358979323846264338… là số thập phân vô hạn không tuần hoàn.
1.3 Biểu diễn thập phân của số vô tỉ
Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.
Ví dụ:
Số –1,359130000110578… là số vô tỉ.
Số π = 3,14159265358979323846264338… là số vô tỉ.
- Nếu a là một số tự nhiên, số nguyên hay số hữu tỉ thì a không thể là số vô tỉ.
2. Căn bậc hai số học
- Căn bậc hai số học của một số a không âm là số x không âm sao cho x2 = a.
- Căn bậc hai số học của số a (a ≥ 0) được kí hiệu là .
- Căn bậc hai số học của số 0 là số 0, viết là: .
Chú ý: Cho a ≥ 0. Khi đó:
+ Đẳng thức = b là đúng nếu b ≥ 0 và b2 = a.
+ .
Ví dụ:
- Ta có 9 > 0 và 92 = 81 nên 9 là căn bậc hai số học của 81. Ta viết: .
- Ta có 0,4 ≥ 0 và (0,4)2 = 0,16 nên 0,4 là căn bậc hai số học của 0,16.
Ta viết .
- Ta có (– 5)2 = 25 nhưng – 5 < 0 nên – 5 không phải căn bậc hai số học của số 25.
Nhận xét:
- Nếu số nguyên dương a không phải là bình phương của bất kì số nguyên dương nào thì là số vô tỉ.
Ví dụ: đều là các số vô tỉ.
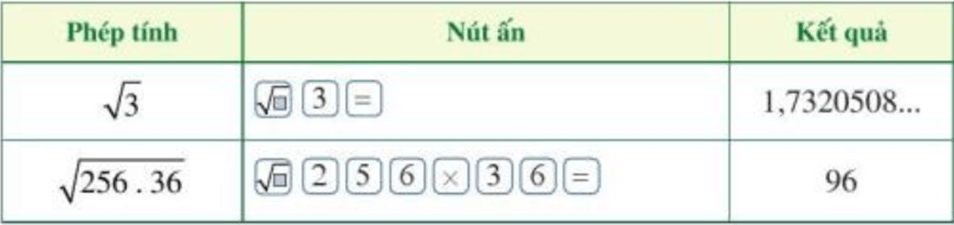
- Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay.
Ví dụ: Để tính và bằng máy tính cầm tay ta làm như sau:
3. Tập hợp số thực
3.1 Số thực
- Số hữu tỉ và số vô tỉ được gọi chung là số thực.
- Tập hợp các số thực được kí hiệu là ℝ.
Ví dụ: Các số 1,2 ; ; ; … là các số thực.
3.2 Biểu diễn thập phân của số thực
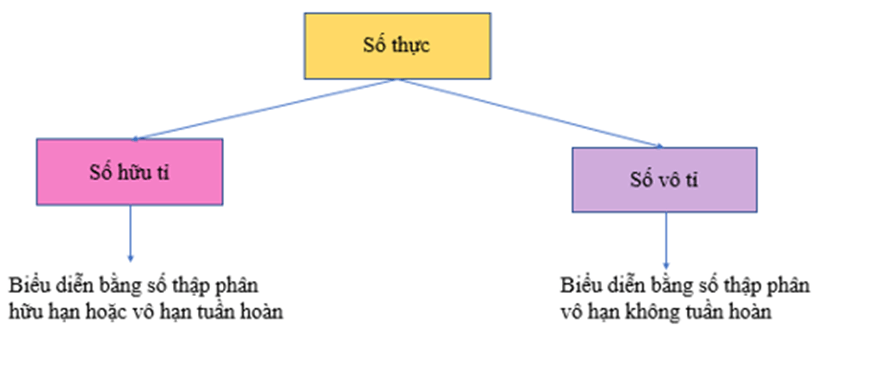
- Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn. Ta có sơ đồ sau:
4. Biểu diễn số thực trên trục số
Tương tự như đối với số hữu tỉ, ta có thể biểu diễn mọi số thực trên trục số, khi đó điểm biểu diễn số thực x được gọi là điểm x.
Ví dụ: Biểu diễn các số thực sau trên trục số:
a) và 2;
b) .
Hướng dẫn giải
a) Số và 2 là hai số hữu tỉ, vì thế để biểu diễn hai số này trên trục số ta thực hiện như cách biểu diễn một số hữu tỉ trên trục số.
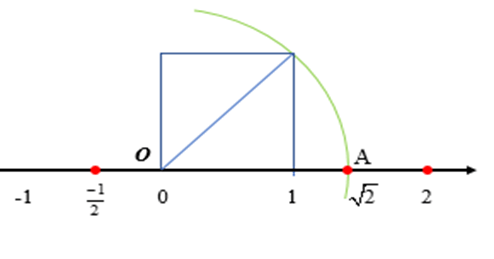
b) Số là một số vô tỉ vì vậy để biểu diễn số trên trục số ta làm như sau:
+ Vẽ một hình vuông với một cạnh là đoạn thẳng có hai đầu mút là điểm gốc 0 và điểm 1. Khi đó, đường chéo của hình vuông có độ dài cạnh bằng .
+ Vẽ một phần đường tròn tâm là điểm gốc 0, bán kính là , cắt trục số tại điểm A nằm bên phải gốc 0. Ta có OA = và A là điểm biểu diễn .
Nhận xét:
- Không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.
- Mỗi số thực được biểu diễn bởi một điểm trên trục số; Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
Vậy trục số còn được gọi là trục số thực.
5. Số đối của một số thực
- Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau.
- Số đối của số thực a kí hiệu là – a.
- Số đối của số 0 là 0.
Nhận xét: Số đối của – a là số a, tức là –(–a) = a.
Ví dụ:
Số đối của số thực là số thực .
6. So sánh các số thực
6.1 So sánh hai số thực
Cũng như số hữu tỉ, trong hai số thực khác nhau luôn có một số nhỏ hơn số kia.
- Nếu số thực a nhỏ hơn số thực b thì ta biết a < b hay b > a.
- Số thực lớn hơn 0 gọi là số thực dương.
- Số thực nhỏ hơn 0 gọi là số thực âm.
- Số 0 không phải là số thực dương cũng không phải số thực âm.
- Nếu a < b và b < c thì a < c.
6.2 Cách so sánh hai số thực
- Ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.
- Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc: Với a, b là hai số thực dương, nếu
a > b thì .
Ví dụ: So sánh các số thực sau:
a) –1,(27) và –1,272 ;
b) và .
Hướng dẫn giải
a) Ta viết –1,(27) = –1,27272727….. sau đó ta so sánh với –1,272.
Hai số –1,27272727… và –1,2720 có phần nguyên và đến hàng phần nghìn giống nhau, cặp chữ số khác nhau đầu tiên bắt đầu từ hàng phần chục nghìn.
Do 7 > 0 nên 1,27272727…..> 1,2720, suy ra –1,27272727…..< –1,2720.
Vậy –1,(27) < –1,272.
b) Ta có: 0 < 7 < 8 nên < .
6.3 Minh họa trên trục số
Giả sử hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số nằm ngang. Ta có nhận xét sau :
- Nếu x < y hay y > x thì điểm x nằm bên trái điểm y;
- Ngược lại nếu điểm x nằm bên trái điểm y thì x < y hay y > x.
Đối với hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số thẳng đứng, ta cũng có nhận xét sau :
- Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y;
- Ngược lại, nếu điểm x nằm phía dưới điểm y thì x < y hay y > x.
Ví dụ:
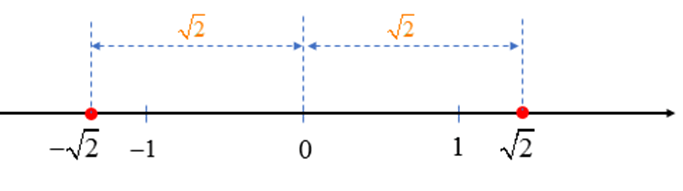
+ Vì < –1 nên trên trục số nằm ngang, điểm nằm bên trái điểm –1.
+ Điểm nằm bên trái điểm , vì vậy < .
7. Khái niệm giá trị tuyệt đối của số thực
- Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu |x|.
Nhận xét:
- Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.
- Hai số thực đối nhau có giá trị tuyệt đối bằng nhau.
Ví dụ:
- Khoảng cách từ điểm 3 đến gốc 0 là 3 nên giá trị tuyệt đối của số 3 là 3, tức là |3| = 3.
- Khoảng cách từ điểm –3 đến gốc 0 là 3 nên giá trị tuyệt đối của số –3 là 3, tức là |–3| = 3.
- Số 3 và –3 là hai số đối nhau, |3| = |–3| = 3.
8. Tính chất giá trị tuyệt đối của số thực
- Nếu x là số dương thì giá trị tuyệt đối của x là chính nó: |x| = x (x > 0).
- Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó: |x| = – x (x < 0).
- Giá trị tuyệt đối của 0 là 0: |0| = 0.
Nhận xét: Với mỗi số thực x, ta có:
+) .
+) |–x| = |x|.
Ví dụ: Tìm |– 76| ; |3,1|
Vì – 76 < 0 nên |–76| = – (–76) = 76
Vì 3,1 > 0 nên |3,1| = 3,1.
Chú ý: Giả sử hai điểm A, B lần lượt biểu diễn hai số thực a, b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|, tức là AB = |a – b|.
Ví dụ: Tính độ dài đoạn thẳng AB trên hình vẽ sau:\
a)
Ta có AB = OA + OB = |–3| + |1| = 3 + 1 = 4.
Hay AB = |–3 – 1| = |–4| = 4.
b)
Ta có AB = OA – OB = |–4| – |–1| = 4 – 1 = 3.
Hay AB = |(–4) – (– 1)| = |– 3| = 3.
9. Làm tròn số
9.1 Số làm tròn
Ở nhiều tình huống thực tiễn ta cần tìm một số thực khác xấp xỉ với số thực đã cho để thuận tiện hơn trong ghi nhớ, đo đạc, hay tính toán. Số thực tìm được như thế được gọi là số làm tròn của số thực đã cho.
Ví dụ:
Hóa đơn tiền điện của gia đình bạn An tháng 9/2021 là 356 870 đồng. Trên thực tế mẹ của An đã trả tiền mặt cho người thu tiền điện 357 000 đồng.
Vậy số 357 000 là số làm tròn của số 356 870.
9.2 Làm tròn số với độ chính xác cho trước
Ta nói số a được làm tròn đến số b với độ chính xác d nếu khoảng cách giữa điểm a và điểm b trên trục số không vượt quá d.
Ví dụ: Làm tròn số 126 đến hàng chục ta được số 130. Khoảng cách giữa hai điểm 126 và 130 trên trục số là 130 – 126 = 4. Khoảng cách này không vượt quá 5. Khi đó ta nói số 126 được làm tròn đến số 130 với độ chính xác 5.
Nhận xét:
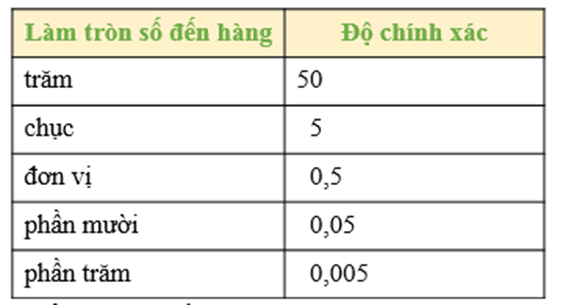
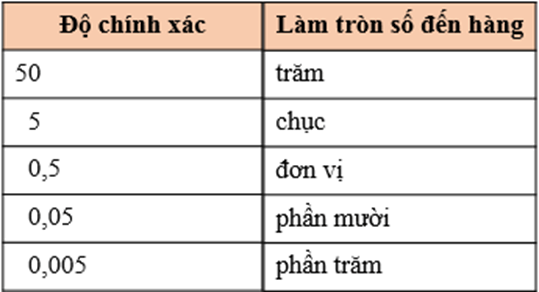
- Khi làm tròn số đến một hàng nào đó thì độ chính xác bằng nửa đơn vị của hàng làm tròn.
- Để làm tròn số với độ chính xác cho trước, ta có thể sử dụng cách ở bảng sau:
- Để làm tròn một số thập phân âm, ta chỉ cần làm tròn số đối của nó rồi đặt dấu “–” trước kết quả.
Ví dụ:
a) Làm tròn số 3,141592653… đến hàng phần trăm.
b) Làm tròn số 128,25 với độ chính xác 0,05.
c) Làm tròn số – 1,9254 với độ chính xác 0,005
d) Làm tròn số với độ chính xác 0,5.
Hướng dẫn giải
a) Ta áp dụng quy tắc làm tròn số thập phân hữu hạn. Do chữ số ở hàng phần nghìn là 1 < 5 nên 3,141592653… ≈ 3,14.
Người ta chứng minh được rằng số 3,141592653… làm tròn đến 3,14 cũng với độ chính xác 0,005.
b) Để làm tròn số 128,25 với độ chính xác 0,05 ta sẽ làm tròn đến hàng phần mười. Áp dụng quy tắc làm tròn số ta được 128,25 ≈ 128,3.
c) Để làm tròn số –1,9254 với độ chính xác 0,005 ta sẽ làm tròn đến hàng phần trăm. Áp dụng quy tắc làm tròn số ta được 1,9254 ≈ 1,93. Vì vậy, – 1,9254 ≈ –1,93.
d)
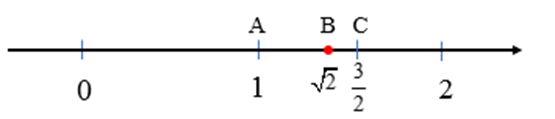
Ta biểu diễn số trên trục số. Khi đó AC = 0,5, điểm B nằm giữa A và C nên AB < AC.
Mà AC = 0,5 nên AB < 0,5, tức là khoảng cách giữa điểm và điểm 1 trên trục số nhỏ hơn 0,5. Vậy với độ chính xác 0,5 thì ≈ 1.
Chú ý: Trong đo đạc và tính toán thực tiễn, ta thường có gắng làm tròn số thực với độ chính xác d nhỏ nhất càng tốt. Trong thực tế, làm tròn số thực là một công việc có nhiều khó khăn. Tuy nhiên, người ta cũng biết một số cách để làm tròn số thực.
10. Ước lượng
Trong thực tiễn, đôi lúc ta không quá quan tâm đến tính chính xác của kết quả tính toán mà chỉ cần ước lượng kết quả, tức là tìm một số gần sát với kết quả chính xác.
Ví dụ: Áp dụng quy tắc làm tròn để ước lượng kết quả của các phéo tính sau:
a) 5,14 + 4,93
b) 60,3 . 49,5
Hướng dẫn giải
a) Làm tròn đến hàng phần mười của mỗi số hạng: 5,14 ≈ 5,1; 4,93 ≈ 4,9
Khi đó 5,14 + 4, 93 ≈ 5,1 + 4,9 = 10
b) Làm tròn đến hàng đơn vị mỗi thừa số ta có: 60,3 ≈ 60; 49,5 ≈ 50.
Khi đó 60,3 . 49,5 ≈ 60 . 50 = 3000.
11. Tỉ lệ thức
Tỉ lệ thức là đẳng thức của hai tỉ số và , viết là .
Chú ý: Tỉ lệ thức còn được viết là a : b = c : d; các số a, b, c, d gọi là các số hạng của tỉ lệ thức.
Ví dụ: Tỉ lệ thức hay còn được viết là 3 : 4 = 6 : 8.
12. Tính chất của tỉ lệ thức
2.1 Tính chất 1
Nếu thì ad = bc.
Ví dụ: Từ tỉ lệ thức suy ra 3.8 = 4.6 = 24.
2.2 Tính chất 2
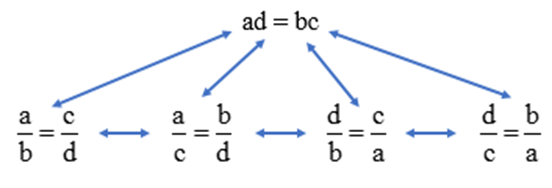
Nếu ad = bc và a, b, c, d đều khác 0 thì ta có các tỉ lệ thức:
; ; ; .
Ví dụ: Từ đẳng thức 2 . 6 = 3 . 4 có thể suy ra bốn tỉ lệ thức sau:
; ; ; .
Nhận xét: Với a, b, c, d đều khác 0 thì từ một trong năm đẳng thức sau đây, ta có thể suy ra các đẳng thức còn lại.
Ví dụ: Từ đẳng thức ta cũng có thể suy ra bốn đẳng thức nữa đó là:
14 . 3 = 6 . 7; ; ; .
13. Khái niệm dãy tỉ số bằng nhau
Những tỉ số bằng nhau và được viết nối với nhau bởi các dấu đẳng thức tạo thành dãy tỉ số bằng nhau.
Chú ý:
- Với dãy tỉ số bằng nhau ta cũng viết a : b = c : d = e : g.
- Khi có dãy tỉ số bằng nhau , ta nói các số a, c, e tỉ lệ với các số b, d, g và viết là a : c : e = b : d : g.
Ví dụ:
- Dãy tỉ số bằng nhau .
- Khi nói ba số x ; y ; z tỉ lệ với các số 2 ; 3 ; 4 thì x : y : z = 2 : 3 : 4 và ta viết được dãy tỉ số bằng nhau: .
14. Tính chất dãy tỉ số bằng nhau
Từ tỉ lệ thức , ta suy ra:
( b ≠ d và b ≠ –d).
Nhận xét: Tính chất trên còn mở rộng cho dãy tỉ số bằng nhau. Chẳng hạn từ dãy tỉ số bằng nhau , ta suy ra:
(giả thiết các tỉ số đều có nghĩa).
Ví dụ: Từ dãy tỉ số , áp dụng tính chất của dãy tỉ số bằng nhau ta có:
.
15. Ứng dụng của dãy tỉ số bằng nhau
Các tính chất của dãy tỉ số bằng nhau có nhiều ứng dụng trong thực tiễn, chẳng hạn, ứng dụng vào bài toán chia đại lượng cho trước thành các phần theo tỉ lệ cho trước.
Ví dụ: Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2 ; 4 ; 5. Tính số viên bi của mỗi bạn, biết rằng ba bạn có tất cả 44 viên bi.
Hướng dẫn giải
Gọi số viên bi của ba bạn Minh, Hùng, Dũng lần lượt là x (viên bi); y (viên bi); z (viên bi).
Ta có: và x + y + z = 44.
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Suy ra x = 2.4 = 8 ; y = 4.4 = 16 ; z = 5.4 = 20.
Vậy Minh có 8 viên bi, Hùng có 16 viên bi, Dũng có 20 viên bi.
16. Đại lượng tỉ lệ thuận
- Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx (với k là một hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.
- Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x tỉ lệ thuận với y theo hệ số tỉ lệ . Ta nói x và y là hai đại lượng tỉ lệ thuận với nhau.
Ví dụ:
a) Nếu y = 2x thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ 2. Khi đó x cũng tỉ lệ thuận với y theo hệ số tỉ lệ .
b) Chu vi đường tròn C và đường kính d liên hệ với nhau bởi công thức C = π . d. Khi đó C tỉ lệ thuận với d theo hệ số tỉ lệ là π (π ≈ 3,14).
17. Tính chất của đại lượng tỉ lệ thuận
Nếu hai đại lượng tỉ lệ thuận với nhau thì :
- Tỉ số hai giá trị tương ứng của chúng luôn không đổi ;
- Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia.
Cụ thể : Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ k. Với mỗi giá trị x1, x2, x3,… khác 0 của x, ta có một giá trị tương ứng y1, y2, y3, … của y. Khi đó :
Ví dụ: Khối lượng và thể tích của các thanh kim loại đồng chất là hai đại lượng tỉ lệ thuận với nhau. Biết hai thanh kim loại đồng chất có thể tích lần lượt là 10 cm3 và 15 cm3. Tính tỉ số khối lượng của hai thanh kim loại đó.
Hướng dẫn giải
Gọi m1 (gam) và m2 (gam) lần lượt là khối lượng của hai thanh kim loại có thể tích 10 cm3 và 15 cm3.
Áp dụng tính chất của đại lượng tỉ lệ thuận ta có .
18. Một số bài toán về đại lượng tỉ lệ thuận
Bài toán 1: Một máy in trong 5 phút in được 120 trang. Hỏi trong 3 phút máy in đó in được bao nhiêu trang?
Hướng dẫn giải
Gọi x (phút), y (trang) lần lượt là thời gian in và số trang mà máy in đã in được. Khi đó mỗi quan hệ giữa thời gian (x) và số trang in được (y) được cho bởi bảng sau:
Thời gian (x) |
x1 = 5 |
x2 = 3 |
Số trang in (y) |
y1 = 120 |
y2 = ? |
Ta có thời gian in tỉ lệ thuận với số trang in được theo hệ số tỉ lệ .
Suy ra . Vì thế y2 = 24 . 3 = 72.
Vậy trong 3 phút máy in in được 72 trang.
Bài toán 2: Hai thanh chì có thể tích là 12 cm3 và 17 cm3. Hỏi mỗi thanh nặng bao nhiêu gam, biết rằng thanh thứ hai nặng hơn thanh thứ nhất 56,5 g?
Hướng dẫn giải
Gọi khối lượng của hai thanh chì tương ứng là m1 gam và m2 gam. Khi đó m2 – m1 = 56,5 (g)
Do khối lượng và thể tích của vật thể là hai đại lượng tỉ lệ thuận với nhau. Do đó, ta có:
.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: .
Suy ra m1 = 12 . 11,3 = 135,6 ; m2 = 17 . 11,3 = 192,1.
Vậy hai thanh chì có khối lượng là 135,6 gam và 192,1 gam.
19. Đại lượng tỉ lệ nghịch
- Nếu đại lượng y liên hệ với đại lượng x theo công thức hay xy = a (với a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
- Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ a. Ta nói x và y là hai đại lượng tỉ lệ nghịch với nhau.
Ví dụ : Nếu thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ –5. Khi đó x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ –5.
20. Tính chất của đại lượng tỉ lệ nghịch
Nếu hai đại lượng tỉ lệ nghịch với nhau thì:
- Tích hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ).
- Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ lệ hai giá trị tương ứng của đại lượng kia.
Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a. Với mỗi giá trị x1, x2, x3, … khác 0 của x, ta có một giá trị tương ứng y1, y2, y3,… của y. Khi đó :
x1 y1 = x2 y2 = x3 y3 = …= a hay
21. Một số bài toán về đại lượng tỉ lệ nghịch
Chú ý :
- Năng suất lao động và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
- Số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Bài toán 1: Cho biết 35 công nhân xây một ngôi nhà hết 168 ngày. Hỏi nếu chỉ có 28 công nhân xây ngôi nhà đó thì hết bao nhiêu ngày (giả sử năng suất làm việc của mỗi công nhân là như nhau).
Hướng dẫn giải
Gọi x (công nhân), y (ngày) lần lượt là số công nhân và thời gian xây xong ngôi nhà. Khi đó, mối quan hệ giữa số công nhân (x) và thời gian xây xong ngôi nhà (y) được cho bởi bảng:
Số công nhân (x) |
x1 = 35 |
x2 = 28 |
Thời gian xây xong nhà (y) |
y1 = 168 |
y2 = ? |
Ta có thời gian xây xong nhà (y) tỉ lệ nghịch với số công nhân làm việc theo hệ số tỉ lệ
a = x1 . y1 = 35 . 168 = 5 880.
Suy ra 28 . y2 = 5 880. Vì thế y2 = 5 880 : 28 = 210 (ngày)
Vậy 28 công nhân xây xong ngôi nhà trong 210 ngày.
Bài toán 2: Để tổ chức liên hoan cho gia đình, bác Ngọc dự định mua 2,9 kg thực phẩm gồm: thịt bò, thịt lợn, tôm sú. Số tiền bác Ngọc mua mỗi loại thực phẩm là như nhau. Biết giá thịt bò là 280 nghìn đồng/kg, giá thịt lợn là 160 nghìn đồng/kg và tôm sú là 320 nghìn đồng/kg. Mỗi loại thực phẩm bác Ngọc mua được là bao nhiêu kg?
Hướng dẫn giải
Gọi x (kg), y (kg), z (kg) lần lượt là số lượng thịt bò, thịt lợn, tôm sú mà bác Ngọc mua được. Khi đó: x + y + z = 2,9.
Vì số tiền mua mỗi loại thực phẩm là như nhau nên 280 . x = 160 . y = 320 . z
hay 7 . x = 4 . y = 8 . z (chia đồng thời các vế cho 40).
Do đó: .
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
.
Do đó:
(kg).
(kg).
(kg).
Vậy Bác Ngọc mua 0,8 kg thịt bò, 1,4 kg thịt lợn và 0,7 kg tôm sú.
Bài tập tổng hợp Toán 7 Chương 2
Bài 1: Chứng tỏ rằng:
a) 6 là căn bậc hai số học của 36.
b) –0,1 không phải là căn số học của 0,01.
Hướng dẫn giải
a) Ta có 6 ≥ 0 và 62 = 36 nên 6 là căn bậc hai số học của 36, ta viết .
b) Ta có (– 0,1)2 = 0,01 nhưng –0,1 < 0 nên – 0,1 không phải là căn bậc hai số học của 0,01.
Bài 2: Tìm giá trị của:
a) ;
b) .
Hướng dẫn giải
a) (vì ).
b) (vì (0,7)2 = 0,49).
Bài 3: Tính giá trị của biểu thức
a) ;
b) .
Hướng dẫn giải
a) Ta có và .
Nên .
b) Ta có và .
Nên .
Bài 4: Tìm số đối của mỗi số sau: ; 1,25 ; ; .
Hướng dẫn giải
Số đối của số thực là: .
Số đối của số thực 1,25 là –1,25.
Số đối của là .
Số đối của số thực là .
Bài 5: So sánh
a) và 2,142;
b) 3 và .
Hướng dẫn giải
a) Ta viết . Và so sánh với số 2,1420
Ta thấy kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần chục nghìn.
Do 8 > 0 nên 2,142857142857…> 2,1420. Vậy > 2,142.
b) Ta có 3 > 0 và 32 = 9 nên . Để so sánh 3 và ta sẽ so sánh và .
Ta có 9 > 8 > 0 nên > . Suy ra 3 > .
Bài 6: Tìm |–53|; ; .
Hướng dẫn giải
|–53| = –(–53) = 53
= =
= = .
Bài 7: Tính giá trị của biểu thức sau
a) |–100| – |34| ;
b) |12| + 3.|–8|.
Hướng dẫn giải
a) |–100| – |34| = 100 – 34 = 66.
b) |12| + 3. |–8| = 12 + 3.8 = 12 + 24 = 36.
Bài 8: Tìm x biết
a) |x| = 1 ;
b) |x – 3| = – 2 ;
c) |x + 0,5| = 4.
Hướng dẫn giải
a) |x| = 1 nên x = 1 hoặc x = –1.
b) | x – 3| ≥ 0 với mọi số thực x, nên không có số thực x nào thỏa mãn | x – 3| = –2
c) | x + 0,5| = 4 nên x + 0,5 = 4 hoặc x + 0,5 = –4
Với x + 0,5 = 4 thì x = 3,5
Với x + 0,5 = –4 thì x = –5,5.
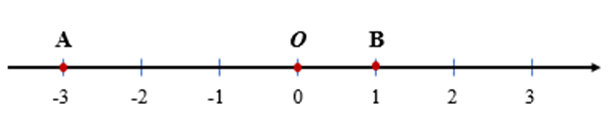
Bài 9: Tìm độ dài đoạn thẳng AB trong hình vẽ sau:
Hướng dẫn giải
Cách 1: Ta có AB = OA + OB = | –3| + |2| = 3 + 2 = 5
Cách 2 (Dùng chú ý ở trên): Ta có AB = | –3 – 2| = | –5| = 5.
Bài 10:
a) Làm tròn số 43 258 với độ chính xác 500;
b) Làm tròn số 81,934 với độ chính xác 0,5.
Hướng dẫn giải
a) Để làm tròn số 43 258 với độ chính xác 500 ta sẽ làm tròn đến hàng nghìn. Áp dụng quy tắc làm tròn số ta có 43 258 ≈ 43 000.
b) Để làm tròn số 81,934 với độ chính xác 0,5 ta sẽ làm tròn đến hàng đơn vị. Áp dụng quy tắc làm tròn số ta có 81, 934 ≈ 82.
Bài 11: Áp dụng quy tắc làm tròn số để ước lượng kết quả của mỗi phép tính sau
a) ( –34,17) + (– 65,83);
b) (– 19,641) . (–29,613).
Hướng dẫn giải
a) Ta làm tròn hai số hạng đến hàng phần mười ta có –34,17 ≈ –34,2; – 65,83 ≈ – 65,8.
Khi đó (–34,17) + (–65,83) ≈ (–34,2) + (–65,8) = –100.
b) Ta làm tròn hai thừa số đến hàng đơn vị, ta có: – 19,641 ≈ –20; –29,613 ≈ –30.
Vậy (– 19,641) . (–29,613) ≈ (–20).(–30) = 600.
Bài 12: Từ các tỉ số sau đây có lập được tỉ lệ thức hay không?
a) 2 : 3 và 14 : 21;
b) –7 : và 0,9 : (–0,5) .
Hướng dẫn giải
a) Ta có 14 : 21 =14 . = = .
Vậy từ hai tỉ số 2 : 3 và 14 : 21 ta lập được tỉ lệ thức.
b) Ta có ; 0,9 : (–0,5) = –1,8.
Do –1,5 ≠ –1,8 nên từ hai tỉ số –7 : và 0,9 : (–0,5) không lập được tỉ lệ thức.
Bài 13: Tìm x, biết
a) x : 8 = 3 : (–5);
b) .
Hướng dẫn giải
a) Từ x : 8 = 3 : (–5) ta có .
Do đó : – 5x = 8 . 3
Suy ra .
b) Từ suy ra .
Bài 14: Lập tất cả các tỉ lệ thức có được từ đẳng thức 7 . (–28) = (–49) . 4.
Hướng dẫn giải
Từ đẳng thức 7 . (–28) = (–49) . 4 ta lập được bốn tỉ lệ thức sau :
.
Bài 15: Tìm hai số x và y, biết: và x + y = 16.
Hướng dẫn giải
Áp dụng tính chất dãy tỉ số bằng nhau ta có: .
Vậy x = 3.2 = 6; y = 5.2 = 10.
Bài 16: Tìm hai số a và b, biết : a : 2 = b : (–5) và a – b = –7.
Hướng dẫn giải
Từ a : 2 = b : (–5) ta có tỉ lệ thức .
Áp dụng tính chất dãy tỉ số bằng nhau ta có: .
Vậy a = 2. (–1) = –2 ; b = (–5). (–1) = 5.
Bài 17: Một mảnh vườn hình chữ nhật với tỉ số giữa độ dài hai cạnh của nó bằng 3 : 5 và chu vi bằng 48 m. Tính diện tích mảnh vườn đó.
Hướng dẫn giải
Gọi độ dài hai cạnh của mảnh vườn hình chữ nhật lần lượt là a (mét) và b (mét).
Ta có và 2.(a + b) = 48 (chu vi hình chữ nhật bằng 48 m) nên a + b = 24.
Áp dụng tính chất dãy tỉ số bằng nhau ta có: .
Suy ra a = 3.3 = 9 ; b = 5 . 3 = 15.
Vậy diện tích của mảnh vườn là 9 . 15 = 135 (m2).
Bài 18: Cho biết x và y là hai đại lượng tỉ lệ thuận và khi x = 2 thì y = –4.
a) Tìm hệ số tỉ lệ của y đối với x.
b) Viết công thức tính y theo x.
c) Điền số thích hợp vào ô trống trong bảng sau :
x |
–3 |
–1 |
1 |
5 |
y |
Hướng dẫn giải
a) Gọi k là hệ số tỉ lệ của y đối với x. Ta có y = kx.
Vì khi x = 2 thì y = – 4 nên – 4 = k . 2 hay k = (–4) : 2 = –2.
b) Ta có y = –2x.
c) Khi x = –3 thì y = (–2) .( –3) = 6.
Khi x = –1 thì y = (–2).( –1) = 2.
Khi x = 1 thì y = (–2) . 1 = –2.
Khi x = 5 thì y = (–2) . 5 = –10.
Vậy ta có bảng :
x |
–3 |
–1 |
1 |
5 |
y |
6 |
2 |
–2 |
–10 |
Bài 19: 5 mét dây đồng nặng 43 gam. Hỏi 10 km dây đồng như thế nặng bao nhiêu kilogam ?
Hướng dẫn giải:
Gọi x (gam) và y (mét) lần lượt là khối lượng và chiều dài của dây đồng.
Đổi 10 km = 10 000m
Khi đó mối quan hệ giữa khối lượng (x) và chiều dài (y) được cho bởi bảng sau :
Khối lượng (x) |
x1 = 43 |
x2 = ? |
Chiều dài (y) |
y1 = 5 |
y2 = 10 000 |
Ta có chiều dài tỉ lệ thuận với khối lượng của dây theo hệ số tỉ lệ
Suy ra . Vì thế (gam) = 86 (kg)
Vậy 10km dây đồng nặng 86 kg.
Bài 20: Học sinh của ba lớp 7 cần trồng và chăm sóc 24 cây xanh. Lớp 7A có 32 học sinh, lớp 7B có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh, biết số cây xanh tỉ lệ thuận với số học sinh của lớp.
Hướng dẫn giải
Gọi số cây xanh mỗi lớp 7A, 7B, 7C cần trồng và chăm sóc lần lượt là x (cây), y (cây), z(cây).
Vì số cây tỉ lệ thuận với số học sinh của lớp nên ta có: và x + y + z = 24.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
.
Do đó x = 32 . 0,25 = 8
y = 28 . 0,25 = 7
z = 36 . 0,25 = 9
Vậy số cây mà mỗi lớp 7A, 7B, 7C cần trồng và chăm sóc lần lượt là 8 (cây); 7 (cây); 9 (cây).
Bài 21: Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 15 thì y = 8.
a) Tìm hệ số tỉ lệ;
b) Viết công thức y theo x;
c) Tính giá trị của y khi x = 6; x = 10.
Hướng dẫn giải
a) Ta có xy = 15 . 8 = 120 nên hệ số tỉ lệ là 120.
b) Do xy = 120 nên ta công thức biểu diễn y theo x là .
c) Khi x = 6 thì
Khi x = 10 thì .
Bài 22: Biết 3 người làm cỏ trên một cánh đồng hết 6 giờ. Hỏi 12 người (với cùng năng suất như thế) làm cỏ trên cánh đồng đó hết bao nhiêu thời gian ?
Hướng dẫn giải
Gọi x (người), y (giờ) lần lượt là số người và thời gian để số người đó hoàn thành việc làm cỏ trên cánh đồng. Khi đó ta có mỗi quan hệ giữa số người (x) và thời gian hoàn thành công việc (y) được cho bởi bảng sau :
Số người (x) |
x1 = 3 |
x2 = 12 |
Thời gian hoàn thành công việc (y) |
y1 = 6 |
y2 = ? |
Do thời gian hoàn thành công việc tỉ lệ nghịch với với số người làm việc theo hệ số tỉ lệ
a = x1. y1 = 3.6 = 18.
Suy ra 12 . y2 = 18. Vì thế y2 = 18 : 12 = 1,5.
Vậy 12 người hoàn thành công việc làm cỏ trong 1,5 giờ.
Bài 23: Một ô tô dự định đi từ A đến B trong 6 giờ. Nhưng thực tế ô tô đi với vận tốc gấp vận tốc dự định. Tính thời gian ô tô đã đi.
Hướng dẫn giải
Gọi t (h) là thời gian thực tế ô tô đã đi.
Vì vận tốc thực tế ô tô đi gấp vận tốc dự định nên tỉ lệ giữa vận tốc thực tế và vận tốc dự định là .
Mà vận tốc và thời gian ô tô đi trên quãng đường AB là hai đại lượng tỉ lệ nghịch nên
Do đó (h)
Vậy thời gian thực tế ô tô đã đi là 4,5 (h).
Học tốt Toán 7 Chương 2
Các bài học để học tốt Chương 2 Toán lớp 7 hay khác:
Xem thêm tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 7 hay khác:
- Giải sgk Toán 7 Cánh diều
- Giải SBT Toán 7 Cánh diều
- Giải lớp 7 Cánh diều (các môn học)
- Giải lớp 7 Kết nối tri thức (các môn học)
- Giải lớp 7 Chân trời sáng tạo (các môn học)
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giải bài tập Toán lớp 7 của chúng tôi được biên soạn bám sát sgk Toán 7 Tập 1 & Tập 2 bộ sách Cánh diều (NXB Đại học Sư phạm).
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 7 (hay nhất) - Cánh diều
- Soạn văn 7 (ngắn nhất) - Cánh diều
- Giải sgk Toán 7 - Cánh diều
- Giải Tiếng Anh 7 Global Success
- Giải Tiếng Anh 7 Friends plus
- Giải sgk Tiếng Anh 7 Smart World
- Giải Tiếng Anh 7 Explore English
- Giải sgk Khoa học tự nhiên 7 - Cánh diều
- Giải sgk Lịch Sử 7 - Cánh diều
- Giải sgk Địa Lí 7 - Cánh diều
- Giải sgk Giáo dục công dân 7 - Cánh diều
- Giải sgk Công nghệ 7 - Cánh diều
- Giải sgk Tin học 7 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 7 - Cánh diều
- Giải sgk Âm nhạc 7 - Cánh diều

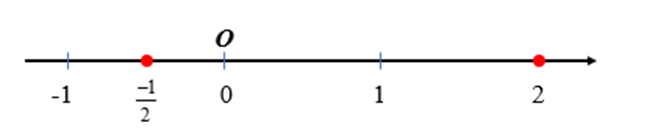








 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

