Tổng hợp lý thuyết Toán 7 Chương 5 Cánh diều

Với Tổng hợp lý thuyết Toán 7 Chương 5: Một số yếu tố thống kê và xác suất sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tổng hợp lý thuyết Toán 7 Chương 5 Cánh diều

Lý thuyết tổng hợp Toán 7 Chương 5

1. Thu thập và phân loại dữ liệu

Trong các dữ liệu thống kê thu thập được, có những dữ liệu thống kê là số (số liệu) nhưng cũng có những dữ liệu thống kê không phải là số.

Ví dụ:

+ Cân nặng (đơn vị: kg) của 10 bạn học sinh tổ 1 của lớp 7A lần lượt là: 45; 39; 52; 63; 48; 47; 49; 51; 60; 40.

Đây là dãy số liệu.

+ Tên 4 loại phương tiện chạy trên mặt đất đang có hiện nay là: xe đạp, xe máy, xe ô tô, xe buýt.

Đây không phải là dãy số liệu.

+ Các mức độ yêu thích trò chơi cờ vua là: Rất thích; Thích; Bình thường; Không thích; Không quan tâm.

Đây không phải là dãy số liệu.

2. Tính hợp lí của dữ liệu

Sau khi thu thập, tổ chức, phân loại dữ liệu, ta cần xem xét tính hợp lí của những dữ liệu thống kê đó, đặc biệt chỉ ra được những dữ liệu không hợp lí. Ta có thể dựa trên những tiêu chí toán học đơn giản để thực hiện điều đó.

Ví dụ: Để hưởng ứng chương trình “Hỗ trợ các bạn dân tộc miền núi”, mỗi bạn học sinh trong lớp 7A đóng góp 3 quyển vở trắng. Bạn lớp trưởng lớp 7A đã ghi lại số liệu như bảng sau:

Biết rằng bạn lớp trưởng đã ghi nhầm số liệu của một tổ trong bảng trên. Theo em, bạn lớp trưởng đã ghi nhầm số liệu của tổ nào?

Hướng dẫn giải

Số quyển vở trắng tổ 1 đóng góp được là: 9.3 = 27 (quyển).

Số quyển vở trắng tổ 2 đóng góp được là: 10.3 = 30 (quyển).

Số quyển vở trắng tổ 3 đóng góp được là: 9.3 = 27 (quyển).

Số quyển vở trắng tổ 4 đóng góp được là: 10.3 = 30 (quyển).

Theo tính toán, tổ 3 chỉ đóng góp được 27 quyển vở trắng nhưng bạn lớp trưởng ghi trong bảng là 30 quyển.

Vậy bạn lớp trưởng đã ghi nhầm số liệu của tổ 3.

3. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ

Ở lớp 6, chúng ta đã làm quen với việc mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ (bảng số liệu, biểu đồ tranh, biểu đồ cột, biểu đồ cột kép).

Ở lớp 7, chúng ta tiếp tục tìm hiểu sâu hơn việc đọc hiểu, rút ra những thông tin cần thiết từ những dạng biểu diễn dữ liệu đã học và nhận biết những dạng biểu diễn khác nhau cho một tập dữ liệu.

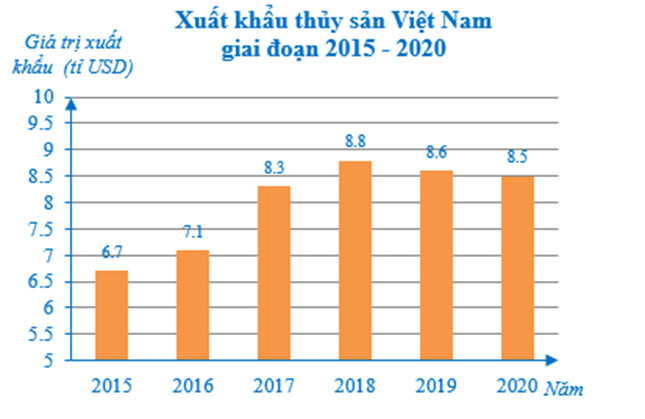
Ví dụ: Biểu đồ hình cột thể hiện tình hình xuất khẩu thủy sản Việt Nam giai đoạn 2015 – 2020:

a) Nêu cách xác định giá trị xuất khẩu thủy sản Việt Nam trong mỗi năm từ năm 2015 đến năm 2020.

b) Lập bảng số liệu thống kê tình hình xuất khẩu thủy sản Việt Nam giai đoạn 2015 – 2020 (đơn vị: tỉ USD).

Hướng dẫn giải

a) Để xác định giá trị xuất khẩu thủy sản Việt Nam trong mỗi năm từ năm 2015 đến năm 2020, ta thực hiện như sau:

Nhìn vào cột biểu thị giá trị xuất khẩu thủy sản Việt Nam trong năm 2015 ở biểu đồ trên, ta thấy trên đỉnh cột đó có ghi số 6,7 và đơn vị tính ghi trên trục thẳng đứng là tỉ USD.

Vậy giá trị xuất khẩu thủy sản Việt Nam trong năm 2015 là 6,7 tỉ USD.

Tương tự như trên, ta xác định được giá trị xuất khẩu thủy sản Việt Nam trong mỗi năm còn lại:

+ Năm 2016: 7,1 tỉ USD;

+ Năm 2017: 8,3 tỉ USD;

+ Năm 2018: 8,8 tỉ USD;

+ Năm 2019: 8,6 tỉ USD;

+ Năm 2020: 8,5 tỉ USD.

Vậy giá trị xuất khẩu thủy sản Việt Nam trong mỗi năm 2015; 2016; 2017; 2018; 2019; 2020 lần lượt là: 6,7 tỷ USD; 7,1 tỷ USD; 8,3 tỷ USD; 8,8 tỷ USD; 8,6 tỷ USD; 8,5 tỷ USD.

b) Ta có bảng số liệu sau:

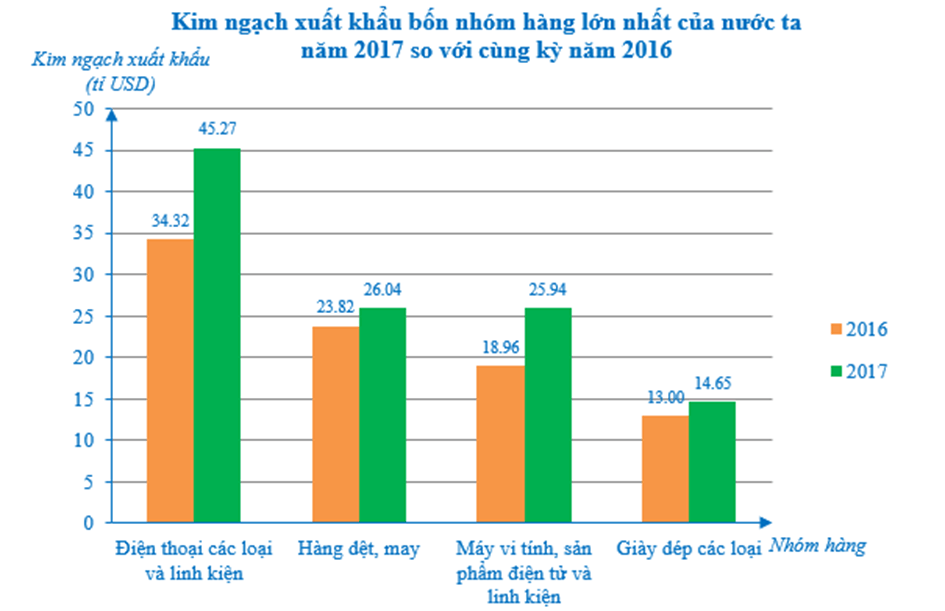
Ví dụ: Biểu đồ sau đây cho biết kim ngạch xuất khẩu bốn nhóm hàng lớn nhất của nước ta năm 2017 so với cùng kỳ năm 2016.

a) Nêu cách xác định kim ngạch xuất khẩu ở mỗi nhóm hàng trong bốn nhóm hàng lớn nhất của nước ta năm 2016.

b) Nêu cách xác định kim ngạch xuất khẩu ở mỗi nhóm hàng trong bốn nhóm hàng lớn nhất của nước ta năm 2017.

c) Lập bảng số liệu thống kê kim ngạch xuất khẩu bốn nhóm hàng lớn nhất của nước ta năm 2017 so với cùng kỳ năm 2016 theo mẫu sau (đơn vị: tỉ USD):

Hướng dẫn giải

a) Nhìn vào cột (màu cam) của biểu đồ trên biểu thị kim ngạch xuất khẩu ở nhóm hàng Điện thoại các loại và linh kiện của nước ta năm 2016, ta thấy trên đỉnh cột đó ghi số 34,32 và đơn vị tính ghi trên trục thẳng đứng là tỉ USD.

Vậy kim ngạch xuất khẩu ở nhóm hàng Điện thoại các loại và linh kiện của nước ta năm 2016 là 34,32 tỉ USD.

Tương tự như trên, ta xác định được kim ngạch xuất khẩu của nước ta trong các nhóm hàng Hàng dệt, may; Máy vi tính, sản phẩm điện tử và linh kiện; Giày dép các loại năm 2016 lần lượt là: 23,82; 18,96; 13,00 (tỉ USD).

Vậy kim ngạch xuất khẩu của nước ta trong các nhóm hàng Điện thoại các loại và linh kiện; Hàng dệt, may; Máy vi tính, sản phẩm điện tử và linh kiện; Giày dép các loại năm 2016 lần lượt là: 34,32 tỉ USD; 23,82 tỉ USD; 18,96 tỉ USD; 13,00 tỉ USD.

b) Nhìn vào cột (màu xanh) của biểu đồ trên biểu thị kim ngạch xuất khẩu ở nhóm hàng Điện thoại các loại và linh kiện của nước ta năm 2017, ta thấy trên đỉnh cột đó ghi số 45,27 và đơn vị tính ghi trên trục thẳng đứng là tỉ USD.

Vậy kim ngạch xuất khẩu ở nhóm hàng điện thoại các loại và linh kiện của nước ta năm 2017 là 45,27 tỉ USD.

Tương tự như trên, ta xác định được kim ngạch xuất khẩu của nước ta trong các nhóm hàng Hàng dệt, may; Máy vi tính, sản phẩm điện tử và linh kiện; Giày dép các loại năm 2017 lần lượt là: 26,04 tỉ USD; 25,94 tỉ USD; 14,65 tỉ USD.

Vậy kim ngạch xuất khẩu của nước ta trong các nhóm hàng điện thoại các loại và linh kiện ; hàng dệt, may; máy vi tính, sản phẩm điện tử và linh kiện; giày dép các loại năm 2016 lần lượt là: 45,27 tỉ USD; 26,04 tỉ USD; 25,94 tỉ USD; 14,65 tỉ USD.

c) Ta có bảng số liệu sau:

4. Phân tích và xử lí dữ liệu để rút ra kết luận

Sau khi thu thập, tổ chức, phân loại, biểu diễn dữ liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận. Thông thường, quá trình phân tích và xử lí dữ liệu dựa trên tính toán và suy luận toán học.

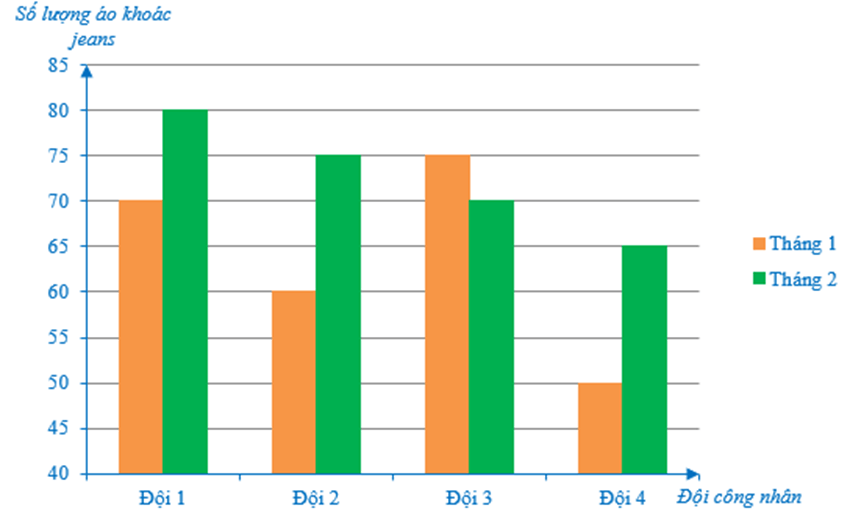
Ví dụ: Một công ty gồm có bốn đội công nhân may áo khoác jeans. Năng suất may được số lượng áo khoác jeans của bốn đội công nhân đó trong 2 tháng đầu năm được biểu diễn như trong biểu đồ sau:

a) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn.

b) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn.

c) Đội công nhân nào may được nhiều nhất ở mỗi tháng?

d) Đội công nhân nào may được ít nhất ở mỗi tháng?

e) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được nhiều nhất?

f) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được ít nhất?

Hướng dẫn giải

a) Ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 2; Đội 1; Đội 3.

b) Ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 3; Đội 2; Đội 1.

c) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 3 may được nhiều áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 1 may được nhiều áo khoác jeans nhất.

Vậy đội công nhân may được nhiều áo khoác jeans nhất ở tháng 1, tháng 2 lần lượt là Đội 3 và Đội 1.

d) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 4 may được ít áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 4 may được ít áo khoác jeans nhất.

Vậy đội công nhân may được ít áo khoác jeans nhất ở tháng 1, tháng 2 đều là Đội 4.

e) Tổng số áo khoác jeans Đội 1 may được ở cả hai tháng là:

70 + 80 = 150 (áo khoác jeans).

Tổng số áo khoác jeans Đội 2 may được ở cả hai tháng là:

60 + 75 = 135 (áo khoác jeans).

Tổng số áo khoác jeans Đội 3 may được ở cả hai tháng là:

75 + 70 = 145 (áo khoác jeans).

Tổng số áo khoác jeans Đội 4 may được ở cả hai tháng là:

50 + 65 = 115 (áo khoác jeans).

Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 1 có tổng số áo sơ mi may được nhiều nhất.

f) Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 4 có tổng số áo sơ mi may được ít nhất.

5. Tính hợp lí của kết luận thống kê

Quá trình phân tích và xử lí dữ liệu giúp chúng ta có thể nhận biết được: tính hợp lí của dữ liệu thống kê, tính hợp lí của kết luận thống kê và ta cũng có thể bác bỏ kết luận đã nêu ra. Thông thường, để làm được điều đó ta dựa trên những tiêu chí đơn giản hoặc dựa trên tính toán và suy luận toán học.

Ví dụ: Một huấn luyện viên dạy bơi sải ghi lại thời gian (tính theo buổi, mỗi buổi 90 phút) thành thạo môn bơi sải của các học viên như bảng bên:

a) Huấn luyện viên đã khảo sát tổng cộng bao nhiêu học viên?

b) Biết rằng học viên có năng khiếu về môn bơi lội sẽ thành thạo bơi sải trong vòng 8 buổi học. Huấn luyện viên đã đưa ra kết luận rằng: Sau khi khảo sát, số học viên có năng khiếu về môn bơi lội chiếm tỉ lệ 15% so với tổng số học viên tham gia khảo sát. Hỏi kết luận đó của huấn luyện viên có đúng không?

Hướng dẫn giải

a) Số học viên mà huấn luyện viên đã khảo sát là:

1 + 2 + 3 + 10 + 13 + 7 + 4 = 40 (học viên).

Vậy huấn luyện viên đã khảo sát tổng cộng là 40 học viên.

b) Số học viên được huấn luyện viên đánh giá là có năng khiếu về môn bơi lội là:

1 + 2 + 3 = 6 (học viên).

So với tổng số học viên tham gia khảo sát, tỉ lệ học viên được đánh giá là có năng khiếu về môn bơi lội là:

$\frac{6.100}{40}\%=15\%$.

Vậy huấn luyện viên đã kết luận đúng.

6. Biểu đồ đoạn thẳng

Biểu đồ đoạn thẳng có các yếu tố sau:

+ Trục nằm ngang biểu diễn các đối tượng thống kê;

+ Trục thẳng đứng biểu diễn tiêu chí thống kê và trên trục đó đã xác định độ dài đơn vị thống kê;

+ Biểu đồ đoạn thẳng là đường gấp khúc nối từng điểm liên tiếp bằng các đoạn thẳng;

+ Mỗi điểm đầu mút của các đoạn thẳng trong đường gấp khúc được xác định bởi một đối tượng thống kê và số liệu thống kê theo tiêu chí của đối tượng đó.

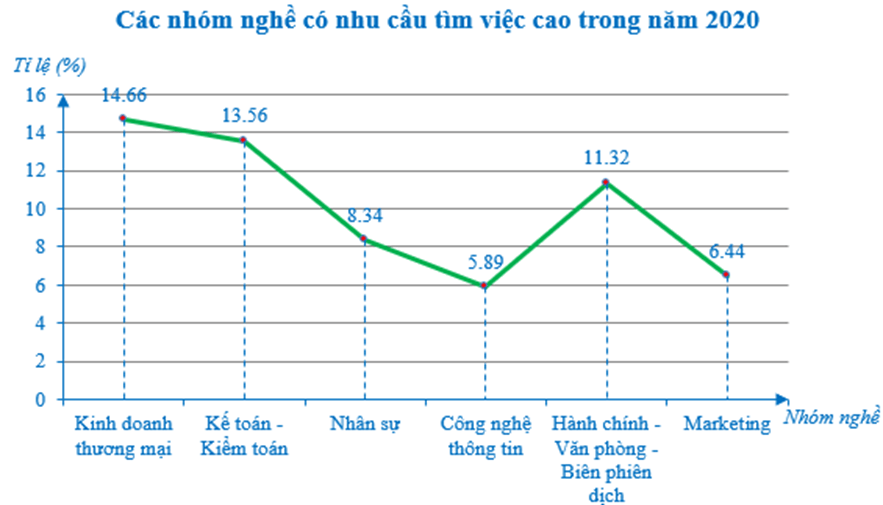
Ví dụ: Cho biểu đồ đoạn thẳng sau thể hiện các nhóm nghề có nhu cầu tìm việc cao tại Thành phố Hồ Chí Minh trong năm 2020 (đơn vị: %):

Ở biểu đồ trên, ta có:

+ Trục nằm ngang biểu diễn các đối tượng thống kê là các nhóm nghề bao gồm: Kinh doanh thương mại; Kế toán – Kiểm toán; Nhân sự; Công nghệ thông tin; Hành chính – Văn phòng – Biên phiên dịch; Marketing;

+ Trục thẳng đứng biểu diễn tiêu chí thống kê là tỉ lệ (tính theo %) nhu cầu tìm việc của các nhóm nghề nêu trên;

+ Đường gấp khúc gồm các đoạn thẳng nối liền liên tiếp 6 điểm. Mỗi điểm được xác định bởi nhóm nghề và tỉ lệ nhu cầu tìm việc của nhóm nghề đó.

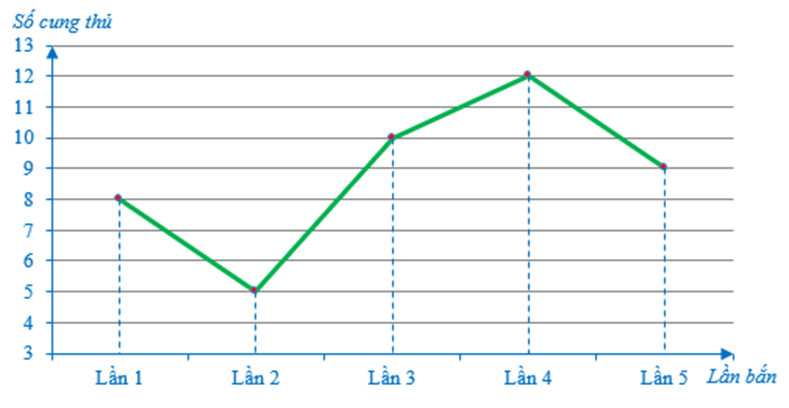
Ví dụ: Biểu đồ sau đây cho biết số cung thủ bắn trúng tâm đỏ trong năm lần bắn liên tiếp.

Nêu số cung thủ bắn trúng tâm đỏ trong từng lần bắn của các cung thủ.

Hướng dẫn giải

Để biết số cung thủ bắn trúng tâm đỏ trong từng lần bắn, ta làm như sau:

+ Từ điểm “Lần 1” trên trục nằm ngang, dóng theo chiều thẳng đứng tới đầu mút của đoạn thẳng thuộc đường gấp khúc;

+ Đi tiếp theo chiều ngang về bên trái cho đến khi gặp trục thẳng đứng;

+ Đọc chỉ số trên trục thẳng đứng.

Ta có: Số cung thủ bắn trúng tâm đỏ trong lần 1 là 8 (cung thủ).

Tương tự như trên, số cung thủ bắn trúng tâm đỏ trong lần 2, lần 3, lần 4, lần 5 lần lượt là: 5; 10; 12; 9 (cung thủ).

Vậy số cung thủ bắn trúng tâm đỏ trong lần 1, lần 2, lần 3, lần 4, lần 5 lần lượt là 8; 5; 10; 12; 9 (cung thủ).

Chú ý:

+ Cũng như biểu đồ cột và biểu đồ cột kép, biểu đồ đoạn thẳng giúp chúng ta “trực quan hóa” một tập dữ liệu thống kê thông qua cách biểu diễn hình học tập dữ liệu đó.

+ Người ta còn biểu diễn dữ liệu thống kê ở dạng biểu đồ tương tự biểu đồ cột, trong đó các cột được thay bằng các đoạn thẳng. Biểu đồ đó cũng gọi là biểu đồ đoạn thẳng.

Chẳng hạn như biểu đồ dưới đây:

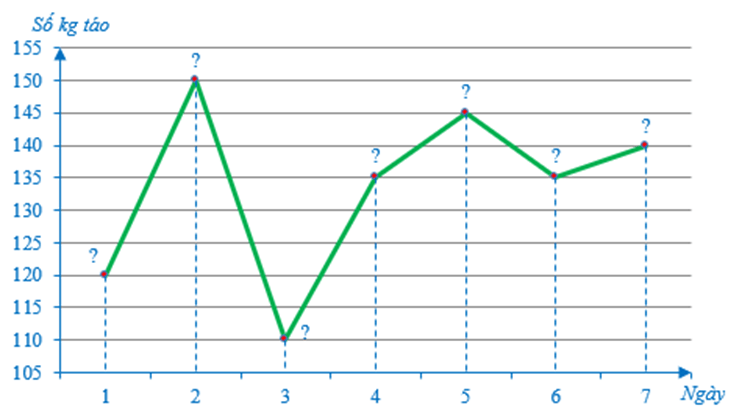
Ví dụ: Để theo dõi lượng táo mà đội hái trái cây hái được mỗi ngày trong một tuần, người chủ nông trại đã kiểm đếm (tính theo đơn vị kg) mỗi ngày và ghi lại như bảng sau:

Chọn số liệu thích hợp để điền vào dấu “?” trong biểu đồ sau:

Hướng dẫn giải

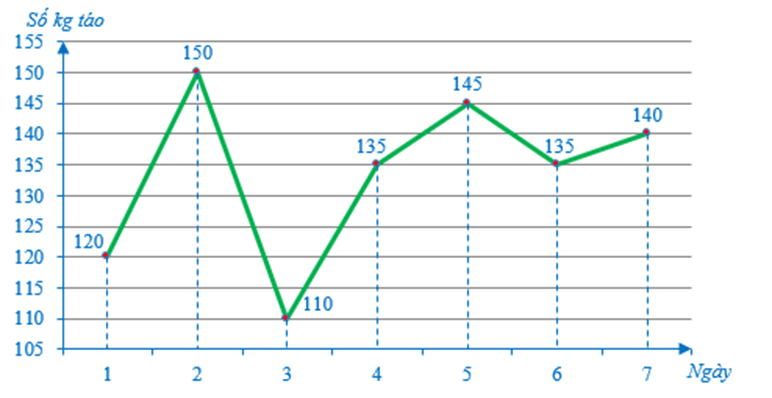
Sau khi hoàn thiện các số liệu vào biểu đồ, ta nhận được biểu đồ sau biểu diễn số kg táo đội hái trái cây hái được trong một tuần mà chủ nông trại kiểm đếm:

Nhận xét: Như ta đã biết, dữ liệu thống kê có thể biểu diễn ở những dạng khác nhau, trong đó có biểu đồ đoạn thẳng.

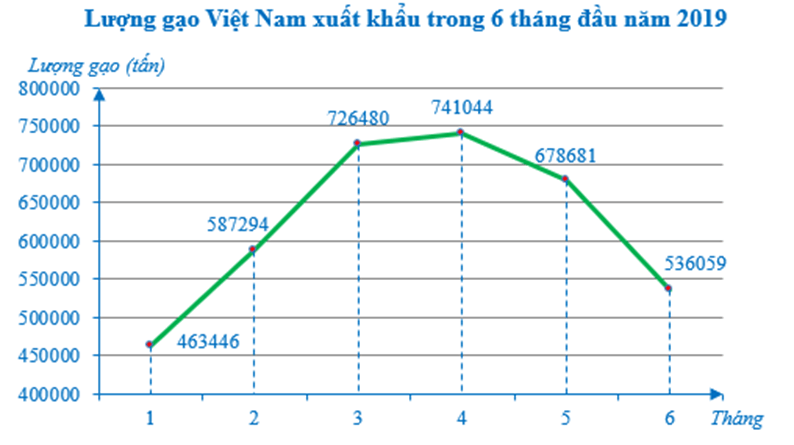
Ví dụ: Biểu đồ sau đây thể hiện lượng gạo Việt Nam xuất khẩu trong 6 tháng đầu năm 2019:

Lập bảng số liệu thống kê lượng gạo Việt Nam xuất khẩu năm 2019.

Hướng dẫn giải

Từ biểu đồ trên, ta có bảng số liệu sau:

7. Phân tích và xử lí dữ liệu biểu diễn bằng biểu đồ đoạn thẳng

Dựa vào biểu đồ đoạn thẳng, ta có thể xác định xu hướng tăng hoặc giảm của tập số liệu trong một khoảng thời gian nhất định.

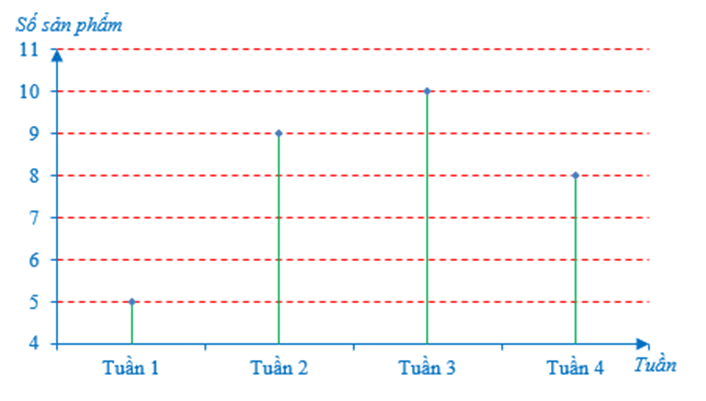
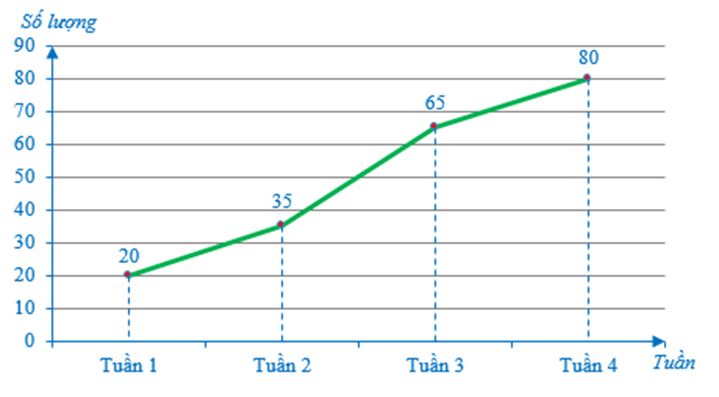
Ví dụ: Một cửa hàng bán điện thoại smartphone đã thống kê lại số lượng điện thoại smartphone bán được mỗi tuần của tháng 2 năm 2021 như biểu đồ bên dưới.

a) Lập bảng số liệu thống kê số lượng điện thoại smartphone cửa hàng đã bán được mỗi tuần của tháng 2 năm 2021.

b) Trong 4 tuần đó, tuần nào cửa hàng bán được nhiều điện thoại nhất?

c) Số lượng điện thoại bán được ở tuần 3 tăng bao nhiêu phần trăm so với tuần 2 (làm tròn kết quả đến hàng phần trăm)?

d) Dựa vào biểu đồ đoạn thẳng, nêu nhận xét về số lượng điện thoại smartphone cửa hàng đã bán được trong tháng 2 năm 2021.

Hướng dẫn giải

a) Từ biểu đồ trên, ta có bảng số liệu sau:

b) Trong 4 tuần đó, tuần 4 cửa hàng bán được nhiều điện thoại nhất với số lượng điện thoại smartphone bán được là 80 điện thoại.

c) Tỉ số phần trăm của số lượng điện thoại bán được ở tuần 3 và số lượng điện thoại bán được ở tuần 2 là:

$\frac{65.100}{35}\%\approx \mathrm{185,71}\%$.

Vậy số lượng điện thoại bán được ở tuần 3 đã tăng 185,71% – 100% = 85,71% so với tuần 2.

d) Dựa vào biểu đồ đoạn thẳng, ta thấy số lượng điện thoại cửa hàng bán được liên tục tăng trong tháng 2 năm 2021.

8. Biểu đồ hình quạt tròn

Biểu đồ hình quạt tròn có các yếu tố sau:

+ Đối tượng thống kê được biểu diễn bằng các hình quạt tròn.

+ Số liệu thống kê theo tiêu chí thống kê của mỗi đối tượng (thống kê) được ghi ở hình quạt tròn tương ứng. Số liệu thống kê đó được tính theo tỉ số phần trăm.

+ Tổng các tỉ số phần trăm ghi ở các hình quạt tròn là 100%, nghĩa là tổng các tỉ số phần trăm của các số liệu thành phần phải bằng 100% (của tổng thể thống kê).

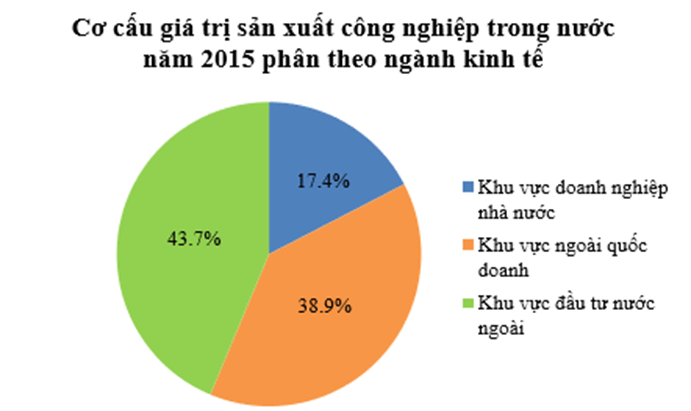
Ví dụ: Biểu đồ sau thể hiện cơ cấu giá trị sản xuất công nghiệp trong nước năm 2015 phân theo ngành kinh tế (tính theo đơn vị %):

Ở biểu đồ trên, ta có:

+ Đối tượng và tiêu chí thống kê: cơ cấu giá trị sản xuất công nghiệp trong nước năm 2015 phân theo ngành kinh tế (Khu vực doanh nghiệp nhà nước, Khu vực ngoài quốc doanh, Khu vực đầu tư nước ngoài) và được biểu diễn bởi ba hình quạt tròn.

+ Số liệu thống kê theo tiêu chí thống kê của mỗi đối tượng (thống kê): biểu diễn bởi tỉ số phần trăm ghi ở mỗi hình quạt tròn, tương ứng với cơ cấu giá trị sản xuất công nghiệp trong nước phân theo ngành kinh tế.

+ Tổng ba tỉ số phần trăm ghi ở ba hình quạt tròn là: 23,5% + 32,2% + 44,3% = 100%, nghĩa là tổng các tỉ số phần trăm của các số liệu thành phần phải bằng 100% (của tổng thể thống kê).

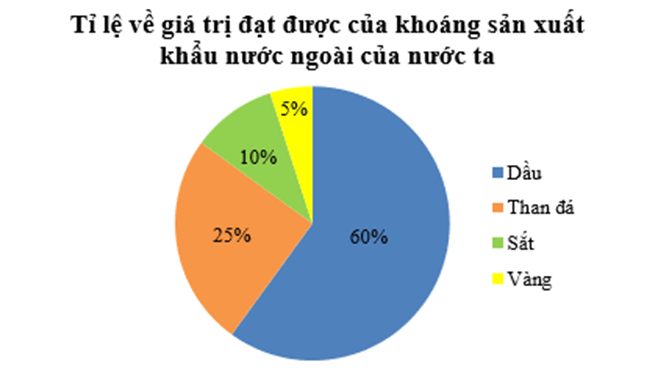
Ví dụ: Tỉ lệ về giá trị đạt được của khoáng sản xuất khẩu nước ngoài của nước ta (tính theo tỉ số phần trăm) như sau:

+ Dầu: 60%;

+ Than đá: 25%;

+ Sắt: 10%;

+ Vàng: 5%.

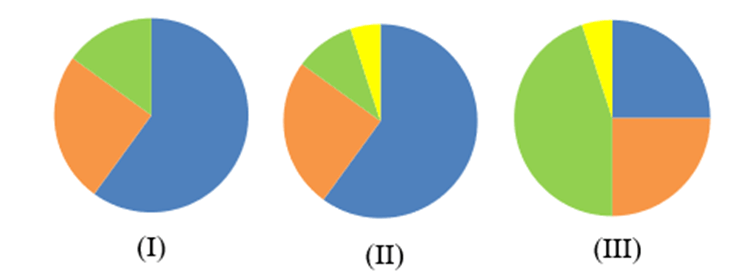
a) Trong các biểu đồ sau đây, ta có thể biểu diễn số liệu đã cho trên biểu đồ nào để nhận được biểu đồ hình quạt tròn thống kê các tỉ lệ về giá trị đạt được của khoáng sản xuất khẩu nước ngoài của nước ta?

b) Tỉ lệ về giá trị đạt được của dầu và than đá chiếm tổng cộng bao nhiêu phần trăm?

c) Tỉ lệ về giá trị đạt được của than đá gấp bao nhiêu lần tỉ lệ về giá trị đạt được của vàng?

Hướng dẫn giải

a) Ta có tất cả 4 loại khoáng sản (dầu, than đá, sắt, vàng) và các loại khoáng sản đó có tỉ lệ phần trăm khác nhau nên chỉ có hình (II) phù hợp để biểu diễn các số liệu trên.

Sau khi biểu diễn, ta nhận được biểu đồ sau thống kê tỉ lệ về giá trị đạt được của khoáng sản xuất khẩu nước ngoài của nước ta:

b) Tỉ lệ về giá trị đạt được của dầu và than đá chiếm tổng cộng 60% + 25% = 85% (tổng lượng khoáng sản xuất khẩu của nước ta).

Vậy tỉ lệ về giá trị đạt được của dầu và than đá chiếm tổng cộng 85% so với tổng lượng khoáng sản xuất khẩu của nước ta.

c) Ta có 25% : 5% = 5.

Vậy tỉ lệ về giá trị đạt được của than đá gấp 5 lần tỉ lệ về giá trị đạt được của vàng.

Nhận xét: Như ta đã biết, dữ liệu thống kê có thể biểu diễn ở những dạng khác nhau, trong đó có biểu đồ hình quạt tròn.

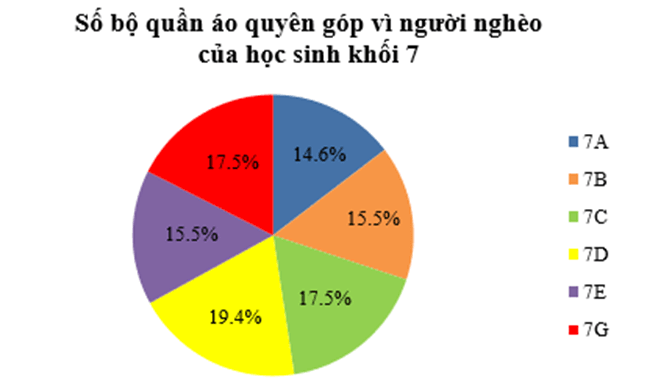
Ví dụ: Biểu đồ sau cho biết kết quả thống kê (tính theo tỉ số phần trăm) về số bộ quần áo quyên góp vì người nghèo của học sinh khối 7 tại một trường trung học cơ sở.

a) Lập bảng số liệu thống kê tỉ lệ số bộ quần áo quyên góp vì người nghèo của học sinh khối 7 theo mẫu sau:

b) Biết rằng khối 7 của trường đó đóng góp được 515 bộ quần áo. Lập bảng thống kê số quần áo mỗi lớp quyên góp được theo mẫu sau (làm tròn kết quả đến hàng đơn vị):

Hướng dẫn giải

a) Từ biểu đồ đã cho, ta có bảng sau:

b) Số bộ quần áo lớp 7A quyên góp là:

$\frac{\mathrm{515.14,6}}{100}=\mathrm{75,19}\approx 75$ (bộ quần áo).

Số bộ quần áo lớp 7B quyên góp là:

$\frac{\mathrm{515.15,5}}{100}=\mathrm{79,825}\approx 80$ (bộ quần áo).

Số bộ quần áo lớp 7C quyên góp là:

$\frac{\mathrm{515.17,5}}{100}=\mathrm{90,125}\approx 90$ (bộ quần áo).

Số bộ quần áo lớp 7D quyên góp là:

$\frac{\mathrm{515.19,4}}{100}=\mathrm{99,91}\approx 100$ (bộ quần áo).

Số bộ quần áo lớp 7E quyên góp là:

$\frac{\mathrm{515.15,5}}{100}=\mathrm{79,825}\approx 80$ (bộ quần áo).

Số bộ quần áo lớp 7G quyên góp là:

$\frac{\mathrm{515.17,5}}{100}=\mathrm{90,125}\approx 90$ (bộ quần áo).

Vậy ta có bảng số liệu thống kê sau:

Nhận xét:

Thông thường, trong bảng số liệu, ta có thể nhận biết nhanh chóng số liệu thống kê (theo tiêu chí) của mỗi đối tượng thống kê nhưng không biết được mỗi đối tượng đó chiếm bao nhiêu phần trăm trong tổng thể thống kê.

Ngược lại, trong biểu đồ hình quạt tròn, ta có thể nhận biết nhanh chóng mỗi đối tượng thống kê chiếm bao nhiêu phần trăm trong tổng thể thống kê nhưng lại không biết được số liệu thống kê (theo tiêu chí) của mỗi đối tượng đó.

Vì thế, tùy theo mục đích thống kê, ta sẽ lựa chọn bảng số liệu hay biểu đồ hình quạt trong để biểu diễn dữ liệu thống kê.

9. Phân tích và xử lí dữ liệu biểu diễn bằng biểu đồ hình quạt tròn

Dựa trên việc biểu diễn dữ liệu bằng biểu đồ hình quạt tròn, ta có thể phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận.

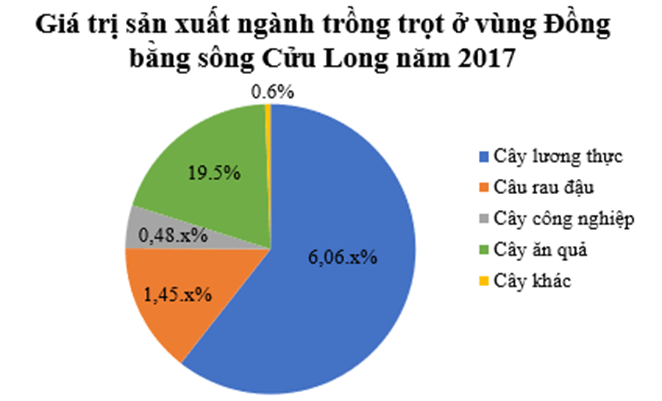
Ví dụ: Biểu đồ hình quạt tròn sau đây biểu diễn giá trị sản xuất ngành trồng trọt ở vùng Đồng bằng sông Cửu Long năm 2017:

a) Tính giá trị của x.

b) Tính tỉ số phần trăm sản lượng của cây lương thực, cây rau đậu và cây công nghiệp so với tổng sản lượng ngành trồng trọt của nước ta.

c) Cây lương thực và cây công nghiệp chiếm tổng cộng bao nhiêu phần trăm?

d) Cây lương thực và cây công nghiệp gấp khoảng bao nhiêu lần cây ăn quả (làm tròn đến hàng phần mười)?

e) Giả sử năm 2017, sản lượng cây rau đậu ở vùng Đồng bằng sông Cửu Long đạt khoảng 4,9 triệu tấn. Hoàn thành bảng số liệu sau (làm tròn đến hàng phần trăm):

Hướng dẫn giải

a) Ta có 6,06.x% + 1,45.x% + 0,48.x% + 19,5% + 0,6% = 100%.

Suy ra 7,99.x% + 20,1% = 100%.

Do đó 7,99.x% = 100% – 20,1%.

Khi đó 7,99.x% = 79,9%.

Vì vậy x% = 79,9% : 7,99.

Do đó x% = 10%.

Vậy x = 10.

b) Tỉ số phần trăm sản lượng của cây lương thực so với tổng sản lượng ngành trồng trọt của nước ta là: 6,06.10% = 60,6%.

Tỉ số phần trăm sản lượng của cây rau đậu so với tổng sản lượng ngành trồng trọt của nước ta là: 1,45.10% = 14,5%.

Tỉ số phần trăm sản lượng của cây công nghiệp so với tổng sản lượng ngành trồng trọt của nước ta là: 0,48.10% = 4,8%.

Vậy tỉ số phần trăm sản lượng của cây lương thực, cây rau đậu và cây công nghiệp so với tổng sản lượng ngành trồng trọt của nước ta lần lượt là 60,6%; 14,5%; 4,8%.

c) Cây lương thực và cây công nghiệp chiếm tổng cộng 60,6% + 4,8% = 65,4%.

Vậy cây lương thực và cây công nghiệp chiếm tổng cộng 65,4%.

d) Ta có 65,4% : 19,5% ≈ 3,4.

Vậy cây lương thực và cây công nghiệp gấp khoảng 3,4 lần cây ăn quả.

e) Vì 4,9 triệu tấn sản lượng cây rau đậu chiếm 14,5% tổng sản lượng ngành trồng trọt ở vùng Đồng bằng sông Cửu Long.

Nên 1% sản lượng cây rau đậu có sản lượng là khoảng:

4,9 : 14,5 ≈ 0,34 (triệu tấn).

Sản lượng cây lương thực trong tổng sản lượng ngành trồng trọt của nước ta là khoảng:

0,34.60,6 = 20,604 ≈ 20,6 (triệu tấn).

Sản lượng cây công nghiệp trong tổng sản lượng ngành trồng trọt của nước ta là khoảng:

0,34.4,8 = 1,632 ≈ 1,63 (triệu tấn).

Sản lượng cây ăn quả trong tổng sản lượng ngành trồng trọt của nước ta là khoảng:

0,34.19,5 = 6,63 (triệu tấn).

Sản lượng cây khác trong tổng sản lượng ngành trồng trọt của nước ta là khoảng:

0,34.0,6 = 0,204 ≈ 0,2 (triệu tấn).

Vậy ta có bảng số liệu thống kê sau:

10. Biến cố trong trò chơi gieo xúc xắc

Trong trò chơi gieo xúc xắc, ta quy ước xúc xắc là cân đối và đồng chất.

Mỗi xúc xắc có sáu mặt, số chấm ở mỗi mặt là một trong các số 1; 2; 3; 4; 5; 6. Gieo ngẫu nhiên xúc xắc một lần.

Nhận xét:

+ Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:

A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.

+ Tập hợp các kết quả có thể xảy ra đối với sự kiện “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” là: B = {mặt 2 chấm; mặt 4 chấm; mặt 6 chấm} (gồm ba phần tử lấy ra từ tập hợp A).

+ Trong trò chơi gieo xúc xắc, sự kiện “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” còn gọi là biến cố, hay gọi đầy đủ là biến cố ngẫu nhiên. Sở dĩ ta có thêm cụm từ “ngẫu nhiên” là vì các kết quả xảy ra có tính ngẫu nhiên, ta không thể đoán trước được.

+ Mỗi kết quả: mặt 2 chấm, mặt 4 chấm, mặt 6 chấm (là phần tử của tập hợp B), được gọi là một kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn”. Sở dĩ ta gọi những kết quả đó là thuận lợi cho biến cố trên vì chúng đáp ứng được mong muốn thể hiện trong biến cố, đó là mặt xuất hiện có số chấm là số chẵn.

Ví dụ: Gieo ngẫu nhiên xúc xắc một lần. Xét biến cố “Mặt xuất hiện của xúc xắc có số chấm là các số nhỏ hơn 5”.

a) Viết tập hợp A gồm các kết quả có thể xảy ra khi với mặt xuất hiện của xúc xắc.

b) Viết tập hợp M gồm các kết quả có thể xảy ra đối với biến cố trên.

c) Nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:

A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.

b) Trong các số 1; 2; 3; 4; 5; 6, các số nhỏ hơn 5 là: 1; 2; 3; 4.

Các kết quả có thể xảy ra đối với biến cố “Mặt xuất hiện của xúc xắc có số chấm là các số nhỏ hơn 5” là: mặt 1 chấm; mặt 2 chấm; mặt 3 chấm và mặt 4 chấm (gồm bốn phần tử lấy ra từ tập hợp A).

Tập hợp M gồm các kết quả có thể xảy ra đối với biến cố trên là:

M = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm}.

c) Có bốn kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là các số nhỏ hơn 5” là: mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm (lấy ra từ tập hợp A).

11. Biến cố trong trò chơi rút thẻ từ trong hộp

Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

Nhận xét:

+ Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

C = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}.

+ Tập hợp các kết quả có thể xảy ra đối với sự kiện “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4” là: D = {4; 8; 12} (gồm ba phần tử lấy ra từ tâp hợp C).

+ Trong trò chơi rút thẻ từ trong hộp, sự kiện “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4” cũng gọi là biến cố (hay gọi đầy đủ là biến cố ngẫu nhiên).

+ Mỗi kết quả: 4; 8; 12 (là phần tử của tập hợp D), được gọi là một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.

Ví dụ: Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ được rút ra là bình phương của một số tự nhiên”.

a) Viết tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Viết tập hợp H gồm các kết quả có thể xảy ra đối với biến cố trên.

c) Nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

C = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}.

b) Trong các số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12, các số là bình phương của một số tự nhiên là: 1; 4; 9 (vì 1² = 1; 2² = 4; 3² = 9).

Vậy sự kiện nói trên bao gồm những kết quả: 1; 4; 9 (gồm ba phần tử lấy ra từ tập hợp C = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}).

Tập hợp H gồm các kết quả có thể xảy ra đối với biến cố trên là: H = {1; 4; 9}.

c) Có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là bình phương của một số tự nhiên” là: 1; 4; 9 (lấy ra từ tập hợp C).

12. Xác suất của biến cố trong trò chơi gieo xúc xắc

Trong trò chơi gieo ngẫu nhiên xúc xắc một lần:

Xác suất của một biến cố trong trò chơi gieo xúc xắc bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.

Ví dụ: Gieo ngẫu nhiên xúc xắc một lần.

a) Tìm số phần tử của tập hợp E gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.

b) Xét biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3”. Tính xác suất của biến cố đó.

Hướng dẫn giải

a) Tập hợp gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:

E = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.

Vậy số phần tử của tập hợp E là 6.

b) Trong các số 1; 2; 3; 4; 5; 6, các số không chia hết cho 3 là: 1; 2; 4; 5.

Do đó có bốn kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3” là mặt 1 chấm; mặt 2 chấm; mặt 4 chấm; mặt 5 chấm.

Xác suất của biến cố đó là $\frac{4}{6}=\frac{2}{3}$.

Vậy xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3” là $\frac{2}{3}$.

Chú ý: Trong trò chơi gieo xúc xắc trên, số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là 6. Nếu k là số các kết quả thuận lợi cho biến cố thì xác suất của biến cố đó bằng .

Ví dụ: Gieo ngẫu nhiên xúc xắc một lần. Xét biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 2”.

a) Tìm k (số các kết quả thuận lợi cho biến cố trên).

b) Tính xác suất của biến cố đó.

Hướng dẫn giải

a) Trong các số 1; 2; 3; 4; 5; 6, ta có Ư(2) = {1; 2}.

Do đó có ba kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 2” là mặt 1 chấm, mặt 2 chấm.

Vậy k = 2.

b) Xác suất của biến cố đó là $\frac{k}{6}=\frac{2}{6}=\frac{1}{3}$.

Vậy xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 2” là $\frac{1}{3}$.

13. Xác suất của biến cố trong trò chơi rút thẻ từ trong hộp

Trong trò chơi rút thẻ từ trong hộp:

Xác suất của một biến cố trong trò chơi rút thẻ từ trong hộp bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

Ví dụ: Một hộp gồm 15 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; ...; 14; 15. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

a) Tìm số phần tử của tập hợp F gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Xét biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1”. Tính xác suất của biến cố đó.

Hướng dẫn giải

a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

F = {1; 2; 3; 4; ...; 14; 15}.

Vậy số phần tử của tập hợp F là 15.

b) Trong các số 1; 2; 3; 4; ...; 14; 15, các số chia 5 dư 1 là 1; 6; 11.

Do đó có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1” là 1; 6; 11.

Xác suất của biến cố đó là $\frac{3}{15}=\frac{1}{5}$.

Vậy xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1” là $\frac{1}{5}$.

Bài tập tổng hợp Toán 7 Chương 5

Bài 1. Cho các dãy dữ liệu sau:

+ Số điểm kiểm tra học kì I môn Toán của bạn An lần lượt là: 9,0; 7,5; 8,3; 5,8; 8,3; 9,0; 8,5.

+ Tên một số nhân vật trong phim hoạt hình Doraemon được bạn Minh ghi lại là: Doraemon, Nobita, Shizuka, Dorami, Suneo, Jaian, Dekisugi.

Trong hai loại dữ liệu thống kê trên, dữ liệu thống kê nào là số liệu? Dữ liệu thống kê nào không phải là số liệu?

Hướng dẫn giải

+ Số điểm kiểm tra học kì I môn Toán của bạn An là số liệu.

+ Tên một số nhân vật trong phim hoạt hình Doraemon không phải là số liệu.

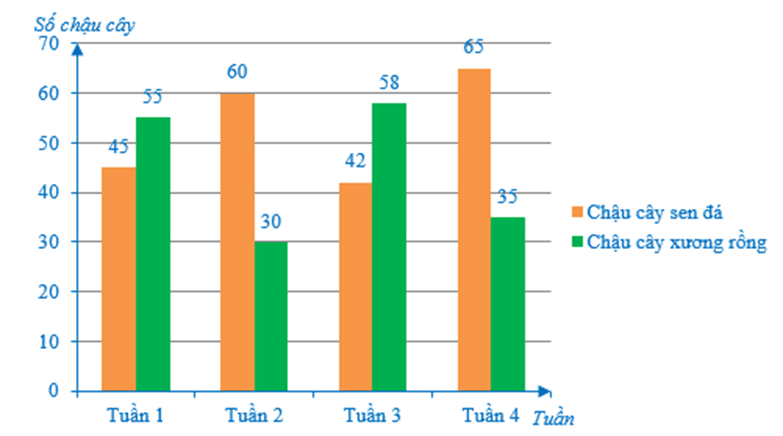
Bài 2. Nhà bạn Bình mở một cửa hàng bán cây cảnh, mỗi tuần nhập về 100 chậu cây (gồm một số lượng các chậu cây sen đá và một số lượng các chậu cây xương rồng). Bố bạn Bình có thể lựa chọn số lượng mỗi loại chậu cây, miễn là tổng số lượng của hai loại chậu đó bằng 100 chậu cây. Bạn Bình đã thống kê số lượng mỗi loại chậu cây mà cửa hàng nhập về trong một tháng và lập biểu đồ kép như hình bên:

Bạn Bình đã biểu diễn nhầm số liệu của một tuần trong biểu đồ cột kép trên. Theo em, bạn Bình đã biểu diễn nhầm số liệu của tuần nào?

Hướng dẫn giải

Ta tính tổng số chậu cây mỗi tuần cửa hàng nhà bạn Bình nhập về:

+ Tuần 1: 45 + 55 = 100 (chậu cây).

+ Tuần 2: 60 + 30 = 90 (chậu cây).

+ Tuần 3: 42 + 58 = 100 (chậu cây).

+ Tuần 4: 65 + 35 = 100 (chậu cây).

Theo đề, ta có mỗi tuần cửa hàng nhà bạn Bình nhập về 100 chậu cây.

Mà tổng số chậu cây ở tuần 2 chỉ có 90 chậu cây.

Vậy bạn Bình đã biểu diễn sai số liệu của tuần 2.

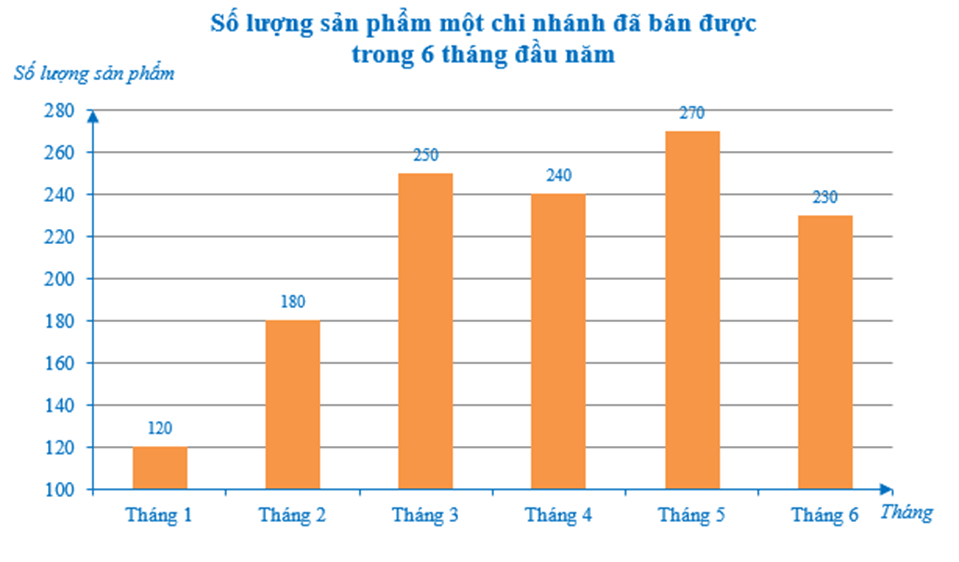
Bài 3. Biểu đồ dưới đây cho biết số lượng sản phẩm mà một chi nhánh đã bán được trong 6 tháng đầu năm:

a) Số lượng sản phẩm bán được ở tháng 3 tăng bao nhiêu phần trăm so với tháng 2 (làm tròn kết quả đến hàng phần mười)?

b) Số lượng sản phẩm bán được ở tháng 6 giảm bao nhiêu phần trăm so với tháng 5 (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải

a) Tỉ số phần trăm số lượng sản phẩm bán được ở tháng 3 và số lượng sản phẩm bán được ở tháng 2 là:

$\frac{250.100}{180}\%\approx \mathrm{138,9}\%$.

Vậy số lượng sản phẩm bán được ở tháng 3 tăng 138,9% – 100% = 38,9% so với tháng 2.

b) Tỉ số phần trăm số lượng sản phẩm bán được ở tháng 6 và số lượng sản phẩm bán được ở tháng 5 là:

$\frac{230.100}{270}\%\approx \mathrm{85,2}\%$.

Vậy số lượng sản phẩm bán được ở tháng 6 giảm 100% – 85,2% = 14,8% so với tháng 5.

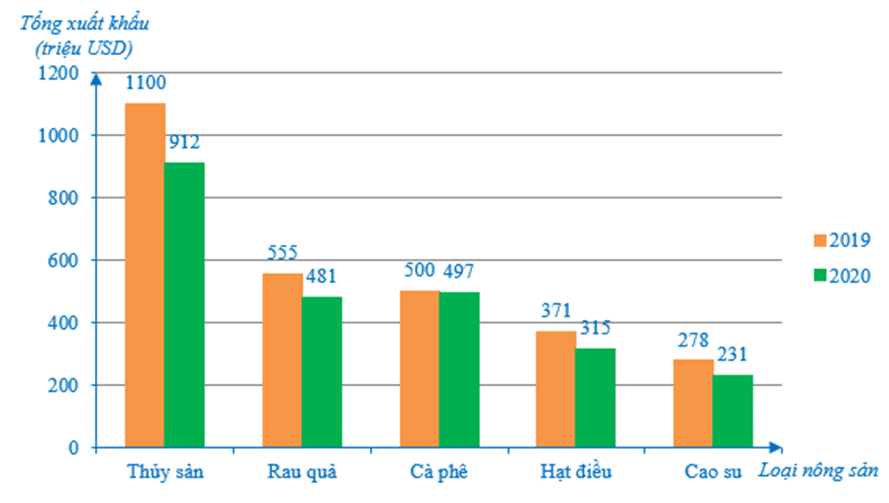
Bài 4. Biểu đồ sau đây cho biết tổng kim ngạch xuất khẩu nông sản 2 tháng đầu năm của Việt Nam giai đoạn 2019 – 2020:

(Theo thống kê của Tổng cục Hải quan)

a) Lập bảng thống kê tổng xuất khẩu nông sản 2 tháng đầu năm giai đoạn 2019 – 2020 theo mẫu sau:

Loại nông sản Tổng xuất khẩu của năm	Thủy sản	Rau quả	Cà phê	Hạt điều	Cao su
2019	?	?	?	?	?
2020	?	?	?	?	?

b) Loại nông sản nào Việt Nam có tổng xuất khẩu năm 2019 cao nhất? Loại nông sản nào Việt Nam có tổng xuất khẩu năm 2020 thấp nhất?

c) Bạn An kết luận rằng: Tổng xuất khẩu thủy sản của nước ta năm 2020 giảm 18,2% so với năm 2019. Theo em, kết luận của bạn An là đúng hay sai? Vì sao?

Hướng dẫn giải

a) Dựa vào biểu đồ ta có bảng sau:

Loại nông sản Tổng xuất khẩu của năm	Thủy sản	Rau quả	Cà phê	Hạt điều	Cao su
2019	1100	555	500	371	278
2020	912	481	497	315	231

b) Nhìn vào biểu đồ cột, ta thấy:

+ Ở năm 2019, thủy sản là loại nông sản có cột biểu diễn tổng xuất khẩu cao nhất.

+ Ở năm 2020, cao su là loại nông sản có cột biểu diễn tổng xuất khẩu thấp nhất.

Vậy năm 2019 Việt Nam có tổng xuất khẩu của thủy sản cao nhất; cao su có tổng xuất khẩu năm 2020 thấp nhất.

c) Tỉ số phần trăm giữa tổng xuất khẩu thủy sản năm 2020 và tổng xuất khẩu thủy sản năm 2019 là:

$\frac{912.100}{1100}\%\approx \mathrm{82,9}\%$.

Do đó tổng xuất khẩu thủy sản năm 2020 giảm 100% – 82,9% = 17,1% so với năm 2019.

Ta có 17,1% ≠ 18,2%.

Vậy bạn An đã kết luận sai.

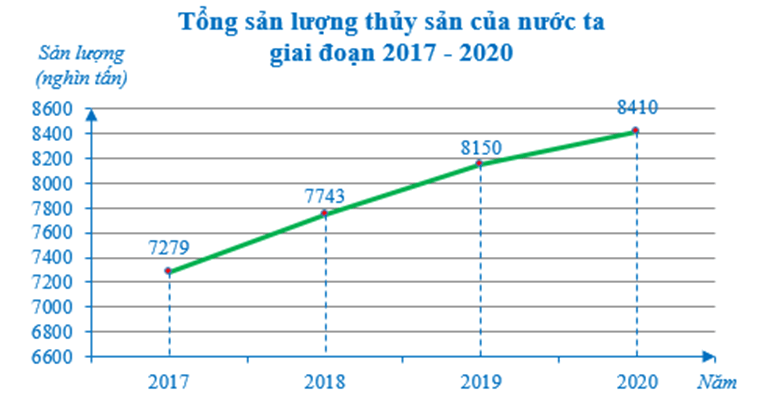
Bài 5. Tổng sản lượng thủy sản của nước ta giai đoạn 2017 – 2020 được thể hiện trong biểu đồ bên dưới:

a) Nêu tổng sản lượng thủy sản của nước ta trong những năm 2018 và 2020.

b) Dựa vào biểu đồ đoạn thẳng, nêu nhận xét về sản lượng thủy sản nuôi trồng của nước ta trong giai đoạn 2017 – 2020.

Hướng dẫn giải

a) Để xác định tổng sản lượng thủy sản của nước ta trong năm 2018, ta làm như sau:

+ Từ điểm “2018” trên trục nằm ngang, dóng theo chiều thẳng đứng tới đầu mút của đoạn thẳng thuộc đường gấp khúc;

+ Đi tiếp theo chiều ngang về bên trái cho đến khi gặp trục thẳng đứng;

+ Đọc chỉ số trên trục thẳng đứng.

Ta có: Tổng sản lượng thủy sản của nước ta trong năm 2018 là 7743 (nghìn tấn).

Tương tự như trên, tổng sản lượng thủy sản của nước ta trong năm 2020 là 8410 (nghìn tấn).

Vậy tổng sản lượng thủy sản của nước ta trong năm 2018 và năm 2020 lần lượt là 7743 và 8410 (nghìn tấn).

b) Dựa vào biểu đồ đoạn thẳng, ta thấy tổng sản lượng thủy sản của nước ta liên tục tăng trong giai đoạn 2017 – 2020.

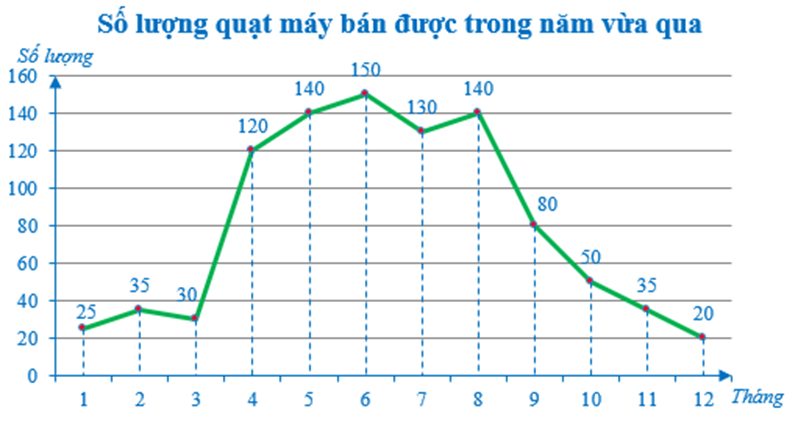
Bài 6. Biểu đồ sau đây cho biết số lượng quạt máy mà một cửa hàng đã bán được trong năm vừa qua:

a) Tính tổng số quạt máy bán được trong năm vừa qua.

b) Tìm ba tháng bán được nhiều quạt máy nhất? Tìm ba tháng bán được ít quạt máy nhất?

c) Bạn Cường kết luận rằng: Cửa hàng buôn bán tốt vào các tháng mùa hè. Em hãy cho biết bạn Cường kết luận đúng hay sai?

Hướng dẫn giải

a) Tổng số quạt máy bán được trong năm vừa qua là:

20 + 35 + 30 + 120 + 140 + 150 + 130 + 140 + 80 + 50 + 35 + 20 = 950 (quạt máy).

Vậy tổng số quạt máy cửa hàng bán được trong năm vừa qua là 950 quạt máy.

b) Quan sát biểu đồ đoạn thẳng, ta thấy:

+ Cửa hàng bán được nhiều quạt máy nhất vào các tháng 6; 5; 8 với số lượng quạt máy bán được lần lượt là 150; 140; 140 (quạt máy).

+ Cửa hàng bán được ít quạt máy nhất vào các tháng 12; 1; 3 với số lượng quạt máy bán được lần lượt là 20; 25; 30 (quạt máy).

c) Trong 3 tháng mùa hè (tháng 4; 5; 6), cửa hàng bán được số quạt máy lần lượt là 120; 140; 150.

Tổng số quạt máy cửa hàng bán được trong ba tháng này là:

120 + 140 + 150 = 410 (quạt máy).

Tổng số quạt máy cửa hàng bán được trong ba tháng cửa hàng bán đắt nhất (tháng 5; 6; 8) là:

150 + 140 + 140 = 430 (quạt máy).

Vì 410 ≈ 430 nên ta có:

Số lượng quạt máy cửa hàng bán được trong 3 tháng mùa hè xấp xỉ ba tháng cửa hàng bán đắt nhất.

Vậy bạn Cường đã kết luận đúng.

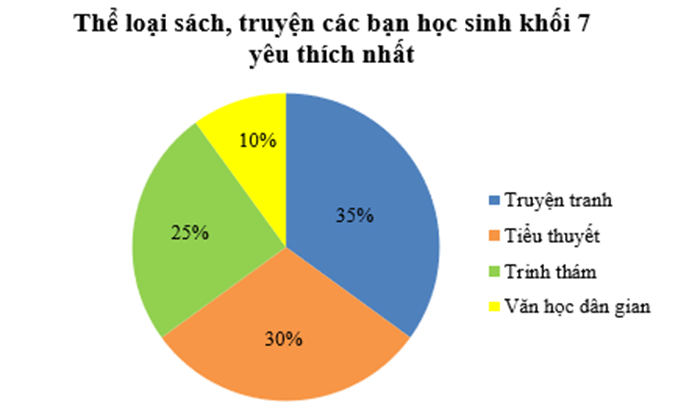
Bài 7. Biểu đồ dưới đây cho biết thể loại sách, truyện mà 200 bạn học sinh khối 7 yêu thích nhất:

a) Thể loại nào chiếm tỉ lệ cao nhất? Có bao nhiêu bạn yêu thích thể loại đó?

b) Thể loại nào chiếm tỉ lệ thấp nhất? Có bao nhiêu bạn yêu thích thể loại đó?

c) Số bạn thích truyện tranh nhiều hơn số bạn thích văn học dân gian bao nhiêu bạn?

Hướng dẫn giải

a) Thể loại truyện tranh chiếm tỉ lệ cao nhất với 35% so với cả bốn thể loại.

Số bạn yêu thích thể loại truyện tranh là: $\frac{200.35}{100}=70$ (bạn).

Vậy thể loại truyện tranh chiếm tỉ lệ cao nhất và có 70 bạn yêu thích thể loại truyện tranh.

b) Thể loại văn học dân gian chiếm tỉ lệ thấp nhất với 10% so với cả bốn thể loại.

Số bạn yêu thích thể loại văn học dân gian là: $\frac{200.10}{100}=20$ (bạn).

Vậy thể loại văn học dân gian chiếm tỉ lệ thấp nhất và có 20 bạn yêu thích thể loại văn học dân gian.

c) Số bạn thích truyện tranh nhiều hơn số bạn thích văn học dân gian là: 70 – 20 = 50 (bạn).

Vậy số bạn thích truyện tranh nhiều hơn số bạn thích văn học dân gian là 50 bạn.

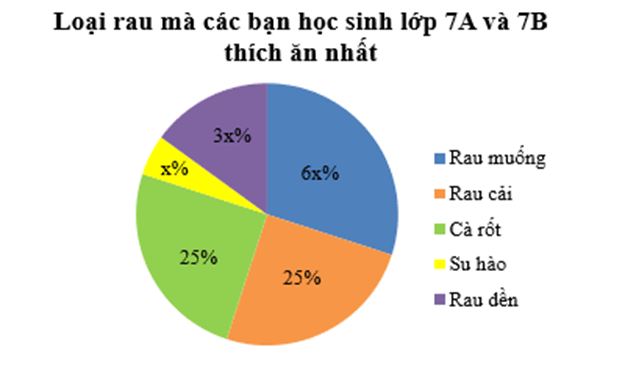
Bài 8. Biểu đồ sau thể hiện loại rau mà các bạn học sinh lớp 7A và 7B thích ăn nhất trong năm loại: rau muống, rau cải, cà rốt, su hào, rau dền.

a) Tìm giá trị của x.

b) Tính tỉ số phần trăm số học sinh thích ăn rau muống, su hào, rau dền so với tổng số học sinh.

c) Tính và so sánh số học sinh thích ăn rau cải và số học sinh thích ăn cà rốt.

Hướng dẫn giải

a) Ta có 6x% + 25% + 25% + x% + 3x% = 100%.

Suy ra 10x% + 50% = 100%.

Do đó 10x% = 50%.

Khi đó x% = 50% : 10 = 5%.

Vậy x = 5.

b) Tỉ số phần trăm số học sinh thích ăn rau muống nhất là: 6.5% = 30%.

Tỉ số phần trăm số học sinh thích ăn su hào nhất là: 5%.

Tỉ số phần trăm số học sinh thích ăn rau dền nhất là: 3.5% = 15%.

Vậy tỉ số phần trăm số học sinh thích ăn rau muống, su hào, rau dền so với tổng số học sinh lần lượt là 30%, 5%, 15%.

c) Quan sát biểu đồ, ta thấy số học sinh thích ăn rau cải và số học sinh thích ăn cà rốt đều bằng 25%.

Vậy số học sinh thích ăn rau cải và số học sinh thích ăn cà rốt bằng nhau.

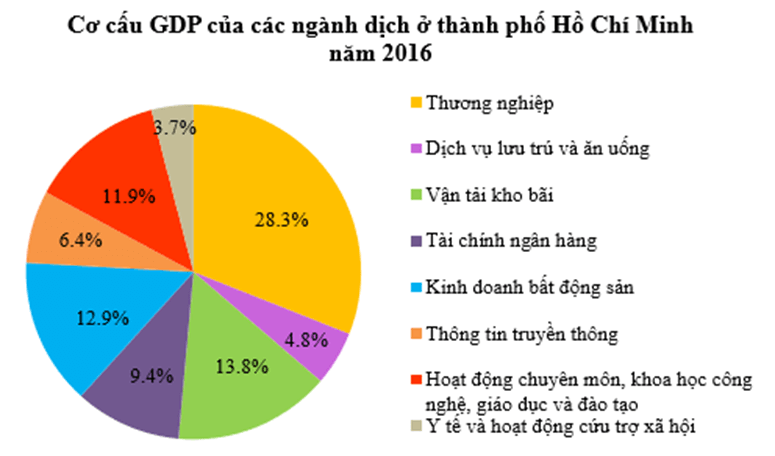
Bài 9. Biểu đồ sau đây thể hiện cơ cấu GDP của các ngành dịch vụ ở thành phố Hồ Chí Minh năm 2016 (đơn vị: %):

a) Trong dịch vụ tiêu dùng (Thương nghiệp; Dịch vụ lưu trú và ăn uống), ngành dịch vụ nào chiếm tỉ lệ cao nhất?

b) Tổng tỉ lệ dịch vụ sản xuất (Vận tải kho bãi; Tài chính ngân hàng; Kinh doanh bất động sản) gấp khoảng bao nhiêu lần so với tổng tỉ lệ dịch vụ công cộng (Thông tin truyền thông; Hoạt động chuyên môn, khoa học công nghệ, giáo dục và đào tạo; Y tế và hoạt động cứu trợ xã hội) (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải

a) Quan sát biểu đồ, ta có 28,3% > 4,8%.

Vậy trong dịch vụ tiêu dùng, ngành dịch vụ chiếm tỉ lệ cao nhất là Thương nghiệp.

b) Tổng tỉ lệ dịch vụ sản xuất là: 13,8% + 9,4% + 12,9% = 36,1%.

Tổng tỉ lệ dịch vụ công cộng là: 6,4% + 11,9% + 3,7% = 22%.

Tổng tỉ lệ dịch vụ sản xuất gấp số lần so với tổng tỉ lệ dịch vụ công cộng là khoảng:

36,1% : 22% ≈ 1,6.

Vậy tổng tỉ lệ dịch vụ sản xuất gấp khoảng 1,6 lần so với tổng tỉ lệ dịch vụ công cộng.

Bài 10. Một hộp gồm có 30 chiếc thẻ, mỗi chiếc thẻ được ghi một trong các số 1; 2; 3; 4; 5; 6; ...; 29; 30. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

a) Viết tập hợp X gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Xét biến cố “Số xuất hiện trên thẻ được rút ra là bội của 5”. Viết tập hợp Y gồm các kết quả có thể xảy ra và nêu những kết quả thuận lợi cho biến cố đó.

c) Xét biến cố “Số xuất hiện trên thẻ được rút ra là ước chung của 24 và 28”. Viết tập hợp Z gồm các kết quả có thể xảy ra và nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

X = {1; 2; 3; 4; 5; 6; ...; 29; 30}.

b) Ta có B(5) = {5; 10; 15; 20; 25; 30}.

Vậy tập hợp Y gồm các kết quả xảy ra đối với biến cố trên là:

Y = {5; 10; 15; 20; 25; 30} (lấy ra từ tập hợp X).

Có sáu kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là bội của 5” là: 5; 10; 15; 20; 25; 30 (lấy ra từ tập hợp X).

c) Ta có:

+) Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.

+) Ư(28) = {1; 2; 4; 7; 14; 28}.

Do đó ƯC(24; 28) = {1; 2; 4}.

Vậy tập hợp Z gồm các kết quả xảy ra đối với biến cố trên là:

Z = {1; 2; 4} (lấy ra từ tập hợp X).

Có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là ước chung của 24 và 28” là: 1; 2; 4 (lấy ra từ tập hợp X).

Bài 11. Trên giá sách có 10 quyển sách khác nhau: Doraemon, Conan, Cổ tích, Ngữ văn, Toán, Lịch sử, Khoa học tự nhiên, Tiếng Anh, Từ điển Anh – Việt, Từ điển Pháp – Việt. Chọn ngẫu nhiên một quyển sách trên giá sách.

a) Xét biến cố “Quyển sách được chọn là truyện tranh”. Nêu những kết quả thuận lợi cho biến cố đó.

b) Xét biến cố “Quyển sách được chọn là sách liên quan đến ngoại ngữ”. Nêu những kết quả thuận lợi cho biến cố đó.

c) Xét biến cố “Quyển sách được chọn là sách giáo khoa và liên quan đến văn học dân gian”. Nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Thể loại truyện tranh gồm có các quyển: Doraemon, Conan.

Vậy có hai kết quả thuận lợi cho biến cố “Quyển sách được chọn là truyện tranh” là Doraemon và Conan.

b) Các sách liên quan đến ngoại ngữ là: Tiếng Anh, Từ điển Anh – Việt, Từ điển Pháp – Việt.

Vậy có ba kết quả thuận lợi cho biến cố “Quyển sách được chọn là sách liên quan đến ngoại ngữ” là Tiếng Anh, Từ điển Anh – Việt, Từ điển Pháp – Việt.

c) Thể loại sách giáo khoa gồm có các quyển: Ngữ văn, Toán, Lịch sử, Khoa học tự nhiên, Tiếng Anh.

Quyển sách liên quan đến văn học dân gian là: Cổ tích.

Vậy có sáu kết quả thuận lợi cho biến cố “Quyển sách được chọn là sách giáo khoa và liên quan đến văn học dân gian” là Ngữ văn, Toán, Lịch sử, Khoa học tự nhiên, Tiếng Anh, Cổ tích.

Bài 12. Một hộp chứa 20 viên bi gồm 8 viên bi đỏ, 5 viên bi vàng và 7 viên bi xanh. Mỗi viên bi đỏ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8, mỗi viên bi vàng được ghi một trong các số 9; 10; 11; 12; 13, mỗi viên bi xanh được ghi một trong các số 14; 15; 16; 17; 18; 19; 20. Hai viên bi khác nhau được ghi hai số khác nhau. Lấy ra ngẫu nhiên một viên bi trong hộp đó.

a) Viết tập hợp D gồm các kết quả có thể xảy ra đối với viên bi được lấy ra.

b) Xét biến cố “Viên bi được lấy ra có màu vàng”. Nêu những kết quả thuận lợi cho biến cố đó.

c) Xét biến cố “Viên bi được lấy ra có màu đỏ hoặc xanh”. Nêu những kết quả thuận lợi cho biến cố đó.

d) Xét biến cố “Viên bi được lấy ra có màu đỏ hoặc vàng và số ghi trên viên bi là một số chia hết cho 2”. Nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Tập hợp D gồm các kết quả có thể xảy ra đối với viên bi được lấy ra là:

D = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20}.

b) Trong 20 viên bi, viên bi có màu vàng được ghi một trong các số 9; 10; 11; 12; 13.

Vậy có năm kết quả thuận lợi cho biến cố “Viên bi được lấy ra có màu vàng” là: 9; 10; 11; 12; 13.

c) Trong 20 viên bi, ta có:

+) Viên bi có màu đỏ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8.

+) Viên bi có màu xanh được ghi một trong các số 14; 15; 16; 17; 18; 19; 20.

Vậy có 15 kết quả thuận lợi cho biến cố “Viên bi được lấy ra có màu đỏ hoặc xanh” là: 1; 2; 3; 4; 5; 6; 7; 8; 14; 15; 16; 17; 18; 19; 20.

d) Ta có:

+) Viên bi có màu đỏ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8.

+) Viên bi có màu vàng được ghi một trong các số 9; 10; 11; 12; 13.

+) Các số chia hết cho 2 trong các số trên là: 2; 4; 6; 8; 10; 12.

Vậy có sáu kết quả thuận lợi cho biến cố “Viên bi được lấy ra có màu đỏ hoặc vàng và số ghi trên viên bi là một số chia hết cho 2” là: 2; 4; 6; 8; 10; 12.

Bài 13. Một hộp có 40 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; ...; 39; 40. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

a) Tìm số phần tử của tập hợp H gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Tính xác suất của biến cố “Số trên thẻ được rút ra là số có chữ số tận cùng là 7”.

c) Tính xác suất của biến cố “Số trên thẻ được rút ra là số chia hết cho cả 2 và 3”.

Hướng dẫn giải

a) Tập hợp gồm các kết quả có thể xảy ra đối với số trên thẻ được rút ra là:

H = {1; 2; 3; 4; ...; 39; 40}.

Vậy số phần tử của tập hợp H là 40.

b) Trong các số 1; 2; 3; 4; ...; 39; 40, các số có chữ số tận cùng là 7 là: 7; 17; 27; 37.

Do đó có bốn kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra là số có chữ số tận cùng là 7” là 7; 17; 27; 37.

Xác suất của biến cố đó là: $\frac{4}{40}=\frac{1}{10}$.

Vậy xác suất của biến cố “Số trên thẻ được rút ra là số có chữ số tận cùng là 7” là $\frac{1}{10}$.

c) Trong các số 1; 2; 3; ...; 39; 40, các số chia hết cho 2 là: 2; 4; 6; 8; 10; 12; 14; 16; ...; 38; 40.

Trong các số 1; 2; 3; ...; 39; 40, các số chia hết cho 3 là: 3; 6; 9; 12; 15; 18; ...; 33; 36; 39.

Do đó trong các số được nêu ở trên, các số chia hết cho cả 2 và 3 là 6; 12; 18; 24; 30; 36.

Khi đó ta có sáu kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra là số chia hết cho cả 2 và 3” là 6; 12; 18; 24; 30; 36.

Xác suất của biến cố đó là: $\frac{6}{40}=\frac{3}{20}$.

Vậy xác suất của biến cố “Số trên thẻ được rút ra là số chia hết cho cả 2 và 3” là $\frac{3}{20}$.

Bài 14. Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Nhà giáo Việt Nam 20/11, bạn lớp trưởng đã chọn ra 10 bạn tập múa gồm các bạn: Hoa, Thảo, Mai, Dũng, Cường, Bình, Châu, Minh, My, Phúc. Chọn ngẫu nhiên một bạn trong nhóm 10 bạn tập múa trên.

a) Tìm số phần tử của tập hợp P gồm các kết quả xảy ra đối với tên học sinh được chọn ra.

b) Tính xác suất của biến cố “Học sinh được chọn ra có tên bắt đầu bằng chữ M”.

Hướng dẫn giải

a) Tập hợp gồm các kết quả xảy ra đối với tên học sinh được chọn ra là:

P = {Hoa, Thảo, Mai, Dũng, Cường, Bình, Châu, Minh, My, Phúc}.

Vậy tập hợp P gồm có 10 phần tử.

b) Trong số các bạn Hoa, Thảo, Mai, Dũng, Cường, Bình, Châu, Minh, My, Phúc, các bạn có tên bắt đầu bằng chữ M là: Mai, Minh, My.

Do đó có ba kết quả thuận lợi cho biến cố “Học sinh được chọn ra có tên bắt đầu bằng chữ M” là Mai, Minh, My.

Xác suất của biến cố đó là $\frac{3}{10}$.

Vậy xác suất của biến cố “Học sinh được chọn ra có tên bắt đầu bằng chữ M” là $\frac{3}{10}$.

Bài 15. Bạn Cường vào cửa hàng KFC và dự định chọn một suất gà rán. Khi đọc menu, bạn Cường thấy cửa hàng đang có các món như sau: combo gà rán (ưu đãi) có giá 97 000 đồng, combo gà viên (ưu đãi) có giá 84 000 đồng, gà rán – 1 miếng có giá 35 000 đồng, gà rán – 2 miếng có giá 68 000 đồng, gà rán – 3 miếng có giá 101 000 đồng, cánh gà rán hot wings – 3 miếng có giá 48 000 đồng. Bạn Cường cảm thấy món nào cũng ngon hết nên dự định nhắm mắt chỉ tay ngẫu nhiên vào một món.

a) Tìm số phần tử của tập hợp G gồm các kết quả có thể xảy ra đối với món gà được bạn Cường chọn.

b) Tính xác suất của biến cố “Món gà được bạn Cường chọn có giá dưới 70 000 đồng”.

c) Tính xác suất của biến cố “Món gà được bạn Cường chọn có giá trên 90 000 đồng”.

d) Tính xác suất của biến cố “Bạn Cường chọn được các combo ưu đãi”.

e) Tính xác suất của biến cố “Bạn Cường chọn được các món không phải là combo ưu đãi và có giá trên 100 000 đồng”.

Hướng dẫn giải

a) Tập hợp gồm các kết quả có thể xảy ra đối với món gà được bạn Cường chọn là:

G = {combo gà rán, combo gà viên, gà rán – 1 miếng, gà rán – 2 miếng, gà rán – 3 miếng, cánh gà rán hot wings – 3 miếng}.

Vậy số phần tử của tập hợp G là 6 phần tử.

b) Trong các món gà, các món có giá dưới 70 000 đồng là: gà rán – 1 miếng có giá 35 000 đồng, gà rán – 2 miếng có giá 68 000 đồng, cánh gà rán hot wings – 3 miếng có giá 48 000 đồng.

Do đó có ba kết quả thuận lợi cho biến cố “Món gà được bạn Cường chọn có giá dưới 70 000 đồng” là gà rán – 1 miếng, gà rán – 2 miếng, cánh gà hot wings – 3 miếng.

Xác suất của biến cố đó là $\frac{3}{6}=\frac{1}{2}$.

Vậy xác suất của biến cố “Món gà được bạn Cường chọn có giá dưới 70 000 đồng” là $\frac{1}{2}$.

c) Trong các món gà, các món có giá trên 90 000 đồng là: combo gà rán có giá 97 000 đồng, gà rán – 3 miếng có giá 101 000 đồng.

Do đó có hai kết quả thuận lợi cho biến cố “Món gà được bạn Cường chọn có giá trên 90 000 đồng” là combo gà rán, gà rán – 3 miếng.

Xác suất của biến cố đó là $\frac{2}{6}=\frac{1}{3}$.

Vậy xác suất của biến cố “Món gà được bạn Cường chọn có giá trên 90 000 đồng” là $\frac{1}{3}$.

d) Trong các món gà, các món combo ưu đãi gồm có: combo gà rán, combo gà viên.

Do đó có hai kết quả thuận lợi cho biến cố “Bạn Cường chọn được các combo ưu đãi” là combo gà rán, combo gà viên.

Xác suất của biến cố đó là $\frac{2}{6}=\frac{1}{3}$.

Vậy xác suất của biến cố “Bạn Cường chọn được các combo ưu đãi” là $\frac{1}{3}$.

e) Trong các món gà, các món không phải combo ưu đãi là: gà rán – 1 miếng, gà rán – 2 miếng, gà rán – 3 miếng, cánh gà rán hot wings – 3 miếng.

Trong các món kể trên, các món có giá trên 100 000 đồng là gà rán – 3 miếng.

Do đó có một kết quả thuận lợi cho biến cố “Bạn Cường chọn được các món không phải là combo và có giá trên 100 000 đồng” là gà rán – 3 miếng.

Xác suất của biến cố đó là $\frac{1}{6}$.

Vậy xác suất của biến cố “Bạn Cường chọn được các món không phải là combo ưu đãi và có giá trên 100 000 đồng” là $\frac{1}{6}$.

Học tốt Toán 7 Chương 5

Các bài học để học tốt Chương 5 Toán lớp 7 hay khác:

• Giải sgk Toán 7 Bài tập cuối chương 5

• Giải sbt Toán 7 Bài tập cuối chương 5

Xem thêm tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:

• Lý thuyết Toán 7 Bài 1: Biểu thức số. Biểu thức đại số

• Lý thuyết Toán 7 Bài 2: Đa thức một biến. Nghiệm của đa thức một biến

• Lý thuyết Toán 7 Bài 3: Phép cộng, phép trừ đa thức một biến

• Lý thuyết Toán 7 Bài 4: Phép nhân đa thức một biến

• Lý thuyết Toán 7 Bài 5: Phép chia đa thức một biến

Xem thêm các tài liệu học tốt lớp 7 hay khác:

• Giải sgk Toán 7 Cánh diều
• Giải SBT Toán 7 Cánh diều
• Giải lớp 7 Cánh diều (các môn học)
• Giải lớp 7 Kết nối tri thức (các môn học)
• Giải lớp 7 Chân trời sáng tạo (các môn học)

---