Bài tập Ôn hè Toán 6 lên 7 (có lời giải)
Tài liệu bài tập ôn hè Toán lớp 6 lên 7 đầy đủ cả năm với bài tập đa dạng có lời giải chi tiết giúp học sinh lớp 6 nắm vững kiến thức trọng tâm Toán 6.
Bài tập Ôn hè Toán 6 lên 7 (có lời giải)
CHỦ ĐỀ 1. TẬP HỢP CÁC SỐ TỰ NHIÊN, SỐ NGUYÊN
I. LÝ THUYẾT
1. Tập hợp
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Kí hiệu:
• x ∈ A đọc là x thuộc A hoặc x nằm trong A.
• y ∉ A đọc là y không thuộc A.
2. Cách viết (mô tả) một tập hợp
Ta thường viết tập hợp theo 2 cách:
Cách 1. Liệt kê các phần tử của tập hợp
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “;”.
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
3. Tập hợp số tự nhiên, số nguyên
• Tập hợp không có phần tử nào gọi là tập hợp rỗng. Kí hiệu: ∅.
• Tập hợp các số tự nhiên được kí hiệu là ℕ, ℕ = {0;1;2;3;....}.
• Tập hợp các số tự nhiên khác 0 được kí hiệu là ℕ*, ℕ* = {1;2;3;....}.
• Tập hợp các số nguyên được kí hiệu là ℤ, ℤ = .
Số nguyên dương là tập hợp các số nguyên lớn hơn 0;
Số nguyên âm là tập hợp các số nguyên nhỏ hơn 0.
Số 0 không là số nguyên dương, cũng không là số nguyên âm.
4. Tập hợp con
• Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A được gọi là tập hợp con của tập hợp B. Kí hiệu: A ⊂ B.
• Nếu A ⊂ B và B ⊂ A thì hai tập hợp A và B bằng nhau. Kí hiệu A = B.
5. Biểu diễn số nguyên trên trục số
Mỗi số nguyên âm được biểu diễn bởi một điểm ở bên trái điểm 0 (chẳng hạn điểm a) và mỗi số tự nhiên (số nguyên dương) được biểu diễn bởi một điểm ở trên phải điểm 0 (chẳng hạn điểm b).
Khi đó a < b.
6. Số đối
Số đối của số nguyên a là số -a.
II. MỘT SỐ DẠNG BÀI TẬP
Dạng 1. Biểu diễn một tập hợp cho trước
Dạng 2. Quan hệ giữa phần tử và tập hợp, giữa tập hợp và tập hợp
Dạng 3. Xác định số phần tử của một tập hợp
Dạng 4. Tập hợp con
Dạng 5. Biểu diễn số nguyên trên trục số
Dạng 6. Số đối
III. BÀI TẬP
Bài 1. Viết tập hợp A và B các chữ cái trong các cụm từ “GIÁO VIÊN”, “HỌC SINH”.
Bài 2. Viết tập hợp sau bằng cách liệt kê các phần tử
a) A = {x ∈ ℕ | 10 < x < 16};
b) B = {x ∈ ℤ | -2 ≤ x < 3}.
Bài 3. Viết tập hợp sau bằng cách chỉ ra tính chất đặc trưng:
a) A = {2;4;6;8;10};
b) B = {0;5;10;15;20;25;30}.
Bài 4. Viết tập hợp các số tự nhiên lẻ lớn hơn 7 và nhỏ hơn hoặc bằng 17 bằng hai cách.
Bài 5.
a) Cho tập hợp A = {3;-5;7}. Hãy điền kí hiệu ∈; ∉; ⊂; = thích hợp vào ô trống:
b) Điền kí hiệu (∈; ∉; ∩; ⊂)vào ô trống:
Bài 6. Gọi A là tập hợp các số nguyên lẻ có 3 chữ số. Hỏi tập hợp A có bao nhiêu phần tử? Tính tổng giá trị tất cả các phần tử của tập hợp A.
Bài 7. Cho tập hợp A = {a;b;c;d}
a) Viết các tập hợp con của A có một phần tử.
b) Viết các tập hợp con của A có hai phần tử.
c) Có bao nhiêu tập hợp con của A có ba phần tử? có bốn phần tử?
d) Tập hợp A có bao nhiêu tập hợp con?
Bài 8. Cho các tập hợp A = {-2;-3;5;7;11} và B = {1;-3;5;7;-9;11}
a) Viết tập hợp C các phần tử thuộc A và không thuộc B.
b) Viết tập hợp D các phần tử thuộc B và không thuộc A.
c) Viết tập hợp E các phần tử vừa thuộc A vừa thuộc B.
d) Viết tập hợp F các phần tử hoặc thuộc A hoặc thuộc B.
Bài 9. Cho trục số như hình vẽ dưới.
Các điểm A,B,C biểu diễn những số nguyên nào? Tìm số đối của các số nguyên đó.
IV. ĐÁP ÁN BÀI TẬP
Bài 1.
Tập hợp các chữ cái trong cụm từ “GIÁO VIÊN” là: A = {G; I; A; O; V; Ê; N}.
Tập hợp các chữ cái trong cụm từ “HỌC SINH” là: B = {H; O; C; S; I; N}.
Bài 2.
a) A = {11;12;13;14;15};
b) B = {-2;-1;0;1;2}.
Bài 3.
a) A là tập hợp các số chẵn khác 0 và nhỏ hơn 10 (hoặc A là tập hợp các số chẵn khác 0 và có một chữ số).
c) B là tập hợp các số chia hết cho 5 và không vượt quá 30.
Bài 4.
Cách 1: A = {9;11;;13;15;17}.
Cách 2: A = {7 < x ≤ 17 | x là số lẻ}.
Bài 5.
Bài 6.
Tập hợp các số nguyên lẻ có 3 chữ số là
A = {-999;-997;...;-103;-101;101;103;...;997;999}.
Tập hợp A có phần tử.
Tổng của tất cả các phần tử là:
= 0.
Bài 7.
a) Các tập hợp con của A có một phần tử: .
b) Các tập hợp con của A có hai phần tử: .
c) Các tập hợp con của A có ba phần tử: .
Các tập hợp con của A có bốn phần tử: .
d) Tập hợp A có 24 = 16 tập hợp con.
Bài 8.
a) Tập hợp C các phần tử thuộc A và không thuộc B là C = {-2}.
b) Tập hợp D các phần tử thuộc B và không thuộc A là D = {1;9}.
c) Tập hợp E các phần tử vừa thuộc A vừa thuộc B là E = {-3;5;7;11}.
d) Tập hợp F các phần tử hoặc thuộc A hoặc thuộc B là F = {1;-2;-3;5;7;-9;11}.
Bài 9. Cho trục số như hình vẽ dưới.
Các điểm A,B,C lần lượt biểu diễn những số nguyên -6;-2;3.
Số đối của -6 là 6; Số đối của -2 là 2; Số đối của 3 là -3.
................................
................................
................................
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 6 (các môn học)
- Giáo án điện tử lớp 6 (các môn học)
- Giáo án Ngữ văn 6
- Giáo án Toán 6
- Giáo án Tiếng Anh 6
- Giáo án Khoa học tự nhiên 6
- Giáo án Lịch Sử 6
- Giáo án Địa Lí 6
- Giáo án GDCD 6
- Giáo án Tin học 6
- Giáo án Công nghệ 6
- Giáo án HĐTN 6
- Giáo án Âm nhạc 6
- Giáo án Vật Lí 6
- Giáo án Sinh học 6
- Đề thi lớp 6 (các môn học)
- Đề thi Toán 6 (có đáp án)
- Đề cương ôn tập Toán lớp 6
- Chuyên đề dạy thêm Toán 6 năm 2024 (có lời giải)
- Đề thi Ngữ Văn 6 (có đáp án)
- Chuyên đề Tiếng Việt lớp 6
- Bộ Đề thi Tiếng Anh 6 (có đáp án)
- Bộ Đề thi Khoa học tự nhiên 6 (có đáp án)
- Đề thi Lịch Sử & Địa Lí 6 (có đáp án)
- Đề thi Địa Lí 6 (có đáp án)
- Đề thi Lịch Sử 6 (có đáp án)
- Đề thi GDCD 6 (có đáp án)
- Đề thi Tin học 6 (có đáp án)
- Đề thi Công nghệ 6 (có đáp án)
- Đề thi Toán Kangaroo cấp độ 3 (Lớp 5, 6)

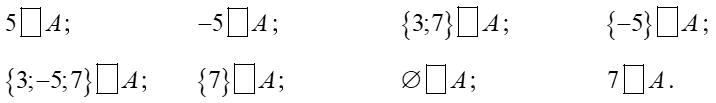

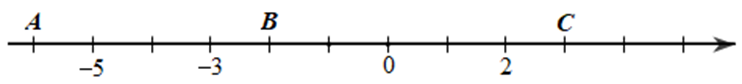



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

