10 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2024 (có đáp án)

Với bộ 15 Đề thi Giữa kì 1 Toán 6 năm 2024 có đáp án, chọn lọc được biên soạn bám sát nội dung sách Kết nối tri thức và sưu tầm từ đề thi Toán 6 của các trường THCS trên cả nước. Hi vọng bộ đề thi này sẽ giúp học sinh ôn tập và đạt kết quả cao trong các bài thi Giữa học kì 1 Toán 6.

10 Đề thi Giữa kì 1 Toán 6 Kết nối tri thức năm 2024 (có đáp án)

Xem thử

Chỉ từ 150k mua trọn bộ Đề thi Giữa kì 1 Toán 6 Kết nối tri thức bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2024 - 2025

Bài thi môn: Toán 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 1)

I. Trắc nghiệm (2 điểm)

Câu 1. Cho tập hợp A = {chó, mèo, lợn, gà}. Phát biểu nào dưới đây là đúng?

A. Chó ∈ A;

B. Mèo ∉ A;

C. Cá ∈ A;

D. Lợn ∉ A.

Câu 2. Chữ số 2 trong số 123 857 có giá trị là:

A. 120 000

B. 20 000

C. 23 857

D. 20

Câu 3. Trong các số sau: 114, 76; 1 029; 354; 57. Có bao nhiêu số chia hết cho 3?

A. 3

B. 0

C. 5

D. 4

Câu 4. Kết quả của phép tính sau: 7⁸ : 7

A. 7⁸;

B. 7⁶;

C. 7⁷;

D. 7⁹.

II. Tự luận (8 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 12 + 3.2⁵ : 4 – 3;

b) 120 + [55 – (11 – 3.2)²] + 2³;

c) 24⁰.14.83 + 7.2.17.

Bài 2. (2 điểm) Tìm x, biết:

a) 2x + 15 = 242:2;

b) (3x – 4)³ = 125;

c) x ∈ ƯC(18,54) và x > 6.

Bài 3. (1 điểm) Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2 và 5, lớn hơn 12 nhỏ hơn hoặc bằng 70. Hãy viết tập hợp A theo hai cách.

Bài 4. (1,5 điểm) Tuấn và Hà mỗi người mua một số hộp bút chì màu, trong mỗi hộp đều có từ hai chiếc bút trở lên và số bút trong mỗi hộp là như nhau. Tính ra Tuấn mua 25 bút, Hà mua 20 bút. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc?

Bài 5. (0,5 điểm) Tìm số tự nhiên có hai chữ số biết số đó chia cho tổng các chữ số của nó thu được 7 dư 6.

Đáp án & Hướng dẫn giải

I. Trắc nghiệm (2 điểm)

Câu 1.

Ta có:

Chó là một phần tử của tập hợp A nên ta viết chó ∈ A. Do đó A đúng.

Mèo là một phần tử của tập hợp A nên ta viết mèo ∈ A. Do đó B sai.

Cá không phải là phần tử của tập hợp A nên ta viết cá ∉ A. Do đó C sai.

Lợn là một phần tử của tập hợp A nên ta viết lợn ∈ A. Do đó D sai.

Chọn A.

Câu 2.

Trong số 123 857, chữ số 2 là chữ số hàng chục nghìn nên chữ số 2 có giá trị 2.10 000 = 20 000.

Chọn B.

Câu 3.

Ta có:

1 + 1 + 4 = 6 chia hết cho 3 nên 114 chia hết cho 3;

7 + 6 = 13 không chia hết cho 3 nên 76 không chia hết cho 3;

1 + 0 + 2 + 9 = 12 chia hết cho 3 nên 1 029 chia hết cho 3;

3 + 5 + 4 = 12 chia hết cho 3 nên 354 chia hết cho 3;

5 + 7 = 12 chia hết cho 3 nên 57 chia hết cho 3.

Vậy có 4 số chia hết cho 3.

Chọn D

Câu 4.

Ta có: 7⁸ : 7 = 7^{8 – 1} = 7⁷.

Chọn C.

II. Tự luận (8 điểm)

Bài 1.

a) 12 + 3.2⁵ : 4 – 3

= 12 + 3.32:4 – 3

= 12 + 3.8 – 4

= 12 + 24 – 4

= 36 – 4

= 32

b) 120 + [55 – (11 – 3.2)²] + 2³

= 120 + [55 – (11 – 6)²] + 8

= 120 + [55 – 4²] + 8

= 120 + [55 – 16] + 8

= 120 + 39 + 8

= 159 + 8

= 167

c) 24⁰.14.83 + 7.2.17

= 14.83 + 14.17

= 14.(83 + 17)

= 14.100

= 1 400.

Bài 2.

a) 2x + 15 = 242:2

2x + 15 = 121

2x = 121 – 15

2x = 106

x = 106 : 2

x = 53.

Vậy x = 53.

b) (3x – 4)³ = 125

(3x – 4)³ = 5³

3x – 4 = 5

3x = 5 + 4

3x = 9

x = 9:3

x = 3.

Vậy x = 3.

c) x ƯC(18,54) và x > 6

Ta có: 18 = 2.3², 54 = 2.3³

Khi đó: ƯCLN(18, 54) = 2.3² = 18.

ƯC(18,54) = Ư(18) = {1; 2; 3; 6; 9; 18}

x ∈ {1; 2; 3; 6; 9; 18}

Mà x > 6 nên x ∈ {9; 18}.

Vậy x ∈ {9; 18}.

Bài 3.

Các số tự nhiên chia hết cho 2 và cho 5 là các số tự nhiên có chữ số tận cùng bằng 0: 0; 10; 20; 30; 40; 50; 60; 70; 80; …

Các số tự nhiên ở trên thỏa mãn lớn hơn 12 nhỏ hơn hoặc bằng 70 là: 20; 30; 40; 50; 60; 70.

Theo cách liệt kê, tập hợp A được mô tả: A = {20; 30; 40; 50; 60; 70}.

Theo cách chỉ ra tính chất đặc trưng, ta viết: {x ∈ N|x2, x5, 12 < x ≤ 70}

Bài 4.

Gọi số bút trong mỗi hộp bút chì màu là x ( x ∈ N, x > 2) (chiếc).

Vì số bút trong mỗi hộp là như nhau nên 25 và 20 chia hết cho x hay x ƯC(25, 20).

Ta có: 25 = 5², 20 = 2².5;

ƯCLN(25, 20) = 5.

ƯC(25, 20) = Ư(5) = {1; 5}

x ∈ {1; 5}

Mà x > 2 nên x = 5 (thỏa mãn điều kiện).

Vậy trong mỗi hộp có 5 chiếc bút.

Bài 5.

Gọi số tự nhiên có hai chữ số cần tìm là 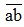 (Với a,b {0;1;2;3; …; 9} và a ≠ 0 )

Ta có tổng các chữ số của nó là: a + b.

Vì số dư phép chia là 6 nên a + b > 6.

Theo đầu bài ta có: 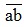 = 7(a + b) + 6

10a + b = 7a + 7b + 6

3a = 6b + 6

a = 2b + 2

a = 2(b + 1)

Mà 0 < a ≤ 9 ⇔ 0 < 2(b + 1) ≤ 9 ⇒ 0 < b + 1 < 4,5.

Do đó 0 ≤ b < 5.

Ta có bảng sau:

Vậy số cần tìm là 62 và 83.

................................

................................

................................

Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 6 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---