Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 2 Hình học có đáp án

---

---

Dưới đây là danh sách Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 2 Hình học có đáp án, cực sát đề chính thức. Hi vọng bộ đề thi này sẽ giúp bạn ôn luyện & đạt điểm cao trong các bài thi Toán lớp 12.

Bộ Đề thi 1 tiết Toán 12

• Đề kiểm tra 45 phút Toán 12 Chương 2 Hình học có đáp án (Đề 1)

• Đề kiểm tra 45 phút Toán 12 Chương 2 Hình học có đáp án (Đề 2)

• Đề kiểm tra 45 phút Toán 12 Chương 2 Hình học có đáp án (Đề 3)

• Đề kiểm tra 45 phút Toán 12 Chương 2 Hình học có đáp án (Đề 4)

Đề kiểm tra 45 phút Toán 12 Chương 2 Hình học (Đề số 1)

Thời gian làm bài: 45 phút

I. Trắc nghiệm ( 6 điểm)

Câu 1. Một hình hộp chữ nhật có ba kích thước là a, b,c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, b, c.

 

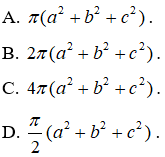
Câu 2. Một hình nón có đường cao h = 20cm, bán kính đáy r = 25cm. Tính diện tích xung quanh của hình nón đó:

 

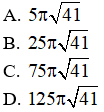
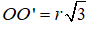
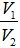
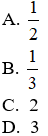
Câu 3. Một hình trụ có hai đáy là hai hình tròn (O;r) và (O';r). Khoảng cách giữa hai đáy là . Một hình nón có đỉnh là O’ và có đáy là hình tròn (O;r). Mặt xung quanh của hình nón chia khối trụ thành 2 phần. Gọi V₁ là thể tích phần bên ngoài khối nón, V₂ là phần thể tích bên trong khối nón. Khi đó bằng:

 

Câu 4. Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết diện đi qua trục là một hình vuông.

 

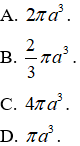
Câu 5. Cho hình lập phương ABCD.A'B'C'D' có độ dài mỗi cạnh là 10cm. Gọi O là tâm mặt cầu đi qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu là:

 

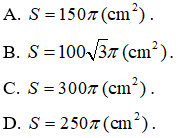
Câu 6. Trong không gian, cho tam giác ABC cân tại A, 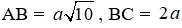. Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.

 

Câu 7. Một cái phễu rỗng phần trên có kích thước như hình vẽ. Diện tích xung quanh của phễu là:

 

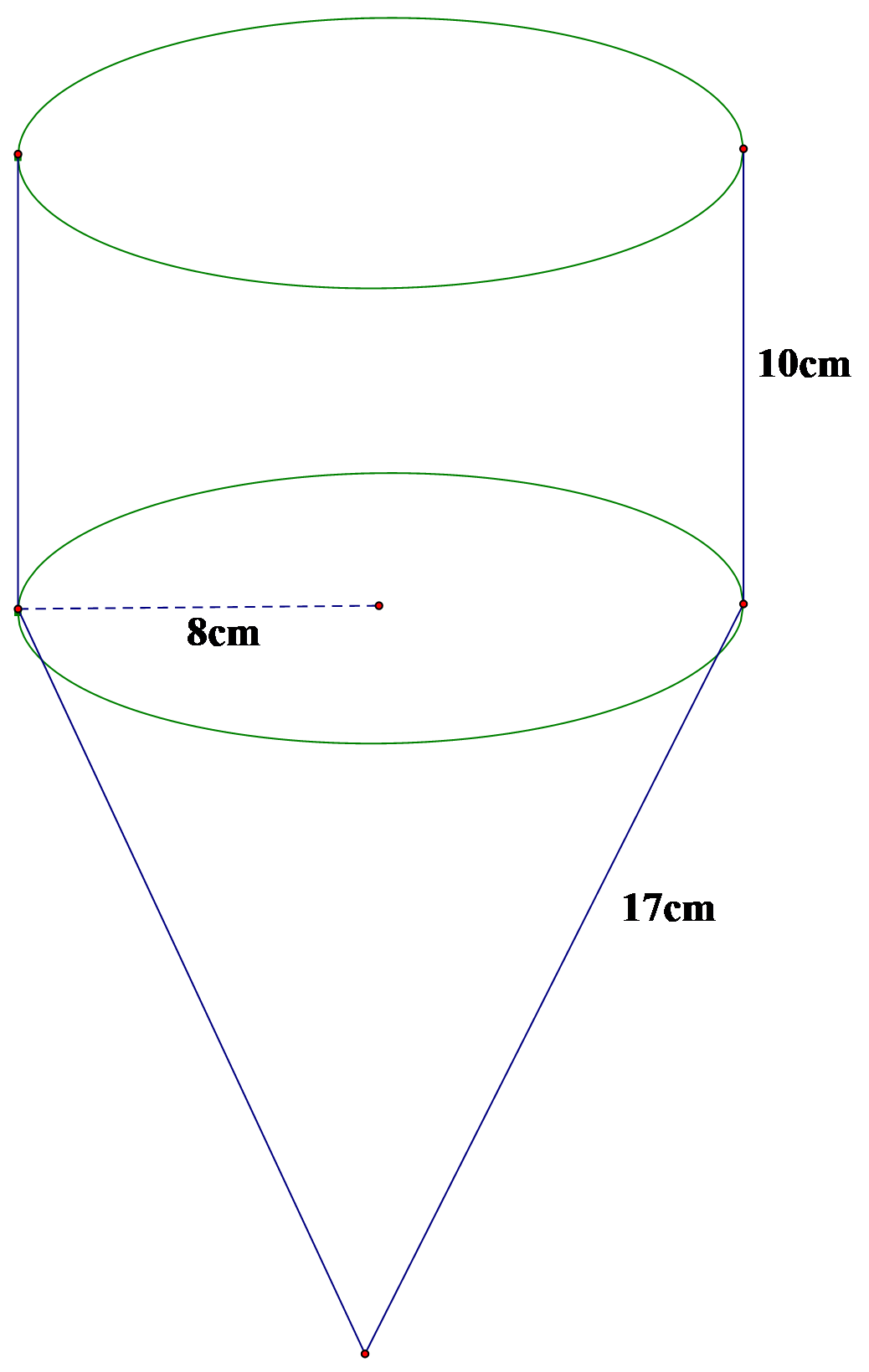
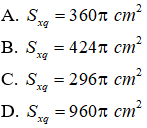
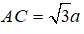
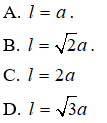
Câu 8. Trong không gian, cho tam giác ABC vuông tại A, AB = a và . Tính độ dài đường sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB.

 

II. Tự luận ( 4 điểm)

Câu 1. Tính bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a.

Câu 2. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD ?

Đáp án & Hướng dẫn giải

I. Trắc nghiệm ( 6 điểm)

Câu 1. Chọn A.

Tâm của mặt cầu chính là tâm của của hình hộp chữ nhật.

Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật.

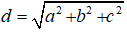
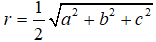
Mà độ dài đường chéo của hình chữ nhật là nên mặt cầu (S) có bán kính .

Do đó diện tích mặt cầu (S) là:

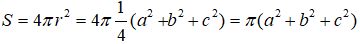
Câu 2. Chọn D

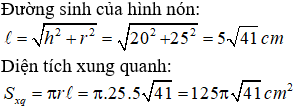
Câu 3. Chọn C.

Ta có hình vẽ minh họa như sau:

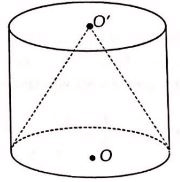
Ta có thể tích bên trong khối nón là:

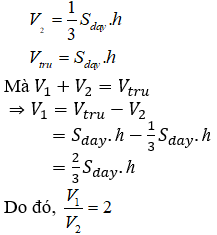
Câu 4. Chọn A.

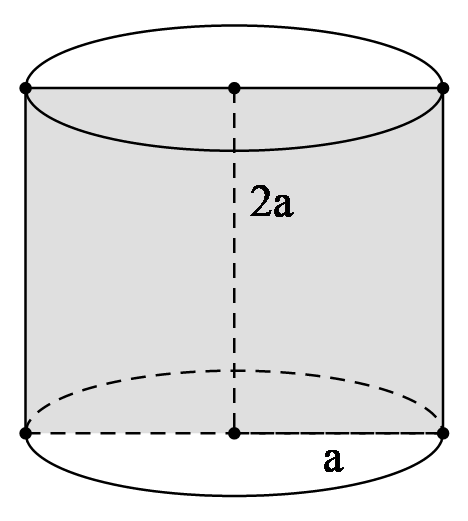
Theo bài ra thiết diện qua trục của hình trụ là hình vuông nên hình trụ có bán kính đáy là a, chiều cao 2a.

Do đó thể tích khối trụ là: V = πR²h = πa².2a = 2πa³.

Câu 5. Chọn C.

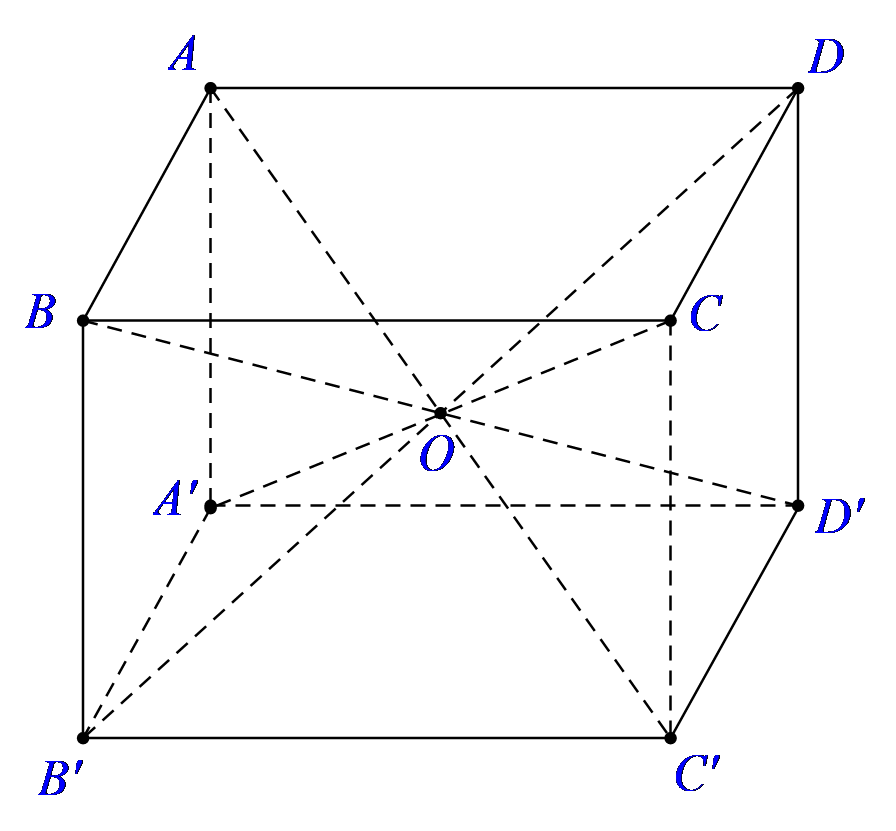
Dễ thấy tâm O của mặt cầu chính là tâm của hình lập phương.

Ta tính OA – bán kính mặt cầu.

Trong tam giác vuông ABC có: AC² = AB² + BC² = 200.

Trong tam giác vuông AA'C có:

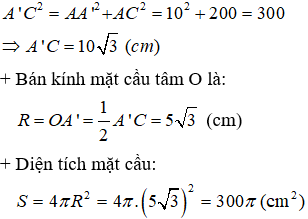
Câu 6. Chọn D

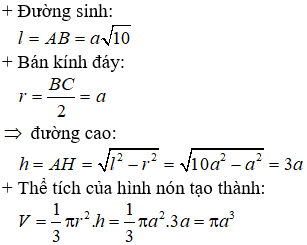
Câu 7. Chọn C.

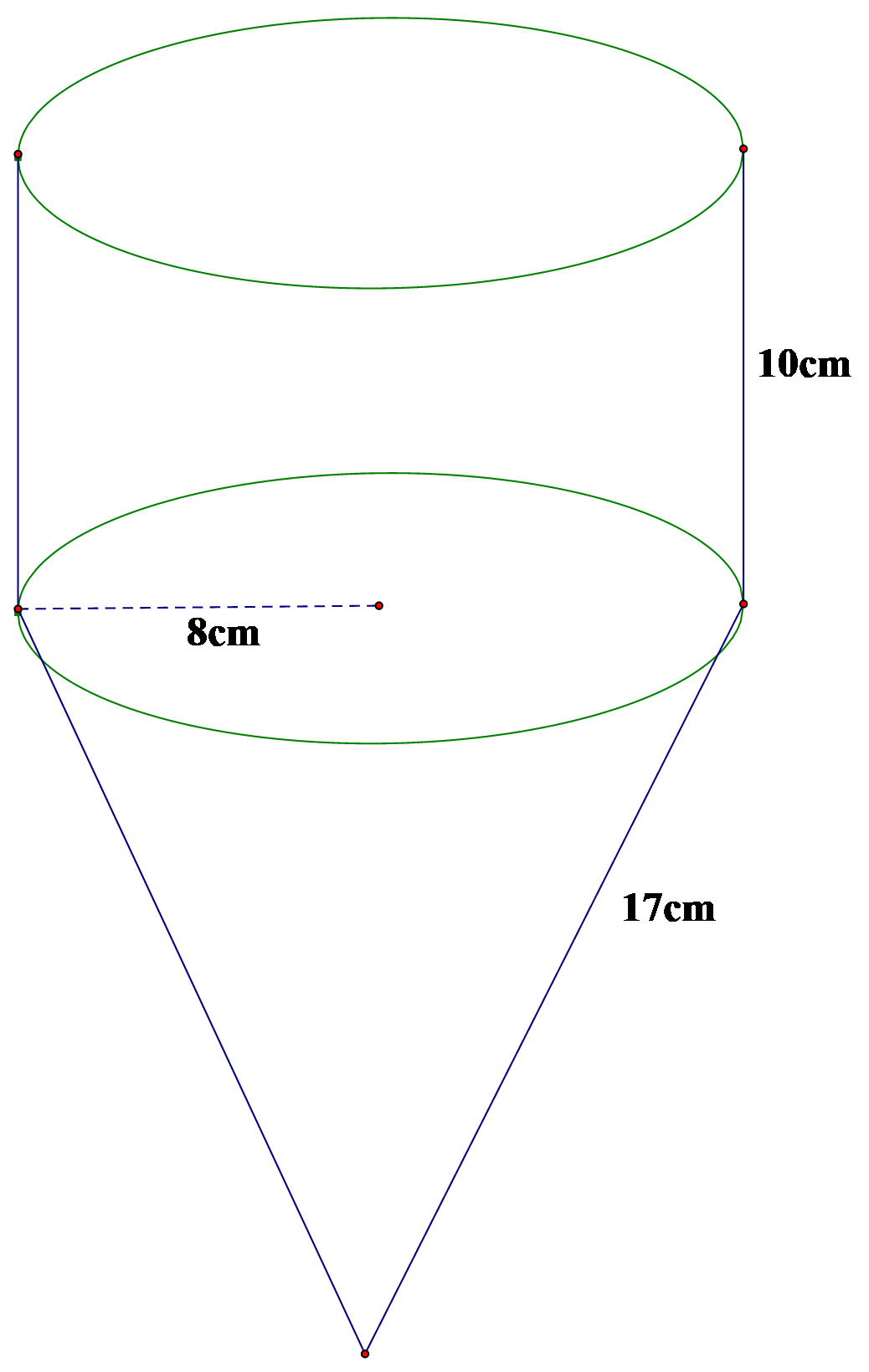
Ta tách phễu thành một hình nón có đường sinh l = 17 cm, bán kính đường tròn đáy R = 8 cm và một hình trụ có đường cao h = 10 cm, bán kính đáy là R = 8cm.

Diện tích xung quanh của hình trụ là:

 S_xq1 = 2πR.h = 2π.8.10 = 160π (cm²)

Diện tích xung quanh của hình nón là:

 S_xq2 = πR.l = π.8.17 = 136π (cm²)

Do đó, diện tích xung quang của phễu là:

 160π + 136π = 296π (cm²)

Câu 8. Chọn C.

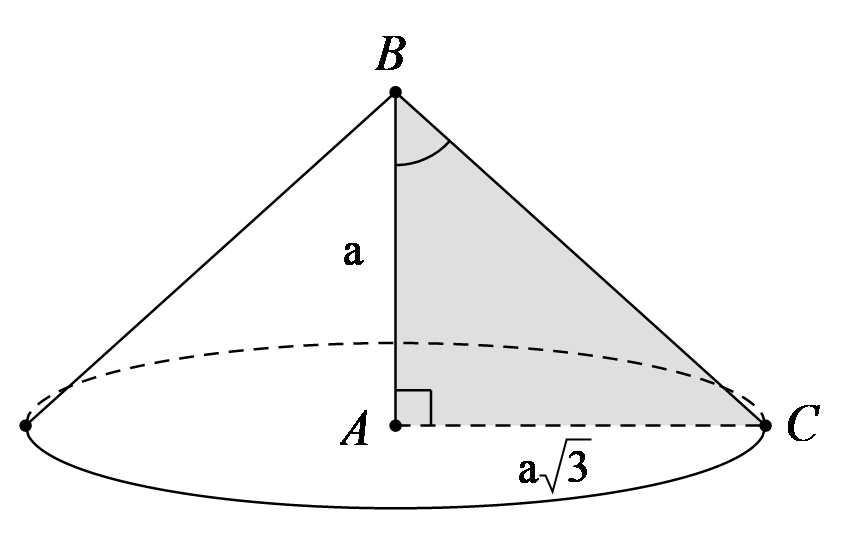
Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC.

Theo định lý Pytago thì:

 BC² = AB² + AC² = a² + 3a² = 4a² ⇒ BC = 2a

Vậy độ dài đường sinh của hình nón là l = 2a.

II. Tự luận ( 4 điểm)

Câu 1. Tính bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a.

Lời giải

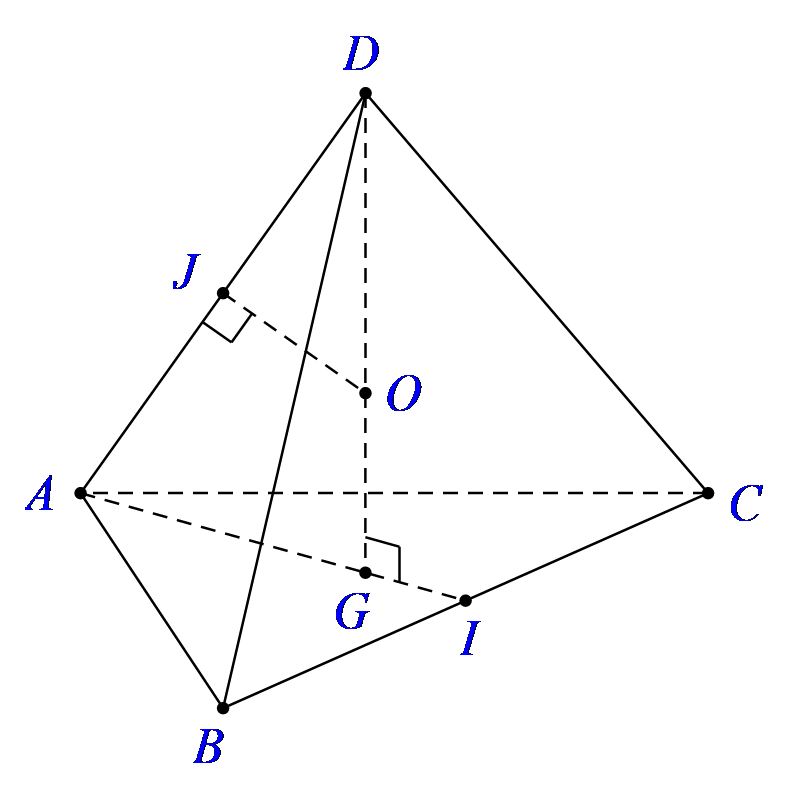
Gọi I là trung điểm cạnh BC, G là trọng tâm của tam giác ABC.

Ta có 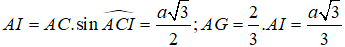và DG là trục của tam giác ABC.

Trong mp (DAG), kẻ trung trực của DA cắt DG tại O thì: OD = OA = OB = OC nên O chính là tâm mặt cầu ngoại tiếp tứ diện ABCD.

Bán kính R của mặt cầu bằng độ dài đoạn OD.

Trong tam giác ADG vuông tại G, ta có:

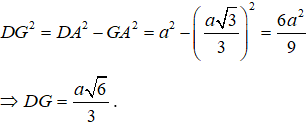
Mặt khác, tam giác DJO đồng dạng tam giác DGA nên:

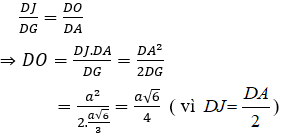
Vậy bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a là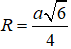

Câu 2. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD ?

Lời giải

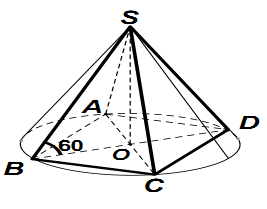
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)

Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)

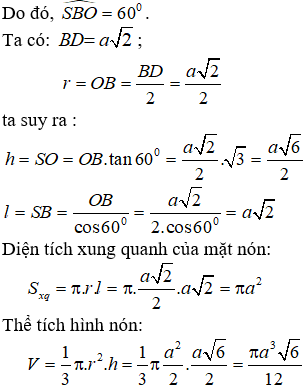
Đề kiểm tra 45 phút Toán 12 Chương 2 Hình học (Đề số 2)

Thời gian làm bài: 45 phút

I. Trắc nghiệm ( 6 điểm)

Câu 1. Cho mặt cầu S(O; R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Đường thẳng Δ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?

 A. d = R

 B. d > R

 C. d < R

 D. d ≠ R

Câu 2. Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:

 

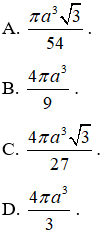
Câu 3. Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Tính diện tích xung quanh của hình nón.

 

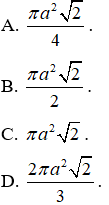
Câu 4. Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác ABC đều có cạnh bằng a, biết B, C thuộc đường tròn đáy. Thể tích của khối nón là:

 

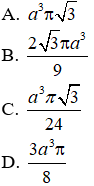
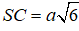
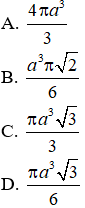
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:

 

Câu 6. Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức luôn đúng là?

 A. l = h

 B. R = h

 C. R² = h² + l²

 D. l² = h² + R²

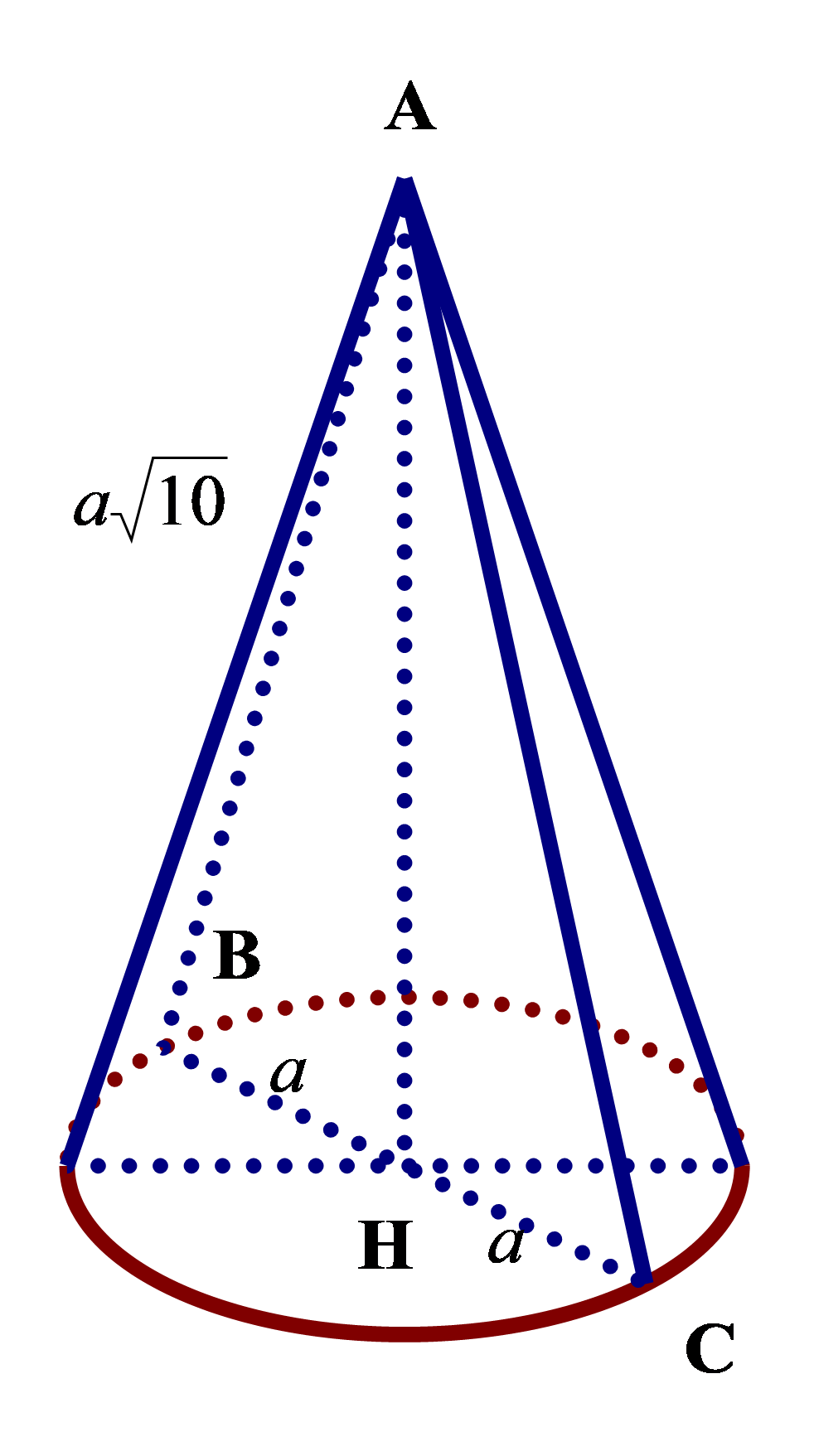
Câu 7. Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a, có diện tích xung quanh là:

 

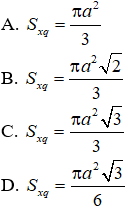
Câu 8. Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết diện đi qua trục là một hình vuông.

 

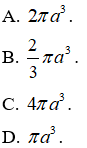
II. Tự luận ( 4 điểm)

Câu 1. Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng 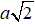và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh S_xq của hình nón và thể tích V của khối nón tương ứng là:

Câu 2. Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.

Đáp án & Hướng dẫn giải

I. Trắc nghiệm ( 6 điểm)

Câu 1. Chọn A.

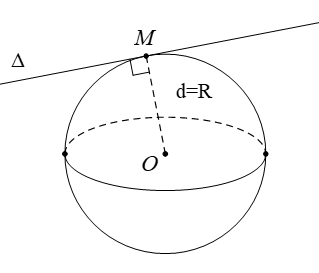
Đường thẳng Δ tiếp xúc với S( O; R) khi d = R.

Câu 2. Chọn C

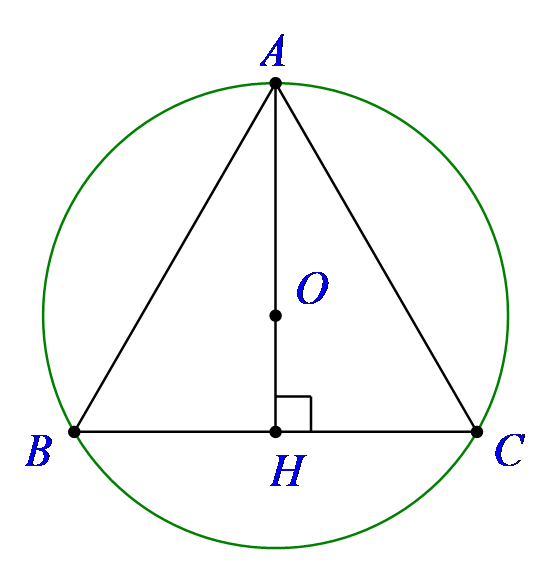
AH là đường cao trong tam giác đều cạnh a nên .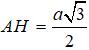

Gọi O là tâm mặt cầu ngoại tiếp ΔABC, thì O ∈ AH và .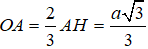

Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là .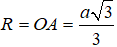

Vậy thể tích của khối cầu tương ứng là:

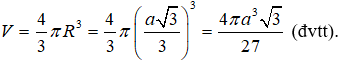
Câu 3. Chọn B.

Thiết diện qua trục là một tam giác vuông cạnh a nên đường sinh của hình nón là l = a.

Đường kính của đường tròn đáy là: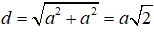

và bán kính đáy là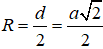

Diện tích xung quanh của hình nón là .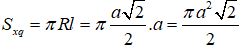

Câu 4. Chọn C.

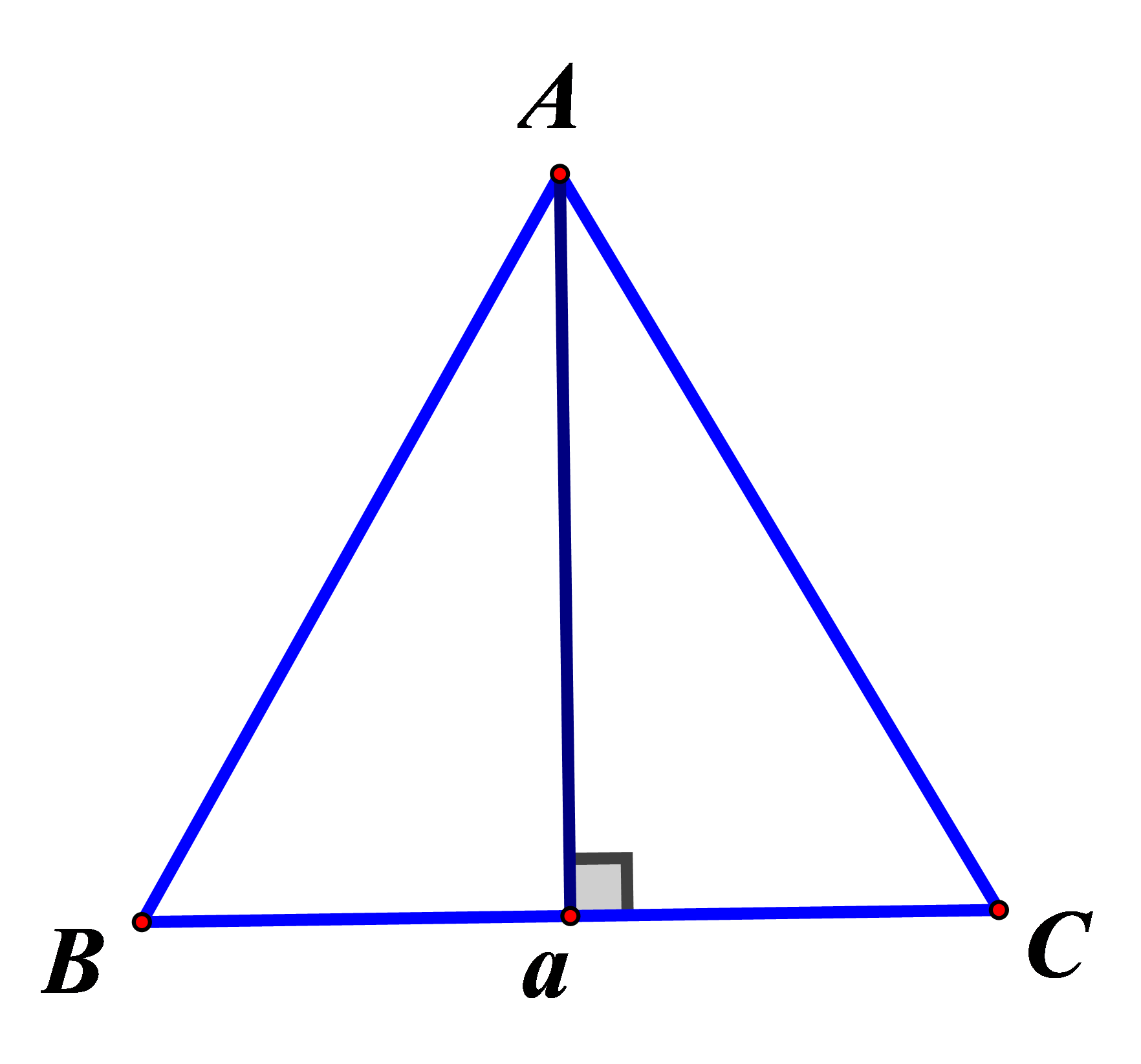
Bán kính đáy khối nón là .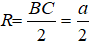

Chiều cao khối nón là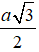

(chính là chiều cao của tam giác đều cạnh a)

Suy ra, thể tích của khối nón là:

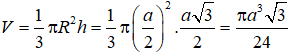
Câu 5. Chọn A.

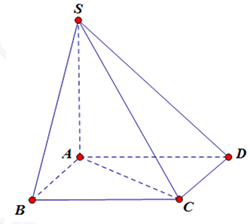
Ta có:

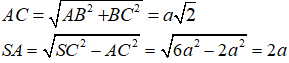
Hình nón tròn xoay được tạo thành là một hình nón có bán kính đáy là R = AC, đường cao h = SA có thể tích là:

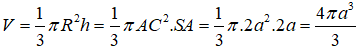
Câu 6. Chọn A.

Đường sinh và chiều cao của một hình trụ luôn bằng nhau nên đẳng thức đúng là l = h

Câu 7. Chọn C.

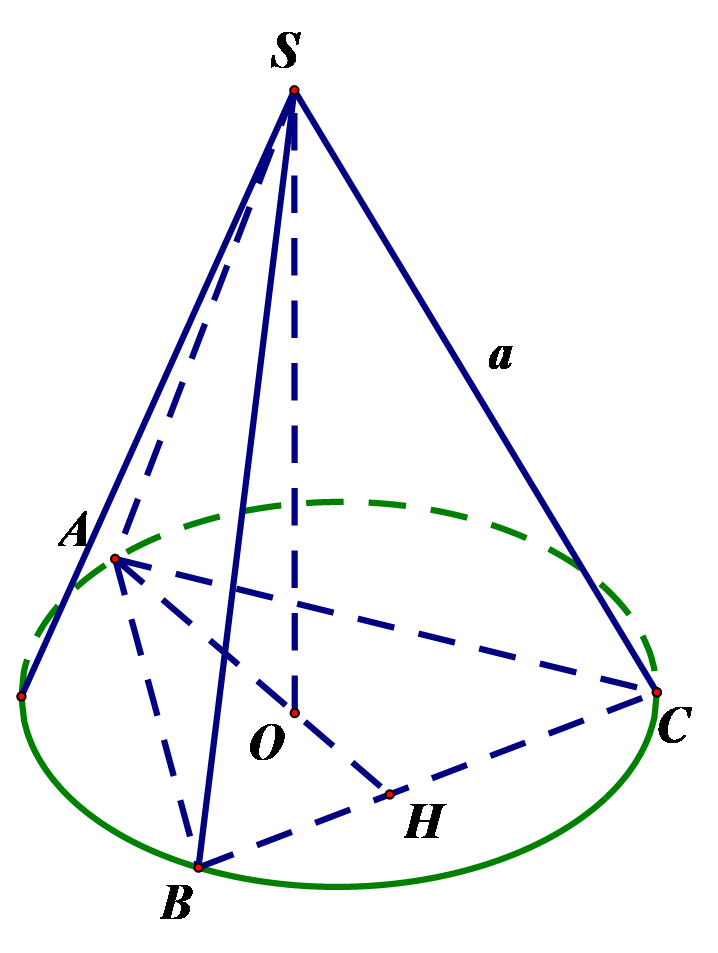
Khi đó, SO là trục của tam giác ABC nên SO⊥(ABC)

Gọi AO ∩ BC = H

Ta có:

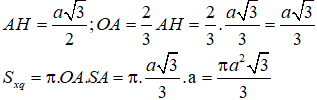
Câu 8. Chọn A.

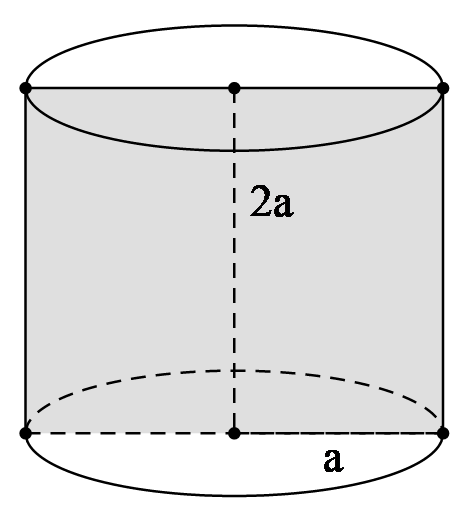
Theo bài ra thiết diện qua trục của hình trụ là hình vuông nên hình trụ có bán kính đáy là a, chiều cao 2a.

Do đó thể tích khối trụ là: V = πR²h = πa².2a = 2πa³.

II. Tự luận ( 4 điểm)

Câu 1. Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng 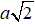và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh S_xq của hình nón và thể tích V của khối nón tương ứng là:

Lời giải

Gọi A là một điểm thuộc đường tròn đáy hình nón.

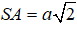
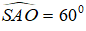
Theo giải thiết ta có đường sinh và góc giữa đường sinh và mặt phẳng đáy là .

Trong tam giác vuông SAO, ta có:

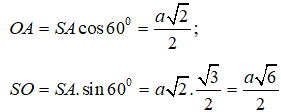
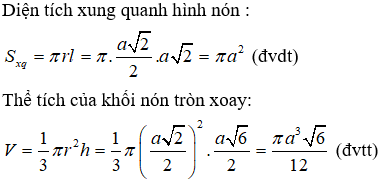
Câu 2. Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.

Lời giải

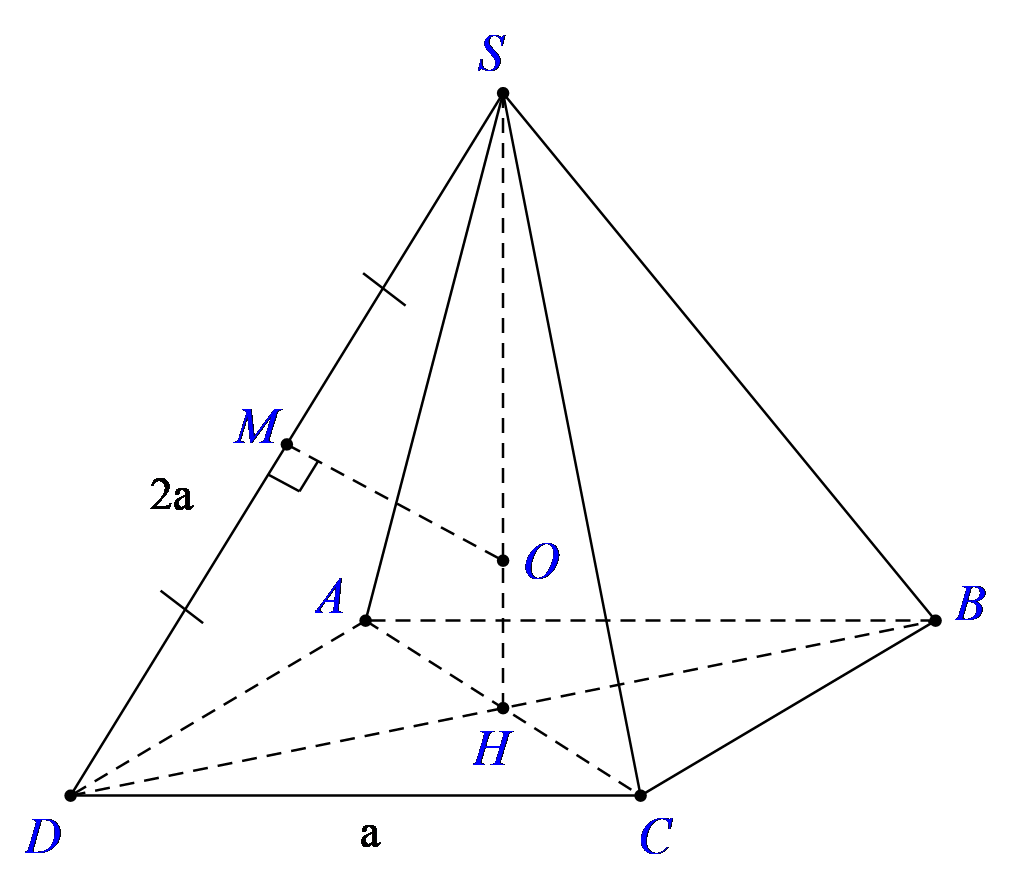
Cho hình chóp tứ giác đều S.ABCD.

Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.

Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)

Mà O thuộc trục SH của hình vuông ABCD nên:

OA = OB = OC = OD (2)

Từ (1) và (2) suy ra: OA = OB = OC = OD = OS

Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO

Ta có:

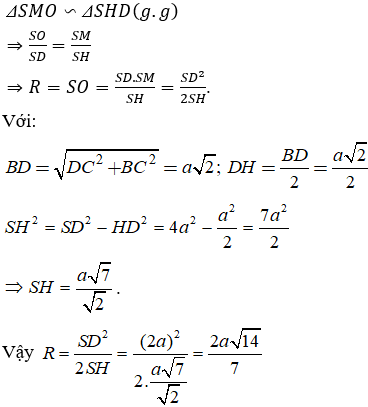
Xem thêm các bài thi Toán lớp 12 chọn lọc, có đáp án hay khác:

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 1 Giải tích có đáp án

• Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 1 Giải tích có đáp án

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 2 Giải tích có đáp án

• Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 2 Giải tích có đáp án

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án

• Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 1 Hình học có đáp án

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 2 Hình học có đáp án

• Top 4 Đề thi Toán 12 Học kì 1 năm 2024 có đáp án

---

---

---