Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 1 Giải tích có đáp án

---

---

Dưới đây là danh sách Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 1 Giải tích có đáp án, cực sát đề chính thức. Hi vọng bộ đề thi này sẽ giúp bạn ôn luyện & đạt điểm cao trong các bài thi Toán lớp 12.

Bộ Đề thi 1 tiết Toán 12

• Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 1)

• Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 2)

• Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 3)

• Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 4)

Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích (Đề số 1)

Thời gian làm bài: 45 phút

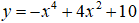
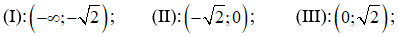
Câu 1. Cho hàm số và các khoảng sau:

Hỏi hàm số đồng biến trên các khoảng nào?

 A. Chỉ (I).

 B. (I) và (II).

 C. (II) và (III).

 D. (I) và (III).

Câu 2. Cho hàm số 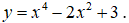Khẳng định nào sau đây là đúng?

 A. Hàm số có ba điểm cực trị.

 B. Hàm số chỉ có đúng 2 điểm cực trị.

 C. Hàm số không có cực trị.

 D. Hàm số chỉ có đúng một điểm cực trị.

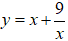
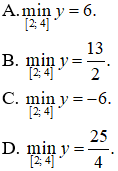
Câu 3. Giá trị nhỏ nhất của hàm số trên đoạn [2; 4] là:

 

Câu 4. Cho hàm số y = f(x) có đạo hàm 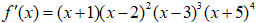. Hỏi hàm số y= f(x) có mấy điểm cực trị?

 A. 2.

 B. 3.

 C. 4.

 D. 5.

Câu 5. Đồ thị hàm số 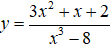có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

 A. y = 2 và x = 0.

 B. x = 2 và y = 0.

 C. x = 2 và y = 3.

 D. y = 2 và x = 3.

Câu 6. Cho đồ thị hàm số y = f(x) như hình bên. Khẳng định nào sau đây là đúng?

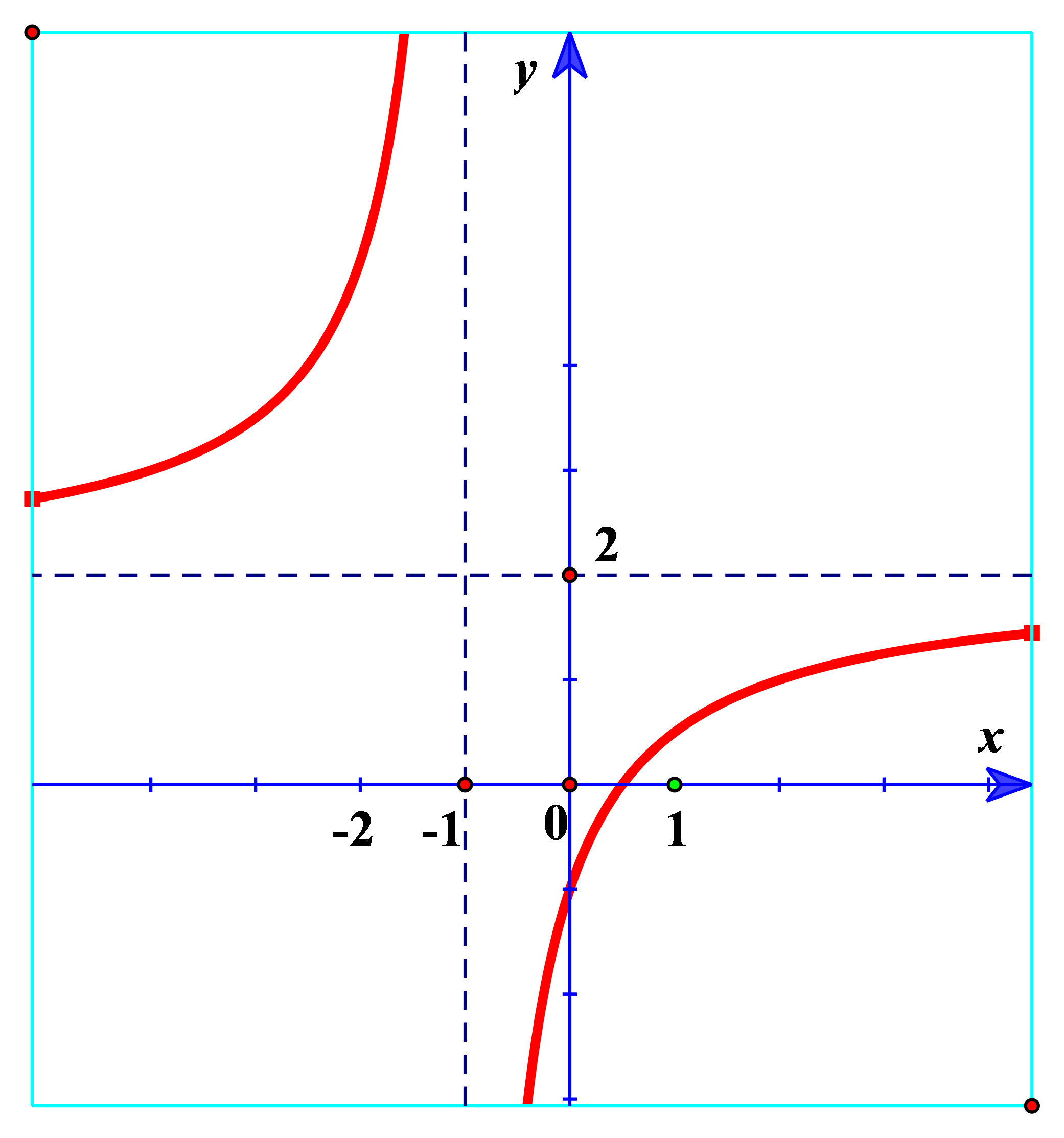
 A. Đồ thị hàm số có tiệm cận đứng x = -1, tiệm cận ngang y = 2.

 B. Hàm số nghịch biến trong khoảng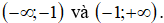

 C. Hàm số có hai cực trị.

 D. Hàm số đồng biến trong khoảng (-∞;+∞).

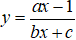
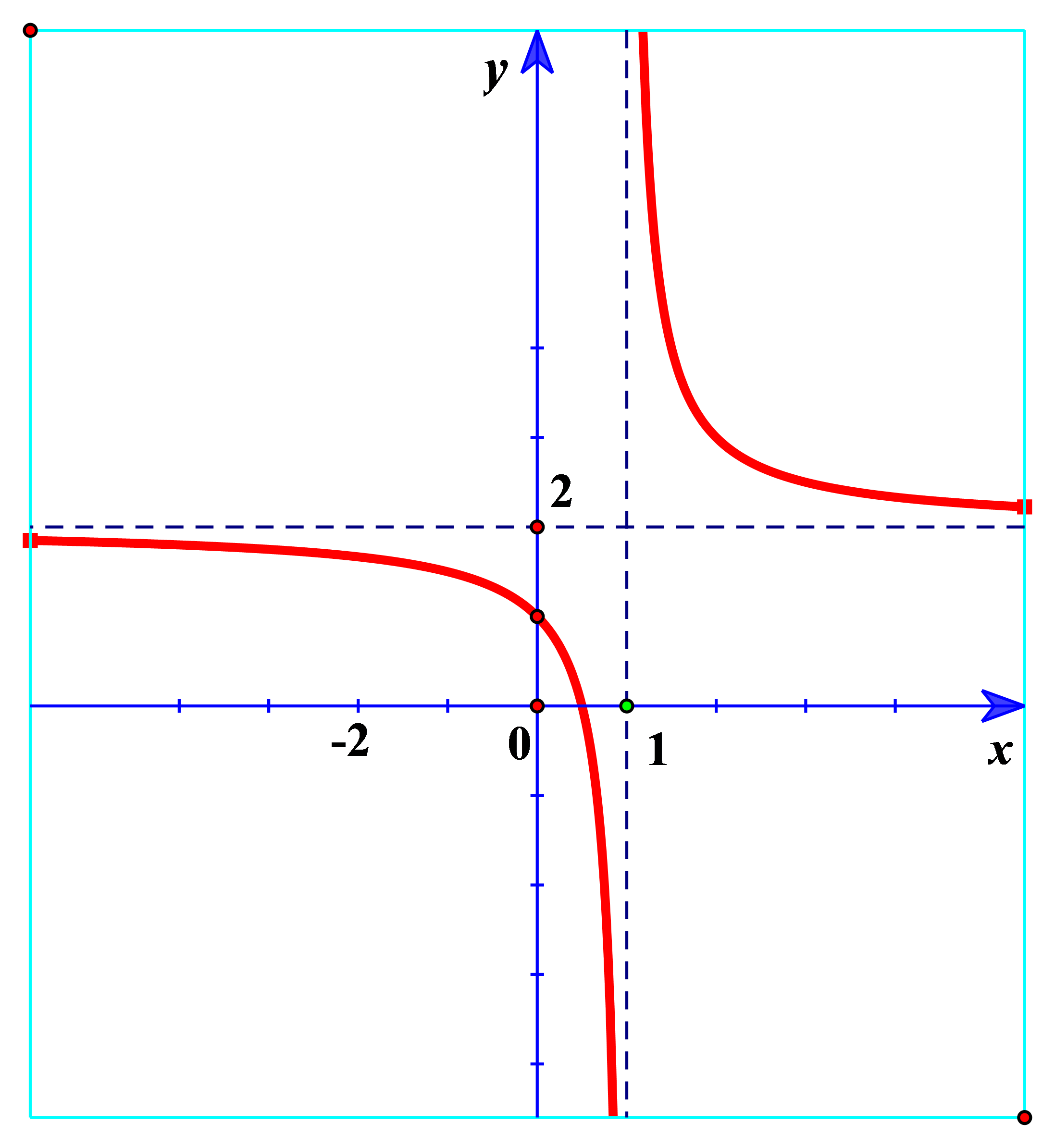
Câu 7. Xác định a, b, c để hàm số có đồ thị như hình vẽ bên. Chọn đáp án đúng?

 A. a = 2; b = -1; c = 1

 B. a = 2; b = 1; c = 1

 C. a = 2; b = 2; c = -1

 D. a = 2; b = 1; c = -1

Câu 8. Cho hàm số 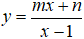có đồ thị (C). Biết tiệm cận ngang của (C) đi qua điểm A(-1; 2) đồng thời điểm I(2; 1) thuộc (C). Khi đó giá trị của m + n là

 A. m + n = -1.

 B. m + n = 1.

 C. m + n = -3.

 D. m + n = 3 .

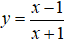
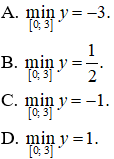
Câu 9. Giá trị nhỏ nhất của hàm số trên đoạn [0; 3] là:

 

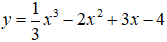
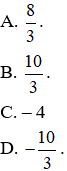
Câu 10. Giá trị lớn nhất của hàm số trên đoạn [1; 5] là:

 

Câu 11. Giá trị của m để đồ thị hàm số 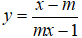không có tiệm cận đứng là

 A. m = 0; m = ±1.

 B. m = -1

 C. m = ±1 .

 D. m = 1

Câu 12. Tọa độ giao điểm giữa đồ thị 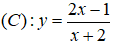và đường thẳng d: y = x - 2 là

 A. A(-1; -3); B(3; 1)

 B. A(1; -1); B(0; -2)

 C. A(-1; -3); B(0; -2)

 D. A(1; -1); B(3; 1)

Câu 13. Cho hàm số 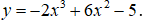Phương trình tiếp tuyến của (C) tại điểm M thuộc (C) và có hoành độ bằng 3

 A. y = 18x + 49

 B. y = -18x- 49

 C. y = -18x + 49

 D. y= 18x- 49

Câu 14. Tập tất cả các giá trị của tham số m để đường thẳng d: y = x + m2 cắt đồ thị hàm số (C): y = -x3 + 4x tại ba điểm phân biệt là

 

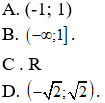
Câu 15. Cho hàm số 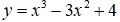có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là

 A. {0}

 B. R

 C. {-3}

 D. (-3; +∞).

Câu 16. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 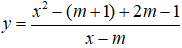tăng trên từng khoảng xác định của nó?

 A. m > 1

 B. m ≤ 1

 C. m < 1

 D. m ≥ 1

Câu 17. Hàm số 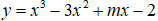đạt cực tiểu tại x = 2 khi?

 A. m > 0

 B. m ≠ 0

 C. m = 0

 D. m < 0

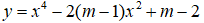
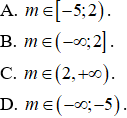
Câu 18. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng (1; 3)?

 

Câu 19. Cho hàm số Tìm tất cả các giá trị thực của m để hàm số có 2 cực trị cùng dấu .

 

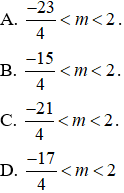
Câu 20. Một hợp tác xã nuôi cá thí nghiệm trong hồ. Người ta thấy rằng nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng P(n) = 480 - 20n (gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều gam cá nhất?

 A. 12.

 B. 24.

 C. 6.

 D. 32.

Đáp án & Hướng dẫn giải

Câu 1. Chọn D.

TXĐ: D = R

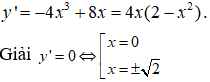
Trên các khoảng 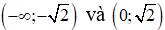, y’ > 0 nên hàm số đồng biến

Câu 2. Chọn A

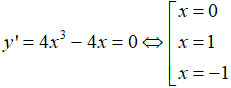
y(0) = 3; y(1) = y(-1) = 2 nên hàm số có ba cực trị.

Câu 3. Chọn A.

Nhận xét: Hàm số đã cho liên tục trên [2;4]

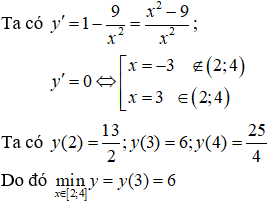
Câu 4. Chọn A

Do f’(x) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.

Câu 5. Chọn B

Ta có: 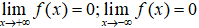nên đồ thị hàm số có tiệm cận ngang y = 0

Và 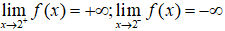nên đồ thị hàm số có tiệm cận đứng là x = 2.

Câu 6. Chọn A.

Nhìn vào ta thấy đồ thị có tiệm cận đứng x = - 1 tiệm cận ngang y = 2.

Câu 7. Chọn D.

Dựa vào đồ thị, ta có tiệm cận đứng x = 1, tiệm cận ngang y = 2 và đồ thị đi qua điểm (0; 1) nên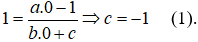

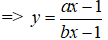
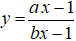
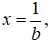
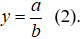
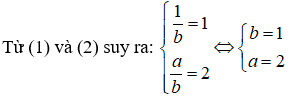
Đồ thị hàm số có tiệm cận đứng tiệm cận ngang

Câu 8. Chọn A

Để hàm số có đường tiệm cận ngang thì x = 1 không là nghiệm của tử thức

=> m + n ≠ 0

Khi đó tiệm cận ngang của đồ thị hàm số là y = m.

Do tiệm cận ngang của (C) đi qua A( - 1; 2) nên m = 2 .

Mặt khác đồ thị hàm số đi qua điểm I(2; 1) nên có:

 

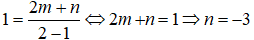
Vậy m + n = 2 + (-3) = -1.

Câu 9. Chọn C.

Nhận xét: Hàm số đã cho liên tục trên [0;3]

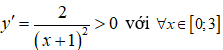
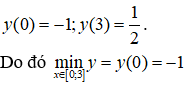
Ta có nên hàm số đồng biến trên [0; 3].

Câu 10. Chọn A.

TXĐ: D = R.

Ta có:

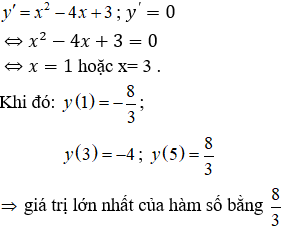
Câu 11. Chọn A

Xét m = 0 thì đồ thị hàm số là đường thẳng y = -x là 1 đường thẳng nên không có đường tiệm cận đứng.

Xét m ≠ 0 khi đó đồ thị hàm số không có đường tiệm cận đứng nếu 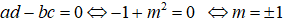(khi đó hàm số suy biến có đạo hàm y’ = 0)

Vậy giá trị của m cần tìm là m = 0; m = ±1.

Câu 12. Chọn A.

Lập phương trình hoành độ giao điểm:

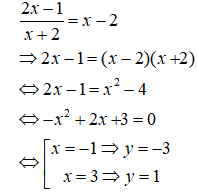
Câu 13. Chọn C

Ta có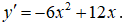

Với x₀ = 3 ⇒ y₀ = -5 ⇒ M(3;-5) và hệ số góc k = y'(3) = -18.

Vậy phương trình tiếp tuyến tại M là :

y = -18(x - 3) - 5 = -18x + 49.

Câu 14. Chọn D.

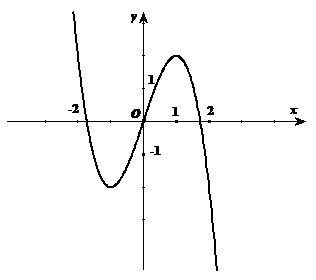
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:

 

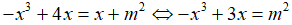
Ta khảo sát hàm số (C): y = -x3 + 3x có đồ thị sau như hình bên.

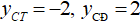
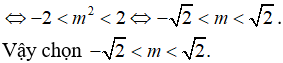
Tìm được nên yêu cầu bài toán

Câu 15. Chọn D.

Phương trình đường thẳng d có hệ số góc k và đi qua I(1; 2) là d: y = k(x - 1) + 2.

Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:

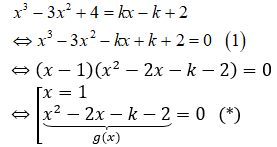
Để d cắt (C) tại ba điểm phân biệt ⇔ Phương trình (*) có hai nghiệm phân biệt x₁; x₂ khác 1.

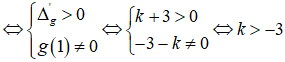
Hơn nữa theo Viet ta có 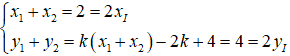nên I là trung điểm AB.

Vậy chọn k > -3, hay k ∈ (-3;+∞).

Câu 16. Chọn B.

Tập xác định: D = R\ {m}.

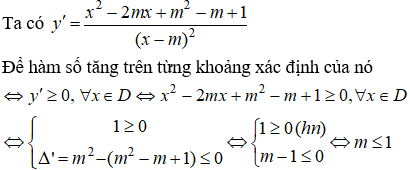
Câu 17. Chọn C

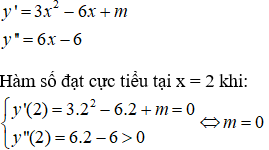
Câu 18. Chọn B.

Tập xác định D = R.

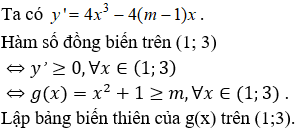
Dựa vào bảng biến thiên, kết luận: m ≤ min ⁡g(x) ⇔ m ≤ 2

Câu 19. Chọn D

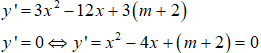
Hàm số có 2 điểm cực trị x₁; x₂ ⇔ Δ' > 0 ⇔ 4 - (m + 2) > 0 ⇔ m < 2

Chia y cho y’ ta được :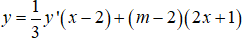

Suy ra : Phương trình đường thẳng đi qua hai điểm cực trị là: y = (m - 2)(2x + 1).

Điểm cực trị tương ứng : A(x₁;(m - 2)(2x₁ + 1)) và B(x₂;(m - 2)(2x₂ + 1))

Có: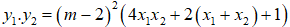

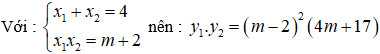
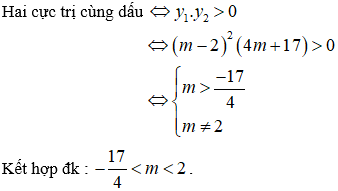
Câu 20. Chọn A.

Sau một vụ, trung bình số cá trên mỗi đơn vị diện tích mặt hồ cân nặng:

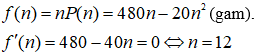
Bảng biến thiên:

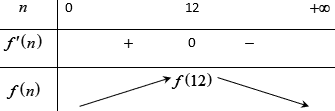
Trên mỗi đơn vị diện tích của mặt hồ, cần thả 12 con cá thì sau một vụ thu hoạch được nhiều gam cá nhất.

Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích (Đề số 2)

Thời gian làm bài: 45 phút

Câu 1. Cho hàm số 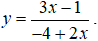Khẳng định nào sau đây là khẳng định đúng?

 A. Hàm số luôn nghịch biến trên R.

 B. Hàm số luôn nghịch biến trên từng khoảng xác định.

 C. Hàm số đồng biến trên các khoảng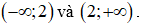

 D. Hàm số nghịch biến trên các khoảng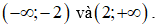

Câu 2. Cho hàm số 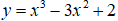. Khẳng định nào sau đây là đúng?

 A. Hàm số đạt cực đại tại x =2 và đạt cực tiểu tại x = 0.

 B. Hàm số đạt cực tiểu tại x = 2 và đạt cực đại x = 0.

 C. Hàm số đạt cực đại tại x = -2 và cực tiểu tại x = 0.

 D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = - 2.

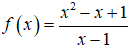
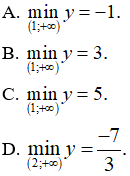
Câu 3. Giá trị nhỏ nhất của hàm số trên khoảng (1;+∞) là:

 

Câu 4. Cho hàm số 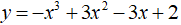. Khẳng định nào sau đây là khẳng định đúng?

 A. Hàm số luôn nghịch biến trên R.

 B. Hàm số nghịch biến trên các khoảng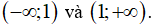

 C. Hàm số đồng biến trên khoảng và nghịch biến trên khoảng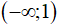

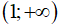
 D. Hàm số luôn đồng biến trên R.

Câu 5. Giá trị cực tiểu của hàm số 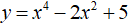là:

 A. 5

 B. 4

 C. 0

 D. 1

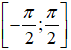
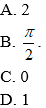
Câu 6. Hàm số y = sinx + 1 đạt giá trị lớn nhất trên đoạn bằng:

 

Câu 7. Số đường tiệm cận của đồ thị hàm số 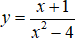là:

 A. 4.

 B. 2.

 C. 1.

 D. 3.

Câu 8. Số tiệm cận của hàm số 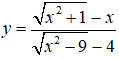là

 A. 2

 B. 4

 C. 3

 D. 1

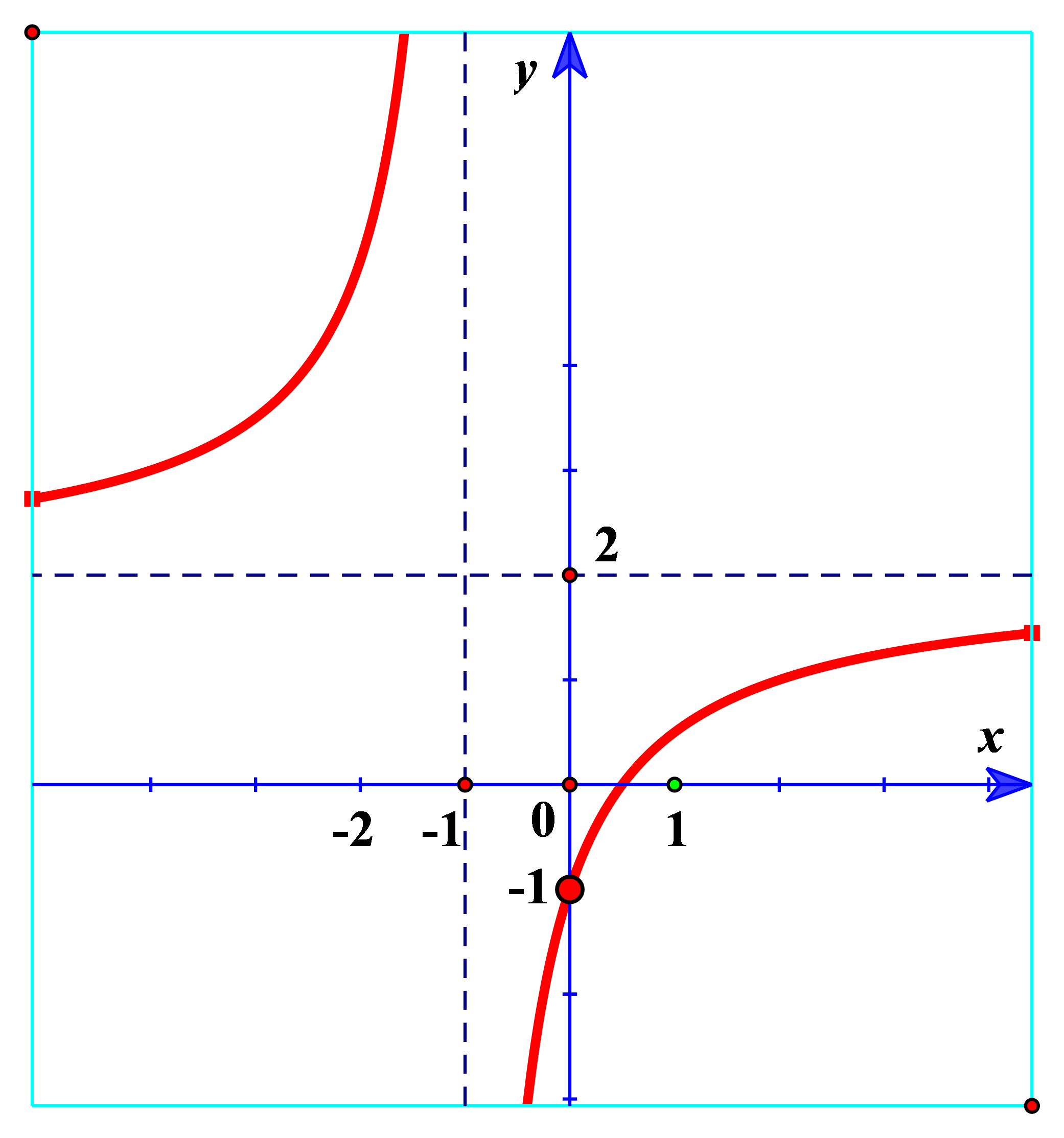
Câu 9. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

 

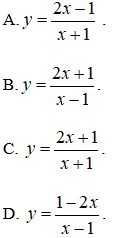
Câu 10. Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

 

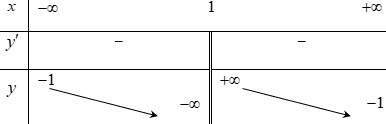
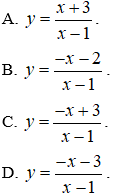
Câu 11. Bảng biến thiên sau đây là của một trong 4 hàm số được liệt kê dưới đây. Hỏi đó là hàm số nào?

 

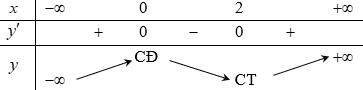
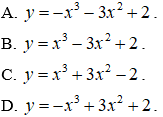
Câu 12. Cho hàm số 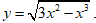. Khẳng định nào sau đây là khẳng định sai?

 

Câu 13. Cho hàm số 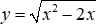. Khẳng định nào sau đây là đúng

 A. Hàm số có hai điểm cực trị.

 B. Hàm số đạt cực tiểu tại x = 0.

 C. Hàm số đạt cực đại x = 2.

 D. Hàm số không có cực trị.

Câu 14. Đường thẳng y = x - 1 cắt đồ thị hàm số 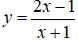tại các điểm có tọa độ là

 A. (0; 2)

 B. (-1; 0); (2; 1)

 C. (0; -1); (2; 1)

 D. (1; 2)

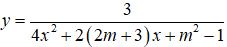
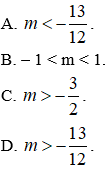
Câu 15. Xác định m để đồ thị hàm số có đúng hai tiệm cận đứng.

 

Câu 16. Cho hàm số 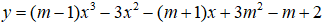. Để hàm số có cực đại, cực tiểu thì:

 A. m = 1

 B. m ≠ 1

 C. m > 1

 D. m tùy ý.

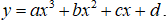
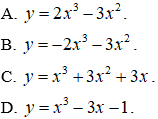
Câu 17. Cho hàm số Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A(-1; -1) thì hàm số có phương trình là:

 

Câu 18. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 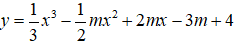nghịch biến trên một đoạn có độ dài là 3?

 A. m = -1; m = 9.

 B. m = -1

 C. m = 9

 D. m = 1; m = -9

Câu 19. Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là 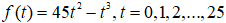. Nếu coi f(t) là hàm số xác định trên đoạn [0;25] thì đạo hàm f’(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định ngày mà tốc độ truyền bệnh là lớn nhất?

 A. Ngày thứ 19.

 B. Ngày thứ 5.

 C. Ngày thứ 16.

 D. Ngày thứ 15.

Câu 20. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 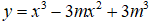có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48.

 A. m = 2 hoặc m = 0.

 B. m = 2

 C. m = -2

 D. m = ±2

Đáp án & Hướng dẫn giải

Câu 1. Chọn B.

TXĐ: D = R\{2}.

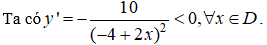
Do đó, hàm số đã cho nghịch biến trên từng khoảng xác định.

Câu 2. Chọn B

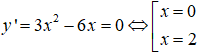
Lập bảng biến thiên ta được hàm số đạt cực đại tại x= 0 và đạt cực tiểu tại x= 2

Câu 3. Chọn B.

Hàm số xác định với ∀ x ∈ (1;+∞)

Nhận xét: Hàm số f(x) liên tục trên (1;+∞)

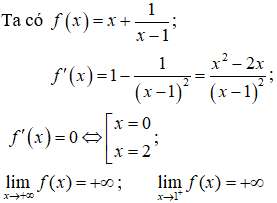
Bảng biến thiên

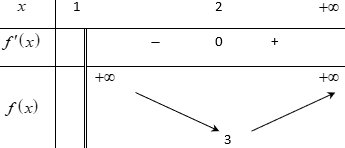
Từ bảng biến thiên ta có: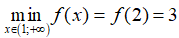

Câu 4. Chọn A.

TXĐ: D = R.

Ta có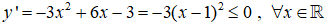

Do đó, hàm số đã cho nghịch biến trên R.

Câu 5. Chọn B

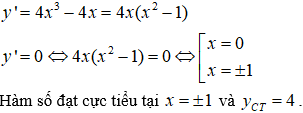
Câu 6. Chọn A.

TXĐ: D = R.

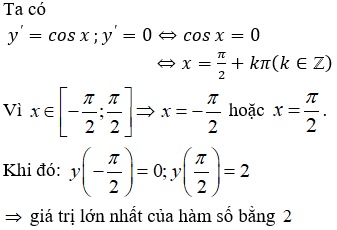
Câu 7. Chọn D

Tiệm cận đứng là x = ±2 và tiệm cận ngang là y = 0

→ Số đường tiệm cận là 3

Câu 8. Chọn B

Điều kiện xác định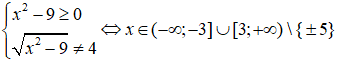

Khi đó có: 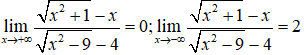nên đồ thị hàm số có hai đường tiệm cận ngang.

Mặt khác có 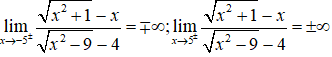nên đồ thị hàm số có hai đường tiệm cận đứng.

Vậy đồ thị hàm số đã cho có 4 đường tiệm cận.

Câu 9. Chọn A.

Nhìn vào đồ thị ta thấy ngay tiệm cận đứng x = -1, tiệm cận ngang y = 2. Loại B, D.

Đồ thị hàm số đi qua điểm (0;-1).

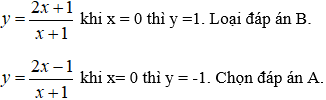
Câu 10. Chọn C.

Nhìn vào bảng biến thiên ta thấy ngay tiệm cận đứng x = 1 , tiệm cận ngang y = -1. suy ra loại đáp án A.

Nhìn vào bảng biến thiên, hàm số nghịch biến trên các khoảng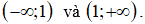

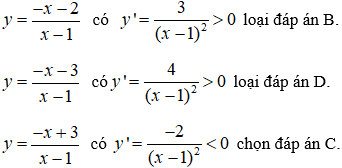
Câu 11. Chọn B.

Dựa vào bảng biến thiên ta thấy hệ số a > 0 nên ta loại phương án A và D.

Phương trình y’ = 0 có hai nghiệm là x = 0 hoặc x = 2 nên chỉ có phương án B là phù hợp.

Câu 12. Chọn B.

Điều kiện xác định: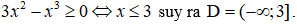

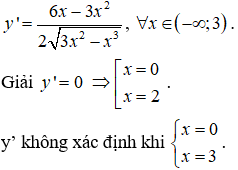
Bảng biến thiên:

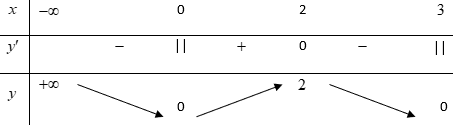
Hàm số nghịch biến (-∞;0) và (2;3). Hàm số đồng biến (0;2).

Câu 13. Chọn D

TXĐ: D = (-∞;0] ∪ [2;+∞).

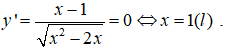
y’ không đổi dấu trên các khoảng xác định nên hàm số không có cực trị.

Câu 14. Chọn C

Phương trình hoành độ giao điểm của 2 đồ thị hàm số:

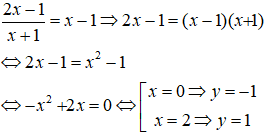
Vậy đường thẳng d cắt đồ thị hàm số (C) tại 2 điểm phân biệt là ( 0; -1) và (2;1).

Câu 15. Chọn D

Đồ thị hàm số 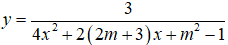có đúng hai tiệm cận đứng

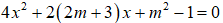
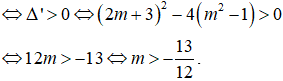
⇔ phương trình có hai nghiệm phân biệt

Câu 16. Chọn B

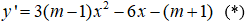
Để hàm số có cực đại, cực tiểu thì phương trình (*) có 2 nghiệm phân biệt:

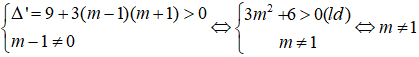
Câu 17. Chọn B

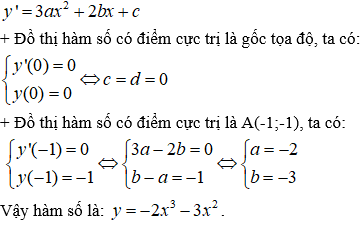
Câu 18. Chọn A.

Tập xác định: D = R. Ta có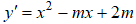

Ta không xét trường hợp y' ≤ 0, ∀ x ∈ R vì a = 1> 0.

Hàm số nghịch biến trên một đoạn có độ dài là 3 ⇔ y' = 0 có 2 nghiệm x₁; x₂ thỏa mãn:

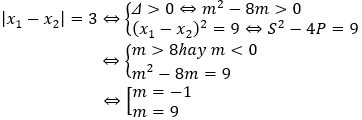
Câu 19. Chọn D.

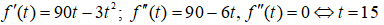
Bảng biến thiên

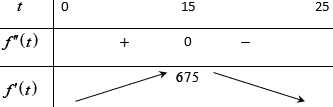
Tốc độ truyền bệnh lớn nhất là vào ngày thứ 15.

Câu 20. Chọn D

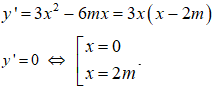
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi : 2m ≠ 0 ⇔ m ≠ 0 (1)

Khi đó, các điểm cực trị của đồ thị hàm số là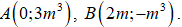

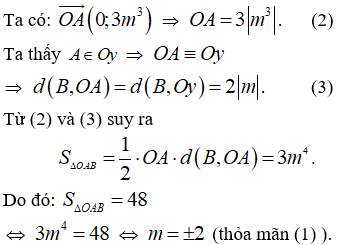
Xem thêm các bài thi Toán lớp 12 chọn lọc, có đáp án hay khác:

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 1 Giải tích có đáp án

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 2 Giải tích có đáp án

• Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 2 Giải tích có đáp án

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án

• Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 1 Hình học có đáp án

• Top 4 Đề kiểm tra 15 phút Toán 12 Chương 2 Hình học có đáp án

• Top 4 Đề kiểm tra 1 tiết Toán 12 Chương 2 Hình học có đáp án

• Top 4 Đề thi Toán 12 Học kì 1 năm 2024 có đáp án

---

---

---