Công thức tính thể tích khối chóp hay, nhanh nhất (siêu hay)

Công thức tính thể tích khối chóp hay, nhanh nhất (siêu hay)

Công thức tính thể tích khối chóp Toán lớp 12 sẽ giúp học sinh nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 12.

Bài viết Công thức tính thể tích khối chóp gồm 3 phần: Lí thuyết, Công thức các dạng và Luyện tập áp dụng công thức trong bài có lời giải chi tiết giúp học sinh dễ học, dễ nhớ Công thức tính thể tích khối chóp Toán 12.

1. Lí thuyết

- Định nghĩa hình chóp: Hình chóp là một hình có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này được gọi là đỉnh của chóp.

- Có 2 loại chóp phổ biến là chóp tam giác và chóp tứ giác

         

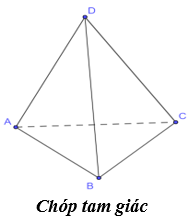
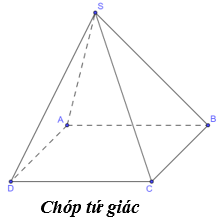
+ Đường cao của hình chóp là đường thẳng qua đỉnh và vuông góc với đáy.

+ Hình chóp có các cạnh bên bằng nhau thì chân đường cao là tâm đường tròn ngoại tiếp đa giác đáy.

+ Hình chóp có các mặt bên cùng tạo với đáy một góc bằng nhau thì chân đường cao là tâm đường tròn nội tiếp đa giác đáy

+ Hình chóp có một mặt bên vuông góc với đáy thì chân đường cao là chân đường vuông góc kẻ từ đỉnh xuống cạnh đáy của mặt bên đó.

+ 2 mặt bên cùng vuông góc với đáy thì giao tuyến của chúng vuông góc với đáy.

2. Công thức tính thể tích khối chóp

Cho khối chóp có đường cao là h

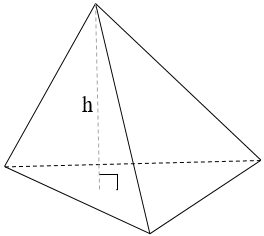
Diện tích đa giác đáy là S

3. Thể tích một số khối chóp đặc biệt

a. Khối tứ diện đều: Là khối chóp có tất cả các cạnh bằng nhau

Tất cả các mặt đều là các tam giác đều. Chân đường cao là trọng tâm của đáy

Bài toán: Cho tứ diện đều ABCD cạnh a. Tính thể tích tứ diện ABCD

Lời giải:

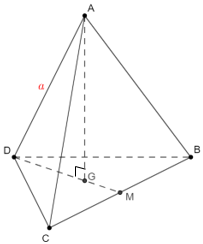
Gọi G là trọng tâm tam giác BCD. Do ABCD là tứ diện đều nên AG ⊥ (BCD) 

 .

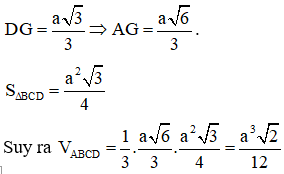b. Khối chóp tam giác đều

- Là hình chóp có tất cả các cạnh bên bằng nhau, đáy là tam giác. Chân đường cao là trọng tâm của tam giác đáy.

Bài toán 1: Cho khối chóp S.ABC đều, đáy ABC là tam giác đều cạnh a. Cạnh bên bằng a√2. Tính thể tích khối chóp.

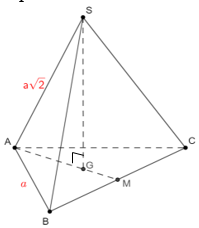
Lời giải:

Gọi G là trọng tâm tam giác ABC. Ta có SG ⊥ (ABC) 

 

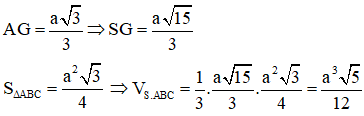
Bài toán 2: Cho khối chóp S.ABC đều có đáy ABC là tam giác vuông tại B.AB = a, BC = a√3. Các cạnh bên tạo với đáy góc 60⁰. Tính V_S.ABC.

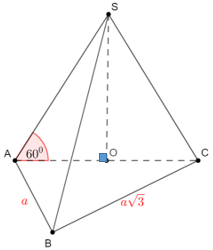
Lời giải:

Gọi O là tâm đường tròn ngoại tiếp ΔABC. Do ΔABC vuông tại B nên O là trung điểm của AC.

Ta có (SA,(ABC)) = (SA,OA) = 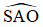= 60⁰ 

Áp dụng định lí pytago cho ΔABC ta được AC = 2a => SO = a√3 

 

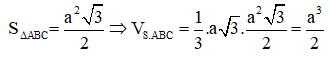
c. Khối chóp tứ giác đều

- Là hình chóp có tất cả các cạnh bên bằng nhau. Đáy là hình vuông, chân đường cao là tâm của hình vuông.

Bài toán: Cho khối chóp đều S.ABCD đáy vuông cạnh a. Các cạnh bên dài 2a. Tính thể tích khối chóp S.ABCD.

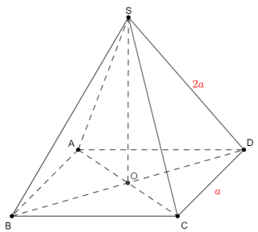
Lời giải:

Gọi O là tâm của hình vuông ABCD. Ta có SO ⊥ (ABCD) .

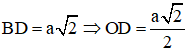. Áp dụng pytago cho ΔSOD ta được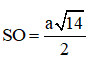  

Diện tích ABCD là a² =>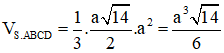  

d. Chóp tam giác có 3 cạnh bên đôi một vuông góc.

- Giả sử 3 cạnh bên có độ dài lần lượt là a, b và c. Khi đó thể tích khối chóp này là:

 

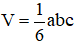
d. Khối tứ diện gần đều

- Là tứ diện có các cặp cạnh đối bằng nhau.

Bài toán: Cho tứ diện ABCD có AB = CD = a; AC = BD = b và AD = BC = c. Tính thể tích khối tứ diện ABCD.

 

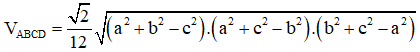
4. Công thức tỉ số thể tích

Bài toán: Cho hình chóp S.ABC. Trên các cạnh SA, SB, SC lần lượt lấy các điểm A^', B^', C^'. 

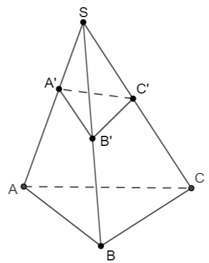
Khi đó tỉ số thể tích:

 

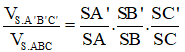
VD1. Cho hình chóp S.ABC có thể tích là 120.Trên các cạnh SA, SB, SC lần lượt lấy M, N, Q sao cho: MA = 2SM; NB = 3SN và QC = 4SQ. Tính thể tích khối chóp S.MNQ?

Lời giải:

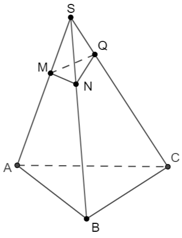
Từ giả thiết ta có: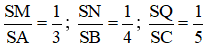

Áp dụng công thức tỉ số thể tích ta có: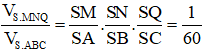  

Suy ra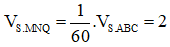  

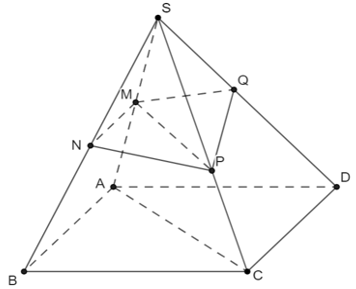
VD2. Cho hình chóp S.ABC có đáy là tam giác vuông tại B. SA ⊥ (ABC) và SA = 2a; AB = 2a; BC = a√3. Lấy M trung điểm SA và N trung điểm SB.

a. Tính thể tích khối chóp S.ABC 

b. Tính thể tích khối đa diện

Lời giải:

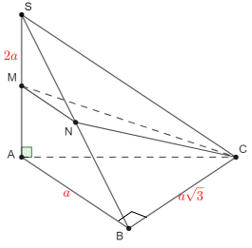
a. Diện tích ΔABC là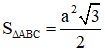  

Suy ra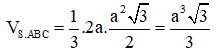  

b. Áp dụng công thức tỉ số thể tích ta có:

 

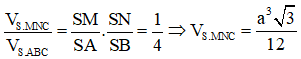
Do đó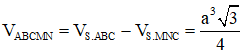  

- Chú ý: Khi áp dụng phương pháp tỉ số thể tích ta chỉ được áp dụng cho khối chóp tam giác. Nếu không là khối chóp tam giác thì ta nên chia khối chóp đã cho thành các khối chóp tam giác để có thể dùng được phương pháp thể tích.

                             

5. Luyện tập 

Dạng 1. Khối chóp có cạnh bên vuông góc với đáy

Bài 1. Cho hình chóp S.ABC đáy là tam giác vuông tại B. AC = a√2, CB = a. SA vuông góc với đáy và SA = 2a. Tính thể tích khối chóp S.ABC

Bài 2. Cho hình chóp S.ABC đáy là tam giác đều cạnh a. SA vuông góc với đáy. Góc giữa SC và đáy bằng 45⁰ . Tính thể tích khối chóp S.ABC

Bài 3. Cho hình chóp S.ABCD đáy vuông cạnh a. SA vuông góc với đáy và góc giữa (SBD) và (ABCD) bằng 60⁰ . Tính V_S.ABCD .

Bài 4. Cho hình chóp S.ABCD đáy là hình chữ nhật có AD = 2a; AB = a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Khoảng cách từ A đến mp (SCD) bằng 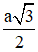. Tính thể tích khối chóp S.ABCD.

Dạng 2. Khối chóp có mặt bên vuông góc với đáy

Bài 1. Cho hình chóp S.ABCD đáy vuông cạnh a. Mặt bên SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD

Bài 2. Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết AD = a√3; CD = 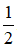AB và góc giữa SC với đáy bằng 60⁰. Tính thể tích khối chóp S.ABCD.

Dạng 3. Khối chóp có các cạnh bên bằng nhau 

Bài 1. Cho hình chóp tam giác đều S.ABC có đáy là tam giác đều cạnh a. Khoảng cách từ A đến (SBC) bằng 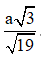. Tính thể tích khối chóp S.ABC

Bài 2. Cho hình chóp S.ABC có SA = SB = SC. Đáy ABC vuông tại B, AB = a; 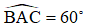. M là trung điểm SA. Khoảng cách từ M đến (SBC) bằng 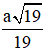. Tính thể tích khối chóp S.ABC

Dạng 4. Tỉ số thể tích

Bài 1. Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Tính thể tích của khối tứ diện AB’C’D’ biết thể tích của ABCD là 100

Bài 2. Cho hình chóp S.ABCD đáy vuông cạnh a. SA vuông góc với đáy. Góc giữa SC và đáy bằng 60⁰. Lấy A’ trên SA sao cho 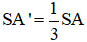. Mặt phẳng qua A’ và song song với đáy cắt các cạnh SB, SC, SD lần lượt tại B’, C’, D’. Tính thể tích khối chóp S.A’B’C’D’.

Xem thêm các Công thức Toán lớp 12 quan trọng hay khác:

• Công thức tính thể tích khối lăng trụ

• Công thức về tỉ số thể tích khối đa diện

---