Công thức giải bất phương trình lôgarit (siêu hay)
Công thức giải bất phương trình lôgarit hay nhất sẽ giúp học sinh lớp 12 nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 12.
Công thức giải bất phương trình lôgarit (siêu hay)
1. Bất phương trình lôgarit cơ bản
- Bất phương trình lôgarit cơ bản có dạng loga x > b (hoặc loga x ≥ b, loga x < b, loga x ≤ b) với a > 0, a ≠ 1.
2. Tập nghiệm của bất phương trình lôgarit cơ bản.
a. Nghiệm của bất phương trình loga x > b, (a > 0, a ≠ 1)
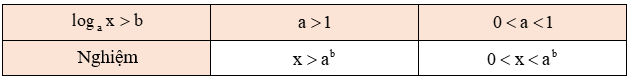
b. Tập nghiệm của bất phương trình loga x ≥ b, (a > 0, a ≠ 1)
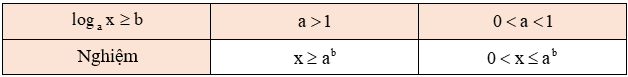
c. Tập nghiệm của bất phương trình loga x < b, (a > 0, a ≠ 1)
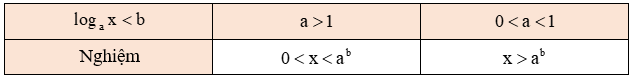
d. Tập nghiệm của bất phương trình loga x ≤ b, (a > 0, a ≠ 1)
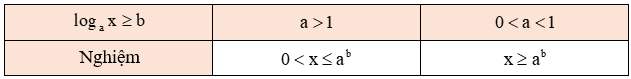
- Chú ý: Khi giải bất phương trình lôgarit ta cần tìm điều kiện của x.
3. Một số bất phương trình lôgarit đơn giản
Ví dụ 1. Giải các bất phương trình sau:
a. log0,5 (5x + 10) < log0,5 (x2 + 6x + 8)
Lời giải:
a. log0,5 (5x + 10) < log0,5 (x2 + 6x + 8)
Bất phương trình ⇔ 5x + 10 > x2 + 6x + 8 ( vì 0,5 <1)
⇔ x2 + x – 2 < 0 ⇔ -2 <x <1
Kết hợp với điều kiện ta được -2 < x < 1
Vậy bất phương trình có tập nghiệm là S = (-2;1)
⇔ x2 + 2x – 24 ⇔ -6 ≤ x ≤ 4
Kết hợp với điều kiện ta được tập nghiệm là
Ví dụ 2. Giải các bất phương trình sau:
a. log2 (x – 3) + log2 (x – 2) > 1
c. log0.2 x – log5 (x – 2) < log0.2 3
Lời giải:
a. log2 (x – 3) + log2 (x – 2) > 1
Điều kiện: x > 3
Bất phương trình ⇔ log2 [(x – 3)(x – 2)] > 1
⇔ log2 (x2 – 5x + 6) > 1
Kết hợp với điều kiện ta được tập nghiệm là S = (4;+ ∞)
Điều kiện: x > 3
Bất phương trình ⇔ 2log3 (x – 3) – log3 (x2 -2x + 3) ≤ 1
⇔ x2 – 6x + 9 ≤ 3x2 – 6x + 9 ⇔ x2 ≥ 0 ∀ x
Kết hợp với điều kiện ta được tập nghiệm là S = (3;+ ∞)
c. log0.2 x – log5 (x – 2) < log0.2 3
Điều kiện: x > 2
Bất phương trình ⇔ log0.2 x – log0.2 3 < log5 (x-2)
Kết hợp với điều kiện ta được tập nghiệm là S = (3;+ ∞)
Ví dụ 3. Giải các bất phương trình sau:
Lời giải:
Điều kiện X > 0
Đặt t = log3 x. Bất phương trình trở thành:
t2 – 5t + 6 ≤ 0 ⇔2 ≤ t ≤ 3
Với 2 ≤ t ≤ 3 ⇒ 2 ≤ log3 x ≤ 3 ⇔ 9 ≤ x ≤ 27
Kết hợp với điều kiện ta được tập nghiệm là S = [9;27]
Điều kiện: x > 0; log x ≠ {-1;5}
Đặt t = log x, t ≠ {-1;5}. Bất phương trình trở thành:
t2 – 5t + 6 ⇔ t = 2; t = 3
-t2 + 4t + 5 = 0 ⇔ t = -1; t = 5
Bảng xét dấu:
Với t ∈ (2;3) ⇒ 2 < log x <3 ⇔ 100 < x < 1000
Với t ∈ (5;+∞) ⇒ log x > 5 ⇔ x > 105
Vậy bất phương trình có tập nghiệm là
Ví dụ 4. Giải bất phương trình:
Lời giải:
4. Luyện tập giải bất phương trình lôgarit
Bài 1. Giải các bất phương trình sau:
a. log8 (4 – 2x) ≥ 2
c. log2 (x2 – 2x) > 3
Bài 2. Giải các bất phương trình sau:
Bài 3. Giải các bất phương trình sau:
Bài 4. Giải các bất phương trình sau:
b. log2 x ≤ 6 -x
Xem thêm các Công thức Toán lớp 12 quan trọng hay khác:
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)


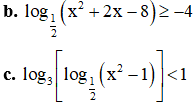
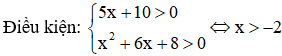
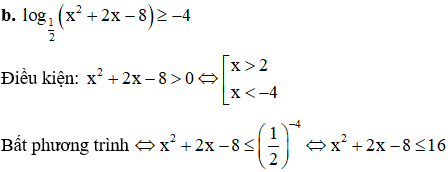
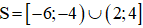

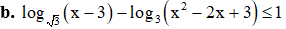
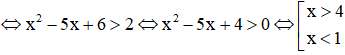
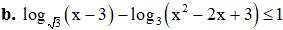
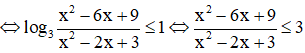
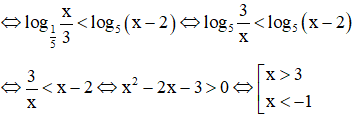
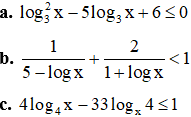
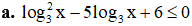
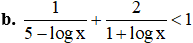
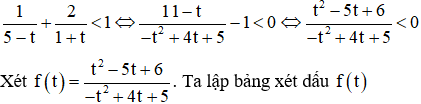
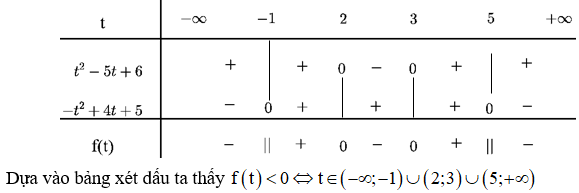
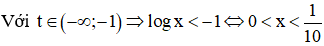
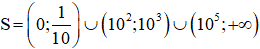
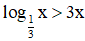

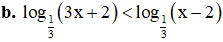
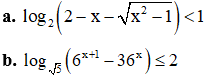
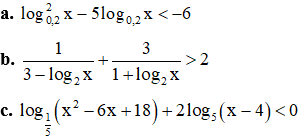
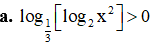



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

