Công thức tính thể tích các khối tròn xoay đặc biệt (siêu hay)

Công thức tính thể tích các khối tròn xoay đặc biệt (siêu hay)

Công thức tính thể tích các khối tròn xoay đặc biệt hay nhất sẽ giúp học sinh lớp 12 nắm vững công thức, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi Toán 12.

1. Khối chỏm cầu

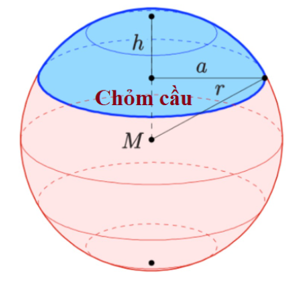
Chỏm cầu thu được khi ta dùng một mặt phẳng (P) cắt mặt cầu

Là phần màu xanh trong hình vẽ

- Các đại lượng:

+ Phần mặt cầu bị cắt là mặt đáy chỏm cầu có dạng hình tròn và bán kính là a

+ Khoảng cách từ mặt đáy tới đỉnh của chỏm là chiều cao h

- Công thức tính diện tích xung quanh

S_xq=2πrh

Hoặc

S_xq =π(a² +h²) 

Trong đó: r là bán kính mặt cầu ; h là chiều cao của chỏm và a là bán kính đáy chỏm.

- Công thức tính thể tích chỏm cầu

V= πh².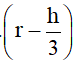

Hoặc     

V= 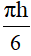(3a² +h²)

2. Khối tròn xoay dạng đặc biệt

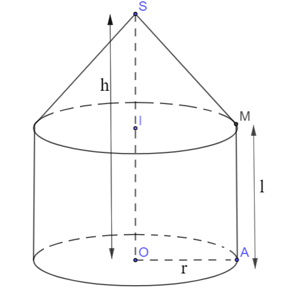
- Được tạo thành khi quay đường gấp khúc SMA quanh trục SO.

- Về mặt hình dạng: Gồm 2 phần

+ Hình nón bên trên

+ Hình trụ bên dưới

- Các đại lượng

+ Chiều cao SO (h)

+ Chiều cao hình trụ OI (l)

+ Bán kính đáy (r)

- Công thức tính diện tích xung quanh: Là tổng diện tích 2 phần

S_xq= 2πrl+πr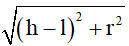

- Công thức tính thể tích: Là tổng thể tích 2 phần

V=πr²l+ 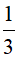πr²(h-1)

3. Ví dụ áp dụng

Ví dụ 1. Tính diện tích xung quanh và thể tích chỏm cầu trong các trường hợp

a. r=5cm; h=10cm

b. a=4dm; h=6dm

Lời giải:

a. Diện tích xung quanh chỏm cầu là:

S_xq=2πrh=2π.5.10=100π

Thể tích khối chỏm là:

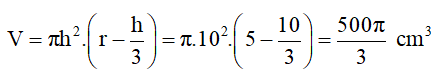
b. Diện tích xung quanh chỏm cầu là:

S_xq=π(a²+h²) =π(4² +6²) =52π dm²

Thể tích chỏm cầu là:

V= 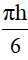(3a²+h²)= 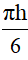(3.4²+6²) =84π dm³

Ví dụ 2. Một gia đình có bồn tắm có bề mặt phẳng và lòng trong như hình vẽ dưới. Lòng trong của bồn tắm có hình dạng bán cầu, mất đi chỏm cầu. với r là bán kính khối cầu, h là chiều cao của chỏm cầu và 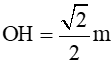. Thể tích (m³)  lòng trong của bồn tắm là

Lời giải:

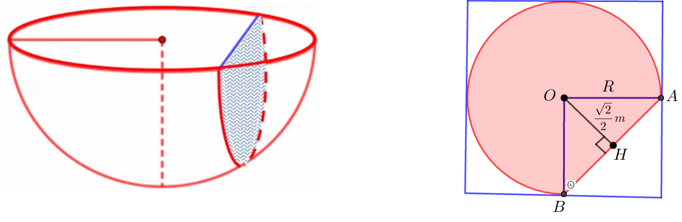
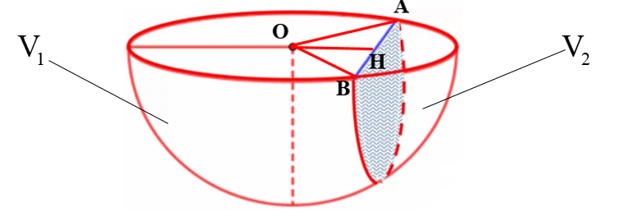
Gọi V là thể tích lòng trong của bồn tắm cần tính

V₁ là thể tích của nửa quả cầu bán kính r

V₂ là thể tích của nửa khối chỏm cầu như hình vẽ

=> V= V₁- V₂

Xét tam giác OAB vuông cân tại O đường cao OH= 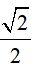  => r=OA=l

=> Chiều cao chỏm cầu là: h=r -OH =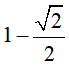 

Khi đó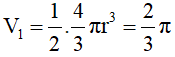

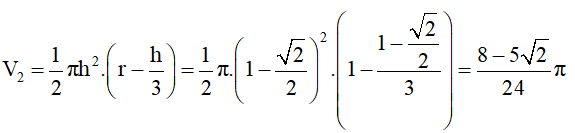
=> V= V₁ - V₂ =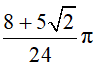 

Ví dụ 3. Một chiếc bút chì được thiết kế phần thân bút là hình trụ và đầu bút là hình nón như hình vẽ 

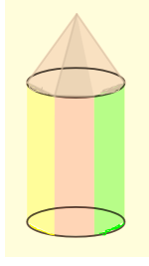
Biết rằng chiều dài của bút là 12cm; đường kính đáy bằng 2cm và phần thân bút dài 10cm. Tính thể tích của chiếc bút.

Lời giải:

Chiều cao của phần nón là: 12-10=2 cm

Bán kính đáy là r=1 cm

 Thể tích nón là V₁= 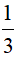πl².2 =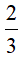πcm³

Thể tích của khối trụ là V₂= π,l².10=10π cm³

Do đó thể tích của bút là V=V₁ + V₂ = 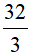cm³

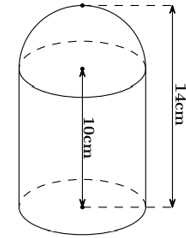
Ví dụ 4. Một công ty sản xuất cốc đựng trà sữa có dạng phần thân là hình trụ và nắp đậy là chỏm cầu. Biết phần thân có bán kính đáy bằng 3cm, phần nắp đậy được tính riêng (hình vẽ minh họa). Chi phí sản xuất cốc là bao nhiêu biết phần thân có giá 1000 đ/dm² và phần nắp có giá 1500 đ/dm².

Lời giải:

Gọi S là diện tích của cốc đựng trà sữa

S₁ là diện tích phần thân hình trụ bán kính r=3cm ; chiều cao h=10cm

=> S₁ = 2π.3.10 =60π cm² = 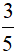πdm²

=> Chi phí sản xuất là: 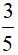π.1000 ≈ 1885 đồng

S₂ là diện tích phần chỏm cầu bán kính a=3cm ; chiều cao h=4cm

=> S₂=π(3² + 4² ) = 25π cm² = 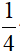πdm²

=> Chi phí sản xuất là: 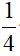π.1500  ≈ 1178đồng

Vậy tổng chi phí là khoảng 3600 đồng.

Xem thêm các Công thức Toán lớp 12 quan trọng hay khác:

• Công thức tính bán kính của hình nón

• Công thức tính đường sinh của hình nón

• Công thức tính diện tích hình nón

• Công thức tính thể tích khối nón

• Công thức tính bán kính hình trụ

---