Tổng hợp Công thức Hàm số lũy thừa. Hàm số mũ và hàm số logarit (quan trọng)
Trọn bộ công thức Hàm số lũy thừa. Hàm số mũ và hàm số logarit quan trọng với lý thuyết và bài tập tự luyện giúp học sinh vận dụng và làm bài tập thật tốt môn Toán.
Tổng hợp Công thức Hàm số lũy thừa. Hàm số mũ và hàm số logarit (quan trọng)
Công thức lũy thừa
1. Lí thuyết
a. Lũy thừa với số mũ nguyên
- Lũy thừa với số mũ nguyên dương
Cho a ∈ R, n ∈ N*. Khi đó:
- Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0
Cho a ≠ 0. Khi đó:
Ví dụ:
- Chú ý: Lũy thừa với số mũ nguyên có các tính chất tương tự tính chất của lũy thừa với số mũ nguyên dương.
+ 00 và 0-n không có nghĩa.
b. Căn bậc n
- Cho số thực b và số nguyên dương n ≥ 2.
Số a được gọi là căn bậc n của số b nếu an = b
Ví dụ: 4 là căn bậc ba của 64 vì 43 = 64
c. Lũy thừa với số mũ hữu tỉ
- Cho số thực a > 0 và số hữu tỉ 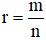
Khi đó:
d. Lũy thừa với số mũ vô tỉ
- Giả sử a là một số dương, α là một số vô tỉ, (rn) là một dãy số hữu tỉ sao cho
2. Các tính chất của lũy thừa
Cho 2 số dương a, b; m,n ∈ R. Khi đó:
+) am.an = am+n
+)
+) (a.b)m = am.bm
+)
+) (am)n = am.n
- Nếu a > 1 thì am > an ⇔ m > n
- Nếu 0 < a < 10 thì am > an ⇔ m < n
3. Ví dụ
Ví dụ1. Cho a, b là các số dương. Hãy viết rút gọn các biểu thức sau dưới dạng lũy thừa:
Lời giải:
Ví dụ2. Tìm x biết:
a. x8 – 15x4 – 16 = 0
b. x6 + 6x3 – 16 = 0
Lời giải:
a. Đặt t = x4, (t ≥ 0). Phương trình trở thành:
Vậy x = -2; x = 2
b. Đặt t = x3. Phương trình trở thành:
....................................
....................................
....................................
Công thức logarit
1. Lí thuyết
a. Định nghĩa: Cho 2 số dương a, b với a ≠ 1. Số x thỏa mãn đẳng thức ax = b được gọi là lôgarit cơ số a của b và kí hiệu là logab
ax = b ⇔ x = loga b
b. Các tính chất: Với a,b > 0; a ≠ 1 ta có
2. Các quy tắc tính
a. Lôgarit của một tích
- Định lí 1: Với các số dương a, x, y và a ≠ 1 ta có:
loga(x.y) = logax + logay
- Chú ý: Định lí 1 có thể mở rộng cho tích của n số dương:
b. Lôgarit của một thương
- Định lí 2: Với các số dương a, x, y và a ≠ 1 ta có:
c. Lôgarit của một lũy thừa
- Định lí 3: Lôgarit của một lũy thừa bằng tích của số mũ với lôgarit của cơ số.
logabα = α.logab (a,b > 0; a ≠ 1; α ∈ R)
- Đặc biệt:
3. Công thức đổi cơ số, lôgarit thập phân và lôgarit tự nhiên.
- Định lí 4: Cho 3 số dương a, b, c với a ≠ 1, c ≠ 1 ta có:
- Đặc biệt:
- Lôgarit thập phân: Là lôgarit cơ số 10. Kí hiệu: log10 x = log x
- Lôgarit tự nhiên: Là lôgarit cơ số e. Kí hiệu: loge x = ln x
- Chú ý: Tìm số các chữ số của một lũy thừa:
Bài toán: Số aα có bao nhiêu chữ số?
Số các chữ số của aα chính là [log aα] + 1 (phần nguyên aα cộng 1)
- Ví dụ: Số 320 có [log 320] + 1 = 10 chữ số.
4. Các ví dụ
Ví dụ1. Tìm x biết
a. log2 x = 3
b. 3x = 4
c. log3 x = 4log3 a + 7log3 b (a,b > 0)
Lời giải:
a. log2 x = 3 ⇔ x = 23 ⇔ x = 8
b. 3x = 4 ⇔ x = log3 4 ⇔ x = 2
c. log3 x = 5log3 a + 7log3 b ⇔ log3 x = log3 a4 + log3 b7
⇔ log3 x = log3(a4.b7) ⇔ x = a4.b4
....................................
....................................
....................................
Trên đây tóm tắt một số nội dung trong trọn bộ công thức Toán lớp 12 Chương, để xem đầy đủ mời quí bạn đọc vào từng bài ở trên!
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

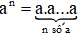
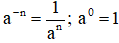
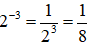

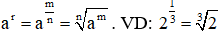
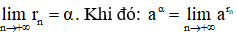
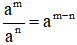
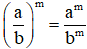
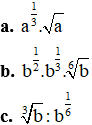
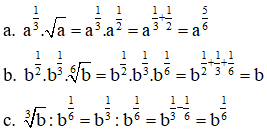
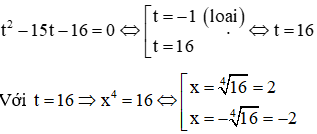
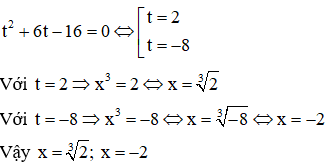

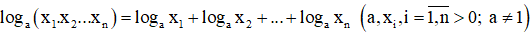
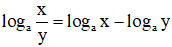
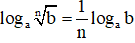
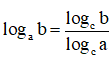
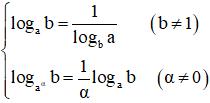



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

