Trọn bộ Công thức Toán lớp 8 Chương 1: Phép nhân và phép chia các đa thức quan trọng

Trọn bộ Công thức Toán lớp 8 Chương 1: Phép nhân và phép chia các đa thức quan trọng

Nhằm mục đích giúp học sinh dễ dàng nhớ và nắm vững các công thức Toán 8, VietJack biên soạn tài liệu trọn bộ công thức Toán lớp 8 Đại số Chương 1: Phép nhân và phép chia các đa thức đầy đủ công thức quan trọng, lý thuyết và bài tập tự luyện giúp học sinh vận dụng để biết cách làm bài tập Toán 8.

• Công thức nhân đơn thức, đa thức với đa thức
• Bảy hằng đẳng thức đáng nhớ
• Hằng đẳng thức số 1
• Hằng đẳng thức số 2
• Hằng đẳng thức số 3
• Hằng đẳng thức số 4
• Hằng đẳng thức số 5
• Hằng đẳng thức số 6
• Hằng đẳng thức số 7
• Hằng đẳng thức mở rộng
• Phương pháp phân tích đa thức thành nhân tử
• Phương pháp chia đơn thức, đa thức cho đơn thức
• Chia đa thức cho đa thức một biến đã sắp xếp

---

---

---

Công thức nhân đơn thức đa thức với đa thức

I. Lý thuyết

1. Công thức nhân đơn thức với đa thức.

A ( B + C ) = A.B + A.C

A ( B + C +  D ) = A.B + A.C + A.D

Với A, B, C, D là các đơn thức.

Giải thích: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức rồi cộng các tích lại với nhau.

Ví dụ: 

a) 2x ( 4x³ - x + 1)

= 2x.4x³ - 2x.x + 2x.1

= 2.4.x.x³ - 2x² + 2x

= 8x⁴ - 2x² + 2x 

b) 6x² ( 4x⁵ - 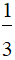x + 1 )

= 6x².4x⁵ - 6x². 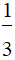x + 6x².1

= 6.4.x².x⁵ - 6.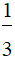 .x².x + 6x²

= 24x⁷ - 2x³ + 6x²

2. Công thức nhân đa thức với đa thức

( A + B )( C + D ) = A( C + D ) + B( C + D )

= A.C + A.D + B.C + B.D

Giải thích: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa đa thức thứ nhất với từng hạng tử của đa thức thứ hai rồi cộng các tích lại với nhau.

Chú ý: Ta cần sử dụng các công thức lũy thừa cơ bản để đưa các đơn thức, đa thức về dạng thu gọn.

* Công thức lũy thừa:

 a,b ∈ Ζ; m,n ∈ N

a^m.aⁿ = a^m+n 

a^m : aⁿ = a^m-n ( a ≠ 0, m ≥ n )

(ab)^m = a^mbⁿ

(a^m)ⁿ = a^m.n

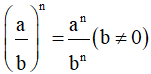
a⁰ = 1

a¹ = a

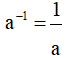
 Ví dụ:

a) ( x + 1 )( x – 2 )

= x ( x -2 ) + 1.( x - 2 )

= x.x - x.2 + 1.x - 1.2

= x² - 2x + x -2 

= x² + ( -2x + x ) -2

= x² - x - 2

 b) ( x - 2 )( x² - 2x )

= x ( x² - 2x ) - 2( x² - 2x ) 

= ( x. x² - x.2x ) - ( 2x² - 2.2x )

= ( x³ - 2x² ) - ( 2x² - 4x )

= x³ - 2x² - 2x² + 4x

= x³ + ( -2x² - 2x² ) + 4x

= x³ - 4x² + 4x

II. Bài tập:

Thực hiện phép nhân:

a) - 2x²( 2x² - 3x -  )

b) 3xy( x³ + y )

c) 4xy² ( x + x³ - 3y) 

d) 5xy ( x² + 3xy + y³) 

e) ( 2xy + 1 )( 2x + 3y ) 

f) ( xy + x + 3 )( x - 3y + 1 )  

g) ( 2x²y - 1 )( 2x + 3y)(x - 2) 

h) ( 2y - x )( 2xy + 3x + y)

i) ( 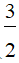x²y² - x - y)(2x + 3y)  

Bảy hằng đẳng thức đáng nhớ

I. Lý thuyết 

          1. ( a + b )² = a² + 2ab + b²

          2. ( a - b )² = a² - 2ab + b²  

          3. a² - b² = ( a - b )( a + b )

          4. ( a + b )³ = a³ + 3a²b + 3ab² + b³

          5. ( a - b )³ = a³ - 3a²b + 3ab² - b³

          6. a³ + b³ = ( a + b )( a² - ab + b² )

          7. a³ - b³ = ( a - b )( a² + ab + b² )  

1. Bình phương một tổng

Với hai số bất kỳ ta luôn có: Bình phương một tổng sẽ bằng bình phương số thứ nhất cộng với hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương số thứ hai.

( a + b )² = a² + 2ab + b²  

Ví dụ: Khai triển các biểu thức sau theo hằng đẳng thức:

a) ( x + 2 )²                                          

b) ( 2x + 1 )²

Hướng dẫn:

a) ( x + 2 )² = x² + 2.x.2 + 2² = x² + 4x + 4 

b) ( 2x + 1 )² = ( 2x )² + 2.2x.1 + 1² = 4x² + 4x + 1

2. Bình phương một hiệu.

Với hai số bất kỳ ta luôn có: Bình phương một hiệu sẽ bằng bình phương số thứ nhất trừ đi hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương số thứ hai.

 ( a - b )² = a² - 2ab + b²  

Ví dụ: Khai triển các biểu thức sau theo hằng đẳng thức: 

a) ( x - 3 )²                                          b) ( 2x - 1 )²  

Hướng dẫn:

a) ( x - 3 )² = x² - 2.x.3 + 3² = x² - 6x + 9 

b) ( 2x - 1 )² = ( 2x )² - 2.2x.1 + 1² = 4x² - 4x + 1 

3. Hiệu hai bình phương.

Với hai số bất kỳ ta luôn có hiệu hai bình phương bằng tổng của hai số nhân với hiệu của hai số.

  a² - b² = ( a - b )( a + b ) 

Ví dụ: Khai triển các biểu thức sau theo hằng đẳng thức: 

a) x² - 16                                    b) x² - 4y² 

Hướng dẫn:

a) x² - 16 = x² - 4² = ( x - 4 )( x + 4 ) 

b) x² - 4y² = x² - ( 2y )² = ( x - 2y )( x + 2y )

4. Lập phương một tổng.

Lập phương một tổng của hai số bất kỳ sẽ bằng lập phương số thứ nhất cộng với ba lần bình phương số thứ nhất nhân số thứ hai, cộng với ba lần bình phương số thứ hai nhân số thứ nhất sau đó cộng với lập phương số thứ ba.

 ( a + b )³ = a³ + 3a²b + 3ab² + b³ 

Ví dụ: Khai triển biểu thức sau theo hằng đẳng thức: ( x + 2y )³    

Hướng dẫn:

 ( x + 2y )³ = x³ + 3.x².2y + 3.x.( 2y )² + ( 2y )³ 

 = x³ + 6x²y + 12xy² + 8y³

5. Lập phương một hiệu.

Lập phương một hiệu của hai số bất kỳ sẽ bằng lập phương số thứ nhất trừ đi ba lần bình phương số thứ nhất nhân số thứ hai, cộng với ba lần bình phương số thứ hai nhân số thứ nhất sau đó trừ đi lập phương số thứ 3.

 ( a - b )³ = a³ - 3a²b + 3ab² - b³ 

Ví dụ: Khai triển biểu thức sau theo hằng đẳng thức: ( x - 2y )³

Hướng dẫn:

 ( x - 2y )³ =  x³ - 3.x².2y + 3.x.( 2y )² - ( 2y )³ 

 = x³ - 6x²y + 12xy² - 8y³

 6. Tổng hai lập phương.

Tổng của hai lập phương của hai số bất kỳ sẽ bằng tổng của hai số sau đó nhân với bình phương thiếu của hiệu số thứ nhất và số thứ hai.

          a³ + b³ = ( a + b )( a² - ab + b² )

Ví dụ: Khai triển biểu thức sau theo hằng đẳng thức: x³ + 8

Hướng dẫn: 

 x³ + 8 = x³ + 2³ = ( x + 2 )(x² - x.2 + 2² ) = ( x + 2 )( x² - 2x + 4 ) 

7. Hiệu hai lập phương

Hiệu của hai lập phương của hai số bất kỳ sẽ bằng số thứ nhất trừ đi số thứ hai sau đó nhân với bình phương thiếu của tổng số thứ nhất và số thứ hai.

 a³ - b³ = ( a - b )( a² + ab + b² )  

Ví dụ: Khai triển biểu thức sau theo hằng đẳng thức: x³ - 27  

Hướng dẫn: 

 x³ - 27 = x³ - 3³ = ( x - 3 )(x² + x.3 + 3² ) = ( x - 3 )(x² + 3x + 9 )

II. Bài tập tự luyện

Ví dụ: Khai triển các hằng đẳng thức sau:

a) ( 2x + 3 ) 

b) ( 3x - 2 )² 

c) ( x + 4 )³ 

d) 4x² - 16 

e) x³ + 125 

f) 27x³ -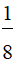 

g) x² - 16y² 

h) ( x + 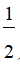)² 

i) ( 2x + 3y )² 

j) ( x - 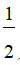y)²

k) ( 3x - y )³  

..........................

..........................

..........................

Trên đây là tóm lược một số nội dung có trong tổng hợp công thức Toán lớp 8 Chương 1 Đại số, mời quí bạn đọc vào từng bài để xem đầy đủ, chi tiết!

---