Công thức Toán 8 Chương 1: Tứ giác quan trọng

Công thức Toán 8 Chương 1: Tứ giác quan trọng

Nhằm mục đích giúp học sinh dễ dàng nhớ và nắm vững các công thức Toán 8, VietJack biên soạn tài liệu trọn bộ công thức Toán lớp 8 Hình học Chương 1: Tứ giác đầy đủ công thức quan trọng, lý thuyết và bài tập tự luyện giúp học sinh vận dụng và làm bài tập thật tốt môn Toán lớp 8.

• Công thức Tứ giác

• Công thức Đường trung bình của tam giác, của hình thang

• Công thức Hình thang

• Công thức Hình bình hành

• Công thức Đối xứng trục

• Công thức Hình chữ nhật

• Công thức Đối xứng tâm

• Công thức Hình thoi

• Công thức Hình vuông

---

---

---

Công thức Tứ giác

I. Lý thuyết

1. Khái niệm

Tứ giác là một đa giác gồm 4 cạnh và 4 đỉnh, trong đó không có bất kỳ 2 đoạn thẳng nào cùng nằm trên một đường thẳng.

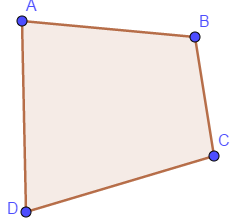
2. Tứ giác lồi

- Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng với bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác đó.

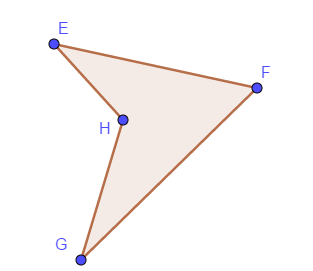
- Trái ngược với tứ giác lồi là tứ giác lõm

Tứ giác ABCD là tứ giác lồi.

Tứ giác EFGH là tứ giác lõm.

Chú ý khi làm bài tập ta chỉ quan tâm đến tứ giác lồi, vì vậy nếu đề bài chỉ nói là tứ giác thì ta hiểu đấy là tứ giác lồi

Xét tứ giác 

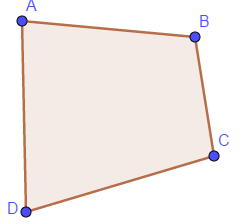
Khi ta đọc tên tứ giác ta chỉ đọc theo một chiều:

Ví dụ: 

Cách đọc đúng là: ABCD; BADC;...

Cách đọc sai là: ACBD; BCAD;...

Công thức Đường trung bình của tam giác, của hình thang

I. Lý thuyết

1. Đường trung bình của tam giác

a) Định nghĩa:

Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh tam giác đó.

b) Định lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

c) Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh thứ ba.

Xét hình vẽ:

 

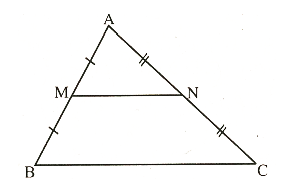
Tam giác ABC có:

M là trung điểm AB

N là trung điểm AC

Nên MN là đường trung bình của tam giác ABC

 

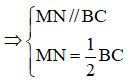
2. Đường trung bình của hình thang.

a) Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh bên hình thang.

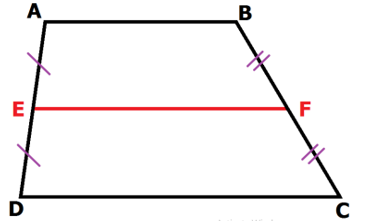
ABCD là hình thang, AB // CD

E là trung điểm AD, F là trung điểm BC

EF là đường trung bình của hình thang ABCD.

b) Định lí 2: Đường thẳng đi qua trung điểm của cạnh bên thứ nhất và song song với cạnh đáy thì nó đi qua trung điểm của cạnh bên thứ hai của hình thang.

c) Định lí 3: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Xét hình thang ABCD có đường trung bình là FE

 

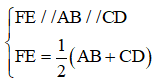
II. Bài tập

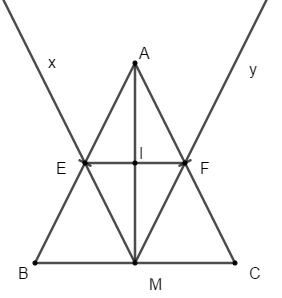
Bài 1: Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E, kẻ tia My song song với AB và cắt AC tại F. Chứng minh:

a) EF là đường trung bình của tam giác ABC.

b) AM là đường trung trực của EF

Lời giải:

a)

+ Vì Mx // AC, Mx qua trung điểm M của BC nên Mx đi qua trung điểm của AB

Mà Mx cắt AB tại E nên E là trung điểm của AB (1)

+ Vì My // AB, My đi qua trung điểm M của BC nên My đi qua trung điểm của AC.

Mà My cắt AC tại F nên F là trung điểm của AC (2)

Từ (1) và (2)  EF là đường trung bình của tam giác ABC

b) Vì ABC là tam giác cân tại A nên AM là đường trung tuyến đồng thời cũng là đường cao

=> AM ⊥ BC 

Vì EF là đường trung bình của tam giác ABC

=> EF // BC
 mà AM ⊥ BC

=> EF ⊥  AM (3)

Gọi I là giao điểm của EF và AM

Vì MF // AB, M là trung điểm của BC nên MF là đường trung bình của tam giác ABC 

 

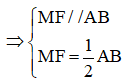
Ta có: MF // AB => MF // AE

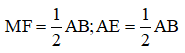nên MF = AE

Lại có: MF // AE 

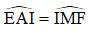(hai góc so le trong)

Xét tam giác IEA và tam giác IFM có

 

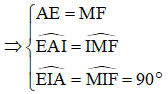
 => ΔIEA = ΔIFM (cạnh huyền – góc nhọn) 

=> IE = IF (4)

Từ (3) và (4) => AM là đường trung trực của EF.

..........................

..........................

..........................

Trên đây là tóm lược một số nội dung có trong tổng hợp công thức Toán lớp 8 Chương 1: Tứ giác, mời quí bạn đọc vào từng bài để xem đầy đủ, chi tiết!

---