Công thức tính diện tích hình bình hành đầy đủ (có giải chi tiết)

---

---

Công thức tính diện tích hình bình hành (siêu hay)

Bài viết Công thức tính diện tích hình bình hành hay, chi tiết Toán 8 hay nhất gồm 2 phần: Lý thuyết và Các ví dụ áp dụng công thức trong bài có lời giải chi tiết giúp học sinh dễ học, dễ nhớ Công thức tính diện tích hình bình hành hay, chi tiết.

I. Lí thuyết

Diện tích hình bình hành bằng tích của một cạnh nhân với chiều cao ứng với cạnh đó

S = a.h   với a là độ dài cạnh đáy, h là độ dài chiều cao tương ứng.

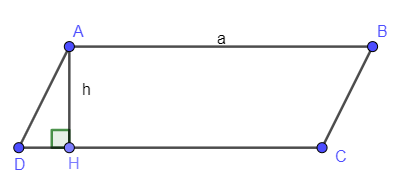
Cho hình bình hành ABCD có CD = AB = a, đường cao AH = h. Diện tích hình bình hành là:

 $S_{ABCD}=CD.AH=a.h$ (đơn vị diện tích)

II. Các ví dụ:

Ví dụ 1: Tính số đo góc $\widehat{D}$ của hình bình hành ABCD có diện tích là $30c{m}^2$, AB = 10cm, AD = 6cm, $\widehat{A}>\widehat{D}$.

Lời giải:

Kẻ AH là đường cao của hình bình hành, AH vuông góc với CD tại H.

Vì ABCD là hình bình hành nên AB = CD = 10cm; BC = AD = 6cm.

Ta có:

$$\begin{gathered} S_{ABCD}=AH.CD \\ \iff 30=AH.10 \end{gathered}$$

$\iff AH=3cm$ (1)

Gọi E là trung điểm của AD nên EA = ED = 3cm  (2)

Xét tam giác AHD vuông tại H, có E là trung điểm của AD nên HE là đường trung tuyến ứng với cạnh huyền.

 $\Rightarrow HE=\frac{1}{2}AD=\frac{1}{2}.6=3cm$ (3)

Từ (1); (2); (3) $\Rightarrow HE=AH=AE=3cm$

$\Rightarrow$ Tam giác AHE là tam giác đều

$\Rightarrow \widehat{EAH}={60}^{\circ }\Rightarrow \widehat{DAH}={60}^{\circ }$

Xét tam giác AHD có:

$\widehat{DAH}+\widehat{DHA}+\widehat{ADH}={180}^{\circ }$(định lý tổng ba góc trong một tam giác).

$$\begin{gathered} \iff {60}^{\circ }+{90}^{\circ }+\widehat{ADH}={180}^{\circ } \\ \Rightarrow \widehat{ADH}={180}^{\circ }-{90}^{\circ }-{60}^{\circ } \\ \iff \widehat{ADH}={30}^{\circ } \end{gathered}$$

Vậy $\widehat{D}={30}^{\circ }$.

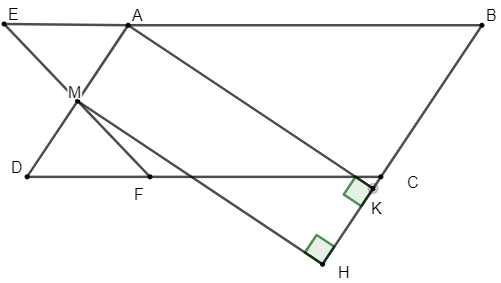
Ví dụ 2: Cho hình bình hành ABCD, M là trung điểm của AD, qua M kẻ đường thẳng d cắt AB, CD lần lượt tại E và F. Kẻ MH vuông góc với BC tại H.

Chứng minh: $S_{EBCF}=MH.BC$.

Lời giải:

Vì ABCD là hình bình hành nên AB // CD mà E thuộc AB, F thuộc CD nên AE // DF

$\Rightarrow \widehat{EAM}=\widehat{MDF}$ (hai góc so le trong)

Vì M là trung điểm của AD nên AM = MD
Xét tam giác AEM và tam giác DFM có:

$\widehat{EAM}=\widehat{MDF}$ (chứng minh trên)

AM = DM (chứng minh trên)

$\widehat{EMA}=\widehat{FMD}$ (hai góc đối đỉnh)

Do đó: $\mathrm{\Delta }AEM=\mathrm{\Delta }DFM$ (g – c - g)

  $\Rightarrow S_{AEM}=S_{DFM}$ (1)

Ta có:

 $S_{EBCF}=S_{AEM}+S_{MABCF}$ (2)

  $S_{ABCD}=S_{DFM}+S_{MABCF}$ (3)

Từ (1); (2); (3)   $\Rightarrow S_{EBCF}=S_{ABCD}$  (4)

Kẻ AK vuông góc với BC tại K

Vì AK vuông góc với BC nên AK là đường cao của hình bình hành ABCD.

Lại có AK vuông góc với BC; MH vuông góc với BC nên MH // AK

Xét tứ giác AKHM có:

AK // MH (chứng minh trên)

AM //HK (do ABCD là hình bình hành)

Do đó tứ giác AKHM là hình bình hành

$\Rightarrow AK=MH$

Ta có:

$S_{ABCD}=AK.BC$(mà AK = MH)

 $\Rightarrow S_{ABCD}=MH.BC$ (5)

Từ (4) và (5) $\Rightarrow S_{EBCF}=MH.BC$ (điều phải chứng minh).

Xem thêm các Công thức Toán lớp 8 quan trọng hay khác:

• Công thức diện tích hình thoi hay, chi tiết

• Công thức tính diện tích tứ giác có hai đường chéo vuông góc hay, chi tiết

• Công thức tính diện tích đa giác hay, chi tiết

• Hai phân thức bằng nhau hay, chi tiết

• Tính chất cơ bản của phân thức hay, chi tiết

---

---

---