3+ Đề thi khảo sát chất lượng đầu năm Toán 12 năm 2025 (có lời giải)

Tuyển chọn Đề thi khảo sát chất lượng đầu năm Toán 12 năm 2025 chọn lọc, có lời giải dùng chung cho sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều được các Giáo viên nhiều năm kinh nghiệm biên soạn và sưu tầm từ đề thi KSCL đầu năm Toán 12 của các trường THPT. Hi vọng bộ đề thi này sẽ giúp học sinh ôn tập và đạt kết quả cao trong các bài thi khảo sát chất lượng đầu năm môn Toán 12.

3+ Đề thi khảo sát chất lượng đầu năm Toán 12 năm 2025 (có lời giải)

Xem thử

Chỉ từ 60k mua trọn bộ đề khảo sát chất lượng đầu năm Toán 12 theo cấu trúc mới bản word có lời giải chi tiết, trình bày đẹp mắt, dễ dàng chỉnh sửa:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Phòng Giáo dục và Đào tạo .....

Đề thi khảo sát chất lượng đầu năm

Năm 2025

Bài thi môn: Toán 12

Thời gian làm bài: 90 phút

(Đề số 1)

 PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1. Cho cấp số cộng có số hạng đầu u₁ = 2, công sai d = -4. Số hạng thứ năm của cấp số cộng là

A. 512

B. -14

C. -512

D. -18

Câu 2. Thống kê số phút học bài ở nhà mỗi ngày của 100 học sinh ta có bảng phân bố tần số ghép nhóm như sau

Số phút	[30; 60)	[60; 90)	[90; 120)	[120; 150)
Số học sinh	18	15	42	25

Số học sinh có thời gian học ít hơn 2 tiếng trong số học sinh trên là

A. 15

B. 33

C. 75

D. 18 . 

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; -1). Tọa độ hình chiếu vuông góc của A trên mặt phẳng (Oyz) là 

A. (0; 2; -1) .

B. (1; 0; 0).

C. (1; 2; 0) .

D. (1; 0; -1)

Câu 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x⁴ - 2x² - 1 trên đoạn [-1 ; 2]. Giá trị của biểu thức M + 2m bằng

A. 3.

B. 5.

C. 6.

D. 4.

Câu 5. Cho khối lăng trụ đều có diện tích đáy bằng 2 (m²) và chiều cao bằng 3 (m). Thể tích khối lăng trụ đã cho bằng

A. $\frac{3\sqrt{3}}{2}\left({\text{m}}^3\right)$.

B. 2 (m³).

C. $\frac{\sqrt{3}}{2}\left({\text{m}}^3\right)$.

D. 6 (m³)

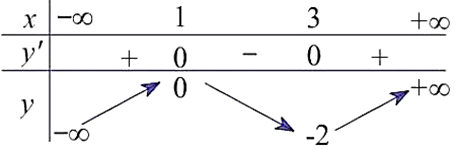
Câu 6. Cho hàm số f(x) liên tục trên ℝ và có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng

A. (-2; 0).

B. (-∞; 0).

C. (3; +∞).

D. (1; 3).

Câu 7. Đường tiệm cận xiên của đồ thị hàm số $y=2x-1+\frac{1}{x}$ có phương trình là:

A. y = 1 - 2x.

B. y = 2x.

C. y = 2x - 1.

D. y = -2x.

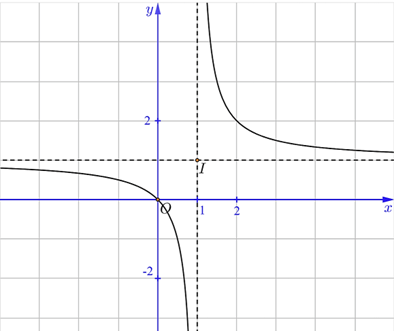
Câu 8. Hàm số nào dưới đây có đồ thị như hình vẽ sau?

A. $y=\frac{x}{x+1}$.

B. $y=-\frac{x}{x-1}$.

C. $y=-\frac{x}{x+1}$.

D. $y=\frac{x}{x-1}$.

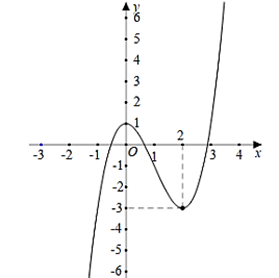
Câu 9. Cho hàm số bậc ba  có đồ thị như hình vẽ dưới đây.

Giá trị cực tiểu của hàm số đã cho là

A. -3.

B. 2.

C. 1. 

D. 0.

Câu 10. Tập nghiệm của bất phương trình ${\log }_{\frac{1}{3}}\left(x-1\right)>-2$ là

A. $\left(10;+\infty \right)$.

B. (1; 10).

C. $\left(9;+\infty \right)$.

D. $\left(-\infty ;10\right)$.

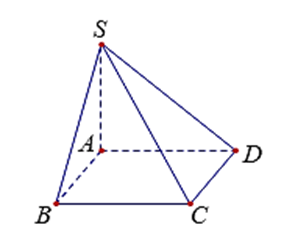
Câu 11. Cho hình chóp S.ABCD có đáy là hình bình hành. Đẳng thức nào sau đây là đẳng thức đúng?

A. $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$.

B. $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$

C. $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}+\overrightarrow{SD}$.

D. $\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{SD}$.

Câu 12. Cho A và B là hai biến cố độc lập. Biết xác suất của biến cố A là 0,4; xác suất của biến cố B là 0,3. Xác suất của biến cố A ∪ B là

A. 0,12.

B. 0,58.

C. 0,7.

D. 0,82.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)

Câu 1. Cho hàm số f(x) = 4sinx + 2x.

a) Đạo hàm của hàm số đã cho là f '(x) = -4cosx + 2.

b) f(0) = 0, f(π) = 2π

c) Nghiệm của phương trình f'(x) = 0 trên đoạn [0; π] là $\frac{2\pi }{3}$.

d) Giá trị lớn nhất của f(x) trên đoạn [0; π] là 2π + 1.

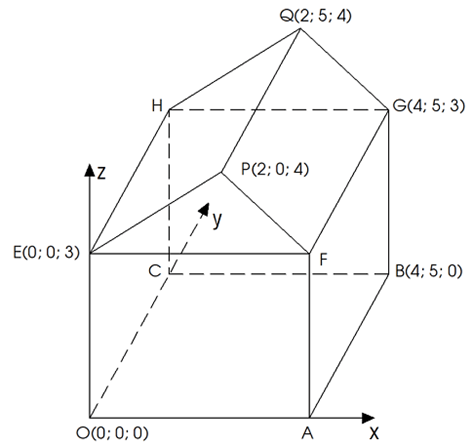
Câu 2. Hình minh họa sơ đồ một ngôi nhà trong hệ trục tọa độ Oxyz, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

a) Tọa độ điểm A là (4; 0; 0)

b) $\overrightarrow{OQ}=\left(2;5;4\right).$

c) Tọa độ $\overrightarrow{AH}=\left(4;5;3\right).$

d) C (0; 5; 0)

Câu 3. Theo báo cáo của một cơ sở sản xuất nước tinh khiết, nếu mỗi ngày cơ sở này sản xuất x (m³) nước tinh khiết thì phải trả chi phí các khoản sau: 3 triệu đồng chi phí cố định; 0,0003x² triệu đồng cho mỗi mét khối sản phẩm;  triệu đồng chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là 200 m³. Gọi C(x) là chi phí sản xuất x (m³) sản phẩm mỗi ngày và $\overline{c}\left(x\right)$ là chi phí trung bình mỗi mét khối sản phẩm.

a) $\overline{c}\left(x\right)=0,0003x+0,15+\frac{3}{x}$ .

b) C(x) = 0,0003x² + 0,15x + 5.

c) Chi phí sản xuất 100 m³ nước tinh khiết là 20 triệu đồng.

d) Chi phí trung bình mỗi mét khối sản phẩm thấp nhất khi sản lượng nước tinh khiết trong ngày là 100 m³.

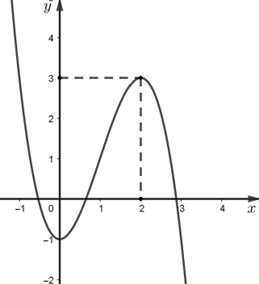
Câu 4. Cho hàm số f(x) = ax³ + bx² + cx + d có đồ thị như hình sau đây.

a) Giá trị cực tiểu của hàm số f(x) bằng -1.

b) Phương trình ${\log }_3\left(f\left(x\right)+6\right)=2$ có 2 nghiệm.

c) Hàm số f(x) đồng biến trên khoảng (1; 3).

d) Tổng 2025a + b + c+ d = -2023.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Cho hàm số $y=f\left(x\right)=\frac{2x^2+26x+18}{x+13}$ có điểm cực tiểu x = x₁ và điểm cực đại x = x₂. Tính P = -2x₁ + x₂.

Câu 2. Hai con tàu A và B đang ở cùng một vĩ tuyến và cách nhau 6 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu A chạy về hướng Nam với vận tốc 5 hải lí/ giờ, còn tàu B chạy về vị trí hiện tại của tàu A với vận tốc 7 hải lí/ giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần trăm)?

Câu 3. Cho tứ diện SABC có G là trọng tâm tam giác ABC và I là trọng tâm tam giác GBC. Biết $\overrightarrow{SI}=x\overrightarrow{SA}+y\overrightarrow{SB}+z\overrightarrow{SC}$, tính giá trị biểu thức 9(x - y + z).

Câu 4. Khảo sát thời gian tập thể dục của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau.

Thời gian (phút)	[0; 20)	[20; 420)	[40; 60)	[60; 80)	[80; 100)
Số học sinh	5	9	12	10	6

Trung bình mỗi học sinh tập bao nhiêu phút mỗi ngày? (kết quả làm tròn đến hàng phần mười).

Câu 5. Một nhóm gồm 3 học sinh lớp 10, 3 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngồi cùng vào một hàng có 9 ghế, mỗi học sinh ngồi 1 ghế. Tính xác suất để 3 học sinh lớp 10 không ngồi 3 ghế liền nhau (kết quả làm tròn đến hàng phần trăm).

Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2. Gọi M, N lần lượt là trung điểm của AB và AD. Biết hai mặt phẳng (SDM) và (SCN) cùng vuông góc với mặt phẳng (ABCD), đồng thời khoảng cách giữa DM và SC bằng $\frac{12}{7}$. Thể tích khối chóp S.ABCD bằng bao nhiêu?

-------------------Hết--------------------

BẢNG ĐÁP ÁN

PHẦN I.

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Chọn	B	C	A	A	D	D	C	D	A	B	B	B

PHẦN II.

Câu	1	2	3	4
Đáp án	a) Sai b) Đúng c) Đúng d) Sai	a) Đúng b) Đúng c) Sai d) Đúng	a) Đúng b) Sai c) Sai d) Đúng	a) Đúng b) Đúng c) Sai d) Đúng

PHẦN III.

Câu	1	2	3	4	5	6
Đáp án	4	0,57	1	51,4	0,92	8

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Cho cấp số cộng có số hạng đầu u₁ = 2, công sai d = -4. Số hạng thứ năm của cấp số cộng là

A. 512

B. -14

C. -512

D. -18

Lời giải

Ta có u₅ = u₁ + 4d = 2+ 4.(-4) = -14 .Chọn B.

Câu 2. Thống kê số phút học bài ở nhà mỗi ngày của 100 học sinh ta có bảng phân bố tần số ghép nhóm như sau

Số phút	[30; 60)	[60; 90)	[90; 120)	[120; 150)
Số học sinh	18	15	42	25

Số học sinh có thời gian học ít hơn 2 tiếng trong số học sinh trên là

A. 15

B. 33

C. 75

D. 18 . 

Lời giải

Số học sinh có thời gian học ít hơn 2 tiếng (120 phút) trong số học sinh trên là

18 + 15 + 42 = 75. Chọn C.

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; -1). Tọa độ hình chiếu vuông góc của A trên mặt phẳng (Oyz) là 

A. (0; 2; -1) .

B. (1; 0; 0).

C. (1; 2; 0) .

D. (1; 0; -1)

Lời giải

Tọa độ hình chiếu vuông góc của A trên mặt phẳng (Oyz) là (0; 2; -1) . Chọn A.

Câu 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x⁴ - 2x² - 1 trên đoạn [-1 ; 2]. Giá trị của biểu thức M + 2m bằng

A. 3.

B. 5.

C. 6.

D. 4.

Lời giải

Ta có: f'(x) = 4x³ - 4x. Xét $f^{\text{'}}\left(x\right)=0\iff \left[\begin{array}{l}x=-1\\ x=0\\ x=1\end{array}\right.$ .

Ta có f(-1) = -2; f(0) = -1; f(1) = -2; f(2) - 7.

Vậy M = 7; m = -2. Do đó M + 2m = 7 + 2.(-2) = 3. Chọn A.

Câu 5. Cho khối lăng trụ đều có diện tích đáy bằng 2 (m²) và chiều cao bằng 3 (m). Thể tích khối lăng trụ đã cho bằng

A. $\frac{3\sqrt{3}}{2}\left({\text{m}}^3\right)$.

B. 2 (m³).

C. $\frac{\sqrt{3}}{2}\left({\text{m}}^3\right)$.

D. 6 (m³)

Lời giải

Ta có: V = B.h = 2.3 = 6. Chọn D.

Câu 6. Cho hàm số f(x) liên tục trên ℝ và có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng

A. (-2; 0).

B. (-∞; 0).

C. (3; +∞).

D. (1; 3).

Lời giải

Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên khoảng (1; 3). Chọn D.

Câu 7. Đường tiệm cận xiên của đồ thị hàm số $y=2x-1+\frac{1}{x}$ có phương trình là:

A. y = 1 - 2x.

B. y = 2x.

C. y = 2x - 1.

D. y = -2x.

Lời giải

Ta thấy: $\underset{x\to +\infty }{\lim }\left[y-\left(2x-1\right)\right]=\underset{x\to +\infty }{\lim }\frac{1}{x}=0$ . Từ đó suy ra đường tiệm cận xiên của hàm số có phương trình là: y = 2x - 1. Chọn C.

Câu 8. Hàm số nào dưới đây có đồ thị như hình vẽ sau?

A. $y=\frac{x}{x+1}$.

B. $y=-\frac{x}{x-1}$.

C. $y=-\frac{x}{x+1}$.

D. $y=\frac{x}{x-1}$.

Lời giải

Đường tiệm cận đứng của đồ thị hàm số có phương trình là x = 1 nên ta loại các đáp án A, C. Đường tiệm cận ngang của đồ thị hàm số có phương trình là y = 1 nên ta loại đáp án B, chọn đáp án D. Chọn D.

Câu 9. Cho hàm số bậc ba  có đồ thị như hình vẽ dưới đây.

Giá trị cực tiểu của hàm số đã cho là

A. -3.

B. 2.

C. 1. 

D. 0.

Lời giải

Dựa vào đồ thị hàm số đã cho ta có giá trị cực tiểu của hàm số bằng -3. Chọn A.

Câu 10. Tập nghiệm của bất phương trình ${\log }_{\frac{1}{3}}\left(x-1\right)>-2$ là

A. $\left(10;+\infty \right)$.

B. (1; 10).

C. $\left(9;+\infty \right)$

D. $\left(-\infty ;10\right)$.

Lời giải

Theo giả thiết, ta có ${\log }_{\frac{1}{3}}\left(x-1\right)>-2$$\iff 0<x-1<{\left(\frac{1}{3}\right)}^{-2}$$\iff 1<x<10$ . Chọn B.

Câu 11. Cho hình chóp S.ABCD có đáy là hình bình hành. Đẳng thức nào sau đây là đẳng thức đúng?

A. $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$.

B. $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$

C. $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}+\overrightarrow{SD}$.

D. $\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{SD}$.

Lời giải

Ta có $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{BA}+\overrightarrow{SD}+\overrightarrow{DC}$$=\overrightarrow{SB}+\overrightarrow{SD}+\left(\overrightarrow{BA}+\overrightarrow{DC}\right)$$=\overrightarrow{SB}+\overrightarrow{SD}$ . Chọn B.

Câu 12. Cho A và B là hai biến cố độc lập. Biết xác suất của biến cố A là 0,4; xác suất của biến cố B là 0,3. Xác suất của biến cố A ∪ B là

A. 0,12.

B. 0,58.

C. 0,7.

D. 0,82.

Lời giải

Ta có $P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)$$=0,4\cdot 0,3=0,12$ .

Khi đó $P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)$ = 0,4 + 0,3 - 0,12 = 0,58. Chọn B.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)

Câu 1. Cho hàm số f(x) = 4sinx + 2x.

a) Đạo hàm của hàm số đã cho là f '(x) = -4cosx + 2.

b) f(0) = 0, f(π) = 2π

c) Nghiệm của phương trình f'(x) = 0 trên đoạn [0; π] là $\frac{2\pi }{3}$.

d) Giá trị lớn nhất của f(x) trên đoạn [0; π] là 2π + 1.

Lời giải

a) Sai. Ta có f '(x) = 4cosx + 2.

b) Đúng. Ta có f(0) = 4sin0 + 2.0 = 0, f(π) = 4sinπ + 2.π = 2π .

c) Đúng. $f^{\text{'}}\left(x\right)=4\cos x+2=0$$\iff \cos x=-\frac{1}{2}$$\iff x=\pm \frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$

$0\le \frac{2\pi }{3}+k2\pi \le \pi$$\iff -\frac{1}{3}\le k\le \frac{1}{6}$$\Rightarrow k=0\Rightarrow x=\frac{2\pi }{3}$

$0\le -\frac{2\pi }{3}+k2\pi \le \pi$$\iff \frac{1}{3}\le k\le \frac{5}{6}$ ⇒ không tồn tại k.

Vậy nghiệm của phương trình f'(x) = 0  trên đoạn [0; π] là $\frac{2\pi }{3}$ .

d) Sai. Ta có f(0) = 0, f(π) = 2π, $f\left(\frac{2\pi }{3}\right)=2\sqrt{3}+\frac{4\pi }{3}$

$\Rightarrow \underset{\left[0;\pi \right]}{\max }f\left(x\right)=f\left(\frac{2\pi }{3}\right)=2\sqrt{3}+\frac{4\pi }{3}$

Câu 2. Hình minh họa sơ đồ một ngôi nhà trong hệ trục tọa độ Oxyz, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

a) Tọa độ điểm A là (4; 0; 0)

b) $\overrightarrow{OQ}=\left(2;5;4\right).$

c) Tọa độ $\overrightarrow{AH}=\left(4;5;3\right).$

d) C (0; 5; 0)

Lời giải

a) Đúng. Tọa độ điểm A là (4; 0; 0)

b) Đúng. Tọa độ điểm O là (0; 0; 0) Tọa độ điểm Q là (2; 5; 4)

Do đó $\overrightarrow{OQ}=\left(2;5;4\right).$

c) Sai. Tọa độ điểm H là (0; 5; 3). Do đó tọa độ $\overrightarrow{AH}=\left(4;5;3\right).$

d) Đúng. Tọa độ điểm C là C (0; 5; 0)

Câu 3. Theo báo cáo của một cơ sở sản xuất nước tinh khiết, nếu mỗi ngày cơ sở này sản xuất x (m³) nước tinh khiết thì phải trả chi phí các khoản sau: 3 triệu đồng chi phí cố định; 0,0003x² triệu đồng cho mỗi mét khối sản phẩm;  triệu đồng chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là 200 m³. Gọi C(x) là chi phí sản xuất x (m³) sản phẩm mỗi ngày và $\overline{c}\left(x\right)$ là chi phí trung bình mỗi mét khối sản phẩm.

a) $\overline{c}\left(x\right)=0,0003x+0,15+\frac{3}{x}$ .

b) C(x) = 0,0003x² + 0,15x + 5.

c) Chi phí sản xuất 100 m³ nước tinh khiết là 20 triệu đồng.

d) Chi phí trung bình mỗi mét khối sản phẩm thấp nhất khi sản lượng nước tinh khiết trong ngày là 100 m³.

Lời giải

a) Đúng. Để sản xuất x (m³)  nước tinh khiết thì phải trả chi phí các khoản sau: 3 triệu đồng chi phí cố định; 0,15  triệu đồng cho mỗi mét khối sản phẩm; 0,0003x² triệu đồng chi phí bảo dưỡng máy móc.

Suy ra để sản xuất 1 (m³) nước tinh khiết thì cần $\frac{3}{x}$ triệu đồng chi phí cố định; 0,15 triệu đồng cho mỗi mét khối sản phẩm; 0,0003x triệu đồng chi phí bảo dưỡng máy móc.

$\Rightarrow \overline{c}\left(x\right)=\frac{3}{x}+0,15+0,0003x$ (triệu đồng).

b) Sai. Khi đó, ta suy ra $C\left(x\right)=\overline{c}\left(x\right)\cdot x$ $=3+0,15x+0,0003x^2$.

c) Sai. Chi phí sản xuất 100 m³ là C(100) = 3 + 0,15.100 + 0,0003.100² = 21 (triệu đồng).

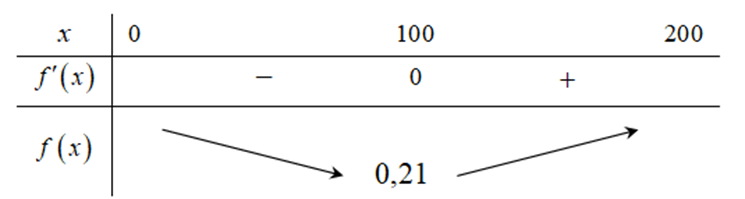
d)Đúng. Hàm chi phí trung bình mỗi mét khối sản phẩm là  $\overline{c}\left(x\right)=\frac{3}{x}+0,15+0,0003x$,$0<x\le 200$ .

Đặt $f\left(x\right)=\overline{c}\left(x\right)=\frac{3}{x}+0,15+0,0003x$, $0<x\le 200$ .

$f^{\text{'}}\left(x\right)=-\frac{3}{x^2}+0,0003$.

$f^{\text{'}}\left(x\right)=0$$\Rightarrow -3+0,0003x^2=0$$\Rightarrow x=100$

Bảng biến thiên của hàm f(x).

Dựa vào BBT thì chi phí trung bình mỗi mét khối sản phẩm thấp nhất khi sản lượng nước tinh khiết trong ngày là 100 m³.

Câu 4. Cho hàm số f(x) = ax³ + bx² + cx + d có đồ thị như hình sau đây.

a) Giá trị cực tiểu của hàm số f(x) bằng -1.

b) Phương trình ${\log }_3\left(f\left(x\right)+6\right)=2$ có 2 nghiệm.

c) Hàm số f(x) đồng biến trên khoảng (1; 3).

d) Tổng 2025a + b + c+ d = -2023.

Lời giải

a)Đúng. Dựa vào đồ thị hàm số ta thấy giá trị cực tiểu của hàm số f(x) bằng -1

b)Đúng. Ta có: ${\log }_3\left(f\left(x\right)+6\right)=2$$\iff f\left(x\right)+6=9$$\iff f\left(x\right)=3$ (*)

Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f(x)  với đường thẳng y = 3. Dựa vào đồ thị ta thấy phương trình (*) có 2 nghiệm.

c)Sai. Dựa vào đồ thị ta thấy hàm số y = f(x) đồng biến trên khoảng (1; 2) và nghịch biến trên khoảng (2; 3).

d)Đúng. Ta có f(x) = 3ax² + 2bx + c.

Theo giả thiết ta có: $\left\{\begin{array}{l}{f}^{\text{'}}\left(0\right)=0\\ f^{\text{'}}\left(2\right)=0\\ f\left(0\right)=-1\\ f\left(2\right)=3\end{array}\right.$$\iff \left\{\begin{array}{l}c=0\\ 12a+4b+c=0\\ d=-1\\ 8a+4b+2c+d=3\end{array}\right.$$\iff \left\{\begin{array}{l}a=-1\\ b=3\\ c=0\\ d=-1\end{array}\right.$ .

Tổng 2025a + b + c+ d = -2025 + 3 + 0 -1 = -2023

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Cho hàm số $y=f\left(x\right)=\frac{2x^2+26x+18}{x+13}$ có điểm cực tiểu x = x₁ và điểm cực đại x = x₂. Tính P = -2x₁ + x₂.

Lời giải

Ta có $y^{\text{'}}=f^{\text{'}}\left(x\right)$$=\frac{\left(4x+26\right)\left(x+13\right)-\left(2x^2+26x+18\right)}{{\left(x+13\right)}^2}$$=\frac{2x^2+52x+320}{{\left(x+13\right)}^2}$

$y^{\text{'}}=0\iff 2x^2+52x+320=0$$\iff \left[\begin{array}{l}x=-16\\ x=-10\end{array}\right.$

Hàm số đạt cực tiểu tại x = x₁ = -10 và đạt cực đại tại x = x₂ = -16.

Khi đó P = -2x₁ + x₂ = -2.(-10) - 16 = 4

Đáp án: 4.

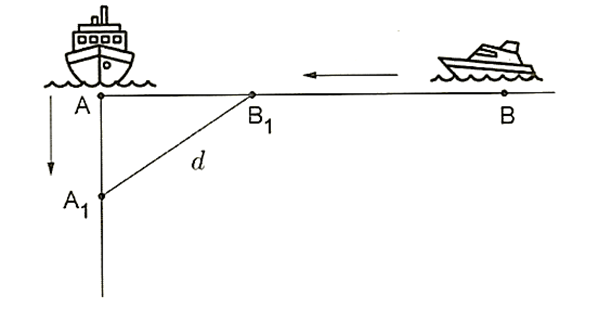
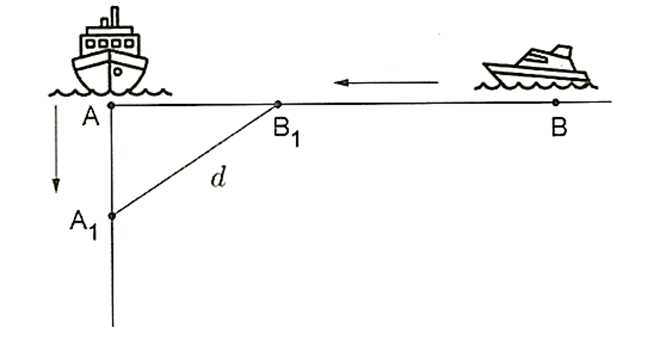
Câu 2. Hai con tàu A và B đang ở cùng một vĩ tuyến và cách nhau 6 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu A chạy về hướng Nam với vận tốc 5 hải lí/ giờ, còn tàu B chạy về vị trí hiện tại của tàu A với vận tốc 7 hải lí/ giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần trăm)?

Lời giải

Giả sử ban đầu tàu A ở vị trí A và tàu B ở vị trí B. Sau khoảng thời gian t:

Tàu A di chuyển được quãng đường 5t về phía Nam đến vị trí A₁.

Tàu B di chuyển được quãng đường 7t đến vị trí B₁.

Khoảng cách từ vị trí B₁  đến vị trí A là 6 = 7t.

Áp dụng định lý Pytago ta có: 

$d=A_1{B}_1=f\left(t\right)$$=\sqrt{{\left(6-7t\right)}^2+{\left(5t\right)}^2}$$=\sqrt{74t^2-84t+36}$

Để khoảng cách giữa hai tàu nhỏ nhất, thì hàm số $g\left(t\right)=74t^2-84t+36$ đạt giá trị nhỏ nhất.

Hàm số g(t) đạt giá trị nhỏ nhất tại $t=\frac{-\left(-84\right)}{2.74}=\frac{21}{37}$, vậy thời điểm khoảng cách giữa hai tàu bé nhất là khi $t=\frac{21}{37}\approx 0,57$ (giờ).

Đáp án: 0,57.

Câu 3. Cho tứ diện SABC có G là trọng tâm tam giác ABC và I là trọng tâm tam giác GBC. Biết $\overrightarrow{SI}=x\overrightarrow{SA}+y\overrightarrow{SB}+z\overrightarrow{SC}$, tính giá trị biểu thức 9(x - y + z).

Lời giải

Do I là trọng tâm tam giác GBC nên ta có: $\overrightarrow{SI}=\frac{1}{3}\left(\overrightarrow{SG}+\overrightarrow{SB}+\overrightarrow{SC}\right)\left(1\right)$

Do G là trọng tâm tam giác ABC nên ta có:  $\overrightarrow{SG}=\frac{1}{3}\left(\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}\right)\left(2\right)$

Thay (2) vào (1) ta có: 

$\overrightarrow{SI}=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}\right)+\overrightarrow{SB}+\overrightarrow{SC}\right)$$=\frac{1}{9}\overrightarrow{SA}+\frac{4}{9}\overrightarrow{SB}+\frac{4}{9}\overrightarrow{SC}$

Vậy $\left\{\begin{array}{l}x=\frac{1}{9}\\ y=\frac{4}{9}\\ z=\frac{4}{9}\end{array}\right.\Rightarrow 9\left(x-y+z\right)=1$

Đáp án: 1.

Câu 4. Khảo sát thời gian tập thể dục của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau.

Thời gian (phút)	[0; 20)	[20; 420)	[40; 60)	[60; 80)	[80; 100)
Số học sinh	5	9	12	10	6

Trung bình mỗi học sinh tập bao nhiêu phút mỗi ngày? (kết quả làm tròn đến hàng phần mười).

Lời giải

Gọi $x_1=10;$$x_2=30;$$x_3=50;$$x_4=70;$$x_5=90$ là các giá trị đại diện.

Khi đó $\overline{x}=\frac{10\cdot 5+30\cdot 9+50\cdot 12+70\cdot 10+90\cdot 6}{42}$$\approx 51,4$ phút.

Đáp án: 51,4.

Câu 5. Một nhóm gồm 3 học sinh lớp 10, 3 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngồi cùng vào một hàng có 9 ghế, mỗi học sinh ngồi 1 ghế. Tính xác suất để 3 học sinh lớp 10 không ngồi 3 ghế liền nhau (kết quả làm tròn đến hàng phần trăm).

Lời giải

Ta có $n\left(\Omega \right)=9!$

Gọi A là biến cố: “xếp được 3 học sinh lớp 10 ngồi 3 ghế liền nhau”.

Khi đó, $n\left(A\right)=7!\cdot 3!$. Suy ra $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{3!\cdot 7!}{9!}=\frac{1}{12}$

Vậy xác suất để 3 học sinh lớp 10 không ngồi 3 ghế liền nhau là $P\left(\overline{A}\right)=1-P\left(A\right)=\frac{11}{12}\approx 0,92$

Đáp án: 0,92.

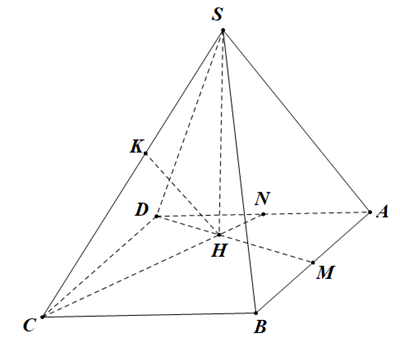
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2. Gọi M, N lần lượt là trung điểm của AB và AD. Biết hai mặt phẳng (SDM) và (SCN) cùng vuông góc với mặt phẳng (ABCD), đồng thời khoảng cách giữa DM và SC bằng $\frac{12}{7}$. Thể tích khối chóp S.ABCD bằng bao nhiêu?

Lời giải

Gọi $H=DM\cap CN$

Theo bài ra ta có $SH\perp \left(ABCD\right)$

Do $\Delta ADM=\Delta DCN\left(\text{c.g.c}\right)$ nên $\widehat{AMD}=\widehat{DNC}$

$\widehat{HDN}+\widehat{DNH}=\widehat{HDN}+\widehat{AMD}=90°$(Do tam giác vuông tại ).

Nên $DM\perp CN$

Ta có $DM\perp SH,DM\perp CN$$\Rightarrow DM\perp \left(SCN\right)$

Trong mặt phẳng (SCN), kẻ $HK\perp SC\left(K\in SC\right)$

Do $\left\{\begin{array}{l}DM\perp \left(SCN\right)\\ KH\subset \left(SCN\right)\end{array}\right.\Rightarrow KH\perp DM$

Nên KH là đường vuông góc chung của DM và SC.

Khi đó $d\left(SC,MD\right)=HK=\frac{12}{7}$

Ta có tam giác CDN vuông tại D nên $CN=\sqrt{C{D}^2+D{N}^2}=\sqrt{4+1}=\sqrt{5}$

Áp dụng hệ thức lượng trong tam giác vuông CDN có: $C{D}^2=CN\cdot CH\Rightarrow CH=\frac{4}{\sqrt{5}}$

Trong tam giác vuông SHC có: $\frac{1}{H{K}^2}=\frac{1}{S{H}^2}+\frac{1}{C{H}^2}$$\Rightarrow \frac{1}{S{H}^2}=\frac{49}{144}-\frac{5}{16}=\frac{1}{36}$$\Rightarrow SH=6$

Vậy $V_{S.ABCD}=\frac{1}{3}\cdot SH\cdot S_{ABCD}$$=\frac{1}{3}\cdot 6\cdot 2^2=8.$

Đáp án: 8.

................................

................................

................................

Trên đây tóm tắt một số nội dung miễn phí trong bộ đề thi khảo sát chất lượng đầu năm Toán 12 năm 2025 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử

Xem thêm đề thi KSCL đầu năm các môn học có đáp án hay khác:

• Đề thi khảo sát chất lượng đầu năm Ngữ Văn 6 (10 đề)
• Đề thi khảo sát chất lượng đầu năm Văn 7 (10 đề)
• Đề Khảo sát chất lượng đầu năm Văn 8 (5 đề)
• Đề thi khảo sát chất lượng đầu năm Toán lớp 2 (6 đề)
• Đề thi khảo sát chất lượng đầu năm Toán lớp 3
• Đề thi khảo sát chất lượng đầu năm Toán 6 (5 đề)
• Đề thi khảo sát chất lượng đầu năm Toán 7 (3 đề)
• Đề thi khảo sát chất lượng đầu năm Toán 8 (3 đề)
• Đề thi khảo sát chất lượng đầu năm Toán 10 (3 đề)
• Đề thi khảo sát chất lượng đầu năm Toán 11 (3 đề)

Xem thêm đề thi lớp 12 các môn học có đáp án hay khác:

Đề ôn thi Tốt nghiệp (các môn học), ĐGNL, ĐGTD các trường có đáp án hay khác:

Tài liệu giáo án lớp 12 các môn học chuẩn khác:

Để học tốt lớp 12 các môn học sách mới:

• Giải bài tập Lớp 12 Kết nối tri thức
• Giải bài tập Lớp 12 Chân trời sáng tạo
• Giải bài tập Lớp 12 Cánh diều

---